N体问题下日地三角拉格朗日点的数值研究

刘媛琪，周珊羽，巩子嘉

(1.山东大学(威海) 空间科学与物理学院/空间科学研究院，山东 威海 264209；2.山东大学(威海) 数学与统计学院，山东 威海 264209)



N体问题下日地三角拉格朗日点的数值研究

刘媛琪1，周珊羽1，巩子嘉2

(1.山东大学(威海) 空间科学与物理学院/空间科学研究院，山东 威海 264209；2.山东大学(威海) 数学与统计学院，山东 威海 264209)

针对日地系统的拉格朗日点相关的N体问题(N>3)目前尚无可用的解析理论解的问题，试图通过数值方法，运用摄动理论的思想，得出限制性三体问题下的日地三角拉格朗日点(L4、L5)在N体问题下的引力值(非零引力合力偏差)。通过对拉格朗日点的摄动规律进行定性和定量分析，从来源、周期性等方面总结分析，为深空探测相关研究提供参考。

拉格朗日点；N体问题；数值方法

0 引言

1772年，意大利科学家拉格朗日推导出2个质量相差悬殊的天体在同一平面上存在5个特殊的点，在这5个点上物体所受到的引力与物体运动产生的向心力达到平衡，这5个点也被称为“拉格朗日点”(记为L1～L5)(如图1所示)。

从图中可知，L4、L5点在距离太阳和地球相等距离的2个等边三角形顶点处，所以也称为三角拉格朗日点。众所周知，三角形结构具有稳定性，科学家在1906年发现第617号小行星出现在木星轨道落后60°处；20世纪80年代，科学家又发现在土星和它的大卫星所构成的运动系统中也有类似的等边三角形。数学的推导和天文观测结论证明了拉格朗日点的特殊性确实存在。

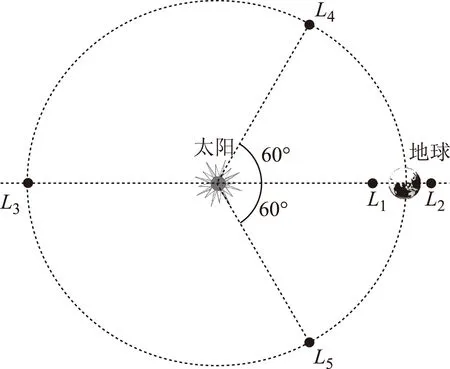
图1 日地三体系统的拉格朗日点

日地拉格朗日点因与太阳和地球相对位置的不变性而成为国际空间探测的热点。在拉格朗日点上，航天器可以基本保持稳定的轨道而不消耗太多燃料来维持；因此拉格朗日点也是公认的望远镜和探测器的绝佳位置以及未来太空城的最佳位置。目前，威尔金森微波背景各向异性探测器已经在日-地系统的L2点上运行，詹姆斯韦伯太空望远镜将要被放置在日-地系统的L2点上。我国的嫦娥二号在各项科学目标都取得圆满成功后开始了新的征程，奔向150万km外的拉格朗日L2点。2011-08-25 T 23：27：00，经过77 d的飞行，嫦娥二号在世界上首次实现从月球轨道出发，受控准确进入日-地系统的L2点环绕轨道，第一次实现中国对月球以外的太空进行探测，是中国第一次开展拉格朗日点转移轨道和使命轨道的设计和控制，并实现了150万km远距离测控通信。

在天体力学中，行星系统的起源和演化问题一直是大家关注的重点。对这类问题，需要解N体运动的微分方程；但这些方程一般都相当复杂，除了二体问题等几种少数情况外，都不能得到严格的分析解。目前常用的研究方法是摄动理论，先用二体问题近似，然后再进一步考虑摄动因素影响。如为了得到精确的行星轨道，除了考虑太阳的影响，还要考虑太阳系中其他行星的引力作用，尤其是木星这样的大质量行星对其他行星产生的影响。现代精密的天体测量技术已经可以测定出对于二体运动非常微小的偏离。

至今为止对日地系统三体限制性拉格朗日点的研究做了近似，尤其是忽略了其他天体的影响、将所有运动轨道都近似看作在黄道面上。本文考虑了黄道坐标系三维空间内8大行星在拉格朗日点的引力作用，以期得到限制性三体问题下日地拉格朗日点在太阳系内受行星影响的情况。

本文利用开普勒根数计算给定时间黄道坐标系内8大行星的精确位置。假设太阳和地球对拉格朗日点的引力和与其向心力完全相同，其他行星在拉格朗日点的加速度通过最基础的加速度矢量叠加，即可求解拉格朗日点受到影响(数值)的规律。

通过研究发现，在黄道坐标系内，金星对拉格朗日点z方向上有一定周期性的扰动，与金星距离地球较近且有3°的轨道倾角情况相符。同时，在黄道面内，拉格朗日点受木星扰动最大，且有一定的周期性规律，与木星距离地球近且质量较大的情况相符。

通过摄动理论，可以解决许多天文学与空间科学中的重要问题，例如证明太阳系存在的第九大行星、深空探测卫星轨道设计等。如能够通过数值方法将摄动理论充分应用，将对摄动理论的发展产生重要的影响。

1 计算过程

1.1 确定8大行星在给定日期的状态矢量

其步骤如下：

1)求儒略日JD[2]203-208。

根据儒略日的定义，用下式推算某日世界时0时刻的儒略日

(1)

式中：y为年份；m为月份；d为天数；int表示取整运算符。

2)求J2000至给定日期的儒略世纪T0。

J2000表示儒略纪元法，本文中所用轨道根数均在儒略纪元2000时为起始值，并有世纪变化率。因此在计算时需得出J2000至给定日期的儒略世纪

(2)

3)求得轨道根数在T0时的值

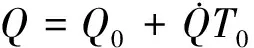
(3)

4)求JD时的近日点幅角ω、真近点角θ[2]155-161。

ω=ϖ-Ω

M=L-ϖ，

(4)

式中：ϖ为近日点纬度；Ω为升交点赤经；M为平近点角。

开普勒方程为

M=E-e sinE。

(5)

式中：E为偏近点角；e为椭圆轨道偏心率。

可以通过迭代逼近求得偏近点角E为

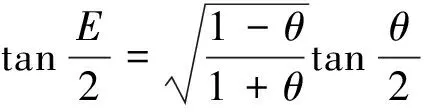
(6)

即可求得真近点角θ。

5)由轨道根数求解状态矢量R、v[1]224-228，[2]203-208。

①轨道面坐标系下(以行星各自轨道面为z轴，轨道焦点为原点)有

(7)

式中a为椭圆轨道半长轴。

②转换为日心黄道坐标系的变换矩阵为

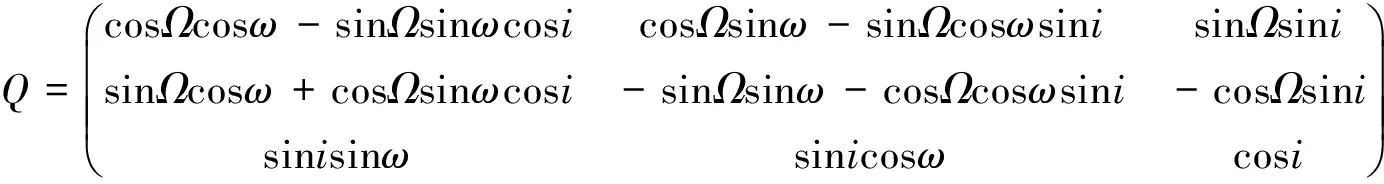
(8)

式中：Ω为升交点赤经；ω为近日点幅角；i为轨道倾角。则

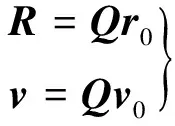
(9)

1.2 L4、L5拉格朗日点的精确轨道

1)拉格朗日点L4：L4点在以限制性3体问题的2个主天体(本文中均在日地系统中进行研究，分别指太阳和地球)连线为底边的等边三角形的第3个顶点上，在较小天体围绕2天体系统质心运行轨道的前方，则

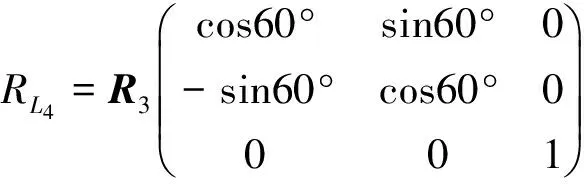
(10)

式中：R代表日心黄道坐标系内位置参量；下标L4代表拉格朗日4点上测试质量的位置参量；下标3代表地球。由于L4点的轨道也在地球公转平面上，因此在黄道坐标系的xOy平面上可通过地球状态参量旋转得到其状态参量。

2)拉格朗日点L5：L5点在以2个主天体连线为底边的等边三角形的第3个顶点上，在较小天体围绕2天体系统质心运行轨道的后方。则有

(11)

式中下标L5代表拉格朗日5点上测试质量的位置参量。由于L5点的轨道也在地球公转平面上，因此在黄道坐标系的xOy平面上可通过地球状态参量旋转得到其状态参量。

1.3 计算拉格朗日点受其他行星运行的影响

1)目标函数(向量)

(12)

式中：F为拉格朗日点轨道上实验质量m受到的万有引力合力矢量；下标N-body代表N体问题条件下，3-body代表三体问题条件下。

2)三体问题下

(13)

式中:G为万有引力常数G=6.67×10-11·m3·kg-1·s-2;M为天体质量；下标0为太阳；1～8依次代表由近及远的太阳系8大行星。方程右边由万有引力定律得出。

3)N体问题下

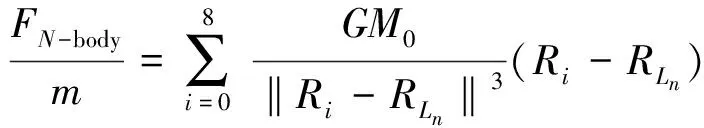
(14)

4)目标函数

(15)

目标函数是N体问题和三体问题万有引力合力的差值，也就是三体问题下拉格朗日点受到行星的摄动力影响。

2 数值分析

2.1 L4点的受力分析

图2所示为L4点所受太阳及8大行星加速度之和大小(标量)的变化，横轴单位为d(指经过2015-01-01 T 00∶00∶00的天数，下文如无特别指出均为此含义)，纵轴单位为10-5m·s-2。取若干点对日地合加速度和其余行星合加速度数量级进行计算，均有近10个数量级之差。由此可见，拉格朗日点受8大行星摄动影响较为有限，基本处于十分稳定的状态；但合加速度变化幅度有一定的周期性，可以进行进一步研究。

图2 太阳及太阳系8大行星在L4的合加速度

图3分别为除金星、木星和地球外5个行星(小图题目所示)在拉格朗日L4点的摄动加速度大小的三维分布(深色)与L4点所受太阳及8大行星合加速度大小的三维分布(浅色)的对比图。如图3所示，以上5个行星的加速度比合加速度小至少1个数量级，如此微小的摄动可以忽略不计。

图3 行星在L4引力加速度与合加速度比较图

图4中深色线为金星在L4点的加速度在10 000 d内的轨迹图。不难看出金星在L4点的引力作用产生的加速度与合加速度(浅色)的z分量周期性变化规律及极值大小几乎相同。金星与地球距离较小，且具有3.4°的轨道倾角，相比其他行星，认为其倾角足够大而足以产生较为明显的影响；所以不难理解L4点在z方向的摄动主要是受金星位置的影响。而且由于金星周期比地球周期小;所以z方向加速度的周期性变化十分明显，峰值往往出现在金星近地点。接下来对其变化周期与极值点出现时金星与L4点的相对位置进行分析讨论。

图5为木星对L4点引力作用产生加速度与合加速度在10 000 d内的变化轨道图。深色线为木星在L4点的加速度，与合加速度(浅色)在xOy平面分量非常接近。木星是距离地球最大的巨行星，轨道倾角1.3°，其对拉格朗日点在黄道面上的影响最大也是可以合理解释的。虽然木星周期较大，但拉格朗日点的轨道周期与地球相同;所以其共线的周期在10 000 d内有多次的体现。

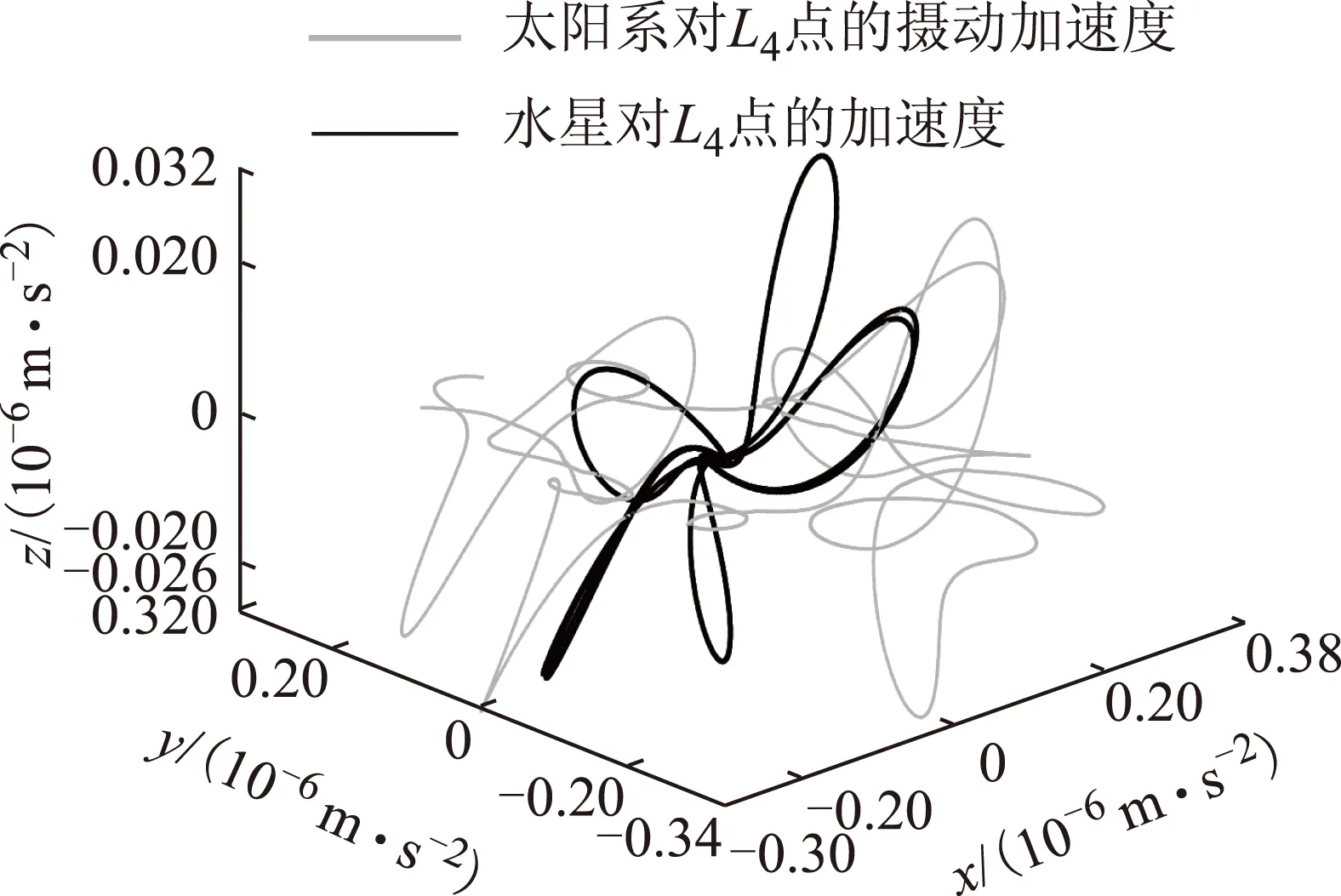
图4 金星在L4引力加速度与合加速度比较图

图5 木星在L4引力加速度与合加速度比较图

图6为L4点处金星万有引力在10 000 d内随时间的变化。图7为L4点处木星万有引力随时间的变化。与金星在L4点引力的极大值变化规律略有不同，木星在L4点引力作用产生的加速度极大值有明显的浮动，这与木星轨道与地球轨道相比离心率较大(是地球的2.8倍)，同时半长轴较大(是地球的5倍)有关，与金星更近似为正圆(离心率是木星的1/8)的轨道差别较大。

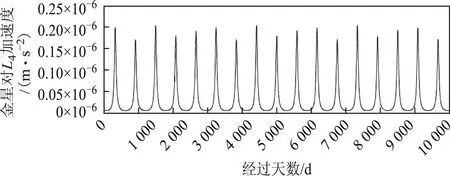
图6 金星在L4引力加速度标量变化图

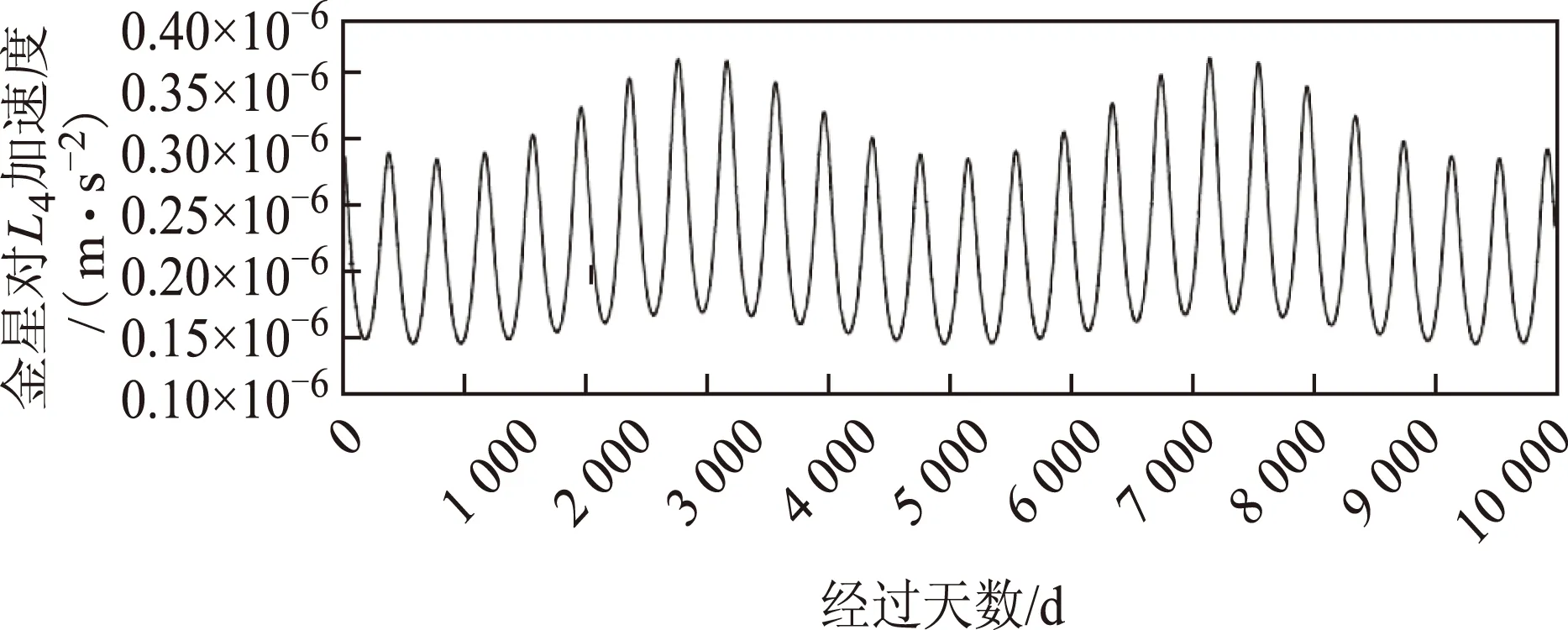
图7 木星在L4引力加速度标量变化图

根据以上分析可以看出，拉格朗日点摄动影响有明显的周期性规律，既有长周期，又有短周期，且与三角函数等形式较为接近；因此通过时间序列谱分析可以提取其中隐含的部分信息并直观理解其原因。本文选取木星在L4点引力加速度随时间的变化作为示例。

通过离散傅里叶变换(discrete Fourier transform，DFT)把原始序列信号从时间域变换到频率域，即把原始序列x(n)映射成新的序列

k=0,1,2,…,N-1。

(16)

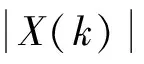
设第k个点对应频率是fk，则

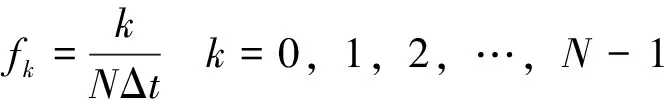
(17)

式中NΔt是原始点列x(n)中相邻2个点横坐标的间隔，即采样周期。

在对木星在L4点引力加速度随时间的变化进行分析时，取Δt=10，点数N=10 000，经过离散傅里叶变换，得到频谱图如图8所示。

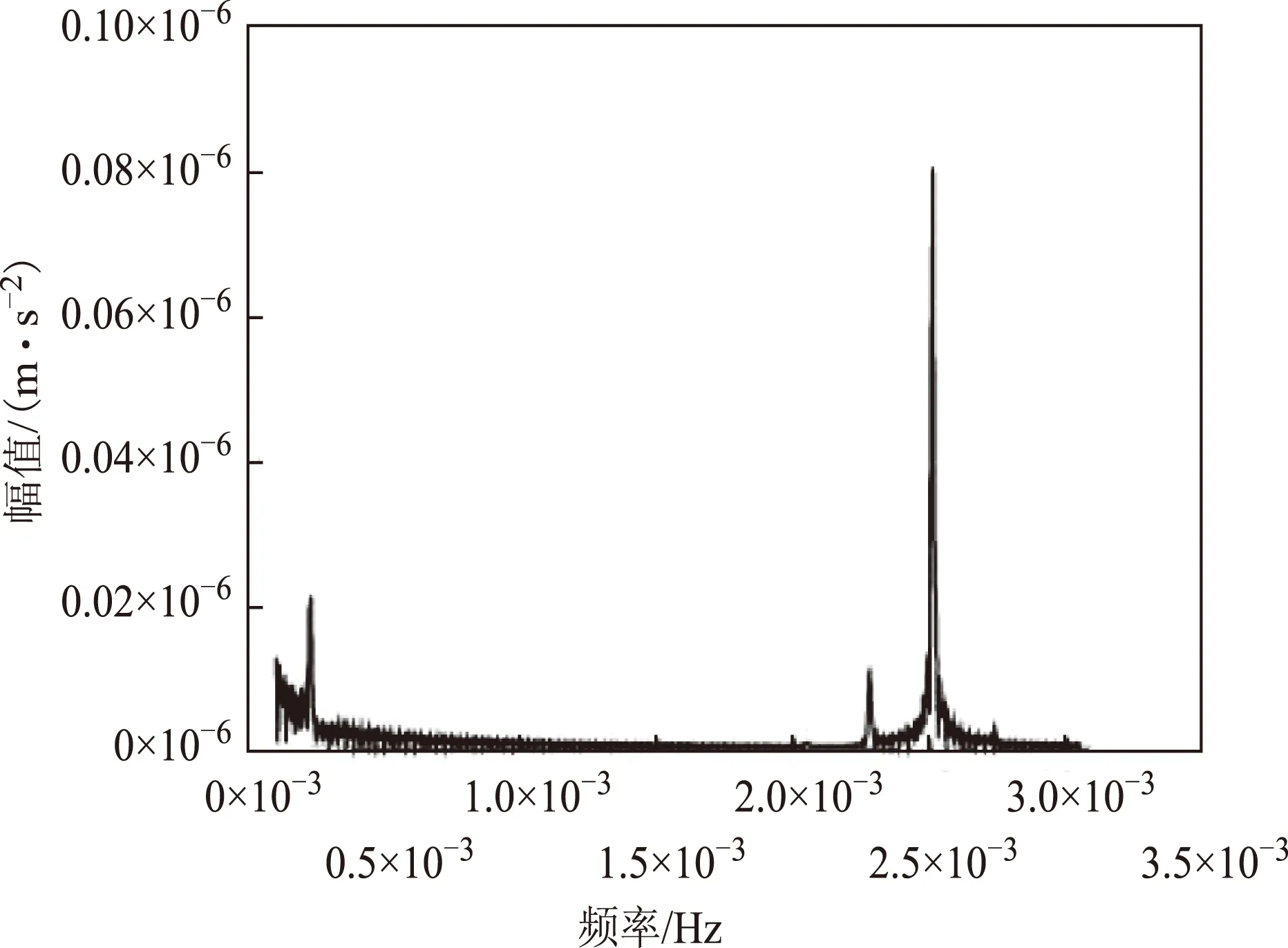
图8 木星在L4引力加速度变化频谱图

由频谱图可以看出，振幅出现峰值的3个频率从小到大依次是

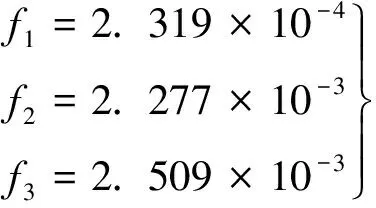
(18)

其对应周期分别是

(19)

式中:T1与木星的公转周期接近；T3与木星、地球的相遇周期接近，与将天体运动看作匀速圆周运动近似计算的两行星相遇周期400 d几乎一致。

根据直观分析我们认为所分析周期可以看作是三角函数形式的周期(将离散的点看作连续函数a=a(t)，所以假设函数是由3个余弦函数相加而成，即

a(t)=a0+∑Ricos(2πfit) i=1,2,3。

(20)

式中3个频率是通过频谱中的峰值频率得到的。

利用最小二乘法拟合对点列x(n)做线性回归，求出系数a=a0、Ri，其结果如图9所示。

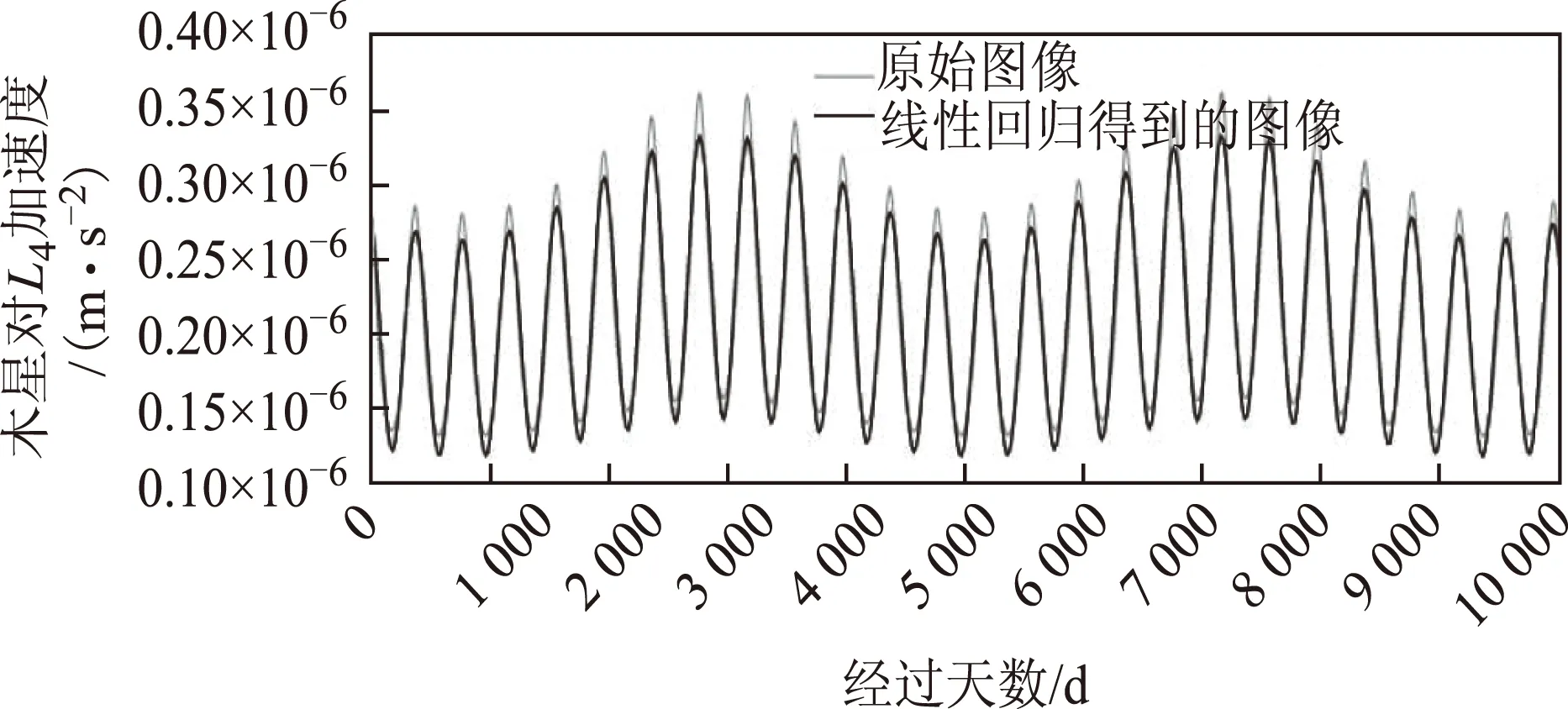
图9 木星在L4引力加速度周期性变化与线性拟合函数对比图

深色线表示的拟合曲线与浅色的原曲线相比图像拟合十分理想，长短周期都基本吻合，在相位上也无较大误差。因此，数值分析可以大致认为摄动的周期性基本由拉格朗日点公转周期和引起摄动的行星公转周期决定。

2.2 L5点的受力分析图示

L5点在受力方面与L4点的结果非常相似，互相验证。这里只将结果展示在图10～图14中以供参考。

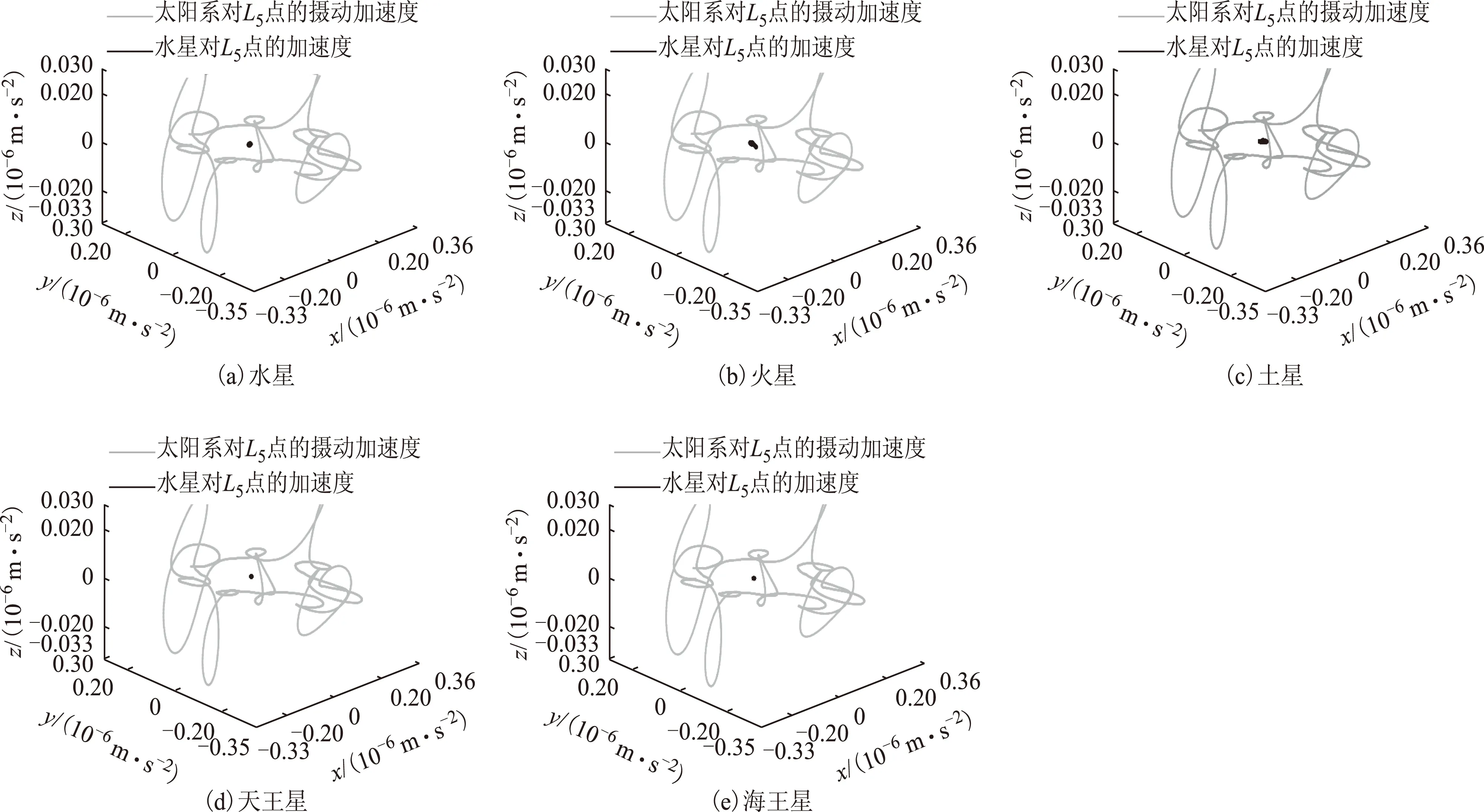
图10 行星在L5引力加速度与合加速度比较图

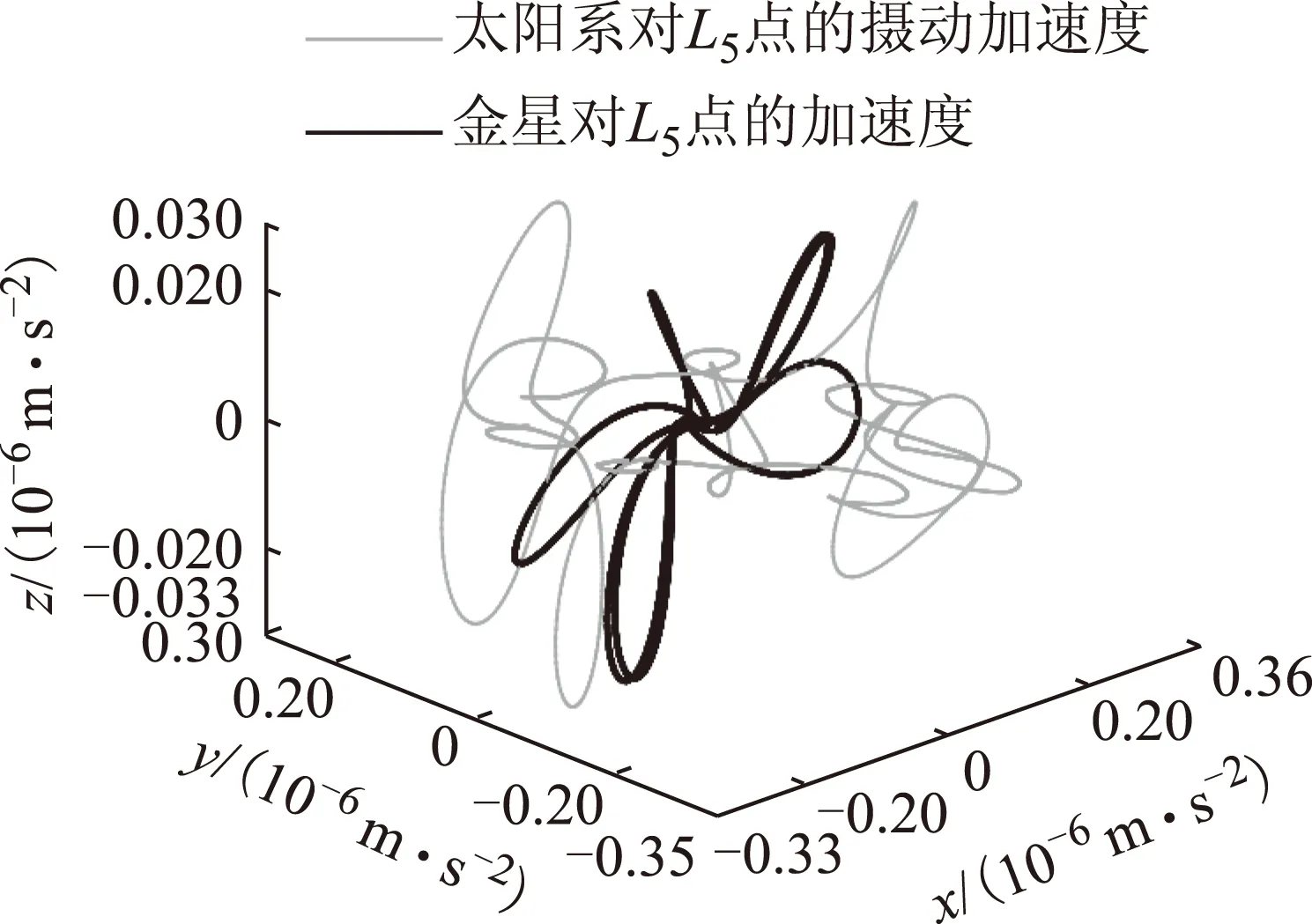
图11 金星在L5引力加速度与加速度比较图

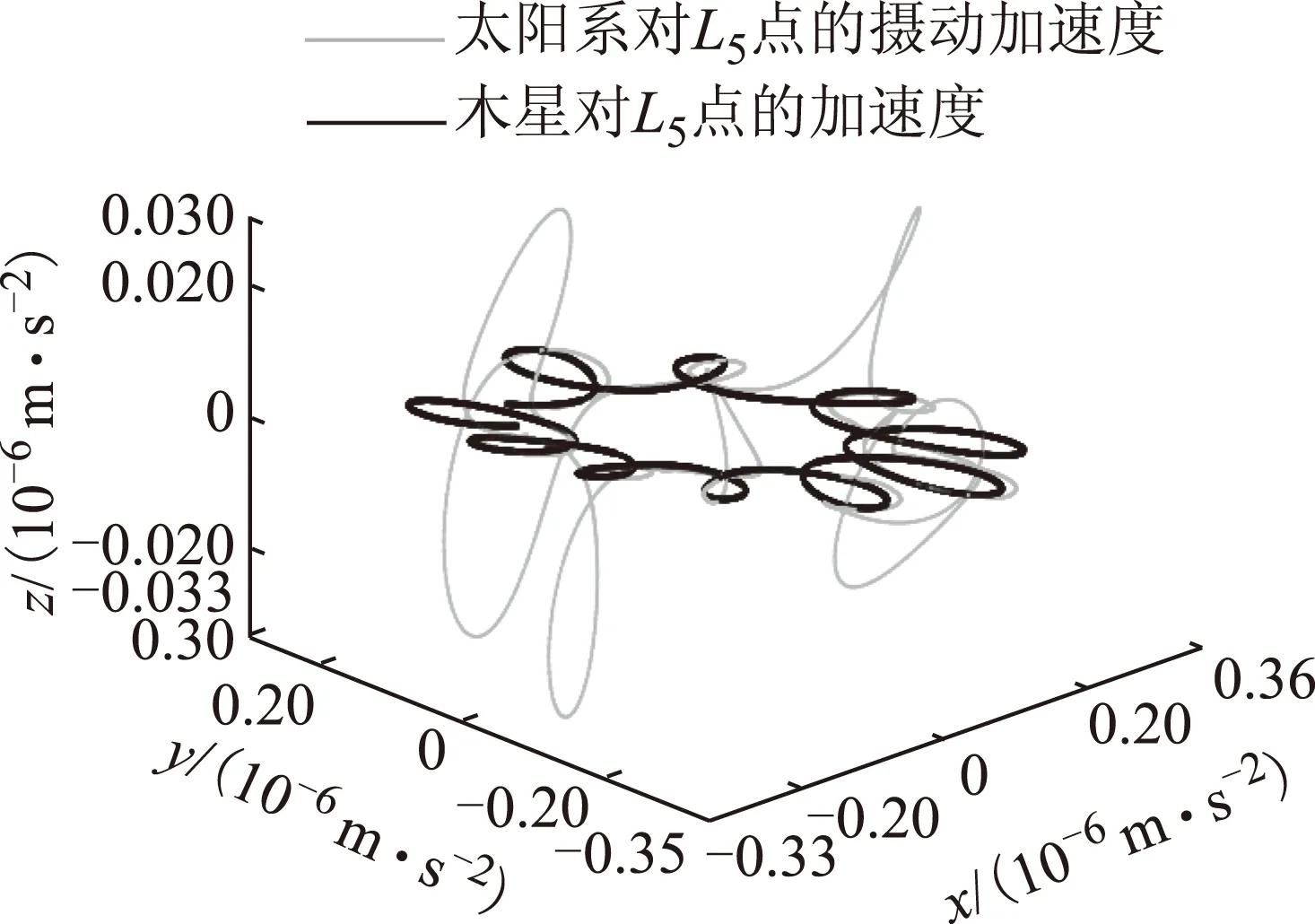
图12 木星在L5引力加速度与合加速度比较图

图13 金星在L5引力加速度标量变化图

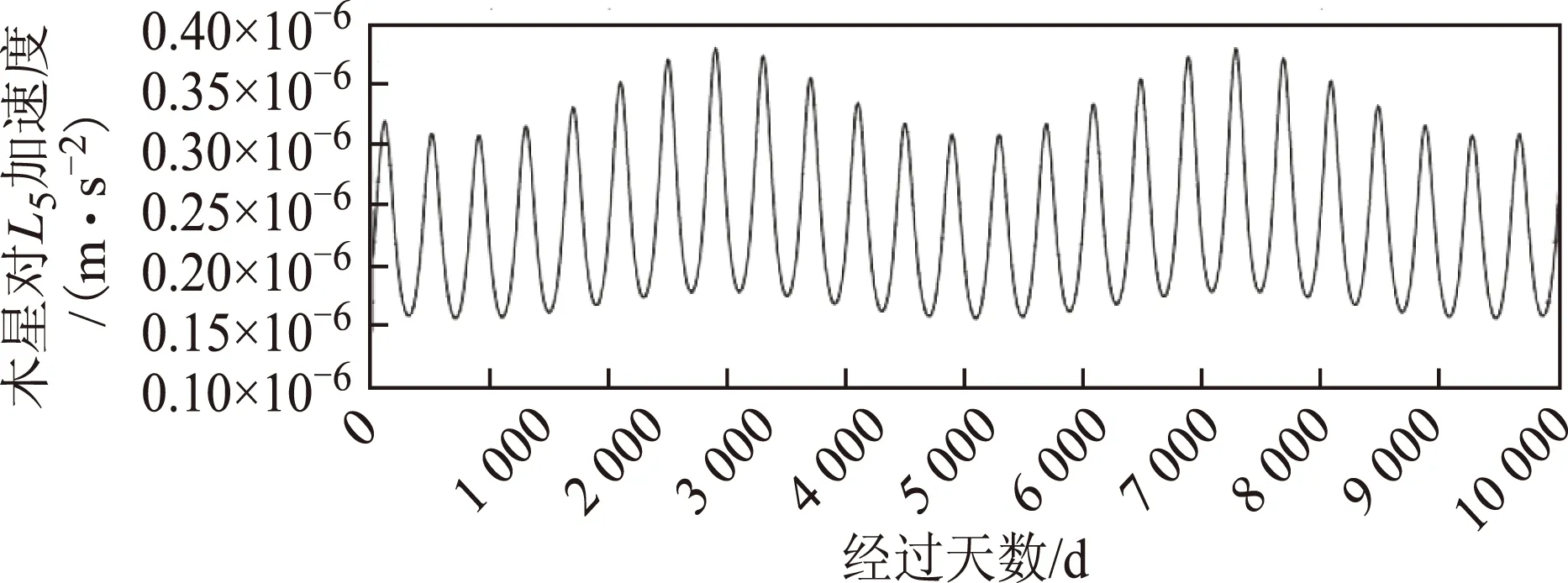
图14 木星在L5引力加速度标量变化图

3 结果检验

根据L4、L5点的分析结果，选取几个特殊的点分析了极值点出现时有特别特征的天体金星与拉格朗日点的相对位置。图15为1 050 d内金星与三角拉格朗日点的轨道图。

图15 引力作用极值时位置示意图

图中深色线是金星的运行轨道，浅色线为三角拉格朗日点的轨道(与地球轨道完全相同)；选取1 495 dL4点与金星的相对位置(深色圆点)与717 dL5点与金星的相对位置(浅色圆点)作为示例，2个时间点天体与拉格朗日点的位置是在周期内达到最近：以此验证我们以上的分析是符合科学原理与常识的。

4 结束语

本文对N体问题的下拉格朗日点进行定性和定量分析，从时间域、空间域、频率域中找寻规律。通过研究发现，三角拉格朗日点在N体问题中(考虑8大行星)受到的摄动非常有限，与向心加速度相差在10个数量级左右。同时可以得出在黄道坐标系内，金星对拉格朗日点z方向上有一定周期性的扰动，与金星距离地球较近且有3°的轨道倾角情况相符。在黄道面内拉格朗日点受木星扰动最大，且有一定的周期性规律，与木星质量较大的情况相符。摄动加速度的周期性与行星公转周期有密切关系，尤其是拉格朗日点与行星相遇周期有一定的复合规律。

致谢：感谢许国昌教授、山东大学空间科学研究院导航与遥感实验室杜玉军等各位老师、师兄师姐和朋友们对本文的指导。

[1] XU G C，XU J.Orbits[M].Berlin：Springer Berlin，2013：103-120.

[2] CURTIS H D.Orbital mechanics for engineering students[M].3rd ed.Oxford：Butterworth-Heinemann Elsevier Ltd，2014.

[3] MURALIDHAR K，SARATHY R.A theoretical basis for perturbation methods[J].Statistics & Computing，2003，13(4)：329-335.

[4] 李广宇.天体测量和天体力学基础[M].北京：科学出版社，2015.

[5] 孙义燧.现代天体力学导论[M].高等教育出版社，2008.

[6] 李广侠，姜勇，孙玉华.拉格朗日点在深空通信中的应用[J].数字通信世界，2011(1)：84-87.

[7] 张宁博，乔栋.拉格朗日点观测与探测任务发展现状与分析[C]//中国宇航学会深空探测技术专业委员会.中国宇航学会深空探测技术专业委员会第八届学术年会论文集(下篇).上海：中国宇航学会深空探测技术专业委员，2011：497-505.

[8] 林辉庆.拉格朗日L-4点的理论验算[J].物理教师，2012，33(4)：42-43.

[9] 胡先进，李力.简明推导“三角拉格朗日点”的新方法[J].物理教师，2013，34(5)：54-55.

[10]张文昭，刘文忠，孙艳春，等.N体问题中心构型的数学定义[J].北京师范大学学报：自然科学版，2011，47(4)：359-361.

[11]刘文中，张同杰.N体问题共线解的简明数值方法[J].北京师范大学学报：自然科学版，2005，41(1)：54-57.

[12]杨远玲，聂清香，吴晓梅，等.N体问题的几种数值算法比较[J].计算物理，2006，23(5)：599-603.

Numerical study on Sun-Earth Lagrangian points of N-body problem

LIU Yuanqi1，ZHOU Shanyu1，GONG Zijia2

(1.School of Space Science and Physics/Institute of Space Science，Shandong University，Weihai，Shandong 264209，China；2.School of Mathematics and Statistics，Shandong University(Weihai)，Weihai，Shandong 264209，China )

Aiming at the problem that theN-body problem (N>3) has no analytical solution in the related existed study on Lagrangian points in Sun-Earth system，the paper tried to establish a 3D model to describe the solar system of gravitational fields based on the planet orbits，by calculating the precise gravitational value (the differences caused by theN-body gravity) of triangular Lagrangian pointsL4andL5using perturbation theory.Through the qualitative and quantitative analysis on the perturbation law of Lagrangian points，the conclusion about their sources，periodicity and so on could provide a reference for related research.

Lagrangian points；N-body problem；numerical study

2016-04-21

刘媛琪(1995—)，女，山东泰安人，大学本科生，主持国家级大学生创新创业训练项目，研究方向为以拉格朗日点相关问题为主的天体力学。

刘媛琪，周珊羽，巩子嘉.N体问题下日地三角拉格朗日点的数值研究[J].导航定位学报，2016，4(4)：5-11.(LIU Yuanqi，ZHOU Shanyu，GONG Zijia.Numerical study on Sun-Earth Lagrangian points ofN-body problem[J].Journal of Navigation and Positioning，2016，4(4)：5-11.)

10.16547/j.cnki.10-1096.20160402.

P128.1

A

2095-4999(2016)04-0005-07