物质粒子代数目NG的起源

许 陶，罗 睿

浙江大学物理学系，浙江杭州 310027



【物理与应用物理 / Physics and Applied Physics】

物质粒子代数目NG的起源

许 陶，罗 睿

浙江大学物理学系，浙江杭州 310027

在基本粒子物理的标准模型中，代数目的起源一直是悬而未决的问题．概述标准模型中3代费米子的确定以及代的物理背景，并讨论了利用规范反常消除条件在超对称大统一框架下探究代数目的可能性．超对称模型中的代数目依赖于大统一框架中的群结构．

物理学；代数目;规范反常消除;标准模型；超对称；大统一理论

1 代的发现和确定

20世纪50年代通过对弱相互作用的深入研究发现，下夸克的弱衰变强度和电子以及缪子的弱衰变强度差不多，但奇异夸克的弱衰变强度仅为预期的约1/4．为解释这一现象，1963年Cabibbo[1]提出弱相互作用的强度应该是普适的，但下夸克和奇异夸克之间若存在混合，就可以解释奇异夸克的弱衰变问题．换句话说，参与弱相互作用的是强相互作用下下夸克d和奇异夸克s本征态的混合态，即

d′=dcos θc+ssin θc

(1)

其中，混合角θC被称为Cabibbo角，大小约为13°．此时，d′为弱相互作用下的本征态．

1973年Kobayashi等[3]为解释CP破坏提出了一个大胆的假设: 他们注意到1970年理论物理学家Glashow、Iliopoulos和Maiani为了解释实验上味道改变中性流(flavor-changing-neutral-current, FCNC)过程被显著压低的现象，提出可能存在第4种夸克即粲夸克，4种夸克可分成除了质量以外，量子数完全相同的两代(u, d)和(c, s)，这两代夸克之间如果存在混合，并由此出发可预言树图层次上FCNC过程不会发生，简称GIM机制[4]．在GIM机制的基础上，Kobayashi和Masukawa进一步提出，若还存在第3代夸克的话，描述这3代夸克混合的混合矩阵包含一个复相角，正好可以描述CP破坏现象．这一夸克混合矩阵通常被称为Cabibbo-Kobayashi-Maskawa(CKM)矩阵．标准模型中的夸克带电流部分的拉氏量可写为

(2)

其中，g为弱相互作用耦合常数；uiL=(uL, cL, tL)为左手上夸克；γμ为伽马矩阵；djL=(dL, sL, bL)为左手下夸克；W*μ为W波色子；VijCKM为CKM矩阵元，CKM矩阵为

其中，Vij矩阵元下标i和j分别为6种夸克u、d、c、s、t和b中的一种．

早在20世纪60年代就有学者发现自然界至少存在两代量子数完全相同的轻子结构，即电子和缪子以及其对应的中微子．1974年，丁肇中和Richter各自领导的实验组分别发现了由粲夸克构成的J/Ψ介子，从而证实了自然界也至少存在两代夸克的结构[5-6]．第3代费米子的实验突破首先来自带电轻子.1977年，Perl领导的实验组在实验室中产生了第3代带电轻子—— τ轻子，并探测到 τ轻子衰变的末态产物，同时很多迹象也显示 τ 轻子的衰变伴随着 τ中微子的产生[7]．这一工作证实了自然界至少存在3代轻子的结构．第3代轻子的发现让物理学家们对第3代夸克的存在满怀信心．1997年，Lederman领导的实验组发现了由底夸克即带负电荷的第3代夸克组成的 Y介子[8]．但之后的十多年里，实验物理学家们几经尝试也未能发现带正电荷的第3代夸克——顶夸克的存在．

经过近20年的不懈努力，1995年Tevatron在实验中发现了第6种夸克——顶夸克t，其质量约为173GeV，是目前已知最重的费米子，约为第2重的底夸克质量的30倍[9]．至此，实验上确立了自然界至少存在3代夸克和3代轻子的结构，而欧洲大型正负电子对撞机上对Z玻色子衰变宽度的测量以及宇宙学上的一些观测，都预示着参与弱相互作用的轻中微子只有3代，说明自然界中也许并不存在第4代的夸克和轻子．

2 标准模型及其扩展中的规范对称性

量子场论中，规范反常指树图具有的对称性在量子效应中被破缺．规范对称性没有规范反常的条件被应用于标准模型规范对称性的确定[10]．假设每一代标准模型的物质场 QiL、 uiR、 diR、 liL和eiR(物质场符号分别对应左手夸克二重态场、右手上夸克场、右手下夸克场、左手轻子二重态场和右手轻子场，i为对应的代)都在同样一种规范对称性下变换，即在规范对称性下的量子数与所处的代数无关．同时假设他们在U(1)规范对称性下所带的荷分别为q、 u、 d、 l和e，则在现有标准模型的规范对称性SU(3)C×SU(2)L结构下，U(1)规范对称性与强相互作用对称性SU(3)C，弱相互作用对称性SU(2)L，以及其自身所构成的规范反常消除条件分别为

(4)

其中，A[SU(3)C]2U(1)为与强相互作用的反常系数；A[SU(2)L]2U(1)为与弱相互作用的反常系数；A[U(1)]3为U(1)规范对称性自身的反常系数；ATrU(1)为与引力相互作用的反常系数．

由式(4)可确定除归一化因子外所有5个标准模型物质粒子的U(1)对称性量子数．同时汤川(Yukawa)耦合在U(1)对称性下不变，用H表示希格斯二重态，则满足对称不变的耦合形式表示为

(5)

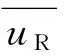
这进一步确定了希格斯粒子 H的在U(1)对称性变换下的荷．经此过程，该U(1)对称性被唯一确定了．所以标准模型的每代粒子，在假设没有其他规范对称性的情况下，即可唯一确定这一组U(1)超荷(hypercharge)．这是当代粒子物理标准模型规范对称性的重要基础．

然而，若引入代作为自由度，则会出现其他的无规范反常对称性．取无质量极限，物质场的拉格朗日量密度为

(6)

Qi→[UQ]ijQi

(7)

其中，[UQ]ij为幺正变换U的算符形式．

该对称性被破缺后遗留两个U(1)对称性以保证汤川耦合在变换下保持不变，即要求所有夸克和轻子分别有常数相因子变换，如Qi→eiαQi，ui→eiαui，di→eiαdi，li→eiβli，ei→eiβei．其中，α和β分别为常数相因子；U(1)B为重子数对称性；U(1)L为轻子数对称性．

表1为重子数与轻子数对称性的荷分配．

表1 重子数与轻子数对称性Table 1 Baryon number and Lepton number symmetry

根据表1中的U(1)荷可知，重子数和轻子数对称性都有非零的SU(2)L混合反常系数，即

(9)

这要求两个U(1)对称性只能作为整体对称性.与单独的对称性不同，不同代之间的轻子数差Li-Lj和重子数差Bi-Bj符合所有规范反常消除条件，则这类味对称性可成为理论中的规范对称性．

粒子物理的标准模型中，中微子是无质量的．但经过几十年关于中微子振荡效应实验的发展，已发现太阳中微子振荡、大气中微子振荡和反应堆中微子振荡等效应[11]，且有非常有力的证据说明中微子是有质量的．这也成为了超越标准模型物理的一个重要启示．在标准模型中要解释中微子质量，最简单的模型就是每一代引入1个右手中微子nj．

表2为重子数与轻子数之差所具有的对称性变换表．

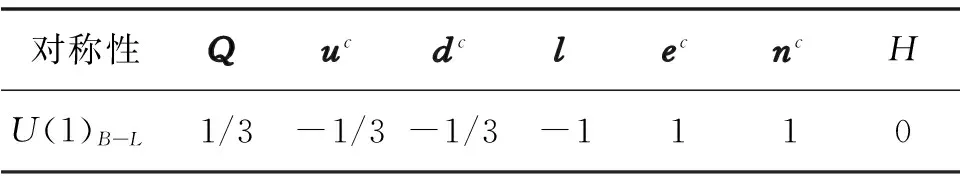
表2 B-L对称性Table2 Baryon number minus lepton number symmetry

通过表2中重新定义的U(1)B-L对称性，可发现所有的混合反常均被消除，即

(10)

其中，U(1)Y为标准模型中的超荷相互作用．

虽然右手中微子是标准模型规范对称性下的单态，但其带有的轻子数体现在U(1)B-L的规范反常消除中，即

(11)

则U(1)B-L规范反常完全消除，也可成为一个规范对称性.

右手中微子的引入，使另一个对称性SU(NG)也变成反常消除的规范对称性[12-13]．在此对称性下，NG代夸克轻子作为SU(NG)群下的一个NG重态进行变换．例如，设有3代物质粒子，则在SU(3)H下，3代左右手夸克分别构成3重态，即

(12)

类似于量子色动力学中QL和uR，dR构成左右对称的矢量规范理论．同理，右手中微子的引入使轻子部分也成为无规范反常的矢量规范理论，如式(13)．

(13)

在第一类翘翘板机制中需引入右手中微子的Majorana质量项[14]，其在破坏轻子数整体对称性的同时也破坏了U(1)B-L和SU(NG)规范对称性．其中，U(1)B-L被破坏成Z6子群．U(1)B-L的破缺，则依赖于右手中微子Majorana质量的结构．

3 规范R对称性与代数目NG

从规范反常消除条件可见，在标准模型中所有的规范反常系数均与代数目NG成正比，即使存在SU(NG)规范对称性也无法确定具体的代数目.

为了研究代数问题，可以在超对称理论模型中寻找启示.在最小超对称标准模型中，对应于标准模型SU(3)C×SU(2)L×U(1)Y规范对称性的规范场被提升为规范超场，而标准模型物质场在此模型中被提升为手征超场[15].超对称粒子的引入在规范反常消除中起到了重要作用.

(14)

在超对称势W中，规范对称性无法禁止若干破坏重子数B或轻子数L存在相互作用项[6]，即

(15)

其中，WΔL=1为包含轻子数破坏的势能项；WΔB=1为包含重子数破坏的势能项；i、 j和k为耦合系数带有的代指标；Li和Lj分别为第i和第j代轻子；λ、 λ′、 λ″和μ′分别为相互作用项耦合系数．

这些破坏重子数与轻子数的相互作用会导致实验中并未观测到的质子衰变过程，如p+→e+π0． 从其衰变宽度可明显看出，对重子数和轻子数改变耦合系数的依赖关系为

(16)

对这个问题一种解决方案是引入额外的对称性，禁止传递质子衰变等过程的相互作用.最简单的模型实现是R宇称[17]为

PR=(-1)3(B-L)+2s

(17)

其中，s为粒子自旋.

在此定义下，由于在超对称多重态中的分量场带有不同自旋，各分量场的R宇称彼此不同.所有标准模型粒子具有偶R宇称，即PR=-1，而超对称粒子具有奇R宇称，即PR=1.R宇称自然约束了超对称粒子需被成对产生，并在级连衰变的相互作用顶点中必须有偶数个超对称粒子出现，同时最轻超对称粒子成为了宇宙学暗物质的自然候选者.R宇称可以被认为是连续R对称性破缺至分立对称性ZNR后，在低能标留下的Z2R对称性.

Yanagida[18]指出，在包含ZNR及超对称粒子的特定模型中，新的规范反常消除条件能够确定代数目.但是，由于Z2R对称性在增加转动变换后可被重定义为一般Z2R分立对称性，R宇称并不是一个真正的R对称性[19].满足N阶离散ZNR群对称性阶数N≥3的分立对称性ZNR的是许多物理学家研究关注的重点．假设ZNR是物理学家规范R对称性的一个子群，并在SU(5)GUT大统一框架下进行讨论，每一代夸克和轻子超对称多重态分别对应用10和5*表示.根据对分立规范对称性的早期研究[20]，规范反常消除条件[18]为

(18)

其中，r10、 r5、 ru和rd分别为10和5*表示中的费米场及Hu和Hd的超荷.

因为在R对称性下不变的拉格朗日量应有的R荷为2，所以由汤川耦合给定的R荷条件为

(19)

联立方程组(18)和方程组(19)，可得到关于NG与ZNR分立对称性阶数N的约束方程

6-4NG=0(mod N)

(20)

由表3可读出不同粒子代数模型在规范反常消除条件下，能满足的分立R对称性阶数(NG>5的模型中存在朗道极点问题，限于篇幅不再赘述).

表3 SU(3)C和SU(2)L规范反常消除限制

Table 3 Constraints on SU(3)Cand SU(2)Lgauge anomaly cancellation

NG12345N1,21,21,2,3,61,2,5,101,2,7,14

该组分立对称性的阶数限制是在假设标准模型物质场的基础上确定的.若选取非平庸的物质场多重态个数，分立对称性的阶数可以被扩展[21].

值得注意的是，对应于SU(5)GUT大统一中质子衰变的5维算符10 10 10 5*所带的超荷为

3r10+r5=0(mod N)

(21)

当N≤3时，此算符在超对称势中被禁止．可见，分立R对称性有效解决了质子衰变危机.

代数的确定依赖于特定模型中的U(1)Y×ZNR规范反常消除条件[18].假设大统一群是一个半单群，且U(1)Y荷的归一化与标准模型相同，[U(1)Y]2×ZNR反常消除给出对代数的限制为

2×(-10NG+3)=0(mod N)

(22)

满足方程(22)的对称性阶数如表4．

表4 U(1)Y规范反常消除限制Table 4 Constraints on U(1)Y gauge anomaly cancellation

对比表3和表4发现，仅Z3R和Z6R同时满足规范反常消除条件与分立对称性要求.此时，3代条件被这一组超荷选取唯一确定．

值得注意的是，右手中微子nR的引入并不影响此U(1)Y对称性下的代数目确定过程.但是，右手中微子的Majorana质量及Dirac质量项对其荷r1进一步提出了要求,表示为

(23)

文献[9]指出，这种R对称性的荷选取并不满足特殊正交群SO(10)GUT大统一理论所要求的r1=r5=r10条件．对此，本研究拓展讨论SO(10)GUT大统一中的规范反常消除.一种直观理解SO(10)GUT群存在问题的方法是，联系第3节SO(5)GUT大统一的结果，并先假设r1=r5=r10为必要条件，则右手中微子质量及质子衰变禁止条件为

(24)

求解方程组(24)，可以发现在N=3、 4、 5约束条件下，唯一合理的一组解是r1=1，N=4.但显然可以由表3和表4比较得出，Z4R并不是一个能够满足规范反常消除的分立R对称性．这自然要求SO(10)GUT大统一框架下的规范反常消除问题需要被扩展.最新研究发现，在Z4R对称性的基础上，可以通过Green-Schwarz机制解决规范反常消除问题[22-24]．此机制利用引力反常系数AGravity，允许非零的规范反常出现，但同时需满足

(25)

其中，k1、 k2和k3分别为模型中的待定值．

Green-Schwarz机制解决了Z4R在大统一中的作用，且允许了更多ZNR对称性组合存在[25]．但是，根据本研究结果可知，此非零的规范反常系数并不用在代数目NG确定过程中起到作用．

结 语

阐述3代基本粒子在标准模型中的重要意义，每代粒子的规范反常贡献相消的重要理论基础，及中微子质量发现的重要启示，本研究围绕扩充费米场在规范反常消除中的作用进行论述．在最小超对称标准模型中，超对称粒子的规范反常贡献可在特定U(1)Y超荷选取下，确定NG=3． 对于超对称大统一框架中的规范反常系数处理，现阶段的理论模型仍未能将代数目及分立R对称性唯一确定．

/ References：

[1] Cabibbo N.Unitary symmetry and leptonic decays[J].Physical Review Letters, 1963,10(12): 531-533.

[3] Kobayashi M, Maskawa T.CP violation in the renormalizabletheory of weak interaction[J].Progress of Theoretical Physics, 1973, 49(2): 652-657.

[4] Glashow S L, Iliopoulos J, Maiani L.Weak interactions with lepton-hadron symmetry[J].Physical Review D: Covering Particles, Fields, Gravitation, and Cosmology, 1970,2(7): 1285-1292.

[5] Aubert J J, Becker U, Biggs P J, et al.Experimental observation of a heavy particle J[J].Physical Review Letters, 1974, 33(23):1404-1406.

[6] Augustin J E, Boyarski A, Breidenbach M, et al.Discovery of a narrow resonance in e+e-annihilation[J].Physical Review Letters, 1974, 33(23): 1406-1408.

[7] Goldhaber G, Pierre F, Abrams G S, et al.Observation in e+e-annihilation of a narrow state at 1865MeV/c2decaying to Kπ and Kπππ[J].Physical Review Letters, 1976,37(5):225-259.

[8] Herb S W, Hom D C, Lederman L M, et al.Observation of a dimuonresonance at 9.5GeV in 400-GeV proton-nucleus collisions[J].Physical Review Letters, 1977,39(5):252-255.

[10] Geng C Q, Marshak R E.Uniqueness of quark and lepton representations in the standard model from the anomalies viewpoint[J]．Physical Review D: Particles and Fields, 1989, 39(2): 693-696.

[11] Mohapatra R N, Antusch S, Babu K S, et al.Theory of neutrino: a white paper[J].Reports on Progress in Physics,2007, 70(11): 1757-1867.

[12] Yanagida T.Horizontal symmetry and masses of neutrinos[C]// Proceedings in Workshop on the Unified Theories and the Baryon Number in the Universe.Tsukuba, Japan:[s.n.], 1979, 7902131: 95-99.

[13] Yanagida T.Horizontal symmetry and masses of neutrinos[J].Progress of Theoretical Physics , 1980, 64:1103-1105.

[14] Mohapatra R N, Smirnov A Y.Neutrino mass and new physics[J].Annual Review of Nuclear and Particle Science,2006, 53(1): 44-82.

[15] Martin S P.A supersymmetry primer[EB/OL]．(1997-09-16).http://arxiv.org/abs/hep-ph/9709356.

[16] Nelson A E, Seiberg N.R symmetry breaking versus supersymmetry breaking[J].Nuclear Physics B, 1993, 416(1): 46-62.

[17] Weinberg S.The quantum theory of fields[M].影印版.3版.北京: 世界图书出版公司，2004: 183-184.Weinberg S.The quantum theory of fields[M].Facsimile reprint ed.3rd ed.Beijing: World Publishing Corporation,2004: 183-184.(in Chinese)

[18] Evans J L, Masahiro I, Kehayias J, et al.Nonanomalous discrete R symmetry decrees three generations[J].Physical Review Letters,2012, 109(18): 181801.

[19] Dine M, Kehayias J.Discrete R symmetries and low energy supersymmetry[J].Physical Review D: Particles and Fields,2010, 82(5): 055014.

[21] Harigaya K, Masahiro I, Schmitz K, et al.The peccei-quinn symmetry from a gauged discrete R symmetry[J].Physical Review D: Particles and Fields,2013, 88(7): 075022.

[22] Babu K S, Gogoladze I, Wang K.Natural R-parity, μ-term, and fermion mass hierarchy from discrete gauge symmetries[J].Nuclear Physics B,2003, 660(1/2): 322-342.

[23] Lee H M, Raby S, Ratz M, et al.Discrete R symmetries for the MSSM and its singlet extensions[J].Nuclear Physics B,2011, 850(1): 1-30.

[25] Paraskevas M, Tamvakis.Discrete R symmetries in the MSSM and its extensions[J].Physical Review D: Particles and Fields,2012, 86: 015009.

【中文责编：英 子；英文责编：木 南】

Investigation of the numberNGof matter particle generations

Xu Tao†and Luo Rui

Department of Physics, Zhejiang University, Hangzhou 310027, Zhejiang Province, P.R.China

In the standard model of particle physics, there are three generations of matter particles with identical quantum numbers but distinct masses.However,neither the answer to the question of whether there are only three generations of matter particles nor the origin of generation number is clear.We introduce the determination of three generations in the standard model and its physical background, and discuss the possibility of investigating the generation number in the supersymmetric grand unification framework.The generation number in the supersymmetric models depends on the grand unification group structure.

physics; generation number; gauge anomaly cancellation; standard model; supersymmetry; grand unification theory

O 412.3

10.3724/SP.J.1249.2016.06613

国家自然科学基金资助项目(11275168)

许 陶(1991—)，男，浙江大学博士研究生．研究方向：高能物理．E-mail: taoxu@zju.edu.cn

引 文：许 陶，罗 睿．物质粒子代数目NG的起源探讨[J].深圳大学学报理工版，2016，33(6)：613-619.