色噪声下的延时二阶预处理MUSIC算法

初 萍，张金凤

深圳大学信息工程学院，广东深圳 518060



【电子与信息科学 / Electronics and Information Science】

色噪声下的延时二阶预处理MUSIC算法

初 萍，张金凤

深圳大学信息工程学院，广东深圳 518060

为抑制色噪声对多信号分类(multiple signal classification, MUSIC)算法估计性能的影响，提出利用延时相关消除色噪声的二阶预处理方法．以L阶滑动平均(moving average, MA)模型为色噪声模型，利用大于L阶的延时相关函数为0的特点去除背景色噪声．为增加对多个入射信号成功分辨的概率，基于信号子空间估计稳健的特点，构造基于信号子空间加权的谱函数．提出的新算法无阵列孔径损失，不增加运算复杂度，因此，在色噪声背景下的实时波达方向(direction of arrival, DOA)估计中有较好应用价值．仿真实验表明，所提方法可有效抑制色噪声，在同样的估计条件下，该算法表现出较好的估计性能，且不增加计算量．

雷达工程；阵列信号处理；波达方向估计；色噪声；滑动平均模型；延时相关

波达方向(direction of arrival, DOA)估计是阵列信号处理领域重要的研究方向，在雷达、通信和声呐等领域均有广泛应用[1-3]．多信号分类(multiple signal classification, MUSIC)算法[4]是其中经典的子空间算法．它以高斯白噪声为背景噪声，利用噪声子空间与信号子空间的正交性实现对入射信号的波达方向估计，然而，现实测向系统中经常是色噪声环境，这就会严重影响MUSIC算法的估计性能，甚至导致算法失效[5-7]．因此，基于色噪声背景的波达方向估计也受到广泛的关注．

常用的解决色噪声问题的方法主要有：① 对噪声子空间分布进行估计，得到噪声子空间分布情况[8]，此类方法在很多情况下，存在噪声空间不能得到精确估计的问题，并且在实际测向系统中噪声子空间在不同时刻是不同的；② 利用预测和平移[9-10]等方法避开或消除色噪声的影响，此类方法经常会以阵列孔径的损失为代价；③ 利用高阶累积量[11]对色噪声的统计量为零的特点消除色噪声，高阶累积量方法可以避免上述两种方法的问题，但高阶累积量的复杂构造过程会大大增加计算的复杂度，降低系统的实时处理能力．

为此，本研究利用阵元间的延时相关函数去除色噪声对DOA估计的影响，同时得到了阵元数不变的新阵列对应的协方差矩阵，仿照MUSIC算法对新的协方差矩阵处理，并引入了信号子空间加权矩阵，增强了算法对入射信号的分辨能力．

1 信号模型

设空间有M个天线阵元组成的阵列，有P个不相关的窄带远场信号入射，信号与噪声相互独立，噪声为有色噪声，数据的快拍数为K，则阵列输出数据的矩阵用矢量形式可表示为

X=AS+N

(1)

其中，X为M×K维的阵列输出数据向量；A为M×P维的阵列流型；S为P×K维的入射信号向量；N为M×K维的色噪声向量．

由阵列输出数据的表达式，可得到阵列输出数据的协方差矩阵为

RX=E[XXH]=ARSAH+RN

(2)

其中，RS=E[SSH]为信号协方差矩阵，函数E[]为求期望操作；RN为噪声的协方差矩阵．

当阵列的输入噪声为高斯白噪声时，噪声协方差矩阵满足RN=σ2I的形式，σ2为噪声的功率，I为单位矩阵.对协方差矩阵 RX进行特征分解，得到由特征向量张成的信号子空间 US和噪声子空间 UN后，即可利用式(3)MUSIC算法的谱函数进行搜索得到信号的入射角度信息．

(3)

其中，a(θ)为阵列流型；θ为信号的入射角.

本研究讨论的阵列输入噪声为色噪声，与白噪声相比，色噪声不满足不同时刻不相关的特点，显然色噪声的协方差矩阵 RN已不满足对角阵且对角线元素相同的形式，如果仍简单地采用传统的MUSIC 算法对信号的入射角度进行估计，特征分解得到的信号子空间与噪声子空间不再满足正交关系，因而MUSIC算法的估计性能会严重下降甚至根本不能完成对入射信号的角度估计．

2 色噪声下的二阶预处理方法

因为在色噪声的情况下，MUSIC算法基本失效，因此研究采用基于滑动平均(moving average, MA)模型的色噪声预处理方法．

2.1 色噪声的延时预处理

在阵列信号处理的DOA估计方法研究过程中，色噪声的构造无统一格式，通常采用基于自回归 (auto regressive, AR)模型、MA模型及自回归滑动平均(auto regressive moving average, ARMA)模型等方法，本研究选取基于MA模型来构造色噪声，具体定义如下：

假设入射信号与阵列输出数据中的色噪声不相关，不同阵元间的色噪声亦不相关，则基于L阶的MA模型的第m个阵元上色噪声的表达式[12]为

nm(n)=a0w(n)+a1w(n-1)+…+

aLw(n-L)

(4)

由此可得nm(n)的相关函数表达式为

(5)

由式(5)可知，当基于MA模型色噪声相关函数的延时l大于色噪声的阶数L时，色噪声的延时相关函数值为0，即可以利用大于色噪声阶数的延时相关函数来消除阵列接收数据的色噪声．

然而，阵列的输出数据中色噪声并不是独立于入射信号而存在的，所以需要结合本小节的结论研究在阵列接收数据中去除色噪声的方法．

2.2 阵列接收数据的延时相关函数

本研究以M元均匀线阵为例，研究阵列接收数据的延时相关函数，阵元间距为d，第1个阵元是参考点，位于原点，设空间有P个入射信号，入射信号间不相关，则阵列的导向矢量可表示为

a(θi)=[1, exp(-j2πdsin θi/λ), …,

exp(-j2π(M-1)dsin θi/λ)]T

(6)

其中，θi为第i(i=1,2, …, P)个信号的入射角度，λ为入射信号的波长．于是，阵列流型可以表示为

A=[a(θ1)，a(θ2)，…，a(θP)]

(7)

结合阵列输出数据的矩阵表达如式(1)，可得到第m个阵元的接收数据表达式为

xm(n)=AmS(n)+nm(n)

(8)

结合式(6)和式(7)，可得矩阵 Am(m=1,2, …, M)的表达式为

Am=[am(θ1), am(θ2), …, am(θP)]=

[exp(-j2πdsin θi/λ), …,

exp(-j2π(M-1)sin θi/λ)]T

(9)

且有

A=[AT1，AT2，…，ATM]

(10)

假设nm(t)是基于L阶的MA模型的色噪声，阵元间噪声不相关，可得到第m(m=1,2, …, M)个阵元的接收数据与第1个阵元之间的延时相关函数为

(11)

根据前述色噪声延时相关函数的结论可知，若取延时l满足l >L，则可得式(11)中的rm1(l)=0，于是有

Rxmx1(l)=AmRS(l)

(12)

在l >L的条件下把每个阵元与第1个阵元的延时相关函数写成矩阵形式为

RXx1(l)=[A1T, A2T, …, AMT]RS(l)=

ARS(l)

(13)

参考上述推导，同样取l >L推导第m个阵元与第k个阵元间的延时相关函数为

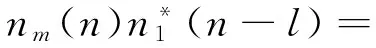
Amdiag(A*k)RS(l)

(14)

于是，阵列每个阵元的接收数据与第k个阵元间的延时相关函数写成矩阵形式为

RXxk(l)=Adiag(A*k)RS(l)

(15)

2.3 阵列接收数据的重新构造

结合式(1)与式(15)可知，当延时l >L时，阵列的接收数据与第k个阵元间的延时相关函数可以看作阵列流型为 Adiag(A*k)，入射信号为 RS(l)的一个新阵列的输出．于是可得阵列与第k个阵元的延时相关函数的导向矢量为

ak=Adiag(A*k)θi=

{exp[-j2π(1-k)sin θi/λ]

exp[-j2π(2-k)sin θi/λ] …

exp[-j2π(M-k)dsin θi/λ]}T

(16)

即新阵列的阵列流型为Adiag(A*k)，而导向矢量为其中的一列，角度是未知的θi． 同理，可得阵列与第M-k+1个阵元的延时相关函数的导向矢量为

aM-k+1=Adiag(A*M-k+1)θi=

[exp(j2π(M-k)sin θi/λ) …

exp(j2π(2-k)sin θi/λ)

exp(j2π(1-k)dsin θi/λ)]T

(17)

由式(16)和式(17)可知，阵列与第k个阵元和与其第M-k+1个阵元的延时相关函数的导向矢量满足

Adiag(A*k)θi=flipup[Adiag(A*M-k+1)θi]*

(18)

其中，flipup表示矩阵上下倒序翻转．

于是，若用倒序的阵列接收数据与第M-k+1个阵元求取延时相关函数，则有

RX′xM-k+1(l)=flipup[Adiag(A*M-k+1)]RS(l)=

[Adiag(A*k)]*RS(l)

(19)

其中，X′表示阵列接收数据按阵元位置的反序．

于是可构造新的阵列协方差矩阵为

Rk(l)=RXxk(l)RHXxk(l)+R*X′xM-k+1(l)[R*X′xM-k+1(l)]H=

Adiag(A*k)RS(l)RHS(l)[Adiag(A*k)]H+Adiag(A*k)R*S(l)RTS(l)[Adiag(A*k)]H=

Adiag(A*k)[RS(l)RHS(l)+R*S(l)RTS(l)][Adiag(A*k)]H=

Adiag(A*k)RSS(l)[Adiag(A*k)]H

(20)

其中，RSS(l)=RS(l)RHS(l)+R*S(l)RTS(l)=2Re[RS(l)RHS(l)]．

由式(20)可得到新的协方差矩阵．对式(20)进行特征分解，仿照式(3)，即可通过谱峰搜索得到信号的入射角度．由式(20)的构造又可知，有M个阵元的阵列，并可得到k组结果.其中，当M为偶数时，k=1,2, …, M/2；当M为奇数时，k=1,2, …, (M+1)/2． 将k组的搜索结果求取统计平均可以提高搜索精度．

3 色噪声下二阶延时预处理的谱函数

由式(20)可知，通过阵列数据与某个阵列的延时相关函数可得到新的协方差矩阵，仿照MUSIC算法的处理过程可搜索得到信号入射角度信息，因此对基于延时相关函数的MUSIC算法谱函数进一步分析以得到对入射信号更好的分辨能力．

3.1 基于延时二阶预处理的谱函数

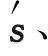
(21)

3.2 信号子空间加权的谱函数

由式(21)可见，特征分解得到的信号子空间及特征值等结果并未在谱函数中有充分应用，而且信号子空间处理具有稳健性高的特点，文献[13]也证实了信号子空间的加权可以提高MUSIC算法谱函数的分辨能力，并给出了加权矩阵的选取方法．本研究仿照子空间加权的方法将式(21)谱函数改写为

(22)

(23)

于是，在阵元间延时相关阶数大于色噪声阶数L的情况下，通过对接收数据的二阶预处理及新的协方差矩阵的构造，可得到去除色噪声的延时二阶预处理MUSIC方法(CLR2nd-MUSIC算法)．

4 仿真实验

通过仿真验证本研究提出的CLR2nd-MUSIC算法，并通过与MUSIC算法及累积量方法对比，以期说明所提方法的估计性能．实验过程中采用的阵列是间距为半波长的3阵元均匀线阵，入射信号数为2，噪声采用阶数为10的MA模型的色噪声．

4.1 算法的分辨力仿真实验

实验1对3种方法的谱函数图进行比较．信号入射角度分别设为1.5°和-1.5°，实验中信噪比设置为20dB，快拍数为500，1次实验的谱函数图如图1．其中，纵坐标P表示3种算法以dB为单位的谱值．

图1 三种方法的谱函数图Fig.1 Spectrum functions of three methods

由图1同条件下3种不同算法的谱函数图可见，在色噪声条件下，MUSIC算法仅1个谱峰，不能分辨出入射信号，而累积量方法及本研究提出的CLR2nd-MUSIC算法则可清晰分辨出两个信号，且CLR2nd-MUSIC算法的谱峰与峰谷位置对比明显．

实验2信噪比、快拍数对分辨能力的影响．当信号入射角度为1.5°和-1.5°，快拍数为500时，不同信噪比情况的分辨成功概率如图2．当信噪比为15dB时，不同快拍数情况下的分辨成功概率如图3．

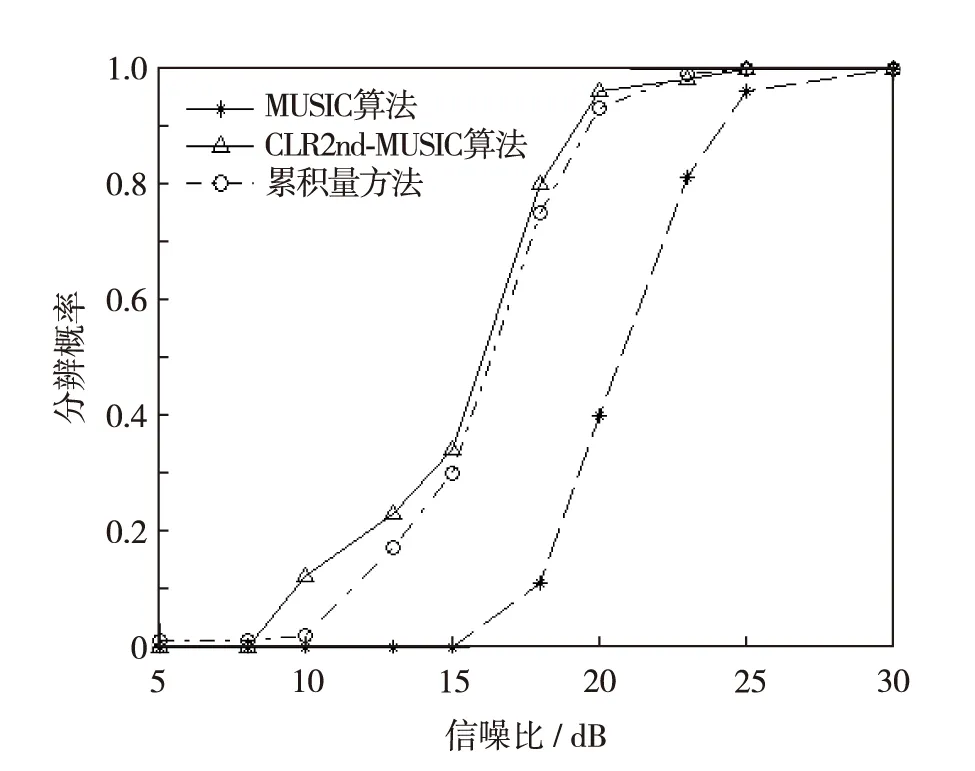
图2 不同信噪比条件下的分辨概率Fig.2 Resolution probability with different SNR

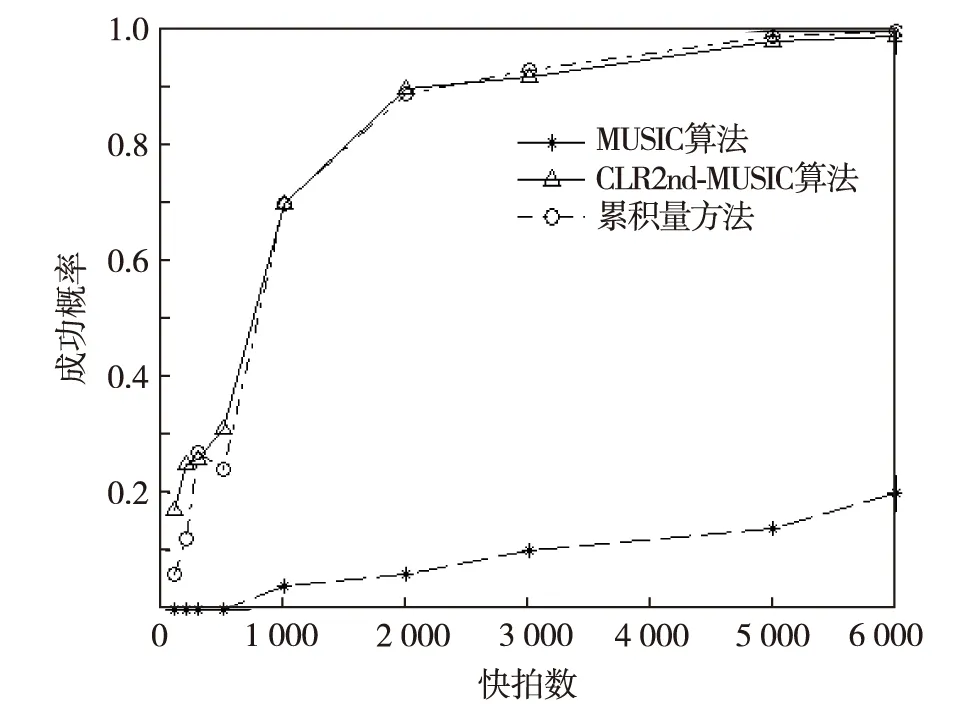
图3 不同快拍数条件下的分辨概率Fig.3 Resolution probability with different number of snaps

由图2和图3的仿真结果可见，在信噪比较低的情况下，MUSIC算法对入射信号的分辨概率很低，CLR2nd-MUSIC算法和累积量方法分辨概率均随信噪比与快拍数的增加而增加，体现出较好的分辨性能．累积量方法以色噪声的高阶累积量为0的原理来抑制色噪声，CLR2nd-MUSIC算法则以高于色噪声阶数的延时相关函数为0的原理来抑制色噪声，两者本质上都是通过抑制色噪声来提高分辨概率，所以分辨能力相近，仿真结果也表明两者的分辨概率相近．

实验3不同信号入射间隔对成功概率的影响．两个入射信号对称分布在视轴两侧，快拍数设置为500，信噪比为15dB，仿真结果见图4．

图4 不同角度间隔的分辨概率Fig.4 Resolution probability with different angle interval

由图4可见，MUSIC算法不能对信号间距小于5°的两个信号进行分辨，而CLR2nd-MUSIC算法和累积量方法在角度间隔大于3°的情况下已经表现出较好的估计性能．

综合实验1到实验3的仿真结果，显然在色噪声背景下，MUSIC算法难以实现对入射信号的分辨，而累积量方法及CLR2nd-MUSIC算法均能在没有孔径损失、不预先估计噪声空间的情况下，实现对入射信号的分辨且估计性能相近．

4.2 算法的运算量仿真实验

由算法的分辨力仿真结论可以看出，累积量方法及CLR2nd-MUSIC算法对色噪声均能体现出较好的抑制作用．为此，对算法的运算量复杂度进行分析，并通过仿真实验进行验证．

对实验中3种算法的运算复杂度进行协方差的计算、特征值分解及谱峰搜索3个主要步骤分析，见表1．

表1 三种算法的运算复杂度1)Table 1 Computational complexity of three methods

由表1可见，与MUSIC算法相比，CLR2nd-MUSIC算法仅在构造协方差矩阵时有复数乘加运算次数的增加，其余步骤均无计算量的增加，而累积量算法在角度估计的各个步骤中均增加了大量的运算复杂度．

实验4运算时间的比较．在计算机相同的运行条件下，对3种方法估计2个入射信号所消耗的时间进行统计，结果如表2．

表2 相同运行条件下3种方法的计算时间

Table2 Computing times for three methods under same operation condition

s

由表2可见，在相同的计算机运行条件下，CLR2nd-MUSIC算法的计算时间比MUSIC算法仅有少量的增加，即新方法在特征分解前需要通过二阶的延时预处理构造新的协方差矩阵，仅增加少量的计算量，而累积量方法计算量明显多于另外两种方法，这与表1中算法运算复杂度的分析一致．由实验1到实验3的结论可明显看到，与MUSIC算法相比，累积量方法及CLR2nd-MUSIC算法均可有效抑制色噪声，但从综合运算复杂度方面考虑，后者估计性能更优．

结 语

在色噪声背景下，MUSIC算法的估计性能严重下降，本研究对基于MA模型的色噪声背景下的角度估计方法进行了研究，通过构造大于L阶的延时相关函数得到新的协方差矩阵，对该协方差矩阵进行处理，得到CLR2nd-MUSIC算法的谱函数．仿真实验证明本研究所提出的方法有效，且其估计性能比累积量方法的估计性能更优越．

/ References：

[1] Gong J, Lou S, Guo Y.ESPRIT-like algorithm for computational-efficient angle estimation in bistatic multiple-input multiple-output radar[J]．Journal of Applied Remote Sensing,2016, 10(2)： 025003.

[2] Werner J, Wang Jun, Hakkarainen A, et al．Performance and cramer-rao bounds for DoA/RSS estimation and transmitter localization using sectorized antennas[J]．IEEE Transactions on Vehicular Technology，2016，65(5): 1-1.

[3] Saucan A A, Chonavel T, Sintes C, et al.CPHD-DOA tracking of multiple extended sonar targets in impulsive environments[J].IEEE Transactions on Signal Processing,2016, 64(5): 1147-1160.

[4] Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation, 1986, 34(3):276-280.

[5] 洪 升，万显荣，柯亨玉．空间色噪声背景下双基地多输入多输出雷达低仰角估计方法[J]．电子与信息学报，2015，37(1)：15-21． Hong Sheng, Wan Xianrong, Ke Hengyu.Low-elevation estimation for bistatic MIMO radar in spatially colored boise[J].Journal of Electronics and Information Technology ,2015, 37(1): 15-21.(in Chinese)

[6] Hassen S B, Bellili F, Samet A, et al.DOA estimation of temporally and spatially correlated narrowband noncircular sources in spatially correlated white noise[J].IEEE Transactions on Signal Processing,2011, 59(9): 4108-4121.

[7] 赵春晖，马 爽，成宝芝.基于特征值矩阵的循环平稳检测算法[J].深圳大学学报理工版，2012，29(2)：107-112.Zhao Chunhui, Ma Shuang, Cheng Baozhi.Cyclostationary spectrum sensing algorithm based on eigenvalues matrix[J].Journal of Shenzhen University Science and Engineering,2012,29(2): 107-112.(in Chinese)

[8] 司伟建，林晴晴．一种稳健的非圆信号波达方向估计算法[J]．系统工程与电子技术，2013，35(3): 469-473.Si Weijian, Lin Qingqing.Robust direction finding algorithm for non-circular signals[J].System Engineering and Electronics,2013, 35(3): 469-473.(in Chinese)

[9] 刘晓莉，廖桂生．基于MUSIC和ESPRIT的双基地MIMO雷达角度估计算法[J]．电子与信息学报，2010，32(9):2179-2183． Liu Xiaoli, Liao Guisheng.Combined MUSIC with ESPRIT algorithm for angle estimation in bistatic MIMO radar system[J].Journal of Electronics and Information Technology,2010，32(9):2179-2183.(in Chinese)

[10] 贺成龙，秦 洪，于永生．一种空中目标航迹的自适应跟踪算法[J]．深圳大学学报理工版，2014，31(4):361-366． He Chenglong, Qin Hong, Yu Yongshen.An adaptive tracking algorithm for aerial target [J].Journal of Shenzhen University Science and Engineering,2014, 31(4): 361-366．(in Chinese)

[11] 陈 华，王安国，姬雨初，等．一种改进的四阶累积量测向算法[J]．西安交通大学学报，2012，46(12)：36-41． Chen Hua, Wang Anguo, Ji Yuchu, et al.Improved cumulant direction finding algorithm with foruth order[J].Journal of Xi’an Jiao Tong University,2012, 46(12): 36-41.(in Chinese)

[12] 张 奕，殷福亮．混响和有色噪声环境下的顽健时延估计方法[J]．通信学报，2008，29(5)：6-12． Zhang Yi, Yin Fuliang.Robust time-delay estimation in highly adverse acoustic environments[J].Journal of Communications,2008,29(5): 6-12.(in Chinese)

[13] Viberg M，Ottersten B, Kailath T.Detection and estimation in sensor arrays using weighted subspace fitting[J].IEEE Transactions on Signal Processing, 1991, 39(11):2436-2449.

[14] 丁 齐，魏 平，肖先赐．基于四阶累积量的DOA估计方法及其分析[J]．电子学报，1999，27(3)：25-28． Ding Qi, Wei Ping, Xiao Xianci.Estimation and analysis of DOA based on fourth-order cumulant[J].ACTA Electronica Sinica, 1999,27(3):25-28.(in Chinese)

【中文责编：英 子；英文责编：子 兰】

Delay second order preprocessing MUSIC algorithm in presence of colored noise

Chu Ping†and Zhang Jinfeng

College of Information Engineering, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China

In order to avoid the effect of colored noise in multiple signal classification (MUSIC) algorithm, we propose a second order preprocessing method with delay correlation function.We eliminate colored noise by choosing a moving average (MA) model with L orders and constructing a delay correlated function that equals zero when its order is more than L.We construct a new weighted spectrum function based on the robust estimation performance of signal subspace in order to improve the resolving probability.The proposed algorithm improves estimation performance without loss of array aperture and complex computation.Hence, it has better application value in real direction of arrival (DOA) estimation with colored noise.Simulation results show that the proposed algorithm can eliminate colored noise effectively, and it has a better estimation performance without additional computation under the same estimation conditions.

radar engineering; array signal processing; direction of arrival estimation; color noise; moving average model; delay correlation

TN 953

10.3724/SP.J.1249.2016.06571

国家自然科学基金资助项目(61501301)；广东省科技计划资助项目(2013B021500017)

初 萍(1983—)，女，深圳大学讲师、博士．研究方向：雷达阵列信号处理．E-mail：chuping@szu.edu.cn

引 文：初 萍，张金凤．色噪声下的延时二阶预处理MUSIC算法[J].深圳大学学报理工版，2016，33(6)：571-577.