数学建模及仿真在高等数学教学中的应用研究

王 晶

(蚌埠学院 数学与物理系，安徽 蚌埠 233030)

数学建模及仿真在高等数学教学中的应用研究

王 晶

(蚌埠学院 数学与物理系，安徽 蚌埠 233030)

讨论了在高等数学教学中融入建模思想和仿真方法的必要性，通过案例分析阐述了如何在教学过程中融入建模思想和仿真方法。进而提出了几点注意事项，以便更好地培养学生的建模思维和应用能力。

高等数学；数学建模；数值仿真；教学研究；建模案例

数学知识解决实际问题，是一个建立数学模型，求解模型，分析和验证结论的过程。所以，在高等数学的教学过程中，教师不仅要讲授基本的数学概念和计算方法，还要把数学建模思想及数值仿真方法贯穿其中。通过数学建模使学生认识到，数学能够解决社会生活中的实际问题。通过数值仿真能够使学生更加直观的观察参数的变化对问题解的影响。教学中，教师可以利用建模案例加深学生对概念的理解和方法的掌握，提升他们对高等数学应用价值的认识，提高他们的学习兴趣，培养他们的创新思维和应用能力[1]。

1 教学中融入建模思想及仿真方法的必要性

传统的高等数学教学以教师为主，采取灌输式的教学方法，教师侧重对教材中例题和习题的讲解，通过题海战术培养学生做题的能力和水平。但往往忽视数学知识在解决实际问题中的作用，给学生一种数学知识只能用来做题的错觉，毫无学习动力。所以，教学过程显得枯燥乏味，死板单一，教学效果较差。为了激发学生的学习积极性和主动性，应该转变教学观念，以问题为导向，让学生在对问题的解决中加深对知识的理解，增强他们的应用能力[2]。

目前的数学教学，不但要让学生掌握扎实的基础知识和严谨的数学逻辑思维，而且更要注重培养学生分析问题、解决实际问题的应用能力，学以致用。因此，教学过程中，让学生利用数学建模思想及仿真方法对实际问题进行综合分析、抽象、归纳、推理和计算，构建最优的数学模型并求解。若模型无解析解，则可采用Matlab软件求数值解[3]。由此可见，数学建模是利用数学知识解决实际问题的一个有效途径，数值仿真则是展现模型解的一个具体化、形象化的有效工具。它们都是培养学生应用能力和创新能力的正确措施。

2 如何在教学中融入建模思想及仿真方法

在高等数学教学中，教师往往轻视建模思想的融入和仿真方法的使用，只注重基础理论的传授和解题技巧及方法的训练。这样的教学模式导致理论与实践脱节，使学生错误的认为一支笔和一张纸就是高等数学，学习的目标就是做题。对于为什么要学习高等数学？学这门课有何作用？怎样才能学好这门课？等等。对这些问题，学生没有清醒的认识，始终处于迷茫之中。针对学生眼中“无用武之地”的高等数学，教师在日常的教学活动中必须把实用性潜移默化地传授给学生，让学生明确学习的目标。因此，教师必须把建模思想及仿真方法融入教学中，以解决实际问题促进知识的传授和能力的培养。同时，更要让学生明白高等数学也可以借助信息技术展现更加直观的数值结果，而不仅仅是笔与纸的简单交互。

根据自身高等数学教学经验，结合社会生活中的实际问题，给出两个具体建模案例来说明建模思想及仿真方法在教学过程中的应用。

案例1：金融系统的微分方程模型。

提出问题：现实金融系统中，利率、投资需求和价格指数之间存在一种相互制约、相互影响的关系。并且以上三者还受到储蓄量和单位投资成本等因素的制约。考虑它们之间量化关系的基础上，在给定变量值的前提下，观察该金融系统在运行过程中的稳定性问题，以及参数的变化是否会引起系统的动荡？

针对这个实际问题，首先引导学生进行思考，使学生意识到一般的数值运算很难解决此类问题。其次，再构建模型，并利用数值仿真的方法才能较完美的解决此问题。

建立模型：设利率为x，投资需求为y，价格指数为z，储蓄量为a，单位投资成本为b，商品需求弹性为c(a,b,c均为正常数)。则建立的微分方程模型如下[4]：

(1)

高等数学中所讲授的微分方程组的求解方法，一般针对特定的几种类型，而现实中的微分方程模型往往比较复杂，不一定符合某一种特定的类型。所以，教材中的求解方法远远不能满足实际需求，在微分方程组无解析解时，可以利用Matlab软件求得数值解，并借助图形展示求解结果。

下面，对模型(1)利用Matlab软件进行求解和仿真[5]。变量取值为：a=0.9，b=0.2，c=0.5；初值分别为x(0)=0.5，y(0)=0.2，z(0)=0.6。仿真结果如图1-图3所示。

通过图1和图2可以让学生很直观的得知，利率x，投资需求y和价格指数z，在系统运行过程中一直处于周期波动状态，即呈现周期解。通过图3可以使学生更形象地观察到，随着储蓄量a和单位投资成本b的增加，利率x上下波动较大，动荡明显。

图1 利率x，投资需求y和价格指数z的时间序列图

通过案例1的讲解，可以使学生对建模和仿真有一个直观的认识和深刻的体会，能够大大激发学生对数学知识的好奇心和求知欲，增强对高等数学实用性的理解。

案例2：渔业生物经济模型。

提出问题：渔业市场中，渔业资源的总量、工人的捕捞努力量和鱼价之间存在着密切的关系。当鱼价较高时，为了追求利润，捕捞量增加必然导致鱼资源量减少；而当鱼价较低时，无利可图，捕捞量减少将导致鱼资源量增加。这是一个复杂的博弈过程，随着博弈的进行，二者将最终趋于稳定，达到彼此都可以接受的平衡状态。考虑渔业资源的总量、工人的捕捞努力量之间的关系，在给定变量值的基础上，量化鱼价对渔业资源量和捕捞努力量的影响。

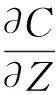
(2)

为了说明鱼价p对渔业资源量S和捕捞努力量Z的影响，借助Matlab软件进行数值仿真。

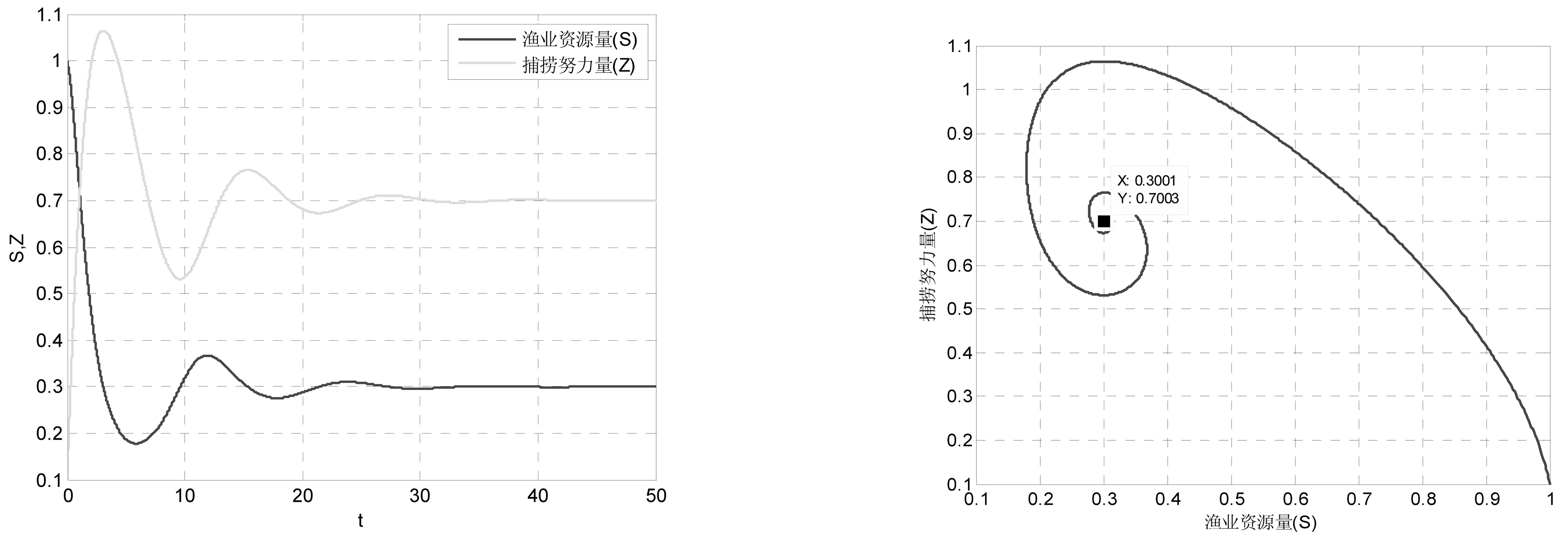
图4 p=1时渔业资源量S和捕捞努力量Z的时间序列 图5 p=1时渔业资源量S和捕捞努力量Z的吸引子

学生从图4可以形象的看出，随着时间的延长，渔业资源量S和捕捞努力量Z由不稳定的波动状态都逐渐趋于稳定状态，最后分别稳定在约0.3和约0.7。图5则更明确的说明二者经过长期博弈后，最终稳定在了S=0.3001,Z=0.7003。

(2)设p=0.5，其他变量值不变。则数值仿真如图6和图7所示。

图6 p=0.5时渔业资源量S和捕捞努力量Z的时间序列 图7p=0.5时渔业资源量S和捕捞努力量Z的吸引子

学生通过图6很容易看出，随着时间的增加，渔业资源量S和捕捞努力量Z也都由不稳定的波动状态逐渐趋于稳定状态，最后分别稳定在约0.6和约0.4。与图4相比可以看出，在鱼价较高时(p=1)，刚开始捕捞努力量增加明显，导致渔业资源量加速减少；在鱼价较低时(p=0.5)，则恰恰相反。图7则更准确的说明二者经过博弈，最终稳定在了S=0.5996,Z=0.4003，此时整个系统是平衡的，渔业生态是良好的。

学生从图8则可以看出，随着鱼价p的增加，捕捞努力量Z逐渐增大，而渔业资源量S则逐渐减少，这符合基本的生活常识。图形显示，可以让学生更直观、更具体的感受到结论的真实性。

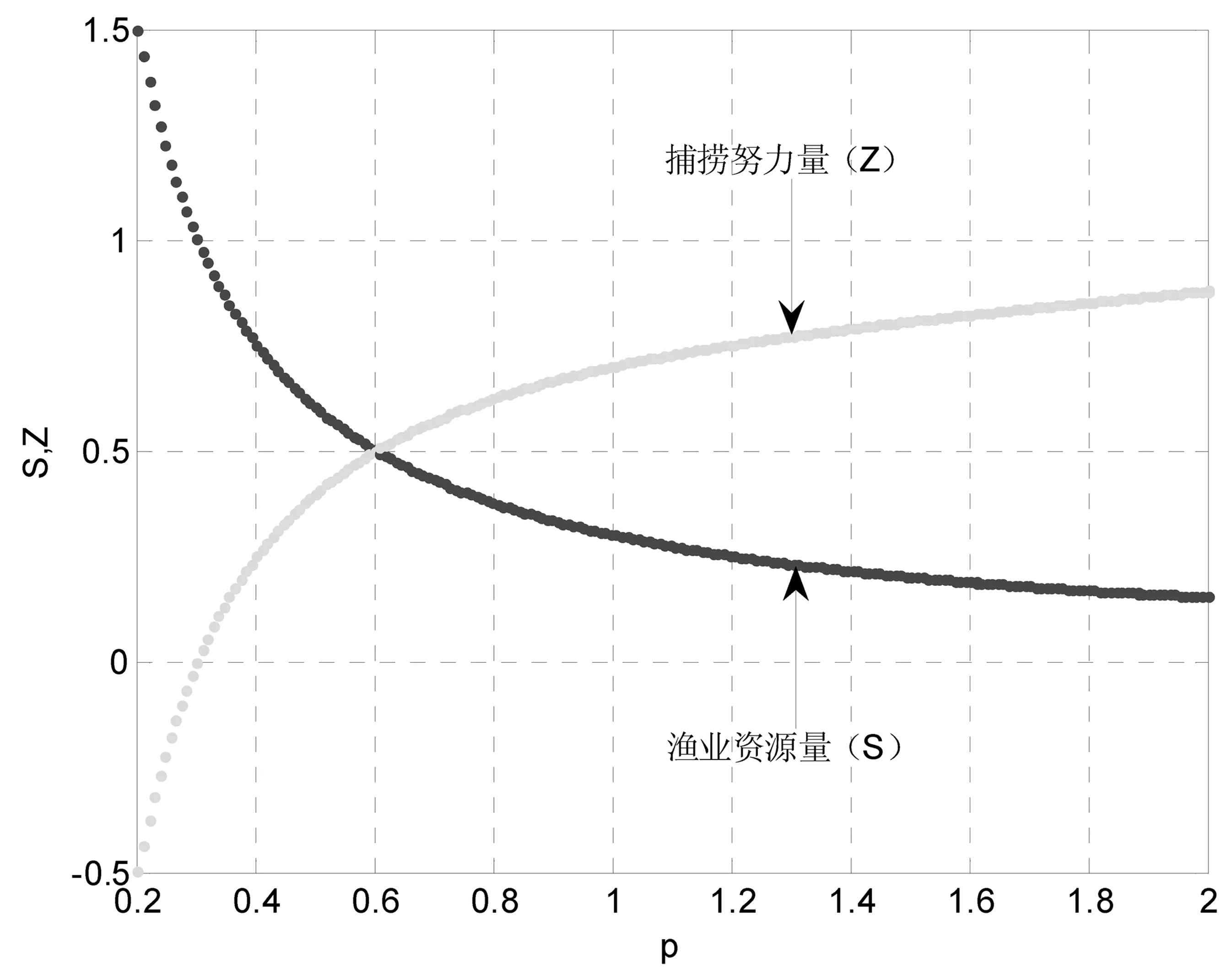
图8 鱼价p对渔业资源量S和捕捞努力量Z的影响

通过以上两个建模案例的讲解，不但让学生体会到了建模的思想和数值仿真的方法，而且在解决实际问题的过程中，加深了学生对微分方程的理解和应用，明确了高等数学是实用性很强的课程，增强了他们学习信心。

3 在教学过程中融入建模思想和仿真方法应注意的问题

在教学过程中，适当引入建模案例可以使学生感受到数学在解决实际问题中的巨大作用，有效提高学生的学习兴趣和学习动力。同时，还可以培养学生的数学思维、分析问题与解决问题的能力[7]。

(1)授课过程中，教师在讲解基础知识的基础上，再适当引入生活中的建模案例比较恰当。在讲解案例时，最初不要过于重视细节，让学生从整体上体会建模的过程和数值仿真的效果。这可以有效地向学生传输建模的思想和数值仿真的方法，让学生感受数学的魅力。

(2)讲解案例要有明确的目的性和针对性。应选取高等数学中典型的教学内容，有针对性的选择或设计案例，通过案例的讲解使学生加深对专业知识的理解，引导学生利用所学知识去解决实际问题。

(3)处理好授课内容与数学建模之间的关系。建模思想的融入和数值方法的使用，是建立在学生掌握扎实基础知识之上的，因此，教师应该在教授基础知识和基本技能的前提下，借助建模案例加深学生对基础知识实用性的理解。切记在教学过程中，把建模思想和仿真方法作为重点内容来讲，而无视正常的教学内容。

4 结束语

本文通过案例讨论了在教学过程中融入数学建模思想和仿真方法的必要性和可操作性，优化了教学方法和手段。教学实践证明，这种转变不但可以培养学生的数学思维，而且能够提高学生解决实际问题的能力，增强学生学习高等数学的积极性和主动性，取得了良好的教学效果。

[1] 孙露．高等数学思维型课堂教学模式的建构与实践[J]．内蒙古师范大学学报(教育科学版)，2015，28(12)：138-141．

[2] 官春梅．渗透数学建模思想于高等数学课程教学中的探究[J]．喀什师范学院学报，2015，36(6)：67-69．

[3] 吕颖，蒋观敏．数学建模课程的教学改革探讨[J]．西南师范大学学报(自然科学版)，2015，40(12)：173-175．

[4] 宋银芳．一类混沌金融系统的反馈控制[J]．重庆邮电学院学报(自然科学版)，2006，18(12)：796-799．

[5] 孔祥强．基于Matlab软件的高等数学教学可视化研究[J]．长春大学学报，2015，25 (10)：51-54．

[6] 刘召芳，常宗瑜．简单渔业生物经济动力学模型的稳定性分析[J]．渔业经济研究，2006(3)：2-5．

[7] 闵兰，陈晓敏．高等数学教学改革的几点思考[J]．西南师范大学学报(自然科学版)，2012，37(2)：139-141．

[责任编辑：崔海瑛]

王晶(1981-)，女，湖北广水人，讲师，从事微分方程及高等数学教学方面研究。

安徽省省级教学研究项目(2015jyxm386)

G642.0

A

2095-0063(2016)06-0138-04

2016-05-22

DOI 10.13356/j.cnki.jdnu.2095-0063.2016.06.030