单相LCL并网逆变器新型电流控制策略研究
杨旭红,王创典,何超杰,李浩然,王毅舟
(上海电力学院自动化学院,上海 200090)
单相LCL并网逆变器新型电流控制策略研究
杨旭红,王创典,何超杰,李浩然,王毅舟
(上海电力学院自动化学院,上海 200090)
LCL型并网逆变器是一个3阶多变量系统,并网电流单环控制难以满足系统的稳定性。为此提出了以电容电流为内环反馈,以并网电流为外环反馈的新型双环控制策略。内环采用比例调节增加系统阻尼以抑制高频谐振问题,外环采用模糊PR+重复控制在线调节系统干扰的影响,实现系统高电能质量并网。仿真和实验结果验证了该控制策略的可行性,并与PR+重复控制相比较,该控制策略具有良好的稳定性和鲁棒性。
滤波器;并网逆变器;重复控制;模糊比例谐振控制
逆变器是微电网并网的关键器件,并网逆变器的控制技术也逐渐成为微电网并网的重点。并网逆变器的控制根据控制对象可以大致分为3类:电流控制、电压控制、模拟同步电机控制,其中常见的是并网逆变器的电流控制。电流控制是指控制并网电流完成对电网电压同频同相的跟踪,同时满足系统输出的功率因数cosθ=1,并使并网电流的谐波畸变尽量小。因此对逆变器并网系统中的滤波器设计至关重要。与L型、LC型滤波器相比,LCL型滤波器具有体积小、成本小、损耗小的优点,且对高频谐波电流有较好的衰减作用,同时LCL型滤波器是三阶系统,阻尼较小,其引起的谐振问题成为目前研究的热点[1]。
逆变器电流控制策略常见的有PI控制、PR控制、重复控制、无差拍控制、滞环控制等[2]。针对LCL型逆变器系统的复杂性以及传统电流控制的局限性,文献[3]提出了一种重复+PI复合控制策略,PI环节在提高系统快速性的同时也存在相位误差。针对文献[3]中的问题,文献[4]采用了重复+PR复合控制策略,PR环节用以消除相位误差,但是PR控制器参数难以调整,无法自适应调节外界干扰对系统性能的影响。针对以上问题,本文提出一种新型的并网电流双环控制策略,以电容电流为内环反馈,采用比例调节增加系统阻尼以抑制高频谐振,以并网电流为外环反馈,采用模糊PR+重复控制在线调节系统干扰的影响,实现系统高电能质量并网。最后通过仿真验证了该控制策略的正确性。
1 单相LCL型逆变器数学模型
图1所示为LCL型滤波器的并网逆变器电路拓扑结构,其中微网新能源中的发电机用直流电源Udc替代,逆变器侧电感L1、电容C、主电网测电感L2构成LCL型滤波器,r1和r2为滤波电感的等效寄生电阻,Uo为逆变器输出端电压,Us为电网电压,igrid为并网电流,将网侧电压Us看作扰动变量,将并网电流igrid看作输出变量,逆变器输出电压Uo看作输入变量。
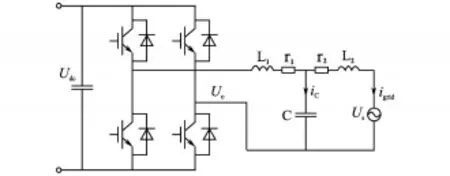
图1 单相LCL型并网逆变器拓扑结构Fig.1 Structure of single-phase LCL grid-connected inverter
由文献[5]可以得到并网电流igrid与逆变器输出电压Uo的函数表达式:
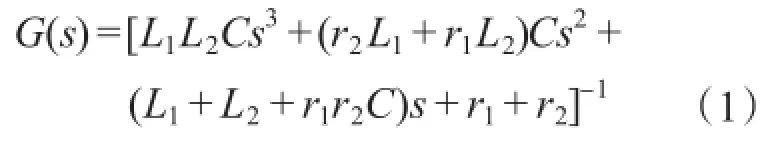
若不考虑等效寄生参数的影响:

由式(2)可知,LCL型滤波器是3阶系统,增大了谐振频率处谐波的幅值,致使系统总谐波畸变率(THD)增加。谐振频率为

2 系统总体结构设计
本文中并网逆变器的输入方式选择电压源输入,输出控制模式选择电流控制,逆变器输出经LCL滤波器滤波后并入电网。针对LCL滤波器的谐振问题,目前提出了增加系统阻尼的2种方案:无源阻尼法和有源阻尼法[6]。有源阻尼法通过反馈控制增加系统阻尼,没有损耗,是目前并网电流控制研究的主流,因此本文提出一种内环采用比例控制器控制电容电流、外环采用模糊PR+重复控制器控制并网电流的并网电流新型双环控制策略。系统的总体结构如图2所示。
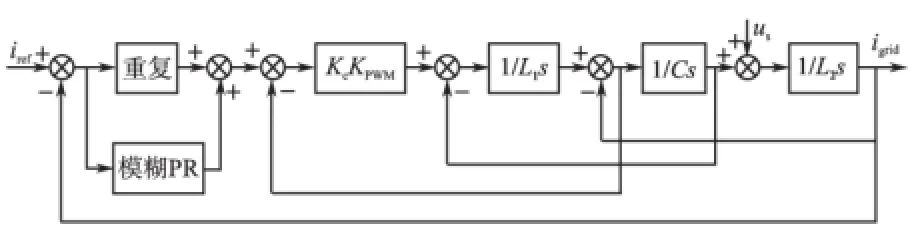
图2 控制系统结构Fig.2 Control system structure
图2中,Kc是电容电流反馈系数,内环采用有源阻尼法反馈电容电流,抑制高频谐振[7];外环通过引入重复+模糊PR新型复合控制器对并网电流实现跟踪,新型复合控制器由重复控制器和模糊PR控制器并联而成。其中重复控制对周期性干扰有良好的抑制作用;PR控制实现了对并网电流的无静差控制,且不受电网电压干扰,因此无需引入电网电压前馈控制。模糊控制对PR控制器参数实时在线整定,减小了外界干扰和参数变化对系统的影响。LCL滤波器在引入电容电流反馈后的传递函数应改为[8]
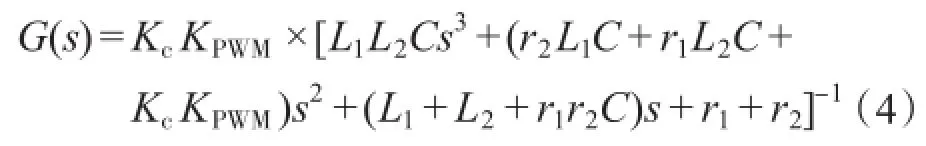
若不计等效寄生参数的影响:

其中
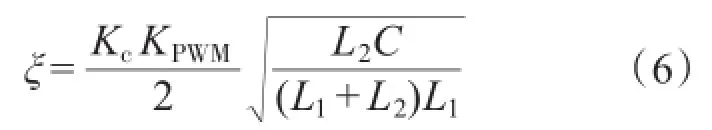
式中:ξ为期望的阻尼比;ωn为系统期望的自然频率;KPWM为SPWM逆变单元增益环节;Kc为电容电流反馈系数。
由文献[4]中伯德图可知,系统在电容电流反馈引入后,增加了系统的阻尼,较好地抑制LCL滤波器的谐振尖峰,改善了系统的稳定性。
3 控制器设计
3.1 PR控制
针对传统PI控制无法较好地实现对参考信号无静差跟踪,因此采用PR控制,即比例谐振控制,由比例项和谐振项构成。其传递函数如下:
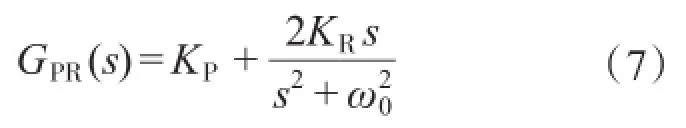
式中:ω0为谐振角频率;KP为比例项系数;KR为谐振项系数。
本文中,电网频率设定为50 Hz,则谐振角频率ω0=2×50×π=314 rad/s。PR控制器在基波频率处的增益为
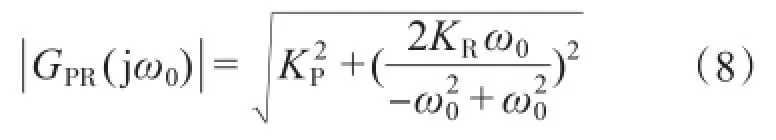
PR和PI控制器的伯德图如图3所示。
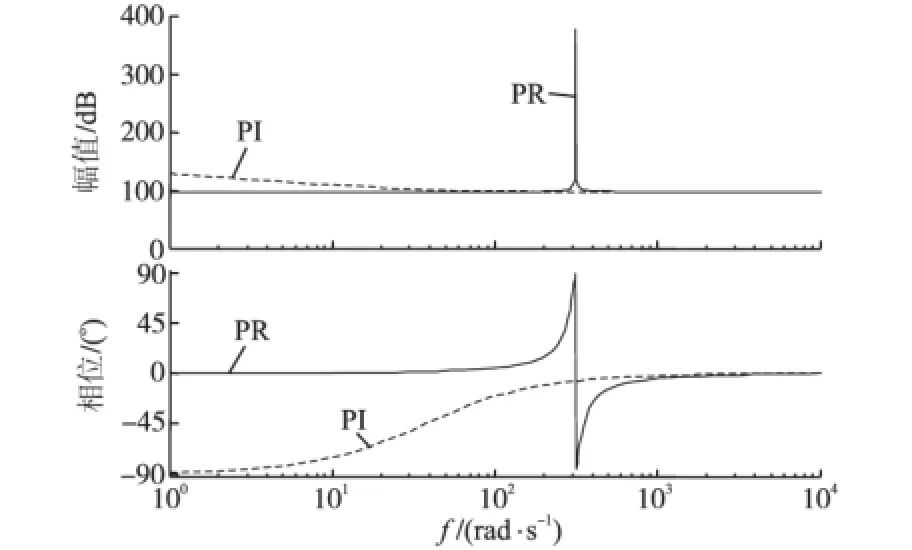
图3 PR和PI控制器Bode图(Kp=0.8Kr=Ki=30)Fig.3 The bode of PR and PI control

式中:N为1个周期内采样次数,若电网基波频率为50 Hz,采样频率为10 kHz,则周期采样次数N=200;z-N为周期延迟环节;Q(z)为积分衰减系数,一般为小于1的常数,通常取经验值0.95;Gc(z)为补偿器。
Gc(z)根据控制对象而设计,是重复控制器最重要的部分,可以改善电流波形质量,重复控制系统框图如图4所示。
由图3可知,由于控制器传递函数的jω轴上加入2个开环极点,形成该频率下的谐振,使得PR控制器在基波频率处的增益趋于无穷大,可以实现对某一频率正弦指令信号的无静差跟踪控制。因此PR控制器与PI控制器相比,能够消除相位误差,具有更好的稳态性能。此外,PR控制不受电网电压干扰的影响,无需加入网压前馈。
3.2 重复控制
PR控制器虽然对控制并网电流有良好的稳态性能,但对于电网电压及开关器件产生的周期性扰动并没有较为显著的改善效果。针对此问题,文献[9]提出了一种基于内膜的控制方法:重复控制,其对周期性扰动具有良好的抑制能力。重复控制系统的离散数学模型为
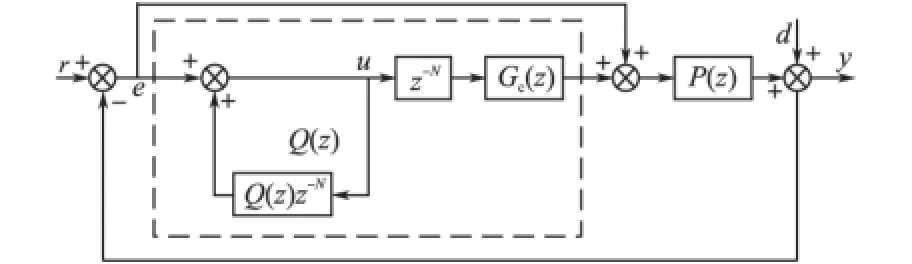
图4 重复控制系统Fig.4 Repeat control system
图4中,d为周期性扰动;r为正弦信号;y是逆变器输出电压;P(z)为控制对象,在并网系统中为空载逆变器传递函数;补偿器表达式为Gc(z)=Kr×zk×S(z),其中,Kr为重复控制增益,常用于补偿幅值,在单相并网系统中通常取小于1或等于1的常数;k为超前环节,一般取正整数;S(z)为重复控制器的滤波器。设计过程如下。
1)确定被控对象数学模型。对于LCL型并网逆变器的3阶系统而言,可以采用,2阶系统对其动态性能进行近似分析,因此文献[10]提出采用极点配置估算高阶系统性能,配置理想极点为
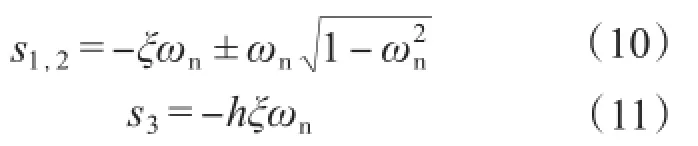
式中:ξ为期望的阻尼比;ωn为系统期望的自然频率;h为常数,h的取值反映了2阶系统等效3阶系统动态性能的近似程度,h=4。
将LCL滤波器参数L1=5 mH,L2=2 mH,C= 15µF代入式(3),可得LCL型逆变器系统的谐振频率为6 831 rad/s,取ωn=6 500 rad/s。由于阻尼比在0.707时系统有较好的动态性能,取阻尼比ξ=0.7,将参数代入式(10)、式(11),系统期望的极点为:s1,2=4 550±3 560j,s3=-18 200,由式(4)知,系统无零点,故系统被控对象为
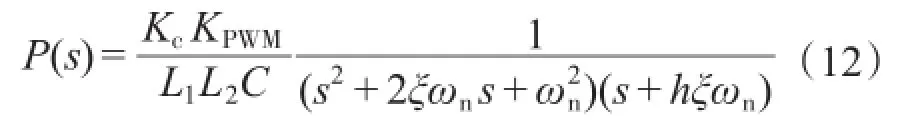
文中采样频率为10 kHz,采样周期为0.000 1s,将参数代入式(12),离散化可得:
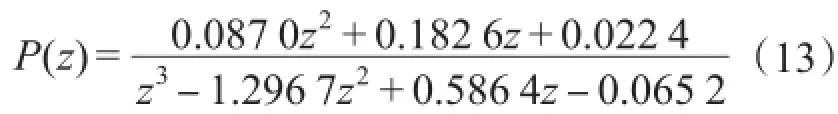
2)确定重复控制增益。控制增益Kr主要是提供幅值补偿,根据开环谐振峰值,取Kr=1较合适。
3)滤波器设计。设计为S(z)为2阶低通滤波器。由于电容电流反馈已滤除了被控对象的谐振峰值,故无需引入陷波器。陷波器在高频谐波抑制能力较弱,引入1个2阶低通滤波器,截止频率选取6 500 rad/s,阻尼系数0.7,有:
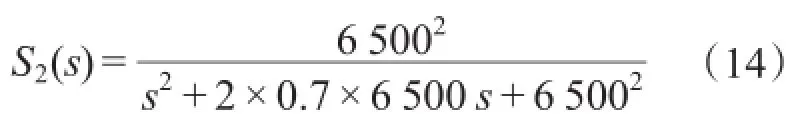
离散化可得:

4)超前环节k确定。
图5为系统加入重复控制前后的对比伯德图。由图5可知,重复控制系统存在相位滞后,利用超前环节zk补偿,超前环节作为相位补偿环节以补偿由逆变器控制对象P(z)和滤波器S(z)所引入的总相位滞后,在中低频段超前环节能实现较好的相位补偿[11],本文选取k=5。由图5可知,系统在采用重复控制后中低频段增益稳定且频率范围较宽、高频段衰减快速,具有良好的稳定性和鲁棒性。

图5 电流控制系统波特图Fig.5 Bode figure of current control system
3.3 模糊PR控制
模糊PR控制原理是:根据逆变器的数学模型,确定PR控制参数的初始值KP0和KR0。模糊控制器的输入为指令电流iref和并网电流igrid的误差e与误差de,输出为对PR控制参数KP和KR的改变量ΔKP和ΔKR,系统的模糊PR控制框图如图6所示。模糊规则根据KP和KR的控制作用来制定。
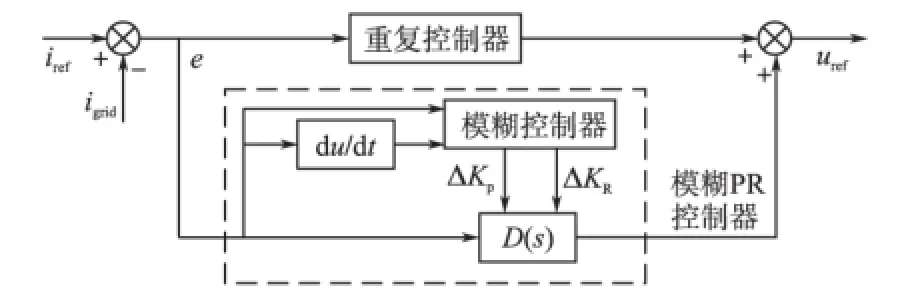
图6 模糊PR控制框图Fig.6 Fuzzy PR control system
图6中,KP为比例系数,影响系统比例增益,增大其值可以加快系统响应速度,提高精度,但是会增大系统超调量。KR为谐振系数,影响系统谐振峰值和带宽,增大其值可以减小系统稳态误差,起着和积分系数相似的作用。以控制KP为例:当系统误差与误差变化率处于较大级别并且变化方向相同时,增大KP以增强控制器的调节作用;反之,减小KP避免超调或者振荡;当系统趋于稳定且误差较小时,为保持系统稳态应适当减小KP。控制规则如表1所示。以KP为例,解模糊后的控制量为
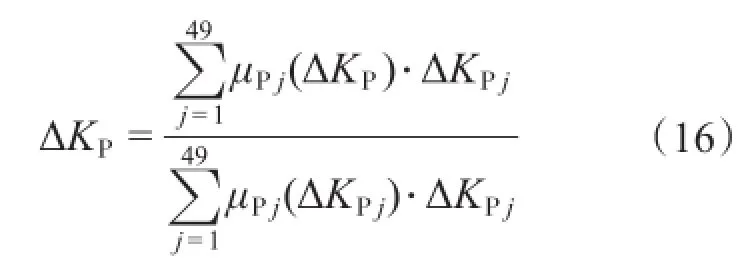
修改后的KP为

式中:K为比例因子。

表1 Δ KP和ΔKR的模糊控制规则Tab.1 The fuzzy control rule table of ΔKPand ΔKR
4 仿真结果分析
根据前述分析,本文在Matlab中建立了仿真模型并进行分析。新型复合控制同PR控制和重复控制仿真波形如图7所示。

图7 并网电流电压波形及3种控制方案下的THD值Fig.7 Grid connected current and voltage waveforms and THD values under three control schemes
本文中仿真时间为0.1 s,指令电流为30 A。其它仿真参数为:电网电压220 V,直流电压400 V,电网频率50 Hz,开关频率10 kHz,电感L1=5 mH,KP0=0.8,电容C=15µF,KR0=30,电感L2= 2 mH,Kc=0.12。
从图7中可以看出,新型复合控制下网侧电压和电流基本同相位,实现了单位功率因数并网的目标。同时可以看出,在稳态条件下,基于重复PR控制下的并网电流THD为1.52%,幅值为29.83 A,与指令电流相差0.17 A,达到并网标准,但是效果并不是很好。在新型复合控制条件下,并网电流THD为0.88%,该控制策略下的电流THD降低很多,幅值为29.9 A,与指令电流相差0.1 A,稳态电流质量效果明显提高,证实本文所提方法的可行性和优越性。
同时,本文还对系统的动态性能进行了验证。设定指令电流在时间0.035 s(波谷)从30 A跳变到40 A,重复PR控制和新型复合控制并网电流跟踪情况分别如图8、图9所示。
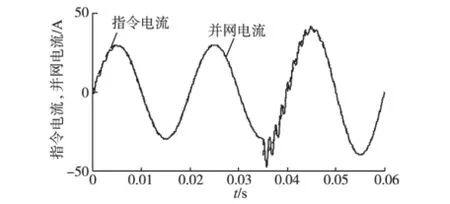
图8 指令电流突变重复PR控制并网电流波形Fig.8 The grid-connected current waveforms of the repeat PR control when the instruction current changes
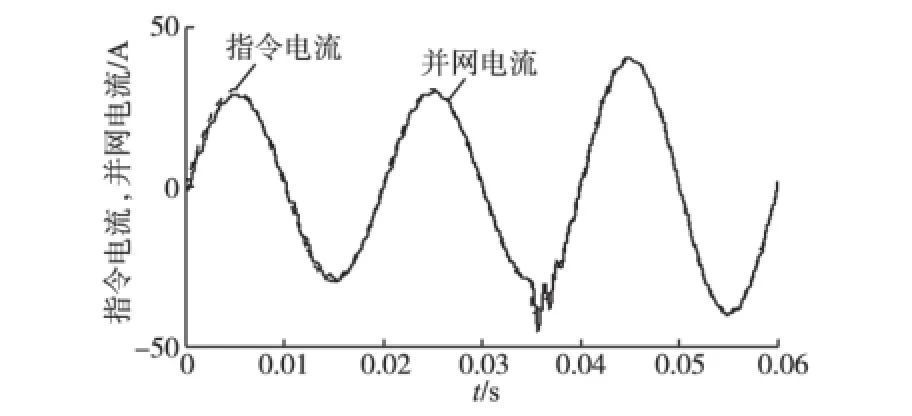
图9 指令电流突变新型复合控制并网电流波形Fig.9 The grid-connected current waveforms of the new compound control when the instruction current changes
由图8、图9可知,在0.035 s新型控制并网电流波动小于重复PR控制。同时,重复PR控制并网电流跟踪上指令电流约需0.01 s,而新型控制并网电流在0.003 s后可以跟踪上指令电流,使系统稳定,提高了系统的动态性能。
5 结论
针对单相LCL并网逆变器并网,本文研究了基于模糊PR控制和重复控制的一种新型电流双闭环控制策略。在理论分析的基础上进行了仿真研究,验证了以下结论:
1)新型复合控制下网侧电压和电流基本同相位,实现单位功率因数并网。并将其与已有的控制策略,即重复PR控制相比较。在系统稳态时,新型复合控制具有较低的电流谐波畸变率和较小的电流幅值误差,证明新型复合控制具有较高的稳态电流质量;
2)对于负载变化的单相LCL并网逆变器,新型复合控制策略有良好的动态响应,可以较好地抑制负载变化对并网电流的影响,提高了系统的动态性能。
[1]杭丽君,李宾,黄龙,等.一种可再生能源并网逆变器的多谐振PR电流控制技术[J].中国电机工程学报,2012,32(12):51-58.
[2]Mariethoz S,Morari M.Explicit Model-predictive Control of a PWM Inverter with an LCL Filter[J].IEEE Trans.on Industrial Electronics,2009,56(2):389-399.
[3]王斯然,吕征宇.LCL型并网逆变器中重复控制方法研究[J].中国电机工程学报,2010,30(27):69-75.
[4]黄挚雄,徐保友,沈玲菲,等.LCL并网逆变器新型电流双环控制策略研究[J].电力系统保护与控制,2012,40(17):1-5.
[5]刘飞,查晓明,段善旭.三相并网逆变器LCL滤波器的参数设计与研究[J].电工技术学报,2010,25(3):110-116.
[6]王学华,阮新波,刘尚伟.抑制电网背景谐波影响的并网逆变器控制策略[J].中国电机工程学报,2011,31(6):7-14.
[7]Liserre M,Blaabjerg F,Hansen S.Design and Control of an LCL-filter Based Three-phase Active Rectifier[C]//Thirty-sixth IAS Annual Meeting Conference Record of the 2011 IEEE,Hyatt Regency Hotel.Chicago,USA.2011.
[8]王要强,吴凤江,孙力,等.带LCL输出滤波器的并网逆变器控制策略研究[J].中国电机工程学报,2011,31(12):34-39.
[9]Shen Guoqiao,Zhu Xuancai,Zhang Jun,et al.A New Feedback Method for PR Current Control of LCL-filter-based Grid-connected Iinverter[J].IEEE Trans.on Power Electronic 2010,57(6):2033-2041.
[10]许津铭,谢少军,唐婷.基于极点配置的LCL滤波并网逆变电流控制策略[J].电力系统自动化,2014,38(3):95-100.
[11]张娜.基于重复控制理论的光伏并网逆变器输出控制的研究[D].天津:天津大学,2010.
Research on New Current Control Strategy of Single Phase LCL Grid-connected Inverter
YANG Xuhong,WANG Chuangdian,HE Chaojie,LI Haoran,WANG Yizhou
(School of Automation Engineering,Shanghai University of Electrical Power,Shanghai200090,China)
LCL-type grid-connected inverter is a three-order multivariable systems,grid connected current single loop control is difficult to meet the stability of the system.A new double-loop control strategy which the inner-loop used capacitor current feedback and the outer-loop adopted grid-connected current feedback was proposed.The inner-loop used proportional regulation to increase the system damping,to suppress high frequency resonance problems;the outer-loop adopted fuzzy PR+repeat control to adjust the influence of system interference on-line,to achieve high power quality network of the system.Simulation and experiment results demonstrate the feasibility of the proposed control system,and compare with PR control and DR control combined with repetitive control to prove that the control method has good stability and robustness.
filter;grid-connected inverter;repetitive control;fuzzy and proportional resonant control
TM615
A
10.19457/j.1001-2095.20161211
2015-11-04
修改稿日期:2016-06-20
上海市电站自动化技术重点实验室开放课题(13DZ2273800);上海市科技创新行动技术高新技术领域重点项目(14511101200);上海市重点科技攻关计划(上海市科委地方院校能力建设项目)(14110500700);国家自然科学基金(61203224);上海自然科学基金(13ZR1417800)
杨旭红(1969-),女,教授,硕士生导师,Email:yangxuhong.sh@163.com

