基于模型的大型曲面外形检测与评定

郑成成，杜福洲

（北京航空航天大学 机械工程及自动化学院，北京 100191）

检测与监控

基于模型的大型曲面外形检测与评定

郑成成，杜福洲

（北京航空航天大学 机械工程及自动化学院，北京 100191）

针对大尺度产品曲面外形检测效率低、精度与评定一致性差等问题，提出了基于模型的曲面外形检测与评定方法。针对飞机蒙皮外形检测，在分析大型曲面检测要求的基础上提出“双截平面法”的布点策略，基于隔框位置在蒙皮CAD模型上进行测点布局与检测路径规划。以激光跟踪仪测量结果作为数据支持，提出基于模型的“点-线-面”曲面综合评定方法：基于点的误差分布可视化反映蒙皮上各点的误差分布情况；线轮廓度反映蒙皮在隔框上的装配质量，是保证飞机外形准确度的关键；面轮廓度反映飞机蒙皮总体装配质量。基于模型的曲面外形检测与评定可快速地对蒙皮模型进行测点布局与路径规划，并能精确地评价蒙皮装配质量。

测点布局；路径规划；线轮廓度；面轮廓度

0 引言

蒙皮是构成飞机气动力外形的重要部件，对装配后的外形准确度有着严格的要求。蒙皮与隔框结构在航空航天、船舶等行业有着广泛的应用，随着测量技术的不断提升，对蒙皮外形测量要求也提出更高的标准。传统蒙皮外形检测采用样板采样法和打点采样法[1]，测量效率低、数据精度差，无法满足曲面高精度的外形评定要求。目前曲面外形检测方法有接触测量法、激光扫描法和视觉法[2]等，其中激光跟踪仪以测量精度高、操作便捷和适合大尺寸工件测量得到广泛应用，属于接触式测量法。本文结合激光跟踪仪测量特点，对蒙皮曲面进行测点布局、路径规划以及曲面综合评定。

基于离散点的蒙皮曲面综合评定的数据基础为测点布局生成的测量点云，因此曲面测点布局会影响曲面综合评定的准确性。基于激光跟踪仪测量路径规划的目的在于保证靶标可见性原则的前提下，以最短的路径遍历所有的测量点。合理、有效地测点布局和路径规划方法将提高曲面外形评定的效率与精度。侯尚等[3]运用曲面（U，V）特征来进行测点布局并提出了矩形合并测量路径规划方法；Li[4]提出基于曲率测度自适应采样规划方法；黄光胜[5]等运用“截平面”法对复合材料构件规划“弓”字形的检测路径。

蒙皮固定在隔框上，保证蒙皮在隔框上的装配质量是保证蒙皮外形准确度的关键，采用线轮廓度反映蒙皮在隔框上的装配质量。面轮廓度是曲面评定最常用的一种方法，基于离散点的面轮廓度评定主要是反映实测点云与测量点云之间的偏离程度，反映整个曲面的装配质量。基于模型的误差分布可视化结合模型图形和数据直观展现实测点相对理论曲面的误差分布情况与内在联系。张松[6]针对复杂曲面应用ICP法和投影法分进行曲面误差评定。蔺小军[7]等针对航空发动机叶片提出了根据叶型面轮廓度误差评定叶片型面精度的方法。戴能云[8]等提出了基于分割逼近法与MATLAB向结合的线轮廓度评定方法。张进[9]等提出了一种基于离散点的线轮廓度评定方法。合理、全面的评定曲面的装配质量，可为装配过程提供理论依据，完善工艺规程，形成闭环控制。

综上所述，本文针对装配后的飞机蒙皮外形检测效率低、精度差等问题，在理论模型上进行测点布局和路径规划，并对蒙皮外形进行基于模型的“点-线-面”的综合评定。

1 曲面测点布局和路径规划

1.1 工件坐标系的建立

工件坐标系的创建是为了将曲面的布点规则由模型坐标系转化到工件坐标系中，方便布点规则的建立。采用三点法和右手坐标系原理建立工件坐标系，如图1所示，选取P1点作为坐标原点，P1、P2连线作为坐标系X轴方向，右手坐标系确定Z轴与Y轴方向，原点及各轴系的确定公式如下：

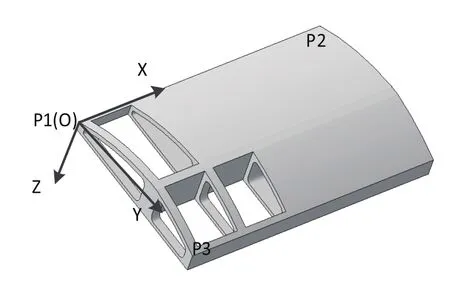
图1 创建工件坐标系

1.2 测点布局

蒙皮固定在隔框上，保证蒙皮在隔框上的装配质量是保证蒙皮外形准确度的关键，因此测点布局需要与隔框位置相对应。截面线[10]的基本思路是采用一组平行平面或一组曲面去切割曲面，得到一系列的交线。基于截面线法的思想提出“双截平面法”布点规则即采用两组相互垂直的平面切割曲面，得到一系列的交点。如图2所示，将截面分为主截面AOB1和辅截面AOB2，主截面通过隔框，截面的法向量n与工件坐标系的轴系平行。第一次进行曲面切割的截面称为主截面，主截面AOB1切割曲面边线得到两个交点E1和 E2，连接两点得到直线段然后对曲面进行辅截面切割，辅截面AOB2与直线段相交得到位于曲面外的交点M，将点M向曲面投影，若投影点位于曲面上则得到测量点P。对曲面进行多组双截面切割，可得到一系列分布在主截面两侧的测量点，根据截面与工件坐标系原点O之间的距离d设置满足不同要求的截面来满足不同的测量需求。当所有截面之间的距离相同时实现均匀布点，也可根据设置不同的d值，实现适应性布点。

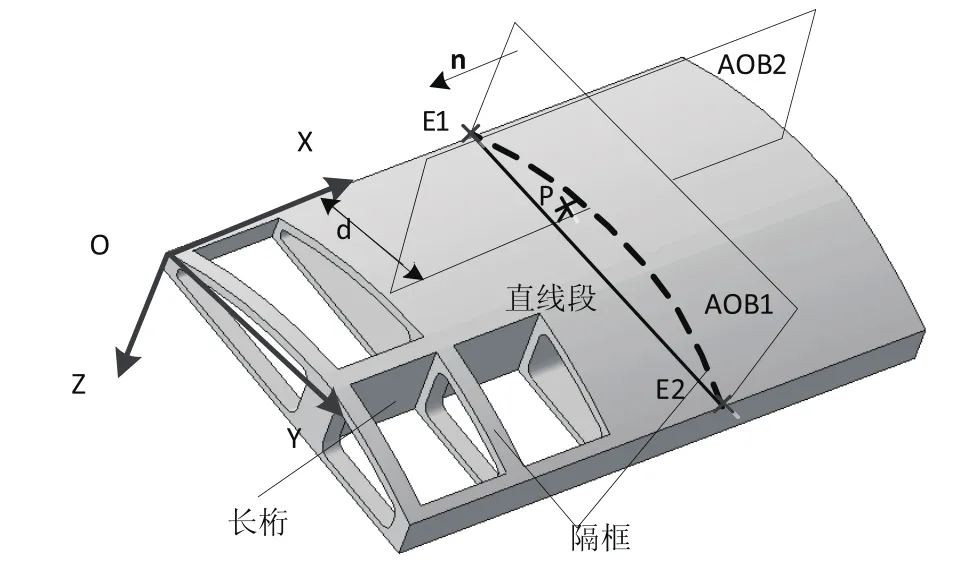
图2 双截平面法布点规则

1.3 路径规划

测点布局所生成的测量点P包含(x,y,z,i,j,k)等信息，(x,y,z)描述测量点在工件坐标系下的空间位置信息，(i,j,k)描述测量点在曲面上的法失信息。激光跟踪仪通过实时监测靶球位置状态来获取靶球中心接收器的空间位置信息，无法直接测量曲面上的测量点，因此需要对测量点P沿其法失方向偏移到靶球半径处生成偏置测量点P'(x',y',z',i,j,k)。沿主截面方向由下而上依次连接测量点P和偏置测量点P'形成“锯齿形往返式”的检测路径，如图3所示，通过合理的布站，来保证靶标可见性原则，使激光跟踪仪可以对所有的偏置测量点进行测量且不存在干涉问题。此时的测量点与偏置测量点的位置信息只具有工件坐标系的坐标属性，为了方便测量需要将测量点和偏置测量点的空间位置信息转化到模型坐标系下。

图3 双截平面法下的检测路径规划策略

2 基于模型的曲面外形评定

2.1 基于模型的线轮廓度评定

按照最小区域法评定线轮廓度误差是指包容被测轮廓的理论轮廓等距线距离为最小[8]。通过半径补偿、三维数据预处理、坐标系对齐和平面曲线位姿调整使包容被测曲线的理论曲线等距线距离为最小。线轮廓度公差数学模型描述如下：

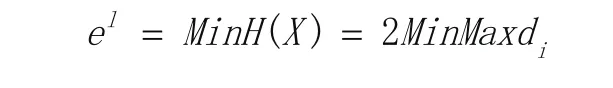
式中，H(X)包容被测曲线的理论曲线等距线距离，di为被测曲线上的点距离理论曲线的最小距离。

如图4所示，实测点Q位于被测曲线外，实测点Q到理论曲线的最小距离为r'不能表示理论曲线与被测曲线之间的变动量，而应由理论实测点L到理论曲线的最小距离r表示。r'与r存在一一对应关系，这种关系受被测曲线各点的法失方向影响，难以明确被测曲面各点的法失方向，但实测点Q可用理论实测点L沿其法失方向偏移靶球半径R表示。将被测曲线与理论曲线上所有点沿其法失法向偏移靶球半径形成被测靶球中心轨迹曲线和理论靶球中心轨迹曲线。用理论靶球中心轨迹曲线[11]代替理论曲线进行半径补偿，将理论曲线与被测曲线的关系转化到理论靶球中心轨迹曲线与被测靶球中心轨迹球曲线上。

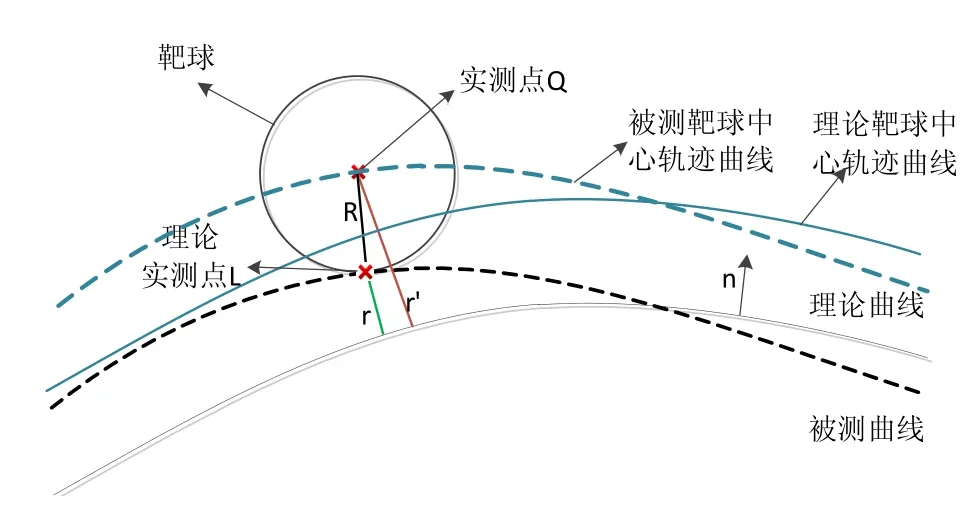
图4 靶球半径补偿示意图

基于模型的测点布局所生成的测量点分布在主截平面两侧，而且在测量过程中由于靶球放置有细微偏差，导致理论点与实测点不在同一平面内。本文采用向主截平面投影的方法来保证理论点与实测点位于同一平面上，并保留与主截平面相互平行的坐标轴系信息，将点云坐标信息由三维转化为二维。投影会导致理论点与实测点对相对位置的失真，引入投影误差。为避免投影误差过大对最终结果产生较大影响，需进行投影误差补偿，如图5所示，实测点Q和理论点P经过向主截平面投影得到平面实测点Q'和平面理论点P'，沿向量Q'P'方向将平面实测点Q'偏移至偏移点C处，偏移距离为投影失真量d-d'，进行误差补偿。为方便描述，线轮廓度评定过程中将平面理论点P'视为理论点，偏移点C视为实测点。

坐标系对齐将模型坐标系与激光跟踪仪测量坐标系对齐，避免因坐标系不同引入的误差。

曲线位姿调整是将被测曲线通过旋转与平移操作使其无限接近理论靶球中心轨迹曲线的过程。采用最小二乘法代替“最小包容区域”原则来评定线轮廓度误差，通过最小二乘法计算出两组点云之间的距离平方和，求解最佳匹配信息。最小二乘法下理论点集与实测点集之间的位姿变换矩阵可描述为：

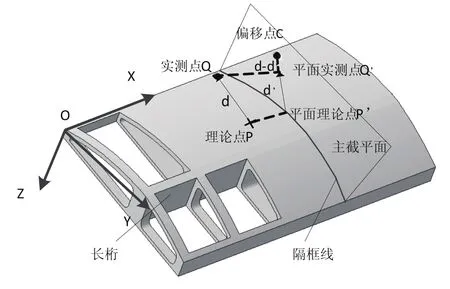
图5 实测点与理论点的投影误差补偿

式中，R为实测点云到理论点云的旋转矩阵，T为实测点云到理论点云的平移矩阵，ωi为点云中每个点对的权重，pi为理论点云，qi为实测点云。

通过SVD奇异值分解算法解算出旋转矩阵R、平移矩阵T，令实测点云通过位姿调整与理论点云最佳匹配，在最小二乘的原则下满足“最小包容区域”要求。

线轮廓度误差e1可用实测点qi至理论曲线1(x,y,z)的最小距离di中的最大值来表示。将理论点云通过B-Spline曲线拟合的方法拟合成理论曲线1(x,y,z)。

基于模型的点到曲线的最小距离求解可转化为点到曲线投影问题。将所有实测点向理论曲线投影，最大投影值的两倍便是线轮廓度误差。

2.2 基于模型的面轮廓度评定

面轮廓度公差带为球心位于理论曲面上且被测曲面被完全包含在最小偏差为±r所在的区域。无基准的面轮廓度误差评定需要满足“最小包容区域”原则，即通过半径补偿、坐标系对齐和曲面位姿调整使被测曲面与理论曲面的最大变动量为最小，面轮廓度误差em的数学模型描述如下：

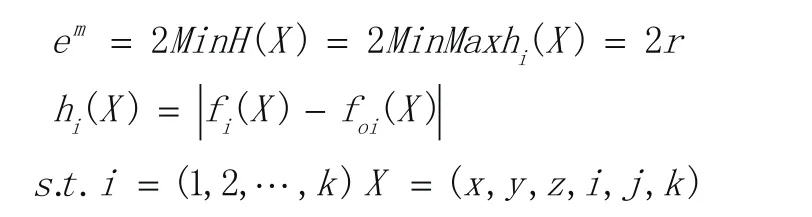
式中，H(X)为被测曲面与理论曲面的最大变动量，hi(x)为被测曲面与理论曲面的变动量，fi(x)为被测曲面空间位置姿态函数，foi(x)为理论曲面的空间位置姿态函数。

由最大变动量为最小的数学模型知，求解面轮廓度误差关键在于解算被测曲面与理论曲面的变动量，即计算实测点距离理论曲面的最小距离r。

采用线轮廓度误差半径补偿的方法，通过偏置测量点云代替理论点云，构建理论靶球中心轨迹曲面代替理论曲面进行半径补偿。基于CATIA平台使用曲面偏移功能构造理论靶球中心轨迹曲面。

通过激光跟踪仪转站可实现激光跟踪仪测量坐标系和模型坐标系的对齐。基于曲面测点布局得到的偏置测量点云和激光跟踪仪测量得到的实测点云，采用最小二乘法代替“最小包容区域”原则来评定面轮廓度误差，最小二乘法下位姿变换矩阵可描述为：

式中，R为实测点云到偏置测量点云的旋转矩阵，T为实测点云到偏置测量点云的平移矩阵，ωi为点云中每个点对的权重，pi为偏置测量点云，qi为实测点云。

因每个点对的权重相同，故ωi=1。当最大变动量为最小时需要满足两组点云之间的距离平方和最小，即令函数对R、T的偏导为0。使用SVD（奇异值分解）方法求解旋转矩阵R，进而求解平移矩阵T。实测点云和偏置测量点云可实现最佳匹配，在最小二乘的原则下满足“最小包容区域”要求。此时面轮廓度误差em可用实测点qi至理论靶球球心轨迹曲面u(x,y,z)的最小距离di中的最大值来表示。

基于模型的点到曲面的最小距离求解可转化为点到曲面投影问题。将所有实测点向理论靶球球心轨迹曲面投影，最大投影值的两倍便是面轮廓度误差值。

3 数据分析

基于模型的大型曲面外形检测与评定方法适用于所有的曲面模型，采用如图6所示大型曲面模型进行测点布局和基于“点-线-面”的曲面综合评定。

图6 大型曲面模型

3.1 线轮廓度误差分析

采用偏置测量点云代替理论点云进行补偿。根据双截平面法布点规则在理论曲面上测点布局得到的偏置测量点云数据如表1所示。

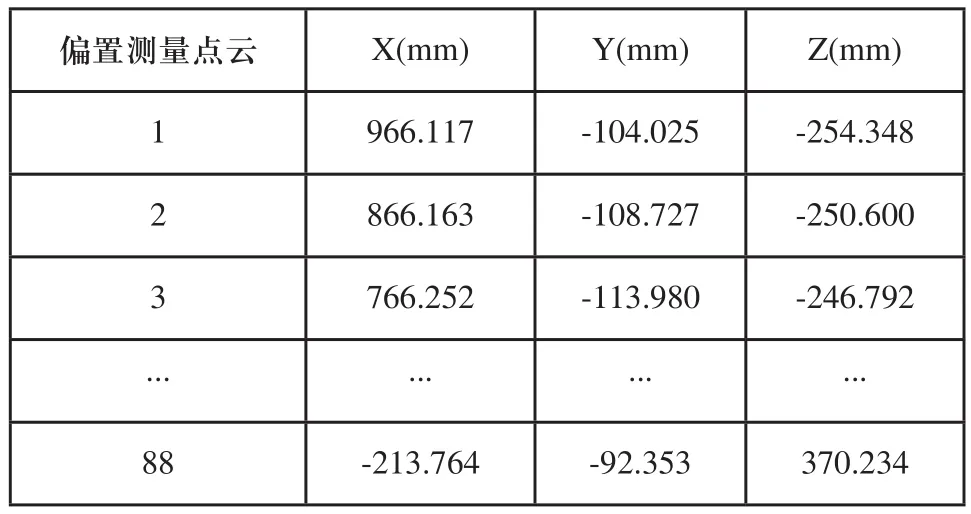
表1 偏置测量点云数据

添加均匀分布（-0.5，0.5）的布点与实测误差，基于随机函数生成的实测点云如表2所示。

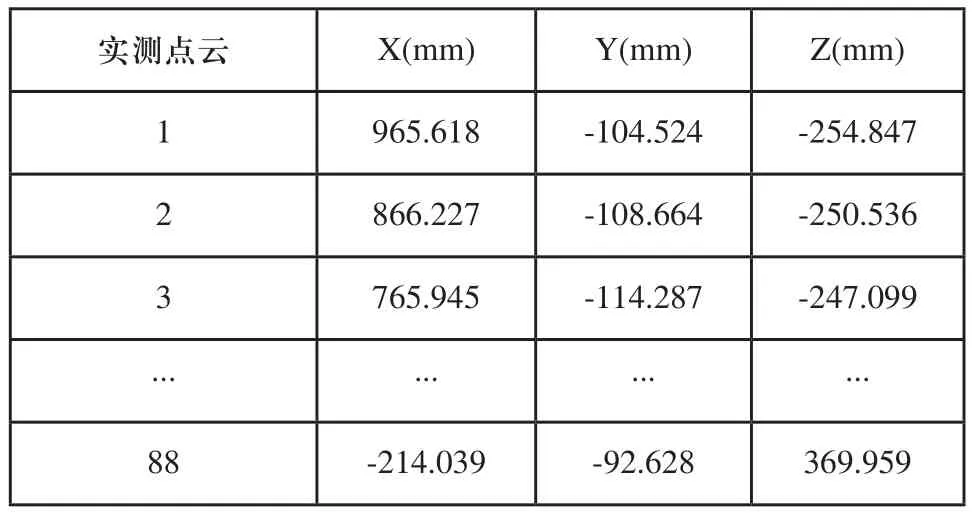
表2 实测点云数据

将基于双截平面法所布测点和实测点依据主截平面划分点组，如图所示将偏置测量点云与实测点云分为7组，如图7所示，作为线轮廓度评定的数据源。

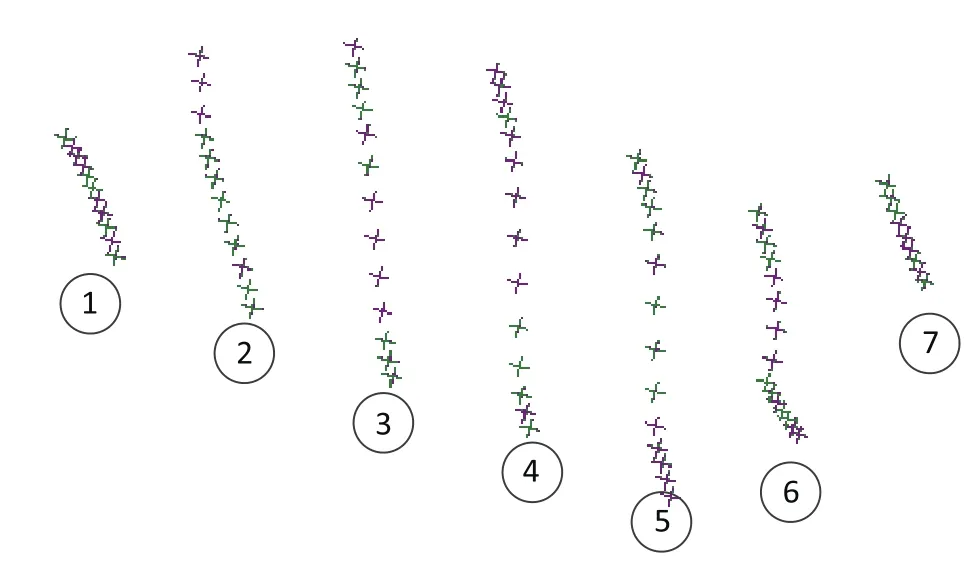
图7 点组划分

通过对数据进行投影误差补偿处理，使用SVD算法求解最佳匹配位姿矩阵使理论点云与实测点云达到最佳匹配，并使用B-Spline方法对理论点云拟合理论曲线。最后基于模型将实测点投影理论曲线上，求解线轮廓度误差，如图8所示。

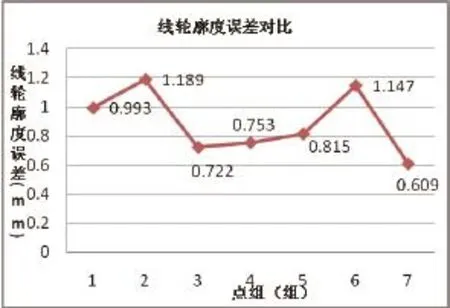
图8 各点组线轮廓度误差与对比

3.2 面轮廓度误差分析

采用最小二乘法代替“最小包容区域”原则来评定面轮廓度误差，通过SVD算法求得的位姿转化矩阵为：

实测点云经过位姿变化得到最佳匹配的点云数据如表3所示。

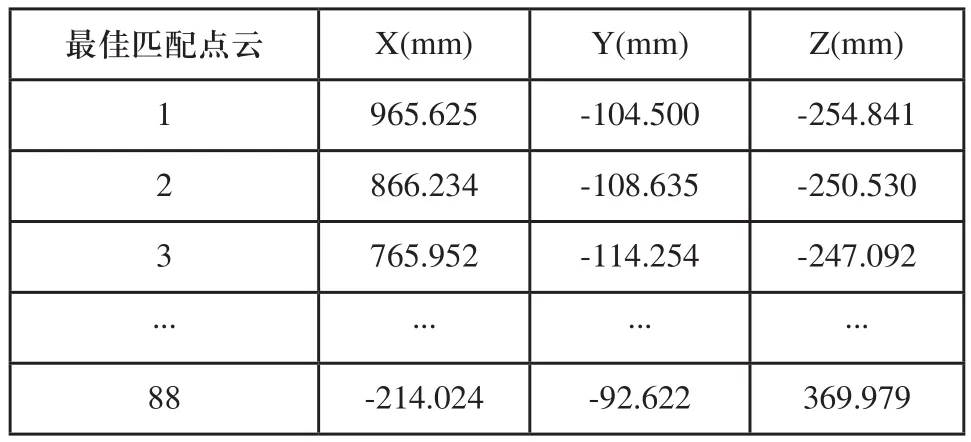
表3 最佳匹配点云数据

基于模型的面轮廓度误差评定可消除由点云拟合曲面所带来的误差，使面轮廓度误差求解更加精准。将最佳匹配的点云向理论靶球中心轨迹曲面投影得到的距离值作为点到曲面的最小距离计算面轮廓度，其误差分布如图9所示。其中误差最大值为0.591mm，面轮廓度误差为1.182mm。

图9 实测点的误差值

3.3 基于点的误差分布可视化

基于模型的误差分布可视化结合模型图形和数据直观展现实测点相对理论靶球中心轨迹曲面的误差分布情况与内在联系。利用CATIA三维建模的强大功能，创建由理论靶球中心轨迹球曲面垂直指向实测点的单向箭头，如图10所示，用箭头方向表示实测点相对于理论靶球中心轨迹曲面的位置与方向，用箭头颜色表示实测点所在不同的误差分层，并能交互式查看点到曲面的投影距离。

图10 基于点的误差分布可视化

4 结论

为精准检测飞机气动外形，本文提出了基于模型的曲面外形检测与评定方法，解决了大尺度产品曲面外形检测效率低、精度与评定一致性差等问题。

1）“双截平面法”的布点策略根据隔框位置设置主截平面，可保证生成的测量点与隔框相对应，是评价蒙皮装配质量的最好数据源。此布点策略同样适用于所有类型的曲面布点。

2）“锯齿形往返式”检测路径在保证靶标可见性原则的前提下，能够以最短的路径遍历所有的测量点。

3）在布点策略的支撑下进行线轮廓度评定，是蒙皮装配质量检验的关键指标，适用于飞机或船舶蒙皮装配质量的检验。

4）面轮廓度能够准确反映当前蒙皮装配的总体质量，适用于任何曲面的外形评价。

[1] 韩清华,郑保,等.采用激光跟踪仪测量飞机外形[J].航空计量技术,2004(24),15-33.

[2] 史恩秀,郭俊杰.大型薄板曲面件在即测量技术的研究[J].仪器仪表学报,2009(30),1795-1800.

[3] 侯尚,翟建军,黄翔,等.基于激光雷达的飞机外形检测路径规划研究[J].机械制造与自动化,2015(02),106-122.

[4] S Z Li，Adaptive Sampling and Mesh Generation, Computer-Aided Design,1995, 27(3): 235-240.

[5] 黄光胜,王美清,杜福洲,等.飞机复合材料构件超声C扫描检测轨迹规划系统研究[J].制造业自动化,2015(05),132-135.

[6] 张松.复杂曲面布点策略与误差评定方法研究[D].天津大学,2010(6).

[7] 蔺小军,单晨伟.航空发动顶级叶片型面三坐标测量机测量技术[J].计算机集成制造系统,2012(1),2281-2285.

[8] 戴能云,廖平,等.基于MATLAB的平面线轮廓度误差评定[J].光学精密工程,2008(11),125-131.

[9] 张进.离散点的线轮廓度评定算法[J].计算机测量与控制,2010(7),1590-1592.

[10] 李海滨.工程机械复杂零件加工刀具路径规划的研究[D].吉林大学,2011.

[11] 王建华,林其骏,乔桂芳.复杂型面测量中测头中心的轨迹曲面及测头半径的三维补偿[J].计量学报,1994(02),108-113.

图3 故障重调度之前的调度计划的资源-工序甘特图

7 结论

针对设备发生故障情况下的作业车间重调度问题，本文首先分析了重调度过程中涉及的主要动态约束条件；其次，确定了最小化作业延迟时间总量这一优化目标，完成了重调度问题的业务建模和数据建模；再次，采用混合集合规划理论和工具描述了重调度的主要约束、优化目标，设计了对应的求解算法；最后，利用某实际作业车间的生产数据对调度优化模型进行了求解和验证，求解结果表明了建模的合理性和求解的有效性。本文为设备故障情况下作业车间生产计划的重调度提供了一种可行的方法，有利于保证生产执行的稳定性、促进车间生产运行效率的提升。

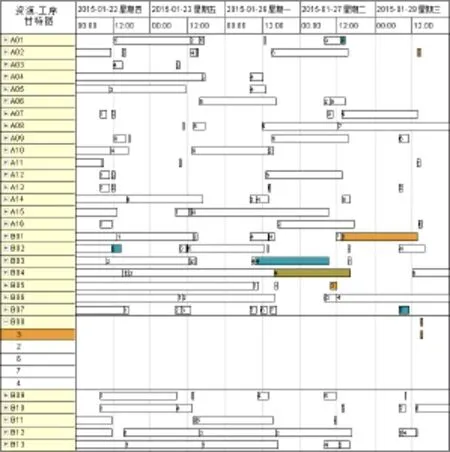
图4 故障重调度之后的调度计划的资源-工序甘特图

参考文献：

[1] 李春,葛茂根,张铭鑫,蒋增强.遗传粒子群算法的动态计划与排程问题研究[J].合肥工业大学学报(自然科学版).2010,33(1): 5-9.

[2] 刘爱军,杨育,邢青松,等.柔性作业车间多目标动态调度[J].计算机集成制造系统,2011,17(12):2629-2637.

[3] 王磊.基于改进离散粒子群算法的作业车间调度方法研究及应用[D].杭州:浙江工业大学,2012.

[4] Jianyang Zhou.A Note on Mixed Set Programming[J].The 7thInternational Symposium on Operations Research and ItsAppli cations,Lijiang,China,2008:131-140.

[5] 周建阳.自然约束语言[M].北京:科学出版社,2009.

[6] 倪骅,李照国.生产排程的混合集合规划算法[A].中国企业运筹学[2010(1)][C].2010:6.

[7] 杨龙,梅军,刘茂辉.基于混合集合规划的大规模生产排程算法的研究[A].中国企业运筹学[2011(1)][C].2011:8.

[8] 刘轩,尚鋆,白翱.基于混合集合规划的作业车间生产调度模型研究[J].制造业自动化,2015,37(12):39-43.

Detection and evaluation of large surface profile based on Model

ZHENG Cheng-cheng, DU Fu-zhou

TP302.1；V260.5

A

1009-0134(2016)12-0055-05

2016-08-15

国防基础科研项目（JCKY2013206C003，A2120132007）

郑成成（1992 -），男，山东临沂人，硕士研究生，研究方向为数字化装配、检测与评定。