含蓄电池的孤立微电网系统运行优化研究
褚衍廷, 董海鹰, 李晓青,2
(1.兰州交通大学 自动化与电气工程学院 甘肃 兰州 730070;2.兰州工业学院 电气工程学院 甘肃 兰州 730070)
含蓄电池的孤立微电网系统运行优化研究
褚衍廷1, 董海鹰1, 李晓青1,2
(1.兰州交通大学 自动化与电气工程学院 甘肃 兰州 730070;2.兰州工业学院 电气工程学院 甘肃 兰州 730070)
针对微电网系统在孤立运行方式下的优化问题,提出了一种含蓄电池的微电网多目标运行优化方法.求解方法分为2步:储能单元运行方式的确定及可控型微电源的优化调度.微电网储能单元的运行方式根据当前调度时刻的负荷需求、可再生能源发电期望、储能单元的荷电状态等因素,采用功率差控制策略对储能单元进行管理.可控型微电源的出力分配,在考虑系统功率平衡、微电源出力限值和爬坡约束等条件下,以经济成本和环境成本为目标,利用改进的遗传算法进行求解.该方法不仅发挥了蓄电池削峰填谷的作用,提高了储能单元的经济价值,而且实现了孤立微电网的经济、环保优化运行.以典型微电网系统的日优化调度为算例,验证了所提方法的可行性和有效性.
微电网; 孤网运行; 蓄电池; 运行优化
0 引言
微电网是一种新型能源网络化供应与管理技术,能够向用户提供可自主选择的供电方式,满足不同优化目标的用电需求,成为主网的有益补充[1-2].储能系统凭借其快速功率调节以及兼具供蓄能力的特征,在平滑间歇式能源功率波动、削峰填谷[3]以及提供备用电源等方面发挥了巨大作用[4],是微电网系统实现对接入的分布式能源灵活调节以及网络优化运行的关键所在.现阶段,微电网已经成为智能电网建设中的重要组成部分,对微电网优化控制等关键技术的研究已在国内外广泛开展[5-7].
针对并网运行模式下微电网的经济运行优化与调度研究,已经取得了一些研究成果[8-12],而孤立微电网运行优化研究尚处于起步阶段.然而在配电网故障或者无并网条件的偏远景区、孤岛等特殊情况,微电网只能孤立自治运行.文献[13]建立了集中控制模式下的微电网运行优化模型,文献[14]实现了微电网系统的动态经济调度,但均没有考虑储能单元.目前,考虑蓄电池对微电网运行优化影响的主流优化策略可分为固定策略[15-16]和动态策略[17-18].固定策略是在微电网运行优化时,对蓄电池采取事先拟定的调度规则,该调度规则不随自身情况和系统环境而改变,一般表现为蓄电池规律地反复充放电.动态策略是通过设计不同的蓄电池充放电罚系数,引导蓄电池能够跟随时段和环境的变化,实现不同情况下的运行控制.前者在应用中容易实现,但缺点也很明显,后者虽然能够在既定条件下实现最优效果,但在外部市场变化的情况下需做出相应调整.文献[19]在运用动态规划法确定储能单元运行方式的基础上,求解燃料电池运行方式,为确定微电网最佳运行方式提供了新思路,但此过程仅考虑了经济因素.因此,本文提出了一种含蓄电池的孤立微电网多目标优化调度方法,考虑了可再生能源出力的波动性、蓄电池的实时荷电状态以及负荷预测误差等因素,采用功率差控制策略确定蓄电池的运行方式,建立了微电网系统运行成本和环境成本的目标函数,利用改进的遗传算法求解各可控型微电源的出力分配,最终得到微电网系统整体的最优运行方式.通过典型微电网算例验证了所提方法的可行性和有效性.
1 微电网多目标运行优化模型
根据调度周期内总时段数的选取原则[20],选取调度周期为1 d,单位时间间隔为1 h来进行分析.在单位时间间隔内做如下假设:微电源的出力恒定和负荷的需求恒定.在此前提下,可认为分析计算时微电网为稳态运行,不考虑其暂态过程.
1.1 目标函数
风力发电和光伏发电均属可再生能源发电,不消耗燃料且不排放污染气体,本文忽略其运行成本,不把其出力作为优化变量.对于可控型微电源,由于本文针对运行时的优化调度,忽略其投资成本,考虑运行成本和环境成本,将其出力作为优化变量,微电网经济调度目标函数可表示为
minF(t)=min{F1(t),F2(t)},t=1,2,…,24,
(1)
式中:F1(t)为微电网运行成本;F2(t)为微电网环境成本.
目标1:微电网运行成本.
微电网运行成本可表示为
(2)
CM(Pi(t))=KOM,i·Pi(t),
(3)
式中:i为微电网中可控型微电源的编号;N为系统中分布式电源的数量;T为一个调度周期包含的时段数;Pi(t)为t时刻微电源i的输出功率;CF为可控型微电源的能耗成本;CM为可控型微电源的维护成本;KOM,i为微电源的运行维护系数.
目标2:微电网环境成本.
环境成本主要包括污染气体治理成本.因此,微电网环境成本可表示为

(4)
式中:m为污染物的类型;Vj为单位电量第j项污染物的治理费用;Qij为第i个微电源单位电量下第j项污染物的排放量.污染物的治理费用和排放系数如表1所示.
表1 污染物的治理费用和排放系数
Tab.1Externalitycostsandemissionfactors
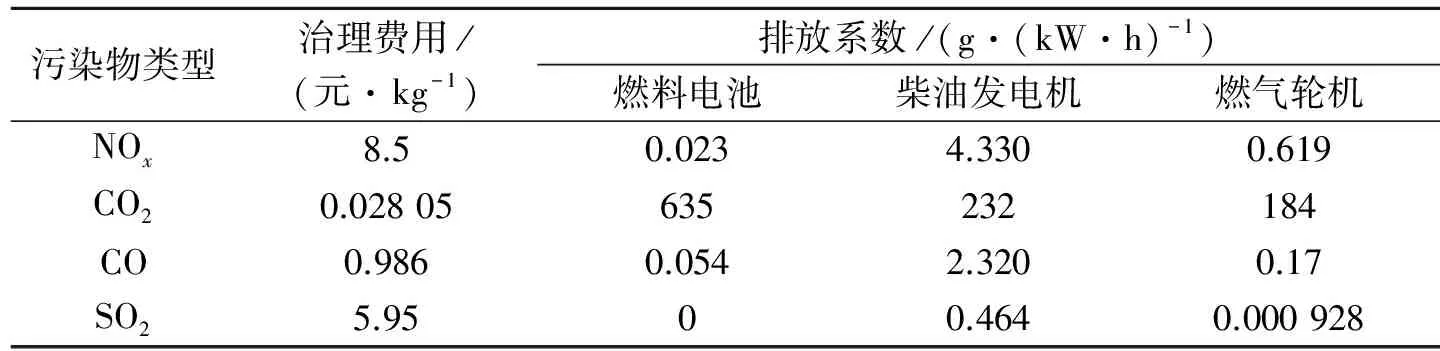
污染物类型治理费用/(元·kg-1)排放系数/(g·(kW·h)-1)燃料电池柴油发电机燃气轮机NOx8.50.0234.3300.619CO20.02805635232184CO0.9860.0542.3200.17SO25.9500.4640.000928
1.2 约束条件
1)功率平衡约束.
功率平衡约束为
(5)

2)有功出力约束.
有功出力约束为
(6)

3)可控机组爬坡约束.
增负荷时:
(7)
降负荷时:
(8)
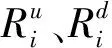

图1 多目标运行优化结构图Fig.1 Structure chart of multi-objective operation optimization
1.3 多目标运行优化流程
图1为含储能单元的孤立微电网系统多目标运行优化结构图,其中PBat为蓄电池的输出功率;PFC、PDE、PMT分别为燃料电池、柴油发电机、微型燃气轮机的输出功率.首先采用考虑实际约束的功率差控制策略确定蓄电池的运行方式,在此基础上再对各可控型微电源出力采用改进的遗传算法进行多目标优化调度,最终确定微电网的运行方式.
2 储能系统充放电控制策略
在微电网运行中储能装置发挥着削峰填谷和功率跟踪的作用,保证了微电网的安全可靠运行.利用电池储能系统的快速“吞吐特性”,负荷低谷期时储存能量待用,负荷高峰期时供应电能,实现削峰填谷,缓解了高峰期用电紧张,同时减少了可再生能源弃电现象的发生,实现各方面共赢[4].
储能系统根据预测的日负荷曲线制定充放电控制策略,即确定其在不同时段下的充放电功率大小.恒功率控制策略是储能系统最基本的充放电控制策略,即在任何时刻均以某一恒定的功率进行充放电.虽然计算简便,但是控制策略单一,对系统的响应效果差.本文采用考虑实际约束的功率差控制策略,解决了采用恒功率控制策略时,预测负荷与实际负荷由于峰、谷时间差造成控制策略失效的问题,并兼顾蓄电池容量、充放电功率以及荷电状态等约束,具体实现步骤如下:
1)根据已有负荷预测曲线,计算得到日负荷平均功率Pavg.
2)以Pavg为中心,ΔP为步长迭代,其中P1=Pavg+ΔP,P2=Pavg-ΔP,迭代过程满足如下约束条件:
(9)

(10)
Ec-Ed<ε,
(11)
式中:P2为储能系统充电功率上限值;P1为储能系统放电功率下限值;Pf、Pg为负荷峰、谷时间段的负荷值;E为电池储能系统容量;Ec表示总的充电能量;Ed表示总的放电能量;ε为接近于零的常数.当上述条件有一个无法满足时,重新返回迭代P1=Pavg+ΔP,P2=Pavg-ΔP,直到所有条件满足为止.
3)确定储能系统在具体时段的充放电功率.
当Pt>P1时,放电功率为
Pd=Pt-P1,
(12)
当Pt Pc=P2-Pt, (13) 式中:Pt为t时刻实测负荷值. 在实时控制时,倘若实际负荷曲线与预测负荷曲线出现偏移,该控制策略不会造成削峰填谷控制失策,能够根据实际情况调整储能系统的运行方式. 遗传算法是一种基于模拟自然选择和基因遗传学原理的并行优化搜索算法,能够解决复杂搜索空间的全局优化问题.遗传算法寻优性能由交叉概率Pc和变异概率Pm决定.Pc决定新个体产生的速度.Pc过小,搜索进度缓慢;Pc过大,遗传模式被破坏的可能性增大.Pm决定遗传算法跳出局部最优的能力.Pm过小,新的个体结构不容易产生;Pm过大,变成了随机搜索算法[15].在使用基本遗传算法的基础上,采用文献[15]改进后的Pc和Pm,可表示为 (14) (15) 式中:favg、fmax和fmin分别为种群中的平均、最大和最小适应度;f′为要交叉的两个体中较大的适应度,取Pc1=0.85,Pc2=0.5,Pc3=0.2,Pm1=0.09,Pm2=0.05,Pm3=0.01. 改进算法能够保证群体中适应度最大个体的Pc和Pm从0分别提高为Pc3和Pm3,使优良个体仍处于进化状态,从而使个体跳出局部最优解.当个体的适应度相比于平均适应度小时,适应度的值相对集中,使算法陷入局部最优解的概率增大,此时该改进能够增大Pc和Pm,从而增加种群的多样性. 在微电网系统多目标运行协调优化中,搜索空间中的每一个“染色体”都是优化问题的潜在可行解.定义目标函数F包括微电网1 d内的运行成本和环境成本,取目标函数的倒数为适应度函数,即f=1/F,优化变量为各可控型微电源的输出功率.对于微电源的运行约束条件(式(6)~(8)),体现为对于相应的优化变量数值大小的限制.若优化变量超过限值,则取其限值.对于功率平衡约束条件(式(5)),以罚函数的形式计入到目标函数中.运用改进自适应遗传算法,采取轮盘赌选择并执行多点交叉、多点变异操作求解算例.算法参数设置如下:种群规模为200,最大迭代次数为200. 选用图2所示的微电网系统结构[5,18,21],其中公共连接点保持断开,微电网孤立运行.系统中可再生能源有100 kW光伏电池和150 kW风机,可控型微电源包括微型燃气轮机、燃料电池和柴油发电机,储能单元为最大充放电功率50 kW、容量250 kW·h的蓄电池组.蓄电池的荷电状态为30%~90%.各分布式电源的相关信息如表2所示,可再生能源出力、日负荷和净负荷曲线如图3所示.由于负荷本身存在较大峰谷差及可再生能源出力的不稳定,净负荷会出现大幅度的功率波动. 表2 各分布式电源的相关信息 微电源类型功率/kW下限上限运行维护系数/(元·kW-1)最大爬坡率/(kW·h-1)上升率下降率燃料电池0650.0286140160微型燃气轮机0650.0401140160柴油发电机0800.0859120140 4.1 蓄电池在两种控制策略下的对比分析 对蓄电池采用恒功率控制策略进行求解,设定蓄电池充放电恒功率为30 kW,调整步长ΔP=0.1 kW,控制结果如图4所示.可以看出,釆用恒功率控制策略能够有效识别负荷峰期和谷期,且在单日内有一次充电和两次放电,但进一步分析可知,蓄电池出力与净负荷合成后不够平滑,存在新的峰谷差.如果预测负荷曲线和实际负荷曲线形状一致,仅负荷峰谷值不同,那么采用恒功率控制策略的蓄电池能够有效地实现削峰填谷.但是现阶段负荷的预测水平还不能达到理想水平,即如果预测负荷曲线与实际负荷曲线的峰、谷时间存在偏差时,那么此时恒功率控制策略将导致蓄电池在低谷期无法充电,高峰期不能放电,从而无法完成削峰填谷的任务. 图2 微电网系统结构Fig.2 Structure chart of microgrid system 图3 可再生能源出力、日负荷和净负荷曲线Fig.3 Daily output power of renewable energy, demand of load and payload 对蓄电池采用功率差控制策略进行求解,控制结果如图5所示.蓄电池在功率差控制策略下能够实现削峰填谷,且在单日内也有一次充电和两次放电,通过准确识别负荷的高峰期与低谷期,调整充放电动作.进一步分析可知,优化后的净负荷峰谷差值明显减小,负荷特性得到明显改善,不仅有利于微电网负荷侧的用电稳定,而且提高了微电网调度安全.此外,功率差控制策略是根据充放电功率上、下限值,确定蓄电池充放电工作域和功率值,若实测负荷曲线的峰、谷时间有偏差,该控制策略仍然能够准确控制蓄电池动作,并制定有效的运行方式.因此,采用功率差控制策略控制蓄电池的出力,并作为可控型微电源优化运行的基础. 图4 恒功率控制策略的控制结果Fig.4 Control results of constant power control strategy 图5 功率差控制策略的控制结果Fig.5 Control results of power difference control strategy 4.2 单目标优化结果 4.2.1 运行成本最小 优先使用采取跟踪控制最大功率输出的可再生能源机组的出力,以运行成本最小为目标的微电网运行优化结果如图6所示.可以看出,单从运行成本的角度考虑,由于燃料电池较微型燃气轮机低,微型燃气轮机又较柴油发电机低,在优先考虑运行成本最小的情况下,在燃料电池额定功率范围内,优先考虑燃料电池出力,超出额定功率后再考虑微型燃气轮机、柴油发电机出力.微型燃气轮机的发电效率与输出功率成正相关关系,当微型燃气轮机出力较小时,发电效率低,其运行成本增加,容易导致总运行成本增加,因此,微型燃气轮机出力时一般维持在较高水平,与图6优化结果相符. 4.2.2 环境成本最低 以环境成本最低为目标的微电网运行优化结果如图7所示.可以看出,单从环境成本的角度考虑,由于微型燃气轮机较燃料电池低,燃料电池又较柴油发电机低,在优先考虑环境成本最低的情况下,在微型燃气轮机额定功率范围内,优先考虑微型燃气轮机出力,超出额定功率后再考虑燃料电池、柴油发电机出力,与图7优化结果相符. 图6 运行成本最小目标下微电网优化结果Fig.6 Optimal results of microgrid of minimum operation cost 图7 环境成本最低目标下微电网优化结果Fig.7 Optimal results of microgrid of minimum environmental cost 4.3 多目标优化结果 表3 不同目标下的优化结果 目标函数λ1运行成本/元环境成本/元运行成本最小12210.37162.43环境成本最低02305.61147.97多目标优化0.82236.13158.110.22283.62151.83 采用线性加权的方法给各子目标函数赋予权重,将多目标优化问题转化为单目标优化问题.目标函数为F=λ1F1+λ2F2,其中λ1、λ2分别为子目标权重系数,且满足λ1+λ2=1.对λ1、λ2分别赋值,不同目标下的优化结果如表3所示.以运行成本最小作为单目标得到的环境成本较最低环境成本高9.77%,环境效益较差;以环境成本最低作为单目标得到的运行成本较最小运行成本高4.31%,经济效益较差;多目标优化得到的运行成本分别比最小运行成本高1.17%和3.31%,环境成本分别比最低环境成本高6.85%和2.61%,能够综合协调经济效益和环境效益.多目标优化模型比单目标优化模型在一定程度上能够获得更好的优化结果,可以以较小的运行成本达到尽量好的环境效益,实现了兼顾节能、环保的发电调度.在实际应用中,应结合用户的不同需求,综合考虑外部市场环境的影响. 通过仿真分析比较考虑实际约束的功率差控制策略与恒功率控制策略,得出前者在均衡用电负荷、完成削峰填谷控制目标等方面更能贴近实际应用需求.采用功率差控制策略确定蓄电池的运行方式,并以此作为可控型微电源优化运行的基础.在考虑各约束条件的基础上,以微电网的运行成本、环境成本为优化目标,构建了孤立微电网运行优化模型.采用改进的遗传优化算法从单目标和多目标两个层面进行求解,并分析了微电网中可控型微电源的出力分配,为孤立微电网运行优化的研究提供了参考. [1] HATZIARGYRIOU N, ASANO H, IRAVANI R, et al. Microgrids[J]. IEEE power and energy magazine, 2007, 5(4):78-94. [2] 王成山,杨占刚,王守相,等. 微网实验系统结构特征及控制模式分析[J].电力系统自动化,2010,34(1):99-105. [3] 王成山,于波,肖峻,等. 平滑可再生能源发电系统输出波动的储能系统容量优化方法[J]. 中国电机工程学报, 2012, 32(16):1-8. [4] 尤毅, 刘东, 钟清,等. 主动配电网储能系统的多目标优化配置[J]. 电力系统自动化, 2014,38(18):46-52. [5] TSIKALAKIS A G, HATZIARGYRIOU N D. Centralized control for optimizing microgrids operation[J]. IEEE transactions on energy conversion, 2008, 23(1): 241-248. [6] DIMEAS A L, HATZIARGYRIOU N D. Agent based control for microgrids[C]//Proceedings of IEEE Power Engineering Society General Meeting. Tampa, 2007:1-5. [7] 秦亚斌, 韩肖清, 王康宁. 含混合储能的微网孤网运行能量管理策略[J]. 河南科技大学学报(自然科学版), 2014,35(4):31-37. [8] 丁明,张颖媛,茆美琴,等.包含钠硫电池储能的微网系统经济运行优化[J].中国电机工程学报,2011,31(4):7-14. [9] 陈洁,杨秀,朱兰,等. 不同运行调度模式下微网经济运行对比分析[J]. 电力自动化设备,2013,33(8):106-113. [10] 王锐, 顾伟, 吴志. 含可再生能源的热电联供型微网经济运行优化[J]. 电力系统自动化, 2011, 35(8):22-27. [11] MOHAMED F A,KOIVO H N. System modelling and online optimal management of microgrid using mesh adaptive direct search[J]. Electrical power and energy systems, 2010, 32(5): 398-407. [12] MOHAMED F A,KOIVO H N.Online management of microgrid with battery storage using multiobjective optimization[C]//Proceedings of International Conference on Power Engineering,Energy and Electrical Drives.Setubal,2007:231-236. [13] 丁明,张颖媛,茆美琴,等.集中控制式微网系统的稳态建模与运行优化[J].电力系统自动化,2009,33(24):78-82. [14] 刘小平,丁明,张颖媛,等.微网系统的动态经济调度[J].中国电机工程学报,2011,31(31):77-84. [15] 陈洁,杨秀,朱兰,等.微网多目标经济调度优化[J].中国电机工程学报,2013,33(19):57-66. [16] 牛铭,黄伟,郭佳欢,等. 微网并网时的经济运行研究[J].电网技术,2010,34(11):38-42. [17] 毛晓明,陈深,吴杰康,等. 分时电价机制下含蓄电池微网的优化调度[J].电网技术,2015,39(5):1192-1197. [18] 石庆均,江全元. 包含蓄电池储能的微网实时能量优化调度[J].电力自动化设备,2013,33(5):76-82. [19] 刘天琪,江东林. 基于储能单元运行方式优化的微电网经济运行[J]. 电网技术,2012,36(1):45-50. [20] 陈达威,朱桂萍.微电网负荷优化分配[J].电力系统自动化,2010,34(20):45-49. [21] 江渝,黄敏,毛安,等.孤立微网的多目标能量管理[J].高电压技术,2014,40(11):3519-3527. (责任编辑:孔 薇) Optimal Operation of Isolated Microgrid System with Battery Storage CHU Yanting1, DONG Haiying1, LI Xiaoqing1,2 (1.SchoolofAutomationandElectricalEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China; 2.SchoolofElectricalEngineering,LanzhouInstituteofTechnology,Lanzhou730070,China) For the optimal operation problem of isolated microgrid, a multi-objective operation optimization method of microgrid with battery was proposed. The method consisted of two parts: the management of operation mode of energy storage unit and the optimization of controllable distributed generation. The control strategy of power difference was used to manage the energy storage unit by taking into account the load demand, power generation expect of renewable resources, and charging state of energy storage unit. For the sake of decreasing economic and environmental cost, the power balance, limit value of distributed generation and ramping constraint were taken into account; the output of controllable distributed generation was distributed by using improved genetic algorithm. This method could not only play a role to cut peak and fill valley and to increase the economic value of energy storage unit, but also ensure isolated microgrid run economically and environmentally. A typical daily optimal operation was taken as an example, the method was verified to be feasible and effective. microgrid; isolated operation; battery; operation optimization 2016-09-22 兰州工业学院青年基金资助项目(14K-003). 褚衍廷(1989—),男,山东济宁人,硕士研究生,主要从事微电网运行优化研究,E-mail:chuyanting2008@163.com;通讯作者:董海鹰(1966—),男,甘肃兰州人,教授,主要从事电力系统运行与控制研究,E-mail:donghy66@163.com. 褚衍廷,董海鹰, 李晓青.含蓄电池的孤立微电网系统运行优化研究[J].郑州大学学报(理学版),2016,48(4):109-115. TM73 A 1671-6841(2016)04-0109-07 10.13705/j.issn.1671-6841.20166903 求解算法
4 算例分析
Tab.2 Data of distributed generations



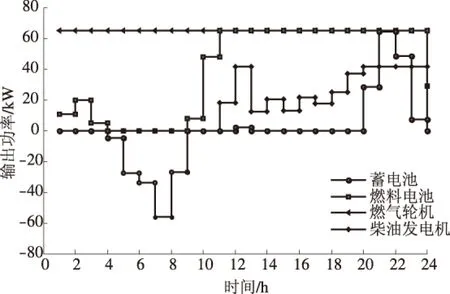
Tab.3 Optimization results of the different objects
5 结论

