粗颗粒物料管道水力输送不淤临界流速计算

邱 灏，曹 斌，夏建新

(中央民族大学生命与环境科学学院，北京 100081)



粗颗粒物料管道水力输送不淤临界流速计算

邱 灏，曹 斌，夏建新

(中央民族大学生命与环境科学学院，北京 100081)

近30年来，固体物料的管道水力输送技术应用越来越广泛。在管道水力输送系统设计中，不淤临界流速是首先需要确定的重要参数，对确保管道安全输送具有重要意义。对于细颗粒物料，已有比较成熟的计算方法，但对粗颗粒物料，不同的计算式差异较大，给参数确定带来困难。在对已有的管道不淤临界流速计算进行比较分析基础上，探讨了颗粒浓度、粒径、密度以及管道直径等因素对不淤临界流速的影响，并分析了计算式结构的差异。整理不同学者针对粗颗粒输送的试验数据，重点分析了不淤临界流速随颗粒粒径加大的变化规律。基于量纲分析法，提出了粗颗粒在管道输送中不淤临界流速计算式，其计算结果与试验数据相对误差在10%以下，基本满足不淤临界流速计算的工程要求。

粗颗粒物料； 管道； 水力输送； 不淤临界流速

固体物料管道水力输送因其效率高、成本低、环境友好等特点成为继公路、铁路和水运之后的第四大运输方式，如昆钢大红山精铁矿输送管线长达171 km，年输送量高达600万t；正在建造的神渭输煤管线输送距离达到750 km[1]。同时，管道充填采矿也被广泛采用[2-3]。对于由细颗粒(粒径d<0.1 mm)组成的浆体，管道输送技术已比较成熟。随着管道水力输送应用范围越来越广，许多工程要求直接输送粗颗粒，如建筑用砂最佳粒径在3～5 mm，如过于细小则会影响混凝土的力学性能指标；深海采矿时管道提升的矿石粒径更粗，甚至可能达到30 mm，其原因是在深海海底进行矿石破碎成本很高，同时，细颗粒难以从尾水中去除，无法满足海洋环境保护的要求。

不淤临界流速，即管道水力运输过程中，固体物料能够连续输送、不淤积的速度。在此流速下，系统运行安全可靠且消耗的能量较少[4]。因此，不淤临界速度是管道输送工程设计首先要确定的重要工艺参数，也是评估管道输送安全的重要依据。目前国内外有关由细颗粒组成的浆体管道输送不淤临界流速的研究成果很多，但对于粗颗粒输送不淤临界流速的研究成果则较少，且计算式和结果之间均存在很大的差异，在管道工程设计时无法提供可靠依据。

本文对现有的管道水力输送不淤临界流速计算式进行比较和分析，利用不同学者的试验数据，得到了适合粗颗粒物料管道水力输送的不淤临界流速计算式。

1 已有不淤临界流速计算式

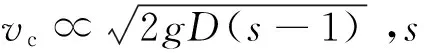
表1 不同学者的管道水力输送不淤临界流速计算式

Tab.1 Formulas for critical velocity given by different scholars

序号作者计算式与主要参数的关系Cvd适用范围1Shook[5]vc=2.43C1/3vC1/4D2gD(s-1)vc∝C1/3vvc∝d1/40.2mm≤d≤5.25mm1.5≤s≤3.9540mm≤D≤580mm2Wasp[6]vc=3.40C0.22v(dD)1/62gD(s-1)vc∝C0.22vvc∝d1/60.25mm≤d≤2.04mm0.01≤Cv≤0.2526.7mm≤D≤139.7mm3Mehmet[7]vc=0.055C0.27v(ρfwdμf)0.3(dD)-0.6gD(s-1)0.07vc∝C0.27vvc∝d-0.30.23mm≤d≤5.34mm0.0075≤Cv≤0.301.04≤s≤2.6825.4mm≤D≤152.4mm4Turian[8]vc=1.82C0.11v(1-Cv)0.25(dD)0.062gD(s-1)vc∝C0.36vvc∝d0.060.02mm≤d≤2.2mm0.028≤Cv≤0.5611.26≤s≤7.4158mm≤D≤101.6mm

图1 已有的不淤临界流速公式计算结果Fig.1 Calculation results of existing different critical velocity formulas

当Rep<1时，CD=24/Rep;

(1)

(2)

当Rep>1 000时，CD与Rep关系不大，通常取CD≈0.44[9]。

(3)

在上述计算式的适用范围内,如选取Cv=0.1，D=100 mm，s=2.65，可以得到图1。从图中可以看出，不同学者的计算结果差异较大，尤其是在粒径较大时，甚至出现了相反的趋势。

2 粗颗粒物料管道水力输送不淤临界流速影响因素

根据颗粒与水流的跟随性，大致可分两种情况。当颗粒粒径较小(细颗粒)时，跟随性好，能与水形成均质浆体；当颗粒粒径较大(粗颗粒)，其速度明显小于水流速度，形成颗粒与水的固液两相流。在颗粒粒径逐渐变大过程中，跟随性逐渐变差，一般情况下可认为，粒径小于0.1 mm颗粒有较好的跟随性，粒径在0.1～1.0 mm之间颗粒跟随性逐渐变差。在管道水力输送过程中，粒径大于1 mm颗粒可认为是粗颗粒。

影响粗颗粒物料管道水力输送不淤临界流速的因素很多,如颗粒浓度、粒径、物料密度和管道直径等因素。

2.1 浓度对不淤临界流速影响

浆体浓度对于不淤临界流速的影响比较复杂，一方面随着颗粒浓度的增加，浆体密度和黏性增加，有效重力减小，使其中的颗粒更难沉降。因此，浓度增加可减小临界流速；另一方面，由于颗粒浓度增加抑制了水流紊动强度，不利于颗粒悬浮，因此必须提高输送速度。在浓度较低时，浓度增加对抑制紊动起主要作用，表现为临界流速随浓度增加而提高，但超过一定浓度后，浓度增加则对减小颗粒沉降速度起主要作用，表现为临界流速随浓度增加而减小[10]。

对于粗颗粒，由于难以与液相形成浆体，当物料浓度较低时(Cv<10%)，固液混合物的黏度主要取决于液相的黏度[11]，因此在输送粗颗粒时，随着物料浓度的增大，不淤临界流速随之增加。当浓度增加到一定值后，由于颗粒存在而使过流面积减小，使实际液相速度大于平均输送流速，临界流速又相应减小。同时，随浓度增加因颗粒沉速快速下降,也使不淤临界流速随之下降[11-12]。

2.2 粒径对不淤临界流速影响

当颗粒粒径较小时(<0.1 mm)，颗粒与流体形成均质浆体，不易沉降，速度较小时便可输送；当颗粒粒径进一步增大后，颗粒有效重力增加，容易沉降，要使颗粒不淤必须加大流速；当颗粒粒径达到一定值后(1～2 mm),大部分以推移状态输送。对于粗颗粒，随着水流速度从小到大变化，其在管道中的运动形态依次出现3种：间歇式推移状态、连续推移状态和悬移状态[13]。

颗粒在水平管道中输送时，水平方向上受到水的拖曳力和管道摩擦阻力作用，垂直方向上受到重力、浮力和流体作用于颗粒的升力作用。在低浓度条件下，管道中粗颗粒运动主要受水流拖曳力控制。拖曳力与颗粒粒径平方成正比，即FD∝d2。在同样的输送速度下，粗颗粒比细颗粒受到的拖曳力作用更强，因此，不淤临界输送速度有可能反而有所减小。

2.3 密度对不淤临界流速的影响

粗颗粒在水中运动时，垂直方向上受重力、浮力以及拖曳力的垂直分量，对于在水中运动的体积确定的颗粒，其浮力一定，重力随密度增加而增加，因此需要拖曳力提供向上的垂直分力相应增加，而拖曳力与流速成正相关，由此，不淤临界流速随粗颗粒密度增加而增大。

2.4 管道直径对不淤临界流速的影响

管道内径对不淤临界流速的影响主要表现在两方面：一方面管道直径越大，其绝对粗糙度越小，水力半径越大，紊动作用越强，使得不淤临界流速减小[14]；另一方面，管径加大，固体颗粒从管底悬浮起来难度更大，更难维持原有的垂线浓度梯度，需要更大的输送速度。从已有的试验资料分析，随着管道内径增加，不淤临界流速也需加大[15]。

3 粗颗粒物料水力输送不淤临界流速计算

图2 部分不淤临界流速试验数据及拟合Fig.2 Testing and simulation results of coarse particle under critical velocity

为进一步深入分析粗颗粒管道输送的不淤临界流速变化规律，将已有的试验数据进行整理和分析，如R.Durand[16]，I.Avci[17]，N.Yotsukura[18]等的研究，见表2。

将上述试验数据中浓度条件相近的进行分组，可以得到3组不同浓度条件下的不淤临界流速变化，如图2。从图2可见，当颗粒较细(d<1 mm)时，临界流速随颗粒粒径增大而增大；当颗粒较粗(d>1 mm)时，不淤临界流速随颗粒粒径增大反而有所减小，但幅度很小。

为得到粗颗粒不淤临界流速的计算公式，采用量纲分析法，并对上表中的数据进行拟合得到(采用的试验数据在1 mm

表2 不同学者不淤临界流速试验数据

Tab.2 Experimental data from past studies

数据来源d/mmD/mCv/%svc/(m·s-1)数据来源d/mmD/mCv/%svc/(m·s-1)Avci[17]0.4210.0520.0502.681.450.4210.0520.1002.681.580.5960.0520.0501.180.490.5960.0520.1001.180.520.5960.0520.1501.180.580.8430.0520.0501.180.520.8430.0520.1001.180.54Grafetal.[19]0.4500.1020.0072.651.550.4500.1020.0102.651.710.4500.1020.0302.651.900.4500.1020.0702.651.980.4500.1520.0082.651.780.4500.1520.0192.652.120.4500.1520.0252.652.270.4500.1520.0542.652.420.8800.1520.0082.651.950.8800.1520.0112.652.040.8800.1520.0302.652.210.8800.1520.0502.652.25Durand[16]0.5850.1080.0502.601.990.5850.1080.1002.602.120.5850.1080.1502.602.441.1500.1080.1002.602.321.1500.1080.1502.602.67Yotsukura[18]0.4400.1500.0502.602.470.4400.1500.1002.602.650.4400.1500.1502.602.712.0400.1500.0252.602.192.0400.1500.0752.602.532.0400.1500.0792.602.412.0400.1500.1002.602.62Sinclair[20]2.2050.0250.1201.740.452.2050.0250.1401.740.47Mehmet[7]1.0900.1500.0152.602.333.2000.0520.0501.410.603.2000.0520.1001.040.273.2000.0520.1001.410.653.2000.0520.1501.410.683.7000.1500.0221.741.623.7000.1500.0361.741.903.7000.1500.0391.741.713.7000.1500.0501.741.883.7000.1500.0551.742.045.3400.1500.0152.551.965.3400.1500.0262.552.035.3400.1500.0272.552.315.3400.1500.0372.552.45

图3 计算值与实测值比较Fig.3 Comparison between calculated and measured values

(4)

将计算值和实测值进行比较，结果见图3，平均误差为8.1%，因此，在D≤150 mm，1 mm≤d≤6 mm，Cv<15%，s>1范围内，可以基本满足工程设计要求。

4 结 语

本文通过理论分析并对其他学者所提出的公式进行对比，结合前人的试验数据拟合分析，得到粗颗粒不淤临界流速预测公式，并将该公式计算结果与实测数据进行比较。结果表明该公式的平均误差在10%以下，满足工程设计参数选择的要求。

[1]陈光国,夏建新.我国矿浆管道输送技术水平与挑战[J].矿冶工程,2015,35(2)：29- 32.(CHEN Guang-guo,XIA Jian-xin.Existing technology and technical challenges in slurry pipeline transportation development in China[J].Mining and Metallurgical Engineering,2015,35(2)：29- 32.(in Chinese))

[2]李公成，王洪江，吴爱祥，等.基于倾斜管实验的膏体自流输送规律[J].中国有色金属学报,2014,24(12)：3162- 3169.(LI Gong-cheng,WANG Hong-jiang,WU Ai-xiang,et al.Gravity transport law of paste based on inclined pipe experiment[J].The Chinese Journal of Nonferrous Metals,2014,24(12)：3162- 3169.(in Chinese))

[3]吴迪,蔡嗣经,杨威,等.基于CFD的充填管道固-液两相流输送模拟及试验[J].中国有色金属学报,2012,22(7)：2133- 2140.(WU Di,CAI Si-jing,YANG Wei,et al.Simulation and experiment of back filling pipeline transportation of solid-liquid two-phase flow based on CFD[J].The Chinese Journal of Nonferrous Metals,2012,22(7)：2133- 2140.(in Chinese))

[4]胡去劣，熊梦婕.尾矿流槽临界流速和临界坡度计算[J].水利水运工程学报,2011(2)：48- 53.(HU Qu-lie,XIONG Meng-jie.Calculation of the critical velocity and the critical slope of trailing hydro-transport in open channels[J].Hydro-Science and Engineering,2011(2)：48- 53.(in Chinese))

[5]SHOOK C A,ROCO M C.Critical deposit velocity in slurry flow[J].AICHE Journal,1985,8：1401- 1404.

[6]WASP E J,KENNY J P,GANDHI R I.Solid-liquid flow-slurry pipeline transportation[M].Rockport：Trans Tech Publ,1977.

[7]MEHMET A K,MUSTAFA G.Critical flow velocity in slurry transporting horizontal pipelines[J].Canadian Metallurgical Quarterly,2001,127(9)：763- 771.

[8]TURIAN R M,HSU F-L,MA T-W.Estimation of the critical velocity in pipeline flow of slurries[J].Powder Technology,1987,51：35- 47.

[9]费祥俊.浆体与粒状物料输送水力学[M].北京：清华大学出版社,1994.(FEI Xiang-jun.Slurry and granular material conveying hydraulics[M].Beijing：Tsinghua University Press,1994.(in Chinese))

[10]汪东，许振良，孟庆华.浆体管道输送临界流速的影响因素及计算分析[J].管道技术与设备,2004(6)：1- 2.(WANG Dong,XU Zhen-liang,MENG Qing-hua.Effect and calculating analysis of critical flow velocity in slurry pipeline[J].Pipeline Technique Equipment,2004(6)：1- 2.(in Chinese))

[11]王绍周,王维春,孙萍,等.粒状物料的浆体管道输送[M].北京：海洋出版社,1998.(WANG Shao-zhou,WANG Wei-chun,SUN Ping,et al.Slurry pipeline transport of granular material[M].Beijing：China Ocean Press,1998.(in Chinese))

[12]费祥俊.浆体管道的不淤流速研究[J].煤炭学报,1997,22(5)：532- 536.(FEI Xiang-jun.Study of non-deposit velocity slurry pipeline[J].Journal of China Coal Society,1997,22(5)：532- 536.(in Chinese))

[13]曹斌,夏建新,黑鹏飞,等.粗颗粒在复杂空间形态管道水力输送中运动形式的研究[J].矿冶工程,2012,32(2)：5- 10,14.(CAO Bin,XIA Jian-xin,HEI Peng-fei,et al.Study on the movement state of coarse-grain during hydraulic transportation in pipeline of complex spatial morphology[J].Mining and Metallurgical Engineering,2012,32(2)：5- 10,14.(in Chinese))

[14]李志铭，何炎平，诸葛玮,等.泥沙管道输送关键流速及其计算方法比较[J].人民黄河,2014,36(9)：16- 19.(LI Zhi-ming,HE Yan-ping,ZHUGE Wei,et al.Comparative analysis the critical velocity and its calculation methods in slurry transportation by pipeline[J].Yellow River,2014,36(9)：16- 19.(in Chinese))

[15]钱宁,万兆惠.泥沙运动力学[M].北京：科学出版社,1991.(QIAN Ning,WAN Zhao-hui.Mechanics of sediment transport[M].Beijing：Science Press,1991.(in Chinese))

[16]DURAND R.The hydraulic transportation of coal and other materialsin pipes[D].London：College of National Coal Board,1952.

[17]AVCI I.Experimentally determination of critical flow velocity in sediment carrying pipeline systems[C]∥Tech Rep Technical University,Istanbul,Turkey,1981.

[18]YOTSUKURA N.Some effects of bentonite suspensions on sand transport in a smooth 4-inch pipe[D].Fort Collins：Colorado State University,1961.

[19]GRAF W H,ROBINSON M P,YUCEL O.Critical velocity for solid-liquid mixtures[D].Bethlehem,Pa：Lehigh University,1970.

[20]SINCLAIR C G.The limit deposit-velocity of heterogeneous suspensions[C]∥Symposium on the Interaction between Fluids and Particles,Third Congress of the European Federation of Chemical Engineers,London,Institute of Chemical Engineering,1962:A68-A762.

Non-silting critical velocity calculation of coarse-grained materials in hydraulic pipeline

QIU Hao，CAO Bin，XIA Jian-xin

(CollegeofLifeandEnvironmentScience，MinzuUniversityofChina，Beijing100081，China)

In the past 30 years,pipeline hydraulic transportation of the solid materials has been applied much more wildly.In the design of the pipeline hydraulic transportation system,the non-silting critical velocity is an important parameter needed to be ascertained at first,which has a great significance for the system operation safety.For the fine-grained materials in the pipeline hydraulic transportation system,many calculation methods can be applied for this parameter.However,for the coarse-grained materials,how to choose the calculation formulas is a difficult problem because of their great different results.In this paper,based on the comparison and analysis of the existing non-silting critical velocity calculation formulas,the influences of the factors including particle concentration,size distribution,density and diameter of the pipeline,on the non-silting critical velocity are discussed especially for the coarse-grained materials,the structure differences of the formulas are compared.A careful analysis of variation law of the non-silting critical velocity changed with the increase of particle size is made by sorting out the experimental data of the coarse-grained materials transport given by different scholars.And based on a dimensional analysis,a new formula to calculate the non-silting critical velocity in a horizontal pipeline hydraulic transportation system has been suggested.The relative errors between the calculated results and the tested data are less than 10%,which can basically meet engineering requirements of calculation of the non-silting critical velocity.

coarse particle; pipeline; hydraulic transportation; non-silting critical velocity

10.16198/j.cnki.1009-640X.2016.06.015

邱灏，曹斌，夏建新.粗颗粒物料管道水力输送不淤临界流速计算[J].水利水运工程学报,2016(6):103-108.(QIU Hao,CAO Bin,XIA Jian-xin.Non-silting critical velocity calculation of coarse-grained materials in hydraulic pipeline[J].Hydro-Science and Engineering,2016(6):103-108.)

2015-11-13

国家自然科学基金资助项目(51179213,51339008,51434002)

邱 灏(1990—)，男，湖南益阳人，硕士研究生，主要从事水沙环境方面的研究。E-mail：qhatnight@163.com

TD522

A

1009-640X(2016)06-0103-06