洛伦兹力问题中运动半径的求解方法
◇ 河北 陈宝友(特级教师)
洛伦兹力问题中运动半径的求解方法
◇ 河北 陈宝友(特级教师)
“磁场”是高中物理的主干内容,历年高考中必定出现,特别是带电粒子在匀强磁场中受到洛伦兹力的作用而使粒子做匀速圆周运动的问题,更是每年高考几乎必考的内容之一.

1 直接观察法
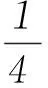
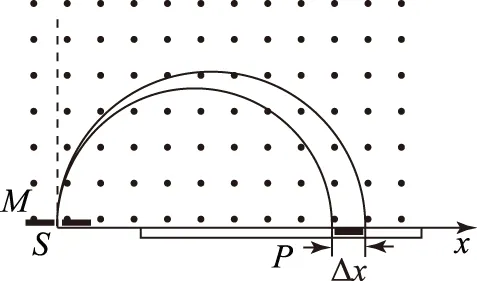
图1
例1磁谱仪是测量α能谱的重要仪器.磁谱仪的工作原理如图1所示,放射源S发出质量为m、电荷量为Q的粒子沿垂直磁场方向进入磁感应强度为B的匀强磁场,被限束光栏M限制在极小的角度内,α粒子经磁场偏转后打到与束光栏平行的感光片P上.(重力影响不计)若能量在E~(E+ΔE)(ΔE>0,且ΔE≪E)范围内的α粒子均垂直于限束光栏的方向进入磁场.试求这些α粒子打在胶片上的范围Δx.


所以能量在E~(E+ΔE)范围内的α粒子打在胶片上的范围为
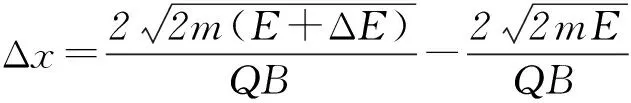
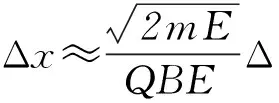
2 三角函数法
由于洛伦兹力的方向跟带电粒子的运动方向垂直,因而很容易在此类问题中构建直角三角形,这就为利用三角函数求运动半径提供了便利条件,所以在已知相关角度的情况下我们可以灵活运用这种方法.
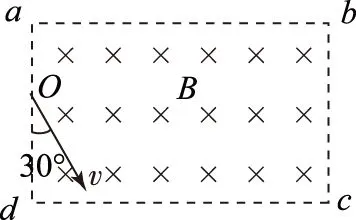
图2
例2如图2所示,一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场.现从矩形区域ad边的中点O处,垂直磁场射入一速度方向与ad边夹角为30°、大小为v0的带电粒子.已知粒子质量为m,电荷量为Q,ad边长为l,重力影响不计.试求粒子能从ab边射出磁场的v0值.

图3
解析这是一道带电粒子在有界磁场中的运动问题,由于磁场边界的限制,粒子从ab射出磁场时速度有一定范围.当v0有最小值v1时,粒子速度方向恰与ab边相切;当v0有最大值v2时,粒子速度方向恰与cd边相切,轨迹示意图见图3.
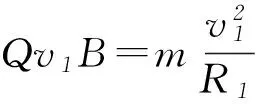
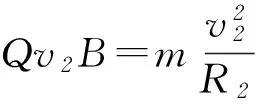
因此,粒子能从ab边射出磁场的v0值为
3 勾股定理法
如上所述,在洛伦兹力问题中非常容易构建直角三角形,且在已知相关角度的情况下可以利用三角函数知识求得运动半径.但在实际问题中,有的并不知道有关夹角而明确了有关长度,这时我们就可以采用勾股定理求解运动半径.

图4
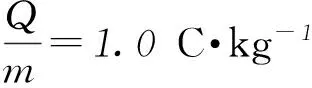
A3m·s-1;B3.75m·s-1;
C4.5m·s-1;D5m·s-1
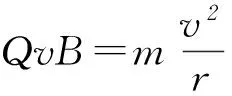
得
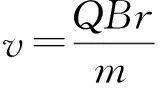
①
(1) 若小球与挡板ON碰撞一次,则轨迹可能如图5-甲.设OO′=d,在△OO′M中,由勾股定理得:
r2=OM2+d2,
②
且
d=3r-ON.
③
联立式②、③得r1=3m, r2=3.75m, 分别代入式①得v1=3m·s-1, v2=3.75m·s-1.
(2) 若小球没有与挡板ON碰撞,则轨迹如图5-乙,设OO′=y,由勾股定理得
,
④
而
y=ON-r3.
⑤

图5
联立式④、⑤得r3=5m,代入式①得v3=5m·s-1,故本题正确答案为A、B、D.
4 正弦定理法
对于直角三角形而言,在已知任意两边的情况下可方便地求出第三边,但在三角形中不出现直角时,自然不能再使用勾股定理.此时如果已知任意两角度及其中一角的对应边,则可利用正弦定理求得另一角的对应边,并进而求得运动半径.

图6
例4在xOy平面内的第一、四象限中,x轴上方有范围足够大的匀强磁场,磁感应强度为B,方向垂直纸面向里,x轴下方有范围足够大的匀强电场,场强为E,方向与y轴正方向相反.在xOy平面内有一点M,M点到O点的距离为L,直线OM与x轴正方向的夹角为θ,如图6所示.现有1个电荷量为Q、质量为m的带负电粒子位于y轴负半轴上的某点,忽略粒子重力.
(1) 将粒子由静止释放,该粒子在第1次由磁场返回电场的过程中恰好通过M点,求该粒子在磁场中的运动半径.

图7
解析(1) 粒子由静止释放,在第一次由磁场返回电场的过程中的运动轨迹容易作出,如图7所示,则由三角函数求得运动半径

(2) 粒子在电场中加速后进入磁场,有

①
此后在匀强磁场中做匀速圆周运动,设速度为v、半径为r,根据牛顿第二定律有
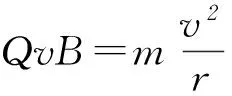
②
设OM与粒子此时圆周运动的半径所对应的夹角为α(如图8),由正弦定理得
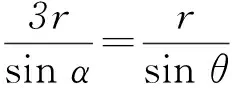
③
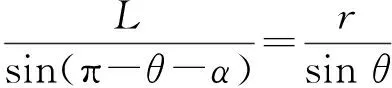
④
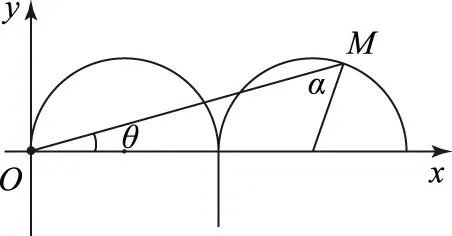
图8
5 余弦定理法
在有的洛伦兹力问题中,若已知的长度比较多,但角度只有一个且不是直角,因此勾股定理与正弦定理均不能使用,但可考虑利用余弦定理来确定半径,进而求解有关物理量.
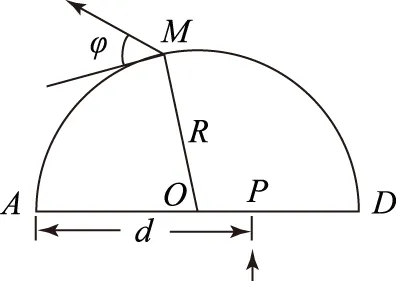
图9
例5如图9所示,在半径为R的半圆形区域中有一匀强磁场,磁场的方向垂直于纸面,磁感应强度为B.一质量为m、带电荷量为Q的粒子以一定的速度沿垂直于半圆直径AD方向经P点(AP=d)射入磁场(不计重力影响).
(1) 如果粒子恰好从A点射出磁场,求入射粒子的速度.
(2) 如果粒子经纸面内M点从磁场射出,出射方向与半圆在M点切线的夹角为φ.求入射粒子的速度.
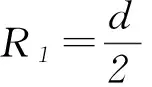
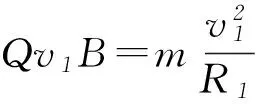
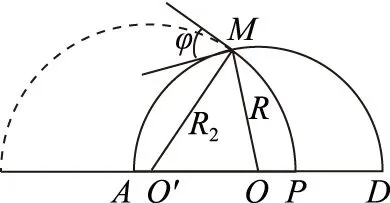
图10
(2) 如图10所示,设O′是粒子在磁场中圆弧轨道的圆心,连接O′M,设O′M=R2.由几何关系得: ∠OMO′=φ,OO′=R2+R-d.
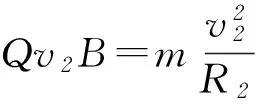
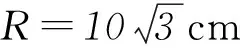
(1) 若电子枪的加速电压U=35V,则电子离开电子枪的速度大小是多少?
(2) 电子以(1)问中的速度进入磁场,且励磁线圈中的电流大小I=1A,求电子在磁场中运动的半径.
(3) 若电子枪的加速电压可以在0到875V的范围内连续调节,且励磁线圈的电流从0.5A到2A的范围内连续调节.求玻璃泡上被电子击中的范围(仅要求在图中玻璃泡壁上用笔标出即可)和电子运动到两边界点对应的半径大小.

图11


图12
(3) 当电压取875 V,电流取0.5 A时,半径最大.最大值r=20 cm,如图12所示.此时电子达到C点,在△OCO′中,由余弦定理有
O′C2=OC2+OO′2+2OC·OO′cos∠COO′
.
解得
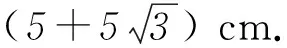
6 相似三角形法
在有的洛伦兹力问题中,若已知的长度比较多,但角度不清楚,此时即可考虑利用相似三角形来确定半径,进而求解有关物理量.
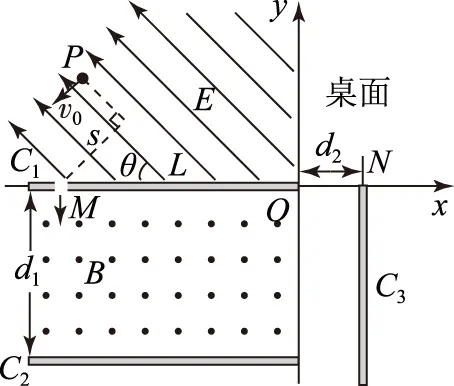
图13
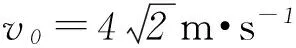
(1) 匀强电场的场强大小;
(2) 要使带电小球无碰撞地穿出磁场并打到平板C3上,求磁感应强度的取值范围.

图14
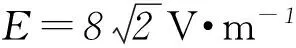
小球刚好不与C2板相碰时磁感应强度最小设为B2,此时粒子的轨迹半径为R2,由几何关系有R2=d1=0.6 m, 解得B2=2/3 T.
综合得磁感应强度B的取值范围是2/3 T~1 T.
由上述各例不难看出,在求解有关洛伦兹力的问题中,关于半径的确定方法尽管五花八门,林林总总,但经常用到的都是三角函数和勾股定理等,我们只要依据题意中提供的有关条件,灵活选择合适的方法即可顺利求得半径,进而求得相关物理量.
河北省衡水市郑口中学)

