一道数学高考题的多解与探究
◇ 北京 李艳茹
一道数学高考题的多解与探究
◇ 北京 李艳茹
1 题目与简析
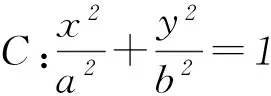
(1)求椭圆C的方程及离心率;
(2)设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
本题属于解析几何问题,主要考查的是椭圆的方程及其简单的几何性质,以及直线和椭圆的位置关系,考查学生分析问题、解决问题的能力,同时也考查了运算能力.
2 解题方法探究
第(1)问可以通过解方程求解,即将点A、B的坐标代入椭圆方程解出a2和b2(或者根据椭圆简单的几何性质直接得出a和b),从而得出椭圆的方程.再依据椭圆中a、b、c的关系求出c,最后由离心率公式得出椭圆的离心率.第(2)问有多种解法,现对不同解法做简单的分析.
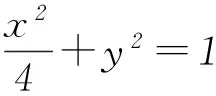
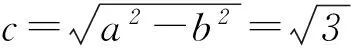
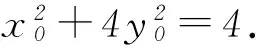
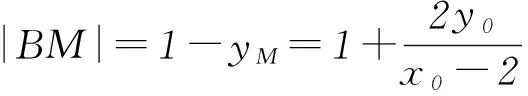
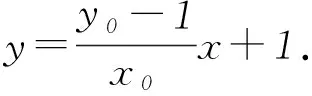
所以四边形ABNM的面积
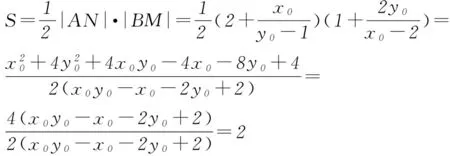
从而四边形ABNM的面积为定值.
点评该解法是将题目的文字叙述翻译成了符号语言,以设椭圆上的点P(x0,y0)坐标为出发点,利用直线PA和PB的方程得出点M、N的坐标,用x0、y0表示出线段|AN|和|BM|的长,再利用四边形ABNM对角线垂直的特征得出四边形ABNM的面积,此种解法计算量较小.
方法2设直线PA方程为y=k(x-2)(k>0), 当x=0时,yM=-2k,即M(0,-2k), 所以|BM|=|1-yM|=1+2k.
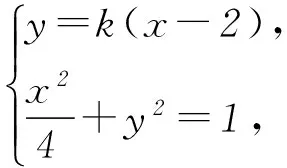
(1+4k2)x2-16k2x+16k2-4=0,
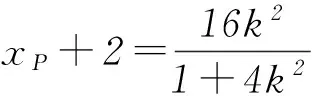
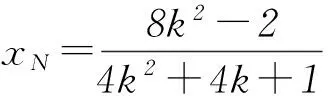
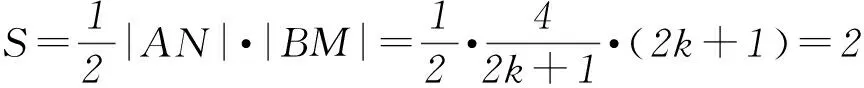
从而四边形ABNM的面积为定值.
点评该解法利用直线与椭圆的位置关系,以设直线PA的方程为出发点,通过解析几何的常用解法,直线方程与椭圆方程联立消元得到关于x的一元二次方程,再利用根与系数关系得出点P的坐标,进而写出直线PB的方程.利用直线PA和PB的方程得出点M、N的坐标,用k表示出线段|AN|和|BM|的长,再利用四边形ABNM对角线垂直的特征得出四边形ABNM的面积,此法只引进了一个变量k,计算量比较大.
方法3设直线PA方程为y=k1(x-2)(k1>0). 当x=0时,yM=-2k1,即M(0,-2k1),所以|BM|=|1-yM|=1+2k1.
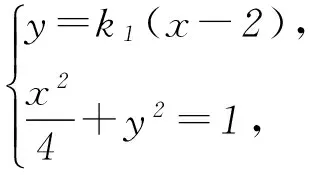
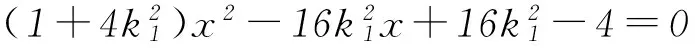
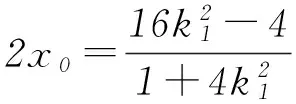
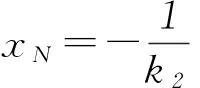
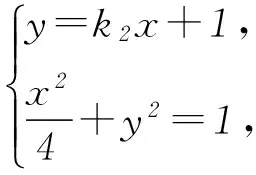
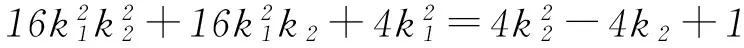
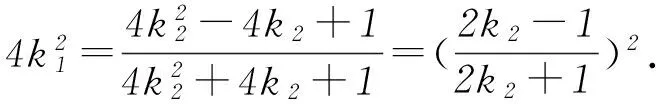
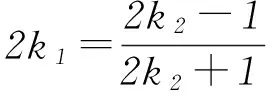
所以四边形ABNM的面积
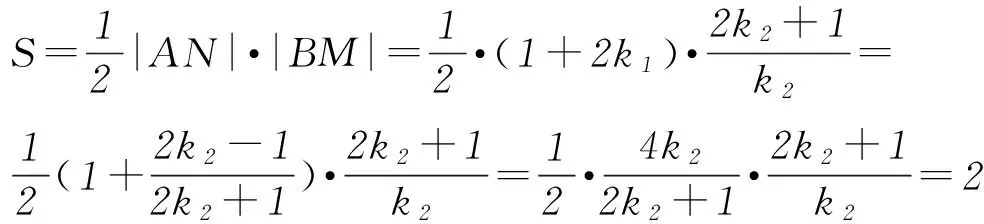
从而四边形ABNM的面积为定值.
点评该解法利用直线与椭圆的位置关系,以设直线PA和直线PB的方程为出发点,通过解析几何的常用解法,直线PA方程与直线PB的方程分别与椭圆方程联立消元得到关于x的一元二次方程,再利用根与系数关系得出点P的2种横坐标的表示形式,进而得出2个斜率k1和k2的关系,再利用直线PA和PB的方程得出点M、N的坐标,用k2和k1分别表示出线段|AN|和|BM|的长,再利用四边形ABNM对角线垂直的特征得出四边形ABNM的面积,此法只引进了2个变量k1和k2,计算量比较大.
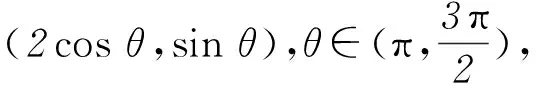
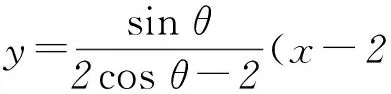
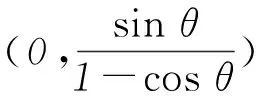
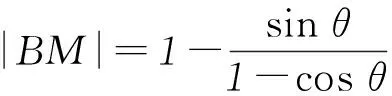
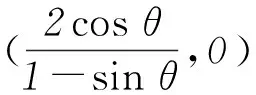
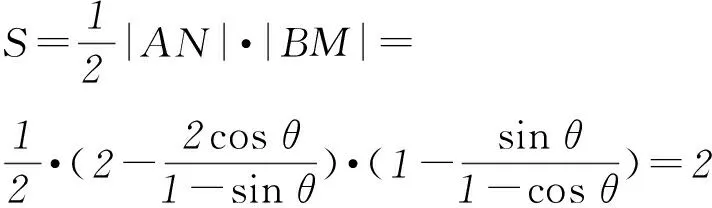
从而四边形ABNM的面积为定值.
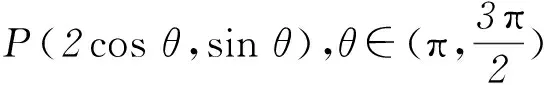
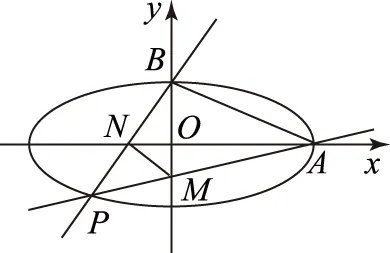
图1

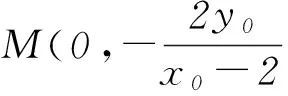
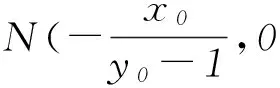
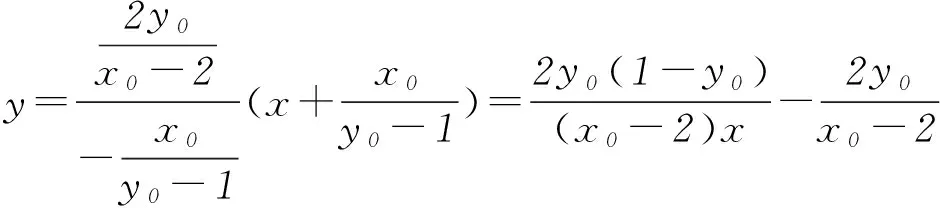
则点P到直线MN的距离
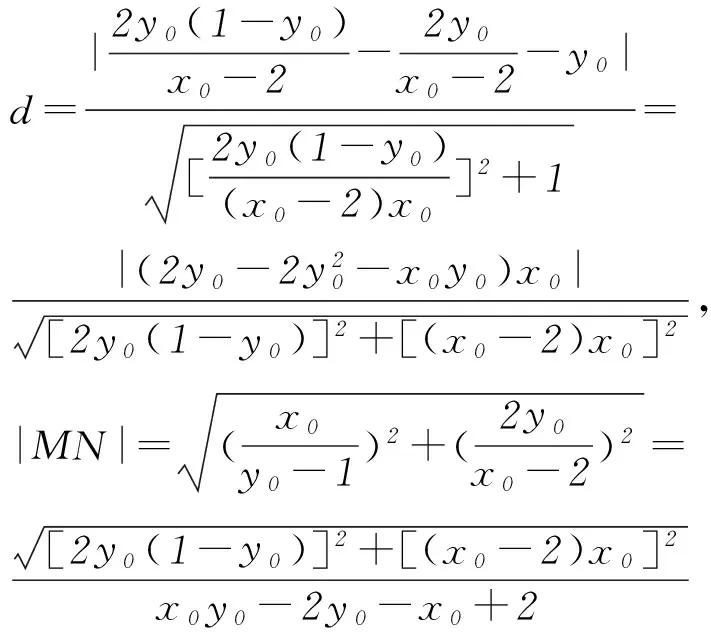
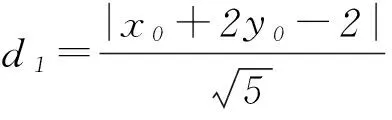
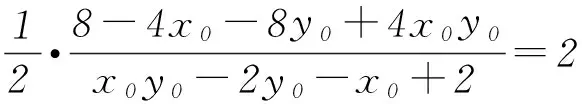
从而四边形ABNM的面积为定值.
点评此解法是利用了间接的方法求四边形的面积,注意到四边形ABNM的面积可以用2个三角形的面积的差来表示.整个解题过程围绕求2个三角形面积展开,即求△PAB的底边|AB|及点P到直线AB的距离d,△PMN的底边|MN|及点P到直线MN的距离d1,此种发方法的计算量非常大,在计算求解的过程中要非常细心才行.
北京市怀柔区第一中学)

