I型糖尿病患者血糖偏微分控制模型(下)
赵家维,曹秀玲,李 璇
(1. 天津大学 理学院,天津 300072;2. 天津财经大学 珠江学院,基础部 天津 301811)
I型糖尿病患者血糖偏微分控制模型(下)
赵家维1,曹秀玲1,李 璇2
(1. 天津大学 理学院,天津 300072;2. 天津财经大学 珠江学院,基础部 天津 301811)
研究了I型糖尿病患者血糖控制系统.在该系统中,针对I型糖尿病患者的生理特点,将热传导偏微分方程应用到血糖控制系统中,从定向控制的角度研究控制输入和控制目标输出的关系.运用Matlab编写程序进行数值模拟,得出控制输出目标(人体正常血糖浓度)所对应的精确控制输入,更好地保证糖尿病患者的身体健康,以免出现低血糖的情况.
I型糖尿病;血糖控制;定向控制;数值模拟
(续接上期)
并且A = QUQ-1,其中
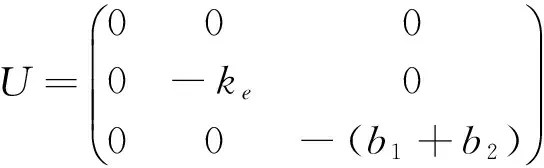
这时A = QUQ-1,并且U是对角矩阵,所以eAt=QeUtQ-1,其中

则

这里令
a(t)=
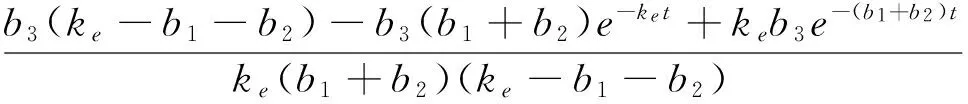

最后,将eAt代入式(11)得
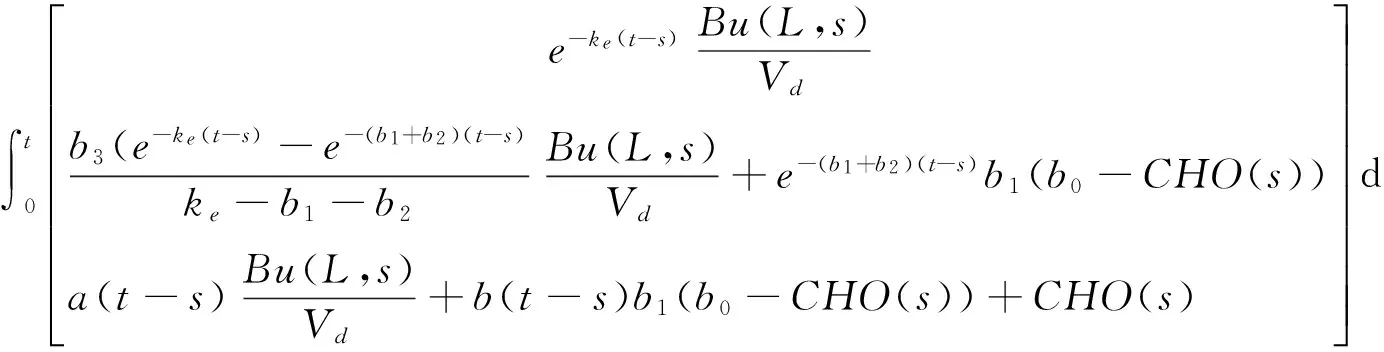
2.3 耦合方程的解
前面,我们得到了u(x, t), i(t),Ge(t),G(t).下面将求解φ(t)与i(t),G(t)的关系.
2.3.1 φ(t)与i(t)的关系
已经得到
u(x,t)=v(x,t)+w(x,t)=
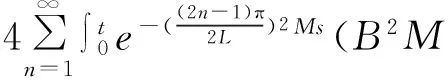


(12)
和
(13)
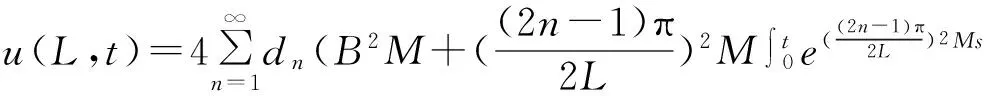
(14)
将式(14)代入式(13),得到
φ(s)ds

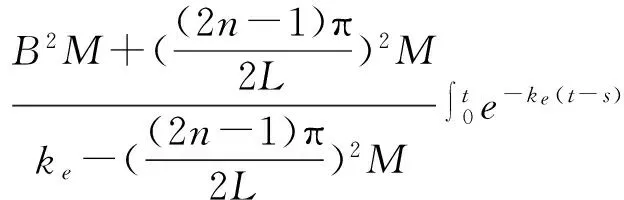
(15)
2.3.2 φ(t)与G(t)的关系
根据3.1和3.2,得到φ(t)与G(t)的关系:

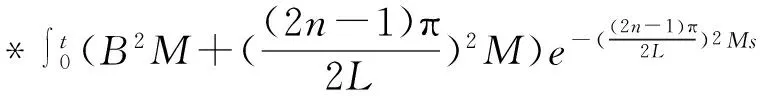
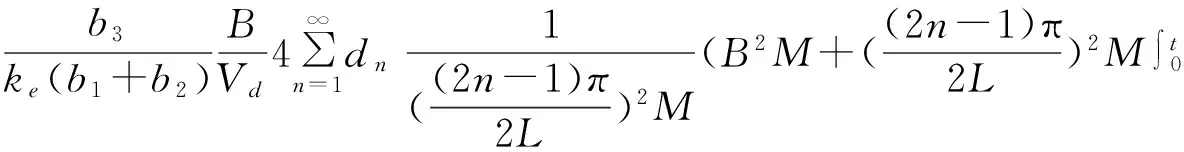
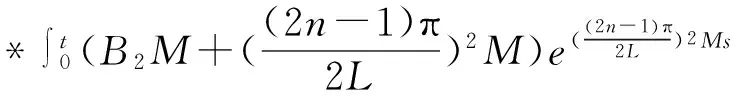

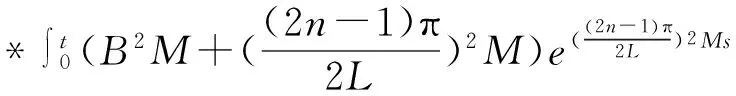
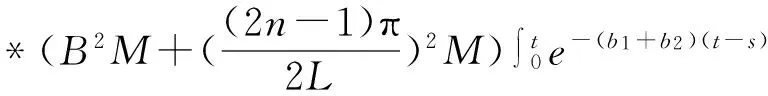

e-(b1+b2)(t-s)φ(s)ds+
(16)
令t→∞,式(16)结果为:
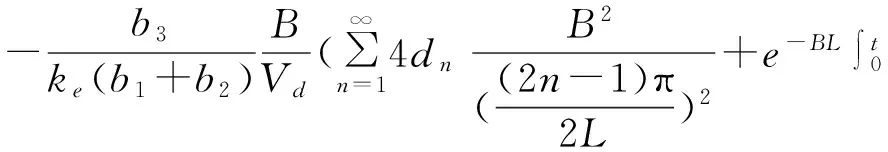
(17)
这样,可以说

(18)
即G(t)依赖于式(16)中的主项.
最后,得出φ(t)与G(t)的关系.
3 血糖-胰岛素的数值模拟
本节对前面描述的模型进行数值模拟.在参数的选择上,沿用已有的研究结果.模型(1)所描述的胰岛素类似物的皮下动力学行为和[3]中的模型类似,所以参数M,B的选择参照[3];而模型(2)是KADIS@模型的一种特殊情况,因此参数选择参照KADIS@ 模型.
各参数的取值如下:
M=9*10-5cm2min-1
B=1.3*10-2min-1ke=0.09min-1
Vd=12*103mLb0=8.0mg/kg
b1=0.018min
b2=0.094minb3=1.73mg·mU-1min-1
由于参数b0与糖尿病患者的体重有关,所以在模拟是我们设定患者的体重为60kg.当空腹血大于等于 126mg/dL时,即可诊断为糖尿病,则假定Ge(0)= G(0)= 1.6mg/mL.其次,此模型是针对IDDM患者建立的,初始时刻体内没有胰岛素,则i(0)= 0.为了方便,我们不考虑患者的饮食,即CHO(t)= 0.
该模型是从定向控制的方向建立的,即输入不同的控制得出不同的结果,见图4、5,左边的曲线代表血液中胰岛素浓度的变化,右边的曲线代表血糖浓度的变化.我们选择了注射10U和20U的胰岛素进行数值模拟.
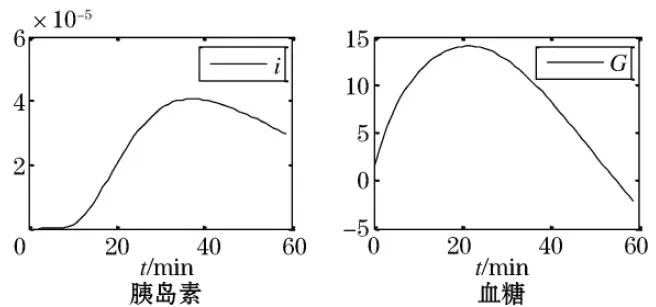
图4 φ(t) = 10 U时的胰岛素和血糖变化

图5 φ(t)= 20 U时的胰岛素和血糖变化
首先,从图4中发现,胰岛素大概在10 min之后大量进入血液,大概在35 min达到最大值,之后逐渐降低,证明了胰岛素在皮下扩散的过程以及胰岛素在体内和葡萄糖相互作用的过程.对于血糖浓度,大概在20 min时才开始下降,是因为模型中没有将患者机体正常运转所消耗的葡萄糖的量考虑在内,即血糖没有消耗,而内源性糖平衡仍然正常地产生葡萄糖,所以出现血糖浓度持续升高的现象;血糖浓度大概在20 min之后逐渐下降,体现了胰岛素和葡萄糖的相互作用,但是大概在50 min后血糖浓度变为了负值,这并不符合实际情况,主要是因为在模型模拟时假设患者没有任何饮食.从分析结果来看大致是符合实际情况的,对于患者机体正常运转所消耗的葡萄糖以及患者的饮食在此模型中是两个难点,目前还没有解决,希望以后有研究者解决.
其次,从两个图的对比来看,如果注射的胰岛素的量较多,同一时间患者体内胰岛素的浓度相对高,而葡萄糖的浓度相对低.这是符合实际情况的,更多的胰岛素能够快速地降低葡萄糖的浓度.
最后,通过数值模拟的结果看出,本文提出的皮下胰岛素动力学模型是合理的,对于更加复杂的情况还待解决.
[1] NUCCI G, COBELLI C. Models of subcutaneous insulin kinetics. A critical review [J]. Computer methods and programs in biomedicine, 2000, 62(3): 249-257.
[2] MOSEKILDE E, JENSEN K S, BINDER C,etal. Modeling absorption kinetics of subcutaneous injected soluble insulin [J]. Journal of pharmacokinetics and biopharmaceutics, 1989, 17(1): 67-87.
[3] TRAJANOSKI Z, WACH P, KOTANKO P,etal. Pharmacokinetic model for the absorption of subcutaneously injected soluble insulin and monomeric insulin analogues [J]. Biomedizinische Technik Biomedical Engineering, 1993, 38(9): 224-231.
[4] BERGMAN R N, COBELLI C. Minimal modeling, partition analysis, and the estimation of insulin sensitivity [J]. Federation Proceedings, 1980, 39(1): 110-115.
[5] STURIS J, POLONSKY K S, MOSEKILDE E,etal. Computer model for mechanisms underlying ultradian oscillations of insulin and glucose [J]. American Journal of Physiology-Endocrinology and Metabolism, 1991, 260(5): E801-E809.
[6] PALUMBO P, PANUNZI S, GAETANO A D. Qualitative behavior of a family of delay-differential models of the glucose-insulin system [J]. Discrete and Continuous Dynamical Systems Series B, 2007, 7(2): 399.
[7] PALUMBO P, PEPE P, PANUNZI S,etal. Glucose control by subcutaneous insulin administration: a DDE modelling approach[C]//Milano: 18th IFAC World Congress, 2011. 1471-1476.
[8] SALZSIEDER E, VOGT L, KOHNERT K D,etal. Model-based decision support in diabetes care [J]. Computer methods and programs in biomedicine, 2011, 102(2): 206-218.
[9] CHEE F, SAVKIN A V, FERNANDO T L,etal. Optimal H∞insulin injection control for blood glucose regulation in diabetic patients [J]. Biomedical Engineering, IEEE Transactions on, 2005, 52(10): 1625-1631.
[10] MARCHETTI G, BAROLO M, JOVANOVIC L,etal. An improved PID switching control strategy for type 1 diabetes [J]. Biomedical Engineering, IEEE Transactions on, 2008, 55(3): 857-865.
[11] PAGUREK B, RIORDON J S, MAHMOUD S. Adaptive control of the human glucose-regulatory system [J]. Medical and biological engineering, 1972, 10(6): 752-761.
[12] RENARD E, COSTALAT G, CHEVASSUS H,etal. Closed loop insulin delivery using implanted insulin pumps and sensors in type 1 diabetic patients [J]. Diabetes Research and Clinical Practice, 2006, 74: S173-S177.
[13] ABU-RMILEH A, GARCIA-GABIN W. A gain-scheduling model predictive controller for blood glucose control in type 1 diabetes [J]. Biomedical Engineering, IEEE Transactions on, 2010, 57(10): 2478-2484.
[14] FABIETTI P G, CANONICO V, ORSINI-FEDERICI M,etal. Clinical validation of a new control-oriented model of insulin and glucose dynamics in subjects with type 1 diabetes [J]. Diabetes technology & therapeutics, 2007, 9(4): 327-338.
[15] ABU-RMILEH A, GARCIA-GABIN W, ZAMBRANO D. A robust sliding mode controller with internal model for closed-loop artificial pancreas [J]. Medical & biological engineering & computing, 2010, 48(12): 1191-1201.
Partial differential glycemic control model for type I diabetes(Ⅱ)
ZHAO Jia-wei1, CAO Xiu-ling1, LI Xuan2
(1. Department of Mathematics, Tianjin University, Tianjin 300072, China; 2. Department of Basic Course,Pearl River College, Tianjin University of Finance and Economics, Tianjin 301811, China)
In this paper, the glycemic control system of type I diabetics was discussed. In this system, the heat equation was applied to the glycemic control system based on the physiological character of type I diabetics, and the relationship between the control input and control objective was researched from the point of view of orientation control. Eventually, some numerical simulations were performed by Matlab program. From the results of numerical simulations, we got the accurate control input corresponding to the control objective guaranteeing the health of diabetics lest the appearance of hypoglycemia.
type I diabetes; glycemic control; orientation control; numerical simulation
2015-09-14.
国家自然科学基金(NSFC-61174080,61104130)
赵家维(1991-),女,硕士,研究方向:控制论.
O174
A
1672-0946(2016)06-0682-04

