扑翼的推力特性与功率特性的实验研究

付鹏, 宋笔锋, 梁少然, 杨文青

(西北工业大学 航空学院, 陕西 西安 710072)

扑翼的推力特性与功率特性的实验研究

付鹏, 宋笔锋, 梁少然, 杨文青

(西北工业大学 航空学院, 陕西 西安 710072)

针对扑翼实验动态特性强、测控变量多的特点，设计了一种实验专用的扑动机构，在实现对扑动频率和扑动幅度精确调控的同时，集成了对瞬时扑动角度和输入功率的测量功能，建立了一套适用于扑翼风洞实验的测控系统，能够实现对动态气动力、扑动角度、扑动翼输入功率等量的实时同步测量；在此基础上针对扑翼的推力特性和功率特性进行了风洞实验研究，着重分析了在不同扑动频率和不同扑动幅度情况下扑翼的推力与功率特性；实验结果表明，在研究的范畴内，扑动频率和扑动幅度的增大都有利于推力的产生，但都会增大对应的功耗；推力和功耗都随St的增大呈“J”型曲线增长，当St小于0.25时，推力和功耗的增长趋势较缓，随着St的增大，尤其当St大于0.3时，推力和功耗将大幅增大。

微型扑翼飞行器；推力特性；功率特性；风洞实验；测控系统

近年来，由于扑动飞行方式在微型飞行器范畴内具有的独特优势，已有多个研究机构将研究方向转向了微型扑翼飞行器。对于微型扑翼飞行器，扑动翼产生的推力和功率消耗直接决定了飞行器的机动能力和续航时间，因而研究扑翼的推力特性和功率特性对提高飞行器的性能起着重要作用。

扑翼独特的非定常运动方式使其研究难度远大于对常规固定翼的研究[1]。在通常的研究方法中，风洞实验由于其直观可靠的特点，一直是扑翼研究中的一种重要手段。在国内的研究中，西北工业大学的邵利民等[2]较早地利用风洞实验研究了扑翼的气动特性，探究了不同外形的扑动翼的气动规律；随后南京航空航天大学的段文博等[3]在开口风洞中研究了主动变形扑动翼的气动特性；以上研究主要侧重于对扑动翼平均气动力和功率的研究，未对扑动翼在扑动过程中的瞬时气动力和瞬时功率进行深入分析。在国外的研究中，弗罗里达大学的Pin Wu等[4]通过高速摄像系统研究在悬停状态下扑翼的柔性变形与推力的关系；而亚利桑那大学的Sergey Shkarayev等[5]在风洞实验中通过定频率和定功率的方法研究了扑动翼平均推力的变化特性。

在以往的扑翼实验研究中，受限于当时的实验手段，往往更注重对扑动翼的平均气动力进行研究，而忽略扑翼在扑动过程中的瞬态气动特性；此外，即便有些研究中涉及到了扑动翼的功率特性，但其测量的功率中包含了驱动机构消耗的功率，并未直接得到扑动翼的输入功率。扑翼飞行器是一种动态的飞行方式，扑动翼产生的推力和功率消耗都呈现强烈的非定常特性，只有分析扑动过程中的瞬时特性才能逐渐认识扑翼飞行的本质，而仅对平均特性的研究则无法达到这种效果。基于此，论文设计了一套能够直接测量扑动翼的瞬时气动特性和瞬时功率特性的实验系统，并在该系统的基础上实现了对扑翼推力特性和功率特性的研究。

1 实验系统设计

传统的实验装置并不能满足本次实验的要求，论文针对本次实验对扑动机构进行了重新设计，并利用新的测控终端和驱动软件建立了全新的实验测控系统，使其在功能和精度上都有较大提升。

1.1 实验风洞

实验风洞为西北工业大学的低湍流度风洞(如图1所示)，该风洞为直流吸式闭口风洞，风洞的特殊设计能够将试验段的湍流度降至接近大气中湍流度的水平。其具体参数如表1所示：

图1 西北工业大学低湍流度风洞

项目参数风洞全长/m39.5试验段尺寸/m2.8×1.2×1.05试验段风速范围/(m·s-1)3～22湍流度/%≤0.02迎角变化范围/(°)-10～36

1.2 测力天平

为满足扑翼测力的要求，实验选择了美国ATI公司的Nano SI-12-0.12多轴力/力矩传感器作为扑翼实验的测力天平。该天平能够兼顾量程合适、体积小、灵敏度高、响应速度快等优点，非常适合微型扑翼飞行器的风洞实验。天平参数如表2所示。

表2 天平性能参数

1.3 扑动机构

扑动机构是扑翼实验的关键部件之一，论文为此次实验研制了专用的扑动机构，该机构除了具有驱动扑动翼运动的功能外，同时还集成了多个测控装置。如图2所示，扑动机构基于四连杆原理进行设计，驱动电机通过输出盘和连杆的传动，将电机的旋转运动转换为左右2个摇臂的往复扑动，该扑动机构具有以下特点：

1) 驱动电机采用Faulhaber伺服电机，具有控制响应快和控制精度高的特点，实验中对扑动频率的控制精度能够达到0.01 Hz；

2) 机构采用输出盘代替常规四连杆机构中的曲柄，输出盘上分布有多个螺纹调节孔，每个调节孔距输出盘中心的距离各不相同，当连杆与不同的调节孔相连时，摇臂具有不同的扑动幅度，实验中能够分别实现35.2°、47.7°、54.2°、61.0°、68.3°和76.1° 6种扑动幅度；3) 左右2个摇臂之间通过齿轮啮合，能够保证左右摇臂的完全对称扑动，且摇臂上下表面分别粘贴了2片半导体电阻应变片，4片应变片以惠斯通电桥的形式连接构成力矩传感器，能够测量摇臂的输出力矩；4) 在左摇臂的转动轴上集成了基于霍尔效应的非接触式角度传感器，该传感器的动态响应时间小于0.6 ms，角度分辨率小于0.09°，能够较准确地测量摇臂的瞬时扑动位置，并能够通过差分运算获得摇臂的瞬时扑动角速度和角加速度。

图2 扑动机构的结构图

1.4 测控设备

整个系统通过NI公司的CompactDAQ-9188测控终端完成硬件集成，如图3所示。

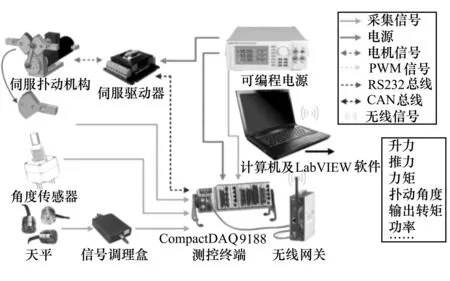
图3 测控系统的集成

系统以基于虚拟仪器的LabVIEW软件进行硬件驱动，在实现软硬件无缝连接的同时，能够获得良好的人机交互。通过硬件和软件的集成，系统能够实时测量实验中的升力、推力、力矩、扑动角度、摇臂输出转矩、功率等量。

1.5 实验模型

实验选择课题组研制的扑翼飞行器所用的扑动翼作为实验模型，如图4所示。该扑动模型由碳纤维刚性骨架和柔性聚酯薄膜构成。模型的翼展为600 mm，弦长为100 mm，且在弦向有6%的弯度。

图4 风洞实验模型

2 数据处理方法

2.1 滤波处理方法

在动态实验中，由于结构的振动及电磁干扰的影响，测量数据中会掺杂多种高频杂波[8]。为去除这些高频杂波的影响，实验采用3阶Butterworth低通数字滤波器对采集数据进行滤波处理，考虑到实验中的扑动频率小于10 Hz，因而选择20 Hz作为滤波器的截止频率，图5为扑动频率为6 Hz时滤波前后的升力波形曲线。

图5 滤波前后的升力波形曲线

由图可知，这种滤波方式能够有效去除杂波干扰，但会产生一定的相位移动；如果同时对所有测量量进行相同的滤波处理，各量由于产生了相同的相位偏移量，因而不会改变他们之间的相位关系。

2.2 惯性力的去除方法

实验中测得的力包含真实气动力和扑动翼运动时产生的惯性力，实验在已知扑动翼质量分布和运动状态的条件下采用数值算法分别计算扑动翼在每个时刻的惯性力并去除。扑动翼的惯性力Fine可以由公式(1)计算得到

(1)

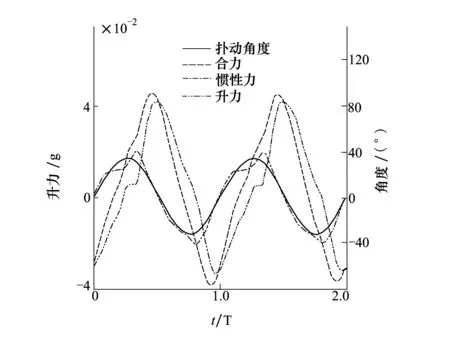
图6 惯性力去除前后的升力曲线

2.3 扑动翼输入功率的计算方法

扑动翼的输入功率P即摇臂的输出功率,该功率可以由公式(2)计算得到

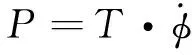
(2)

3 实验结果

由于无法将扑动翼的真实推力和阻力分离,实验测得的推力为真实推力和阻力的合力。为避免驱动电机和扑动机构对扑动翼输入功率的影响,实验通过公式(2)直接得出扑动翼的输入功率。

3.1 扑动频率的影响

1) 扑动频率对瞬时推力和瞬时功率的影响

扑动频率表征扑动翼运动的快慢程度。图7为扑动幅度为35.2°,风速为8 m/s,扑动频率分别为4 Hz、6 Hz和8 Hz时的推力在2个扑动周期内的瞬时变化曲线。由图可知,推力在一个扑动周期内会出现2个波峰和2个波谷。由于扑动翼在0°扑动角度附近的扑动速度最快,此时推力达到峰值;而2个峰值的不同则是由于扑动翼的弯度使其在上扑和下扑过程中的刚度不同所引起的;当扑动翼分别运动到最高点和最低点时,扑动翼的扑动速度接近为0,因而在这2个位置,推力的瞬时值最小。扑动频率的增大意味着扑动翼的运动速度的增大,此时扑动翼的推力也会随之增大,由图7可知,扑动频率增大时,扑动翼瞬时推力的波动幅度也会增大;当扑动频率为8 Hz时,其推力的变化幅度几乎为扑动频率为4 Hz时推力波动幅度的3倍左右。

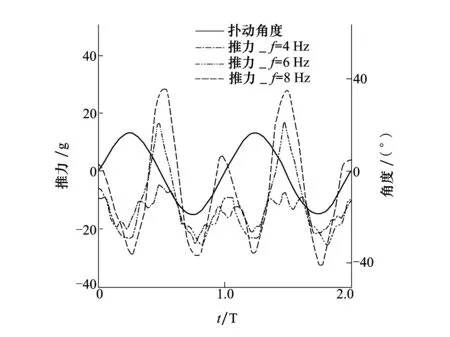
图7 不同扑动频率下的瞬时推力曲线

图8为扑动幅度为35.2°,风速为8 m/s,扑动频率分别为4 Hz、6 Hz和8 Hz时扑动翼的输入功率在2个扑动周期内的瞬时变化曲线。

图8 不同扑动频率下的瞬时功率曲线

由图8可知功率在一个扑动周期内的瞬时变化曲线也出现了2个波峰和2个波谷。两个波峰分别出现在扑动翼上扑和下扑时的0°扑动角度位置附近,因为此时扑动翼上的气动载荷最大,瞬时功率消耗最大;2个波谷则分别出现在扑动翼运动的最高点和最低点,在这2个位置扑动翼的扑动速度最小,气动载荷也最小,所以瞬时功率消耗最小。和图7相比,瞬时功率的变化曲线和瞬时推力的变化曲线的变化规律类似,但出现了少量的相位偏差,这是由扑动翼在扑动过程中的惯性力消耗的功率所引起的。

2) 扑动频率对平均推力和平均功率的影响

图9为扑动幅度为35.2°风速为8 m/s时平均推力和平均功率随扑动频率的变化曲线。图9的曲线表明,当扑动频率增/大时,扑动翼在一个扑动周期内的平均推力和平均功率消耗也会随之增大,当扑动频率由4 Hz增大到8 Hz时,推力增大了近8 g;而平均功率也由0.37 W增大到1.78 W,增大了近4倍。

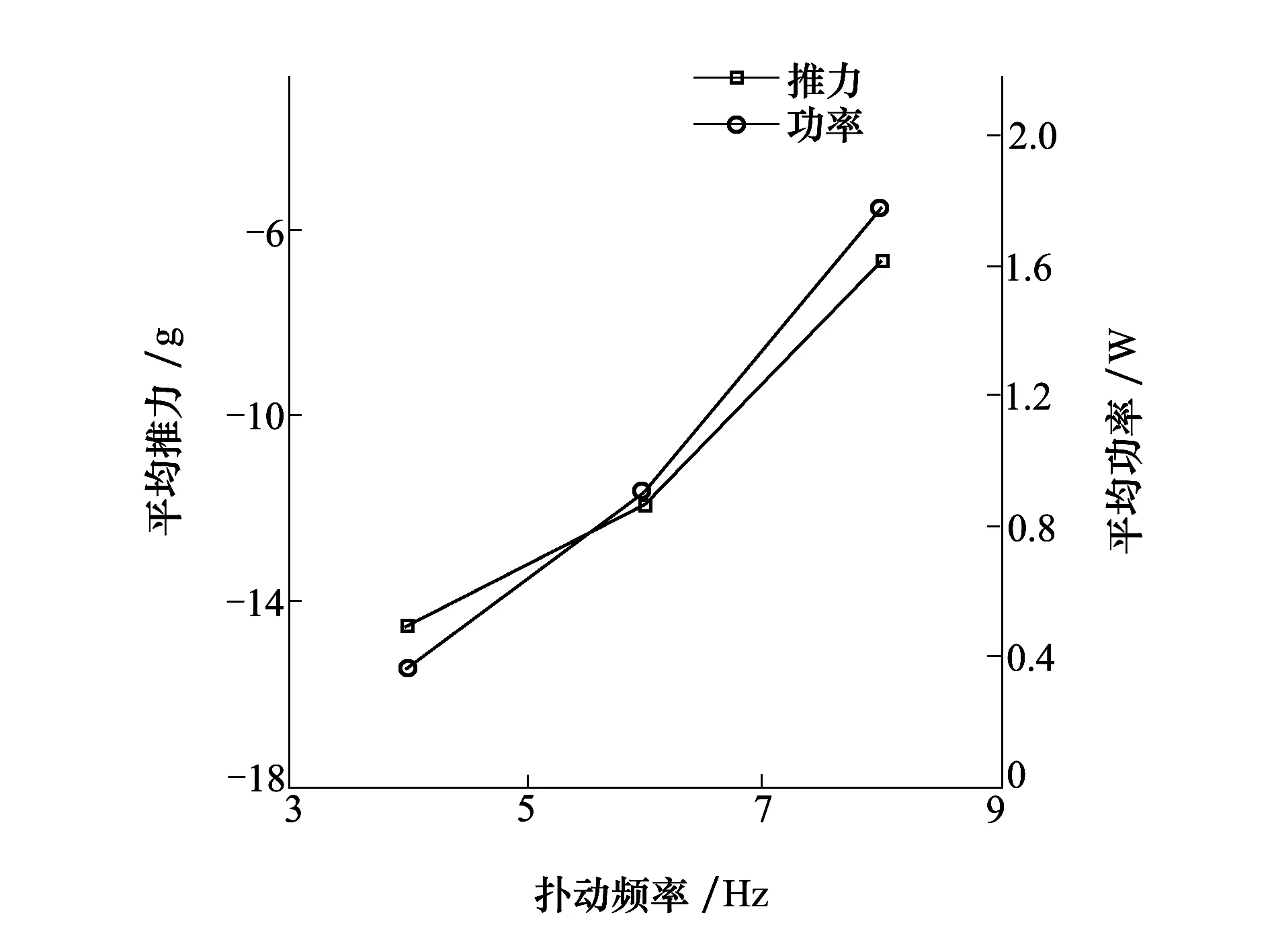
图9 平均推力和功率随扑动频率的变化曲线

3.2 扑动幅度的影响

1) 扑动幅度对瞬时推力和瞬时功率的影响

图10和图11分别为扑动翼在扑动频率为8 Hz,风速为8 m/s,扑动幅度分别为35.2°、47.7°、54.2°和61.0°时2个扑动周期内的瞬时推力和瞬时功率曲线。扑动幅度的增大显著增大了推力曲线的波动幅度;同时功率曲线的波动幅度也会随着扑动幅度的增大而增大;这种变化特性与扑动频率的影响比较类似。

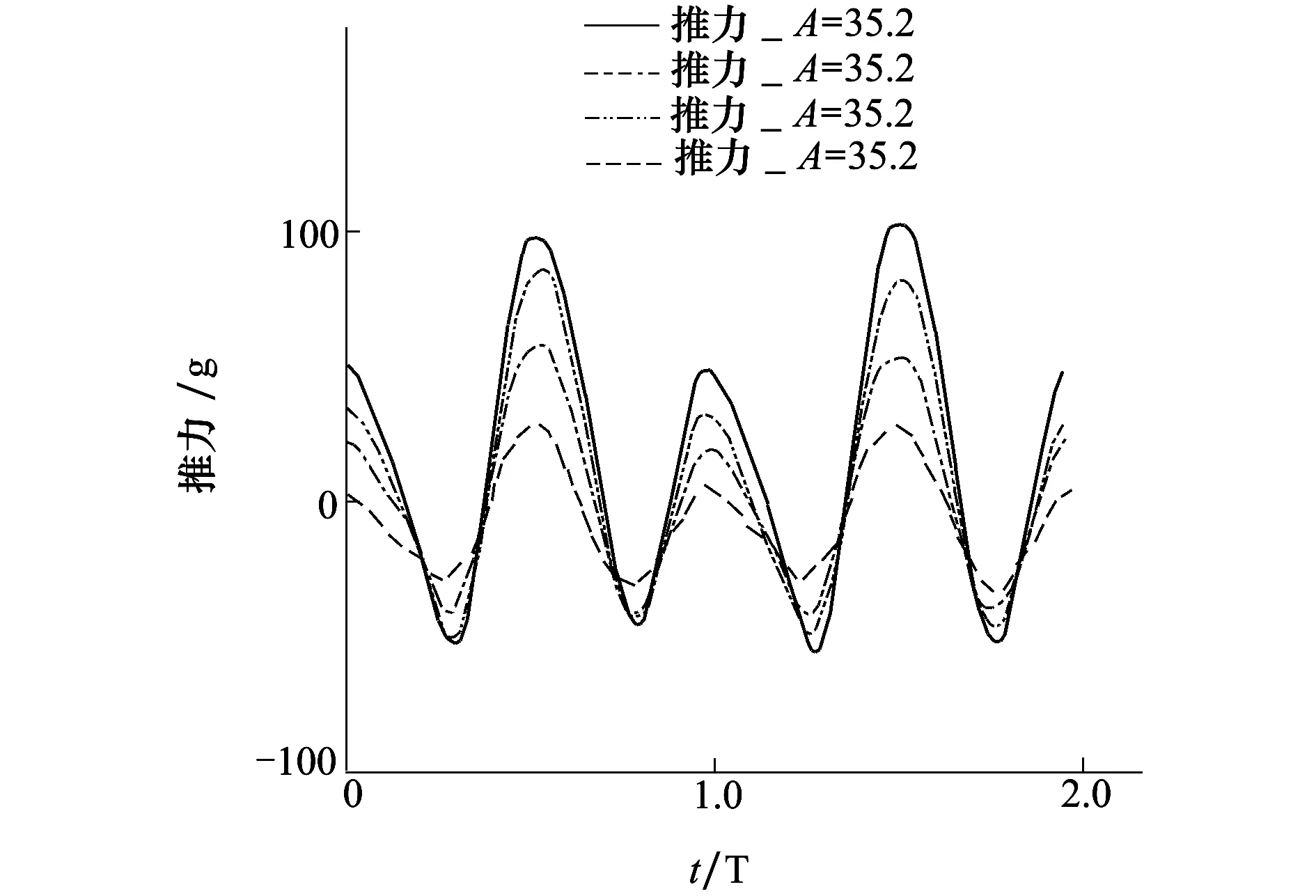
图10 不同扑动幅度下的瞬时推力曲线

图11 不同扑动幅度下的瞬时功率曲线

2) 扑动幅度对平均推力和平均功率的影响

图12为扑动翼在扑动频率为8 Hz,风速为8 m/s时扑动幅度对平均推力和平均功率的影响。

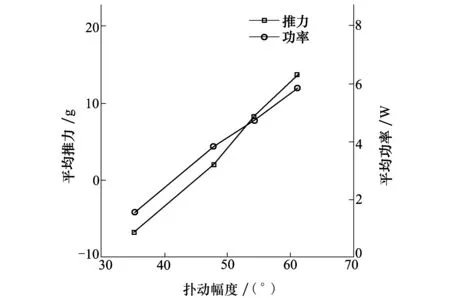
图12 平均功率随扑动幅度的变化曲线

和瞬时的幅值变化类似,当扑动幅度增大时,平均推力和平均功率也随之增大,且和扑动幅度近似呈线性变化的关系。扑动幅度为61.0°时的推力较扑动幅度为35.2°时的推力增大了20 g左右,而平均功率则由增大了约4倍。由此可见增大扑动幅度在增大推力的同时,也增加了功率的消耗。

3.3 斯特劳哈尔数(St)的影响

扑翼的斯特劳哈尔数可以表示为

(3)

式中,f为扑动频率,A=bsin(φ/2),b为扑动翼的展长,φ为扑动幅度,v为来流速度[6]。由于实验中的风速并非扑翼在巡航飞行状态下的实际空速,因此论文以相同风速下的实验数据来说明St的影响。

图13为扑动翼在风速为6 m/s时的平均推力和平均功率消耗随St的变化。总体上扑动翼的平均推力和平均功率消耗都随着St的增大呈“J”型曲线增长;当St小于0.25时,平均推力和平均功率的增长趋势较缓,随着St的增大,尤其是当St大于0.3时,平均推力和平均功率将大幅增大。

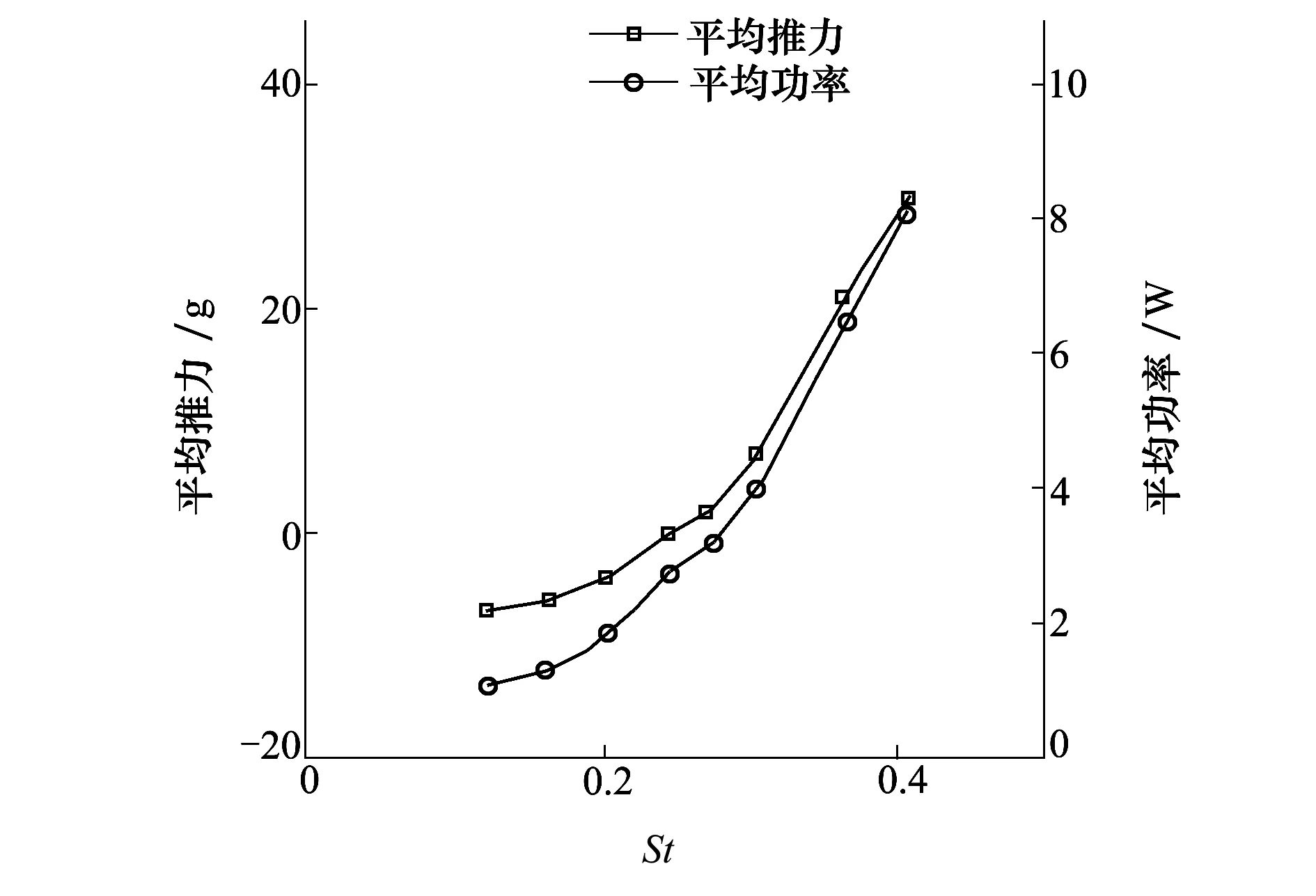
图13 平均推力随St的变化

4 结 论

在传统的扑翼实验系统的基础上,对扑动机构进行了重新设计,不但能够实现对扑动幅度和扑动频率的精确控制,同时还集成了多种传感器,实现了对扑动角度以及扑动翼输入功率等量的实时测量。通过cDAQ-9188测控终端和LabVIEW驱动软件完成对整个系统的整合,建立了一套功能完备的扑翼风洞实验测控系统。利用该系统,研究了扑动翼在不同扑动幅度和不同扑动频率的推力特性和功率特性,实验结果表明:

1) 增大扑动翼的扑动频率能够显著增大扑动翼产生的推力,但会造成扑动翼的输入功率的增大;

2) 扑动幅度的增大有利于推力的产生,且推力随扑动幅度的增大呈线性增长,但较大的扑动幅度也会带来较大的功率消耗,且功率消耗也随扑动幅度的增大近似线性增长;

3) 斯特劳哈尔数是扑动频率和扑动幅度的综合体现,扑动翼的推力和功率消耗都会随St的增大而呈“J”型曲线增长,当St小于0.25时,推力和功耗的增长趋势较缓,随着St的增大,尤其是当St大于0.3时,推力和功耗将大幅增大。

[1] Darryll J Pines, Felipe Bohorquez. Challenges Facing Future Micro-Air-Vehicle Development[J]. Journal of Aircraft, 2006, 43(2): 290-305

[2] 邵立民，宋笔锋，熊超，杨淑利. 微型扑翼飞行器风洞试验初步研究[J]. 航空学报，2007, 28(2): 275-280 Shao Limin, Song Bifeng, Xiong Chao, Yang Shuli. Experimental Investigation of Flapping-Wing MAV in Wind Tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 275-280 (in Chinese)

[3] 段文博，昂海松，肖天航. 主动变形扑翼飞行器的设计和风洞测力试验研究[J]. 航空学报，2013, 34(3): 474-486 Duan Wenbo, Ang Haisong, Xiao Tianhang. Design and Wind Tunnel Test of an Active Morphing Wing Ornithopter[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(3): 474-486 (in Chinese)

[4] Pin Wu, Peter Ifju, Bret Stanford. Flapping Wing Structural Deformation and Thrust Correlation Study with Flexible Membrane Wings[J]. AIAA Journal, 2010, 48(9): 2111-2122

[5] Sergey Shkarayev, Dmytro Silin. Applications of Actuator Disk Theory to Membrane Flapping Wings[J]. AIAA Journal, 2010, 48(10): 2227-2234

[6] Graham K Taylor, Robert L Nudds, Adrian L R. Thomas. Flying and Swimming Animals Cruise at a Strouhal Number Tuned for High Power Efficiency[J]. Nature, 2003,425: 707-710

An Experimental Research about the Characteristics of Thrust and Power of FMAV

Fu Peng, Song Bifeng, Liang Shaoran, Yang Wenqing

(School of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Aiming at the characteristics of flapping-wing MAV (FMAV) wind tunnel experiment which has more variables to be controlled and measured in a dynamic testing environment, a flapping machine is designed for the experiment especially. Beyond the accurate control of flapping amplitude and flapping frequency, the flapping machine also integrates the measurements of instantaneous flapping angle and input power. With the flapping machine, a set of control and measure system to FMAV wind tunnel experiment was built, which realizes the measurement functions of aerodynamic forces flapping angle and input power etc. Based on the system, an experiment about the research of thrust and power characteristics of FMAV is carried on, in which the thrust and power characteristics at different flapping frequencies and different flapping amplitudes are mainly focused on. Within the scope of this study, the experiment result shows increasing flapping frequency and flapping amplitude has a good advantage to thrust generating, but that comes at the price of a higher power consumption; as St increasing, the thrust and power grow as a J-shaped curve, which means the higher the St is, the faster the thrust and power increase.

flapping-wing MAV; thrust characteristic; power characteristic; wind tunnel experiment; measure & control system

V211.7

A

1000-2758(2016)06-0976-06