航空制导炸弹轨迹快速优化研究
聂聪, 张科, 张明环, 王佩
(1.西北工业大学 航天学院, 陕西 西安 710072; 2.航天飞行动力学国家级重点实验室, 陕西 西安 710072)
航空制导炸弹轨迹快速优化研究
聂聪1,2, 张科1,2, 张明环1,2, 王佩1,2
(1.西北工业大学 航天学院, 陕西 西安 710072; 2.航天飞行动力学国家级重点实验室, 陕西 西安 710072)
针对制导炸弹对地攻击的垂直打击的弹道特点,研究了多约束条件下的轨迹优化问题,提出了一种基于hp自适应Radau伪谱法(hp-RPM)的迭代求解策略。该方法允许不同区间的插值多项式的阶次不同,并以轨迹曲率作为重新分配配点以提高区间求解精度的依据,当各配点处的计算精度达到设定的误差允许范围时,迭代停止。以某航空制导炸弹为对象进行轨迹快速优化,仿真结果表明,该方法能够在多约束条件下快速生成满足要求的轨迹,且解的Hamilton函数满足最优性条件,与常规方法相比,平均增程效果达到11.45%。
制导炸弹;轨迹优化;残差;hp自适应;Radau伪谱法
航空制导炸弹具有有效载荷比高、命中精度高、成本相对低廉等优点,是作战飞机近距空中支援、执行纵深打击、压制和摧毁敌方防控系统等任务最有效的内埋式武器[1]。由于无发动机提供动力,其射程主要取决于投放时的高度、速度,因此需要进行轨迹优化,一般采用“滑翔+俯冲攻击”的方案,但这种做法并不能得到最优的轨迹。
从原理上讲,轨迹优化问题可归结为多约束下的非线性最优控制问题,有间接法和直接法[2]2大类求解方法。间接法能够求得精确解,但存在初值难以估计,收敛性无法保证的问题[3]。而直接法是将最优控制问题转化为有限维的非线性规划问题(NLP),应用NLP求解器进行求解。直接法中的配点法,尤其是近期发展起来的伪谱法,因其计算效率上的优势,逐渐成为求解NLP问题的研究热点。
Elnagar等[4]首次对伪谱法的转换原理,收敛速度、求解效率等方面做了深入研究,奠定了伪谱法求解最优控制问题的基础。伪谱法是将时间离散化为若干离散点,指标函数、微分方程和约束条件由离散点上的状态变量、控制变量表示,再利用NLP求解器求解,相比于传统的智能优化算法在计算时间、控制律的平滑度等方面具有明显的优越性[5]。常见的伪谱法包括:Legendre伪谱法(LPM)、Gauss伪谱法(GPM)、Radau伪谱法(RPM)。Huntington等[6]指出上述3种方法在计算精度方面,GPM、RPM相当,均高于LPM;Gandhi等[7]研究表明在给定求解精度的条件下,RPM比GPM的计算代价更小;Rexius等[8]基于RPM研究了在气动加热、禁飞区等多种约束条件下的高超声速飞行器的轨迹优化问题;袁宴波等[9]研究了Radau伪谱法在最优滑翔弹道应用方面的问题,给出了基于协态映射原理的数值解验证方法。上述方法由于其节点分布形状固定,容易导致需要较高维的插值多项式才能得到理想的近似解,甚至在采用高维多项式后仍然得不到理想的近似解。而自适应hp伪谱法具有计算稀疏性、快速收敛性的特点,对于需要改进求解精度的区间,可细化网格或提高多项式的阶次,这种方法能够大大减小计算代价,在多约束下的轨迹快速优化问题中,具有较大的优势。本文利用基于hp自适应Radau伪谱法(hp-RPM)的优点,采用hp-RPM求解策略对航空制导炸弹在多约束条件下的滑翔轨迹进行快速优化。
1 轨迹优化问题
1.1 航空制导炸弹纵向运动模型
轨迹优化任务中,一般只考虑纵向运动的情况,为加快算法的收敛速度,宜采用无量纲化的制导炸弹纵向运动模型。
引入参考量Lr、Vr,则无量纲纵向运动模型为:
(1)
升力系数CL、阻力系数CD可近似为攻角的函数:
(2)
式中,Ma为飞行马赫数;CL1、CD0、CD2为在不同马赫数下根据攻角α拟合得到的气动力系数。气动参数根据某航空制导炸弹的启动数据拟合获得,拟合结果如图1所示。

图1 某航空制导炸弹升阻曲线
大气密度、音速采用标准大气拟合模型,其精确度能够满足航空制导炸弹的飞行空间。
(3)
1.2 约束条件
根据制导炸弹攻击目标的特点,对边界条件有一定的约束,如大的弹着角、末端速度,这样能够保证制导炸弹具有一定的侵彻能力。
1) 边值约束
初值约束:
(4)
终端约束:
航空制导炸弹对地攻击对弹道倾角和碰撞速度有一定的要求,以保持一定的动能侵彻目标,即
y(tf)=yfV(tf)=yfθ(tf)=θf
(5)
2) 过程约束
航空制导炸弹因无推力,操纵舵效率有限等因素,其需要满足一些诸如过载、攻角变化率、攻角幅值等的限制,建立如下过程约束条件:
(6)

1.3 目标函数
对于轨迹优化,在满足约束条件的前提下,射程越远意味着攻击范围更广,因此,取目标函数为
minJ=-x(tf)
(7)
2 hp-RPM求解最优轨迹
2.1 Radau基本原理
Radau伪谱法将控制变量和状态变量离散化为时间轴上子区间[tk-1,tk]的一系列Legendre-Gauss-Radau(LGR)点,通过构造Lagrange插值多项式对其进行逼近,并对该多项式的求导以代替动力学微分方程[10]。
1) 时域变换
Radau伪谱法的定义域为[-1,1],而实际问题的定义域为[t0,tf],将[t0,tf]分成K个网格,且∀t∈[tk-1,tk],k=1,…,K,t0=t1<… (8) 2) 状态变量与控制变量的插值近似 (9) (10) 3) 动力学微分方程约束转换为代数约束 对(9)式求导,有 (11) 则Nk个LGR点上的动力学微分方程约束变为代数方程约束,即 (12) 4) 约束条件的离散化 子区间内Nk个配点上的路径不等式约束为 (13) 边界条件 (14) 网点约束,有 (15) 5) LGR积分的性能指标函数 用LGR积分近似性能指标函数 (16) (17) 经过上述变换后,最优控制问题转化为求解离散节点上的状态Xi和控制变量Uk,(i,k=1,…,K),以及初末时刻t0、tf(未给定),使得性能指标(7)最小,并满足动力学方程约束(1),终端条件约束(5),以及过程约束条件(6)的最优控制问题。 2.2 hp-RPM自适应策略设计 hp自适应方法根据网格的曲率和约束方程的误差判定自动调整网格数量和多项式阶次[11]。通过判断路径约束误差决定是否新增区间。在区间内通过判断轨迹的曲率来决定采用增加配点数的策略,还是增加多项式阶次的策略。设允许的最大误差为εmax,最大允许曲率为rmax,则误差和曲率比判据为: 1) 误差判据 (18) 式中,i=1,…,Nk为第k个子区间的第i个配点。 则该区间上的采样点在约束方程上的残差为: (19) (20) 2) 曲率比判据 (21) 于是,第l个状态在第p个采样点处的曲率为 (22) (23) (24) 因此,曲率判据为e 2.3 算法步骤 hp-RPM求解航空制导炸弹轨迹优化设计问题的步骤如下所示,其迭代流程如图2所示。 图2 hp-RPM迭代流程图 1) 初始化,给定初始状态x0,误差门限值εmax,选取K个区间,每个区间设定N个点; 4) 在局部残差最大值所对应的采样点上将区间进一步细化,新增区间配点数为N; 5) 若e 6) 所有子区间更新后,返回步骤2)。 3.1 仿真条件 初始条件: y(t0)=7 000 m V(t0)=240 m/s 终端条件: y(tf)=0 m V(tf)=220 m/s θ(tf)=-75° 过程约束: 120 m/s≤V≤340 m/s 3.2 仿真结果 根据上述条件,选取Vr=240 m/s,Lr=7 400 m代入(1)式的无量纲化模型,采用第2节的hp-RPM优化求解策略对制导炸弹轨迹进行优化,优化后的状态变量和控制变量曲线如图3所示。 图3 轨迹优化结果 其中,CM代表常规方法,Hamilton函数曲线如图4所示。为验证该增程效果,对其他不同初始条件下的轨迹快速优化问题进行了仿真,表1为在不同初始条件下经hp-RPM优化后和与常规方案相比的仿真结果。 图4 hp-RPM算法给出的Hamilton函数曲线 如图3a)所示,经hp-RPM优化后的曲线显得更加平缓光滑,特别是弹道的后半段,这样的安排,使得制导炸弹飞的更远。图3b)显示,两者在速度方面,常规方案的波动幅度要大,图3c)展示,两者的弹道倾角基本变化趋势基本一致,但优化后的方案速度变化更加平滑,图3d)~图3f)所示两者在弹道初始段和弹道末段的控制量相差较大,在30~100 s的中段两者基本一致,两者都满足了攻角、过载、攻角速率、终端速度、终端弹道倾角的约束,而优化后,制导炸弹的飞行时间由原来的180 s增加至195 s。另外,若终端时刻自由,由极小值原理可知,哈密尔顿函数应该保持为零,图4可知,哈密顿函数在10-5量级,在一定程度上说明了解的最优性。 该优化计算在CPU为3.3GHz/i5-4590,内存8G,Windows 7系统,Matlab环境下编程实现。算例中,优化的时间开销为1.14 s,而在Matlab环境下求解一个二维优化问题,一般需要30分钟。因此,hp-RPM在计算速度上具有很大的优势。 表1 不同初始条件下hp-RPM优化算法增程情况 从表1可知,经hp-RPM优化后制导炸弹的射程得到了较大的改善,均有不同程度的提高。其中在序号1和2的条件下,增程小于10%,这主要在于这2个初始条件的初始高度较高,制导炸弹滑翔段时间较长,占比整个弹道的比例较大,常规方案中俯冲攻击段使得飞行时间减少。在7 000 m高度,240 m/s速度投放,能够增程10.94%,而在180 m/s时能够增程8.42%,这是因为220 m/s的末端速度约束,迫使俯冲攻击段需要调整较大的角度,导致飞行时间减少。在5 000 m高度投放,最大可以增加17.37%的射程,增程比较明显。 综上,hp-RPM能在多约束条件下快速生成符合要求的轨迹,计算量小,计算精度高,适合于工程应用。 本文采用了一种基于hp自适应的Radau伪谱法对航空制导炸弹进行快速轨迹优化,首先建立了优化模型,将优化问题转换为NLP问题后,利用hp-RPM对其进行求解。仿真结果表明,在多约束条件下,该方法能够快速的生成符合要求的轨迹,Hamilton函数曲线表明优化结果满足一阶最优性条件,计算速度快,射程增加幅度平均达到11.46%。对多约束条件下的轨迹优化问题,具有一定的参考价值。 [1] 贾秋锐,孙媛媛,肖树臣,等. 航空制导炸弹发展趋势[J]. 制导与引信, 2014, 35(1): 8-11 Jia Qiurui, Sun Yuanyuan, Xiao Shuchen,等. Development Trend of the Aerial Guided Bomb[J]. Guidance & Fuze, 2014, 35(1): 8-11 (in Chinese) [2] 孙勇,张卯瑞,梁晓玲. 求解含复杂约束非线性最优控制问题的改进Gauss伪谱法[J]. 自动化学报, 2013, 39(5): 672-678 Sun Yong, Zhang Maorui, Liang Xiaoling. Improved Gauss Pseudospectral Method for Solving Nonlinear Optimal Control Problem with Complex Constraints[J]. Acta Automatica Sinica, 2013, 39(5): 672-678 (in Chinese) [3] 雍恩米,唐国金,陈磊. 基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J]. 宇航学报, 2008, 29(6): 1766-1772 Yong Enmi, Tang Guojin, Chen Lei. Rapid Trajectory Optimization for Hypersonic Reentry Vehicle via Gauss Pseudospectral Method[J]. Journal of Astronautics, 2008, 29(6): 1766-1772 (in Chinese) [4] Elnagar G, Kazemi M A, Mchen R. The Pseudospectral Legendre Method for Discretizing Optimal Control Problems[J]. IEEE Trans on Automatic Control, 1995, 40(10): 1793-1796 [5] 董春云,蔡远利. 高超声速再入飞行器轨迹优化算法评估策略[J]. 西安交通大学学报, 2016, 50(4): 28-34 Dong Chunyun, Cai Yuanli. An Evaluation Strategy of Trajectory Optimization Algorithms for Hypersonic Reentry Vehicle[J]. Journal of Xi′an Jiaotong University, 2016, 50(4): 28-34 (in Chinese) [6] Huntingtong G T, Benson D, Rao A V. Comparison of Accuracy and Computational Efficiency of Three Pseudospectral Methods[C]∥AIAA Guidance, Navigation and Control Conference and Exhibit, 2007: 1-25 [7] Gandhi M, Theodonu E. A Comparison between Trajectory Optimization Methods: Differential Dynamic Programming and Pseudospectral Optimal Control[C]∥AIAA Guidance, Navigation and Control Confesence, 2016: 1-6 [8] Rexius S L, Rexius T E, Jorris T L, et al. Advances in Highly Constrained Multi-Phase Trajectory Generation using the General Pseudospectral Optimization Software (GPOPS)[C]∥AIAA Guidance, Navigation and Control Confesence, 2013: 1-6 [9] 袁宴波,张科,薛晓东. 基于Radau伪谱法的制导炸弹最优滑翔弹道研究[J]. 兵工学报, 2014, 35(8): 1179-1186 Yuan Yanbo, Zhang Ke, Xue Xiaodong. Optimization of Glide Trajectory of Guided Bombs Using a Radau Pseudo-Spectral Method[J]. Acta Armamentarii, 2014, 35(8): 1179-1186 (in Chinese) [10] Guo T D, Li J F, Baotys H X, et al. Pseudospectral Methods for Trajectory Optimization with Interior Point Constraints: Verification and Applications[J]. IEEE Trans on Aerospace and Electronic Systems. 2013, 49(3): 2005-2017 [11] 王丽英,张友安,赵国荣. 改进的hp自适应网格细化算法及应用[J]. 弹道学报. 2013, 25(1): 16-21 Wang Liying, Zhang Youan, Zhao Guorong. Improved Hp-Adaptive Mesh Refinement Algorithm and Its Application[J]. Journal of Ballistics, 2013, 25(1): 16-21 (in Chinese) Rapid Trajectory Optimization for Air Guided Bomb Nie Cong1,2, Zhang Ke1,2, Zhang Minghuan1,2, Wang Pei1,2 1.School of Astronautics, Northwestern Polytechnical University, Xi′an 710072, China 2.National Key Laboratory of Aerospace Flight Dynamics, Northwestern Polytechnical University, Xi′an 710072, China According to the ballistic characteristics of the vertical attack by an aerial guided bomb, we optimize its trajectory and design the iterative variable-order solution strategy based on the hp-adaptive Radau pseudospectral method (hp-RPM) to rapidly optimize the glide trajectory under multiple constraints. The strategy allows for different orders of polynomial approximation in different intervals. We enhance the accuracy of the intervals by redistributing allocation points with the trajectory curvature. We iterate the redistribution of allocation points until their computational accuracy is acceptable to an error-tolerant degree. Then we simulate the rapid optimization of the trajectory of a certain aerial guided bomb. The simulation results show that the strategy can rapidly generate satisfactory trajectories under multiple constraints and that the Hamilton function of the solution satisfies optimal performance conditions. Compared with the conventional strategies, the trajectory optimized with our strategy is improved by an average of 11.46%. guided bomb; trajectory optimization; residual; hp-adaptive; Radau pseudospectral method 2016-09-04 国家自然基金(61502391)与航天支撑基金(N2015KC0121)资助 聂聪(1986—),西北工业大学博士研究生,主要从事飞行器导航、制导与控制的研究。 TJ761.5 A 1000-2758(2016)06-0963-06








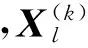




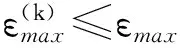
3 仿真算例与结果分析



4 结 论

