基于门限自回归模型的中国财政风险预警系统
孟庆斌 杨俊华
基于门限自回归模型的中国财政风险预警系统
孟庆斌 杨俊华
财政在整个宏观经济中占据着重要的地位,财政风险的出现往往对国民经济产生强烈冲击,甚至影响到社会的稳定。赤字风险是衡量财政风险程度的一个较好的尺度。在大部分时间里,我国赤字风险都较为平稳地处于中、低度风险状态。但在1999年到2003年的后东南亚金融危机时期,以及2008年之后的国际金融危机及经济转型时期,我国赤字风险程度都上升到了较高的水平。运用门限自回归模型可以较好地构建赤字风险预警系统,从而能够前瞻性地对赤字风险做出预警,采取相应对策化解或尽可能地降低财政风险。
财政风险预警;赤字风险指数;门限自回归模型
风险是经济生活中的核心问题,财政天生就是要承担公共风险的。同时,财政也是整个经济运行的总枢纽,一旦发生财政危机,必将会对国民经济产生强烈冲击,甚至影响到社会的稳定。由于特殊的发展阶段和所有制结构,与西方资本主义国家相比,我国财政还肩负着国有企业、国有银行“最后保护人”的角色,集各种风险于一身,更易受到冲击。自20世纪90年代以来,在改革不断深入以及国际经济危机此起彼伏的背景下,我国实行的积极财政政策,一方面使财政赤字不断攀升,债务规模持续增长,导致财政风险因素逐渐累积,另一方面又刺激了经济的高速增长,使财政收入连年持续稳定增加,国家抵抗财政风险的实力显著提高。夸大财政风险固然有害,低估财政风险则更为危险。在这种情况下,对我国财政风险的程度做出准确的度量,并且在此基础上对财政风险做出科学的预警,从而为政策的制定者提供充足的时间来制定预防措施,最大限度地降低财政危机的破坏程度甚至化解即将发生的危机,便具有重要的现实意义。
然而,2000年以前,相对于我国政府和国内学术界对金融风险和金融危机的关注和研究,关于财政风险尤其是其预警体系的探讨一直未引起足够的重视,研究成果比较匮乏。这样的情况随着1997年东南亚金融危机、2008年美国金融危机和欧洲主权债务危机的相继爆发而逐步得到改善。历次危机中,我国金融、经济系统均受到了极大的冲击。为应对实体经济的下行风险,1998年到2003年以及2008年至今,我国先后两次实施大规模经济刺激政策,加大政府投资,扩大债务融资规模。这样的政策虽然在一定程度上保证了经济增长,化解了国内经济危机的隐患,但大幅增加的财政赤字和国债余额,使财政风险不断累积。与此同时,为配合中央政府的经济刺激方案,地方政府的融资规模迅速扩大,或有负债大量增加,也使潜在的财政风险问题凸显出来。在此背景下,人们开始重新审视财政风险,我国政府和学术界也对财政安全问题更为关注。
一、财政风险的研究现状
在国际上,学者们在财政风险这一领域的研究多为国际比较,而由于不同国家之间情况相差较大,财政风险的度量无法采用相同的尺度,因此他们更加关注财政危机而不是财政风险。然而由于在实证研究当中,危机预警系统模型的构建需要较为充足的危机样本,但不同于金融危机(特别是货币危机),财政危机爆发在某种程度上说等同于国家破产,这种情况十分罕见(近年来,只有冰岛国家破产这个唯一的案例)。因此,学者们更多地将注意力集中在对主权债务问题*简单来说,主权债务是专指一国政府以外币发行债券形成的外债。的研究上,特别是致力于主权债务危机预警模型的构建。[1]
在我国,从本世纪初开始,财政风险问题虽然逐渐成为学界讨论的一个热门话题,出现了不少有价值的学术成果,但这些成果主要集中在财政风险的界定、表现形式、形成机理、影响因素、防范措施等问题的阐述,以及我国财政风险的理论框架和实证基础的构建上。目前针对我国财政风险预警系统的研究尚处于起步阶段,大多数研究成果的基本思路是通过设定一套尽可能全面反映经济、金融、政策、制度等状况的指标体系,采用指标对比分析法来判断财政风险的程度,这实际上并不是真正的财政风险预警系统。造成这一问题的原因在于,1994年我国确立了适应社会主义市场经济体制的税收制度和财政管理体制,使预算外资金规模比以前大幅度减少。但从1994年到目前时间区间较小,而且在此期间内我国财政指标的波动并不十分剧烈,因此构建财政风险预警系统有一定难度。同时,由于财政数据大多以年度数据为主,要想在时间区间不很长的情况下,保证足够的数据样本,就必须使用月度财政数据,然而,即使在统计制度健全、数据资料比较充分的发达国家,相关的月度财政数据也是很难获取的。因此,即使构建了财政风险预警系统模型,也存在所需数据短缺的问题。
鉴于以上问题,本文将选取合适的指标(兼顾与财政风险紧密相关性和数据可得性),借鉴国际学术界金融危机尤其是货币危机预警系统模型的设计方法,尝试构建与我国国情相适应的预警模型。在预警目标上,由于在我国历史上不存在财政危机的先例,因此本文主要对我国财政风险进行预警。在指标选取上,财政风险主要表现为赤字风险和债务风险[2],但由于我国目前公布的有关债务指标都是年度数据且很不完整,特别是地方政府债务数据几乎无从查证,因此,本文将主要尝试构建赤字风险预警系统。当然,有关财政赤字,目前官方公布的数据在个别月份也有所遗漏,本文只能根据公开的月度财政收支数据自行计算。在方法选取上,由于我国的数据样本较短,且指标波动较小,因此本文将采用非线性计量方法,尽量捕捉数据中的波动。
通过本文的研究,笔者试图在理论上提出比较完整的财政风险度量和财政风险预警的方法和体系,在较大程度上完善和发展我国关于该领域的文献和知识体系;在实践层面,能够为政策制定者提供一套较为准确而且具有较强可操作性的财政风险度量和预警方法,为其准确把握当前的财政风险状况,及时调整财政政策,最大限度地减轻乃至化解财政风险提供有效的工具。
本文剩余部分的安排如下:第二部分界定了赤字风险指数,并借助HP滤波方法对我国1994年1月到2015年9月间的赤字风险情况进行了定性描述;第三部分利用门限自回归模型测算出我国财政风险指数的两个阈值,以此对我国财政风险状况做出判断,并在此基础上构建我国财政风险预警模型;第四部分总结全文。
二、赤字风险的描述
一国财政风险主要由收入风险、支出风险、赤字风险和债务风险构成。[3]但是当收入支出协同变化时并不会引致过高的财政风险*也即财政收入和财政支出存在协整关系。[4],比如财政支出大幅提高可能是由于收入状况改善,资金充裕;财政收入减少也有可能是由于支出减少,或政府有意减轻企业和个人的税赋。只有当二者的变化失去协同性时才会导致赤字的急速增加,而政府为弥补赤字不得不通过发放国债的形式进行融资,使债务规模不断累积。当债务规模累积到一定程度,财政收入难以承担债务还本付息压力时财政风险便显现出来,因此对财政危机的刻画应主要着眼于赤字和债务层面。然而,由于我国目前公布的有关债务指标都是年度数据且很不完整,特别是地方政府的或有债务数据几乎无从查证,因此本文只能从赤字风险角度入手,对财政风险问题进行研究。当然,有关财政赤字的数据,目前官方公布的也仅是年度数据,笔者只能根据公开的月度财政收支数据自行计算。
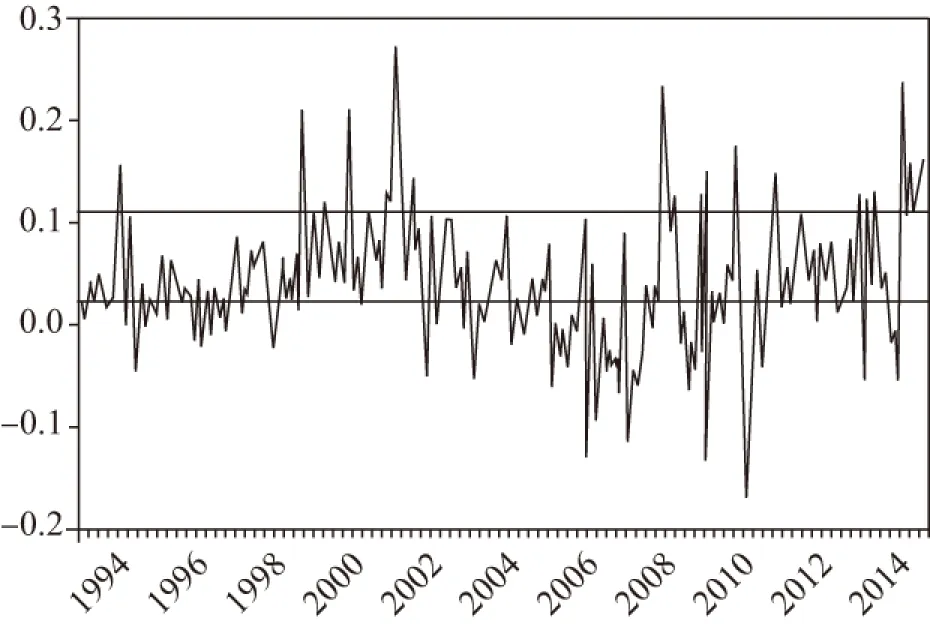
为了计算出月度财政赤字,本文首先找到月度财政收支数据。鉴于月度财政支出和财政收入具有较强的季节性,为考察这些序列的波动趋势特征,应消除这两个序列中的季节性。为此,本文首先对财政支出和财政收入数据进行X-12调整,然后做差,从而得到月度财政赤字数据。同时,由于我国官方公布的GDP数据为季度数据,因此本文采用通常做法,用工业增加值对其进行替代。同样,由于该序列中也存在着较为严重的季节性因素,因此本文也需要对其进行X-11季节调整。这些数据主要来源于中经网统计数据库。1994年1月到2015年9月间的赤字风险指数变化见图1。
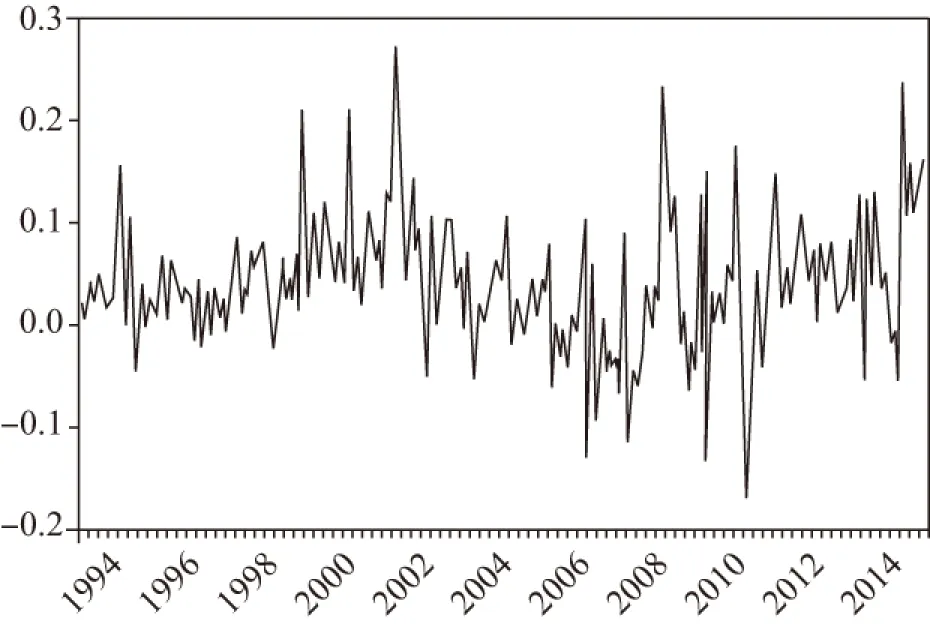
图1 赤字风险指数(1994年1月-2015年9月)
在对赤字风险指数进行实证研究之前,为了更加清晰地观察其变化趋势,本文对赤字风险指数进行HP滤波处理(见图2)。从图2可以看到,从1997年底开始,赤字风险指数开始走高,到2002年达到顶峰;此后,从2003年开始,我国财政风险状况逐渐得到改善,赤字风险指数一路走低,甚至在2006年和2007年一度跌至零点之下;但从2008年开始,财政风险指数又迅速触底反弹,并很快攀升至较高的水平。
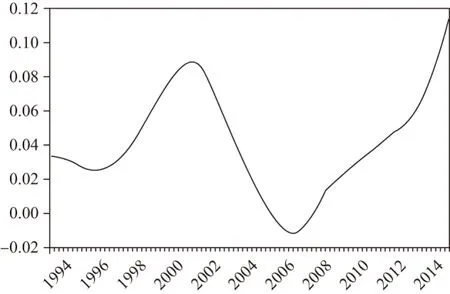
图2 赤字风险指数HP滤波趋势
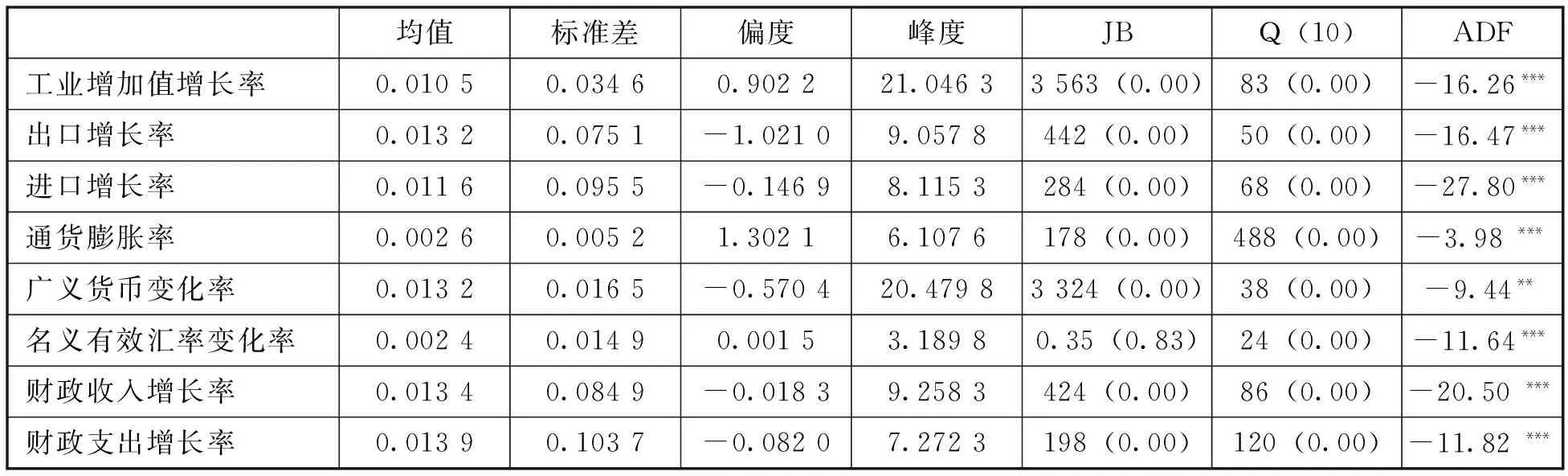
财政风险指数的基本统计特征见表1。从表1可以看到,赤字风险指数为平稳序列,且存在着较强的序列相关性(Q(10)=113.04)。但鉴于该序列在样本期内波动剧烈,峰度较高且JB统计量较大,表明其分布与正态分布相去甚远。这就说明,赤字风险指数序列可能存在着显著的结构性变化或结构性断点,或者说具有某种非线性特征。
表1 赤字风险指数基本统计特征(1994年1月-2015年9月)
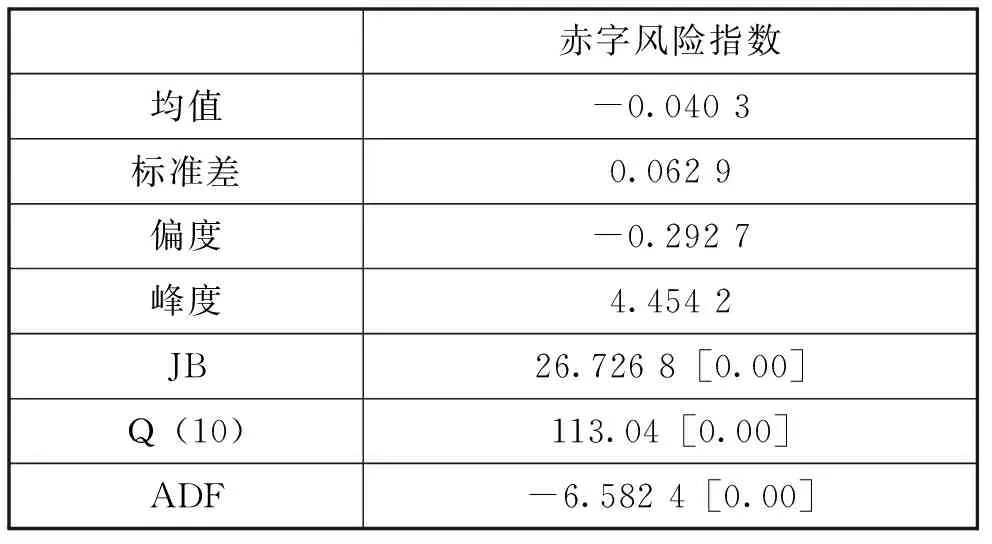
注:(1)JB为检验样本是否服从正态分布Jarque-Bera统计量;(2)Q(10)为检验时间序列中是否存在序列相关的Ljung-Box统计量;(3)ADF为检验各序列中是否存在单位根的Augmented Dickey-Fuller统计量,各统计量后面括号内数据为其p值。下文中与此相同。
作为一类非线性模型,门限自回归模型(Threshold Autoregressive Model,简称TAR)能够很好地解释经济数据中的非线性性质。该模型暗含了一个假定,即在某一特定的时点,时间序列的演进方式可以从一种机制(regime)跳跃到另一种机制,而且这种跳跃是离散的。这样,利用门限值就可以将一列非线性时间序列根据不同的机制划分为若干个线性子序列,进而对每个子序列分别进行估计。由此可见,门限自回归模型能够较好地对包含结构性断点的时间序列进行拟合,因此本文将利用该模型对我国赤字风险状态进行更加深入的研究。
三、财政风险识别与预警体系构建
本文将利用门限自回归模型测算出我国财政风险指数的两个阈值,并以此将我国财政风险状况划分为高度、中度和低度三类,在此基础上构建我国财政风险预警模型,并对其预警准确性进行评估。
(一)TAR模型简介
门限自回归模型最初由Tong和Lim[5]于1980年提出,但由于建立该模型的建模步骤比较复杂,在很长一段时间内未得到足够的重视,直到Tse在1989年提出了相对比较简易的建模及检验方法[6]后,才逐渐得到广泛应用。
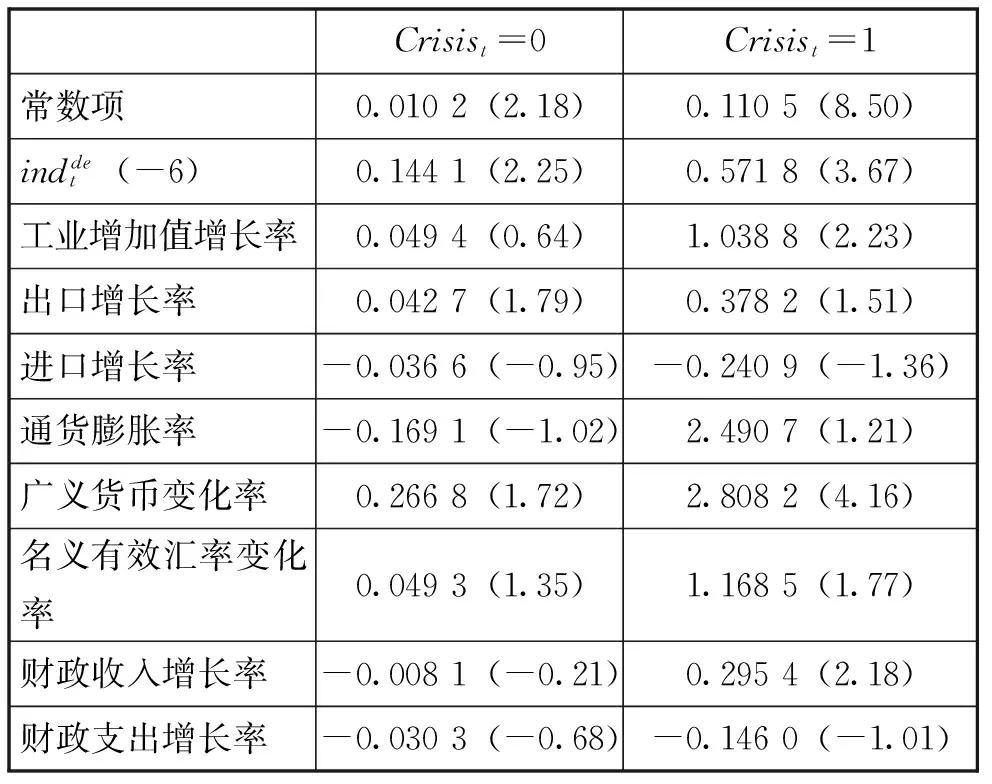
一般地,如果时间序列{Xt,t=1,2,…}满足Xt=ψj0+ψj1Xt-1+ψj2Xt-2+…ψjpjXt-pj+ξjt,rj-1 在实际应用中,Tong[7]以及Tong和Lim[8]提出了各种状态下涉及若干含有分离高阶AR(p)过程的TAR模型,其状态的一般形式可表示为: 这里存在由yt-1取值定义的两个可分离状态,α为TAR模型的阈值,由上式可以看到,在阈值上下时间序列特征发生了跳跃式改变。阈值α通常是未知的,本文将利用Chan[9]所提出的网格遍历方法来获得其超一致估计量。为保证每个区域内都有适当数量的观测值,本文将首先根据总体样本数量以及实际经济问题的需要,在检索中排除最高和最低部分一定比例的样本,作为阈值α的取值集合,然后在α的取值集合内进行遍历,逐一建立TAR模型,并选取使模型残差平方和最小的α作为TAR模型的阈值。 (二)财政风险识别模型 从表1中可以看到,对1994年1月到2015年9月间赤字风险指数数据进行平稳性检验可得其ADF统计量为-6.582 4,在1%的显著性水平下拒绝了该序列存在单位根的原假设。分别对其建立AR模型和TAR模型,参数估计结果见表2,其中第2列为AR模型估计结果,第3到第5列为TAR模型估计结果。 表2 财政风险指数序列参数估计结果 注:(1)***表示在1%的水平下显著,**表示在5%的水平下显著,*表示在10%的水平下显著;(2)R2为回归模型可决系数;(3)Log为回归模型最大似然值;(4)小括号内为T统计量。下文符号与此相同。 从表2可以看到,使用Chan的方法在数据中位数上下进行搜索,可得两个门限值分别为α1=0.106 1、α2=0.015 9,将超过α1的部分定义为高度风险状态,低于α2的部分定义为低度风险状态,二者之间的部分定义为中度风险状态。高、中、低度财政风险样本自回归参数估计结果分别见表2第3、4、5列。比较TAR模型和AR模型(见表2第2列)可以看到:在拟合优度上,与AR模型相比,TAR模型可决系数大幅提高。利用最大似然值构造LR统计量(似然比统计量,LR=2(Log3-Log1))得LR=20>x0.05=18.31,在5%水平下具有显著性,说明引入两个门限效应之后模型的拟合效果有了显著提高。同时将线性模型与仅存在一个门限的TAR模型相比可以看到,由于此时其最大似然值Log2=378,故有LR=2(Log2-Log1)=-8<15.09,也就是说,与线性模型相比,仅引入一个门限的TAR模型拟合效果并未产生显著的提高,因此具有两个门限的TAR模型更加合理。此外,AIC统计量也表明,两门限TAR模型效果更好(单门限TAR模型AIC统计量为-2.86)。赤字风险指数与门限α1、α2见图3。 图3 赤字风险指数及其TAR模型阈值 从图3可以看到,1994年1月到2015年9月间的大部分时间,赤字风险都处于中、低度风险状态。从1994年到1999年,赤字风险主要集中于中、低度风险状态,这也是我国当时成功实现宏观经济“软着陆”的成果。从1999年下半年开始,我国为了应对宏观经济不景气的趋势,采取了以增加财政支出、增发国债、扩大财政投资为主要措施的积极财政政策,赤字风险指数逐渐走高,进入高度风险状态,并一直持续到2003年。从2004年开始,我国经济逐渐转好,积极财政政策逐渐淡出,相应的赤字风险指数从2004年和2005年的中度风险状态转变到2006年到2007年的低度风险状态。在2006年到2008年上半年的很多月份里,财政风险指数已经为负,即我国已出现了财政盈余。然而,2008年国际金融危机的不期而至使我国经济迅速降温,并陷入不景气状态。为此,我国推出了“四万亿投资”财政刺激计划,此举对拉动经济起到了立竿见影的效果,但也引致了大量赤字,财政赤字风险迅速累积,并很快进入高度风险状态,且这种状态一直持续到本文所研究的样本终点2015年9月。 (三)财政风险预警模型 从广义上说,财政风险的表现形式多样,就本文所选择的以赤字风险指数度量的财政风险来说,有低度、中度、高度三种赤字风险状态,本文更为关注的是高度赤字风险。也就是说,本文所要构建的预警系统实际上是高度赤字风险预警系统。为此,本文定义变量Crisist表示在t年是否出现财政风险,即: 其中K为中、高赤字风险之间的门限。 构建财政风险预警模型的重要一步是选择预警指标,形成正确的预警指标体系。本文在选取指标时,主要遵循三个原则:一是密切相关性,二是全面综合性,三是数据可得性。*特别是数据可得性制约了本文对许多重要相关指标的选取,如内外部债务只有年度数据,数据频率过低,无法纳入本文的预警指标体系。由于赤字风险既受国家经济增长、宏观经济稳定以及财政收支等内部因素的影响,又受到来自外部的冲击,因此经过综合考虑并参考相关领域的研究成果,本文选择以下4类指标:(1)反映实体经济增长状况的指标,包括工业增加值增长率*由于我国GDP数据没有月度数据,因此本文用工业增加值代替GDP。、出口增长率、进口增长率;(2)反映宏观经济稳定和货币政策的指标,包括通货膨胀率*用同比CPI的变化率来度量通货膨胀程度。、广义货币变化率;(3)反映财政收支表现的指标,包括财政收入增长率、财政支出增长率;(4)反映开放经济下外部冲击影响的指标,主要是名义有效汇率变化率*Krugman建立第一代货币危机理论时提出,不可持续的财政政策导致外汇储备不断流失(参见P. Krugman.“A Model of Banlance of Payments Crises”. Journal of Money, Credit and Banking, 1979,11(3): 311-325);Burnside等指出,赤字的货币化可能引发汇率危机(参见Burnside, C., Eichenbaum, M., and S. Rebelo.“Prospective Deficits and the Asian Currency Crisis”. Journal of Political Economy, 2001, 109(6):1155-1197)。他们把财政赤字与外汇储备和汇率问题联系在一起,因此,本文就从相反的角度将外汇储备和汇率的变化作为财政赤字风险的预警指标。。 上述指标中,除广义货币和名义有效汇率外,其他序列都在原序列的基础上经过X-11季节调整。本文将预警时间窗取为6个月,其原因在于:一方面,预警时间窗与样本规模成正比,当样本较长时,时间窗也相应较长。*如Kaminsky等基于20个国家的25年数据,将预警时间窗口确定为24个月(参见Kaminsky, G. L., Lizondo, S., and C. M. Reinhart.“Leading Indicators of Currency Crises”. IMF Staff Papers 45, 1998);Oka则对118个国家17年的数据进行研究,他们的样本期为3年,但数据为年度面板数据(参见C. Oka.“Anticipating Arrears to the IMF:Early Warning Systems”. IMF Working Paper, WP/03/18, 2003)。本文仅对我国的情况进行研究,且如第二部分所述,由于受到数据可得性限制,以及政策变迁,本文所使用的样本从1994年开始,数据时间序列较短,再加上过去我国出现财政风险的样本较少,当预测窗口过长时,势必导致预警准确性大幅降低。因此,本文的预警时间窗不应超过一年。另一方面,根据郭庆旺等人的研究[10],我国宏观经济变量对财政收支的影响持续期在半年左右,因此提前6个月对财政风险状况做出预警,也使我们能够提前制定相关政策来防范并在一定程度上化解风险。综合以上两点,本文将预警时间窗的长度选为6个月。根据这一时间窗的选取,本文预警指标的时间区间为1994年7月到2015年9月。数据均来源于中经网统计数据库。这些序列的统计特征如表3所示。 表3 宏观经济变量基本统计特征(1994年1月-2015年9月) 表4 预警系统参数估计结果 注为赤字风险指数的滞后6期项。 运用1994年7月到2010年9月的样本建立门限自回归模型,得到K=0.080 3,由此可见,(3)式中Crisist的具体定义可表示为: 表5中的有风险和无风险表示某一时点赤字风险事实上是否进入高风险状态,而发出信号和不发出信号则表示该时点预警模型是否发出进入高风险状态的预警。从表5中可以看到,在19次财政风险样本中,本文所构建的预警模型做出了8次成功的预警,准确率达到42.11%。这虽然并不是一个很高的比例,但与国外学者样本外预测的结果*Kaminsky等的样本外预警准确性仅为4%(参见Kaminsky, G. L., Lizondo, S., and C. M. Reinhart.“Leading Indicators of Currency Crises”. IMF Staff Papers 45, 1998);Frankel和Rose的样本外预警准确性仅为8%(参见Frankel, J., and A. Rose.“Currency Crises in Emerging Markets: An Empirical Treatment”. Journal of International Economics, 1996(41): 351-366); Bussiere 和 Fratzscher的样本外预警准确性也仅为20%(参见Bussiere, M., and M. Fratzscher.“Towards a New Early Warning System of Financial Crises”. European Central Bank Working Paper Series, No.145, 2002)。相比,这样的结果已经可以接受。如果考虑到本文的数据样本远远少于以上所提到的国外文献,且训练样本中风险样本比例相对较低(21%),而预警样本中风险样本比例较高(33.33%),本文所构建的预警模型效果已经非常不错。此外,本文对无风险样本所作的预警准确率也达到65.83%,说明本文预警模型的“错杀”比率也是比较低的。从以上两个方面来看,本文所构建的预警模型是有效的。 表5 财政风险预警结果 发出信号不发信号有风险811无风险1427 (四)稳健性检验 为了对结论的稳健性进行检验,本文还测算了在选取不同预警时间窗口情况下的预警精度。在训练样本不变时,当选取9个月和3个月的预警时间窗口时,模型预警精度虽然略有变化,但总体变化在可以接受的范围内。 此外,当改变训练样本和预警样本时,如将训练样本选取为1994年7月到2009年9月,与之对应的预警样本变为2009年10月到2015年9月时,模型预警精度也并未出现大幅下降。 以上结果由于篇幅所限文中并未详细列示,感兴趣的读者可以向作者索取。这些结果说明,本文所建立的财政风险预警模型的结果是比较稳健的。 财政是整个经济运行的总枢纽,一旦发生财政危机,必将对国民经济产生强烈冲击,甚至影响到社会的稳定。由于特殊的发展阶段和所有制结构,与西方资本主义国家相比,我国财政更易受到冲击。但2000年以前,相对于国内外学术界对金融风险和金融危机的研究,财政风险尤其是其预警体系的探讨一直未引起学术界足够的重视,这一领域的研究成果相对比较匮乏。从本世纪初开始,由于积极财政政策实施过程中大量积累了财政赤字,政府特别是地方政府或有负债大量增加,加上全球金融危机带来的强烈外部冲击,我国财政风险有所显现,政策部门和理论界对财政风险的关注度迅速上升。但对财政风险的研究存在着风险样本较少和数据(尤其是债务数据)可得性差的问题。本文从财政赤字层面出发,构建赤字风险指数,利用门限自回归模型研究了我国从1994年1月到2015年9月间的财政风险状况,并构建了我国财政风险预警系统。 通过本文的研究可以看到:我国赤字风险存在着三个状态,分别为赤字风险指数高于0.106 3时的高度风险状态,低于0.029 1的低度风险状态,以及介于二者之间的中度风险状态。在1994年1月到2015年9月的大部分时间里,我国赤字风险都处于中度风险状态。从1994年到1999年,赤字风险主要集中于中、低度风险状态,这也是我国当时成功实现宏观经济“软着陆”的成果。从1999年下半年开始,我国为了应对宏观经济不景气的局势,采取了以增加财政支出、增发国债、扩大财政投资为主要措施的积极财政政策,赤字风险指数逐渐走高,进入高度风险状态,并一直持续到2003年。从2004年开始,我国经济逐渐转好,积极财政政策逐渐淡出,相应的赤字风险指数从2004年和2005年的中度风险状态转变到2006年到2007年的低度风险状态。在2006年到2008年上半年的很多月份里,财政风险指数已经为负,即我国已出现了财政盈余。然而,2008年国际金融危机的不期而致使我国经济迅速降温,并陷入不景气状态。为此,我国推出了“四万亿投资”财政刺激计划,此举对拉动经济起到了立竿见影的效果,但也引致了大量赤字,财政赤字风险迅速累积,并很快进入高度风险状态,且这种状态一直持续到本文所研究的样本终点2015年9月。 在赤字风险识别的基础上,本文选取预警指标构建了我国财政风险预警模型。本文首先将1994年2月到2010年9月的数据作为训练样本,得到预警模型参数,然后将2010年10月到2015年9月之间这五年的数据作为预警样本,对预警模型有效性进行评估。从预警效果来看,虽然本文所构建的预警模型面临着数据样本少,以及与预警样本相比训练样本中危机样本比例低的问题,但对危机样本的预警准确率仍达到35%,高于不少国外货币危机预警经典文献的样本外预警精度。同时,本文构建的预警模型对无风险样本所作的预警准确率达到65%,“错杀”比率也很低。从以上两个方面来看,本文所构建的预警模型是比较有效的。 [1] Manasse, P., Roubini, N., and A. Schimmelpfennig.“Predicting Sovereign Debt Crises”.IMFWorkingPaper, WP/03/221, 2003; C. Oka.“Anticipating Arrears to the IMF: Early Warning Systems”. IMF Working Paper, WP/03/18, 2003; Fuertes, A. M., and E. Kalotychou.“Optimal Early Warning Systems for Sovereign Debt Crises”. Working Paper, Cass Business School, City University London, 2005. [2] 王美涵:《中国财政风险实证研究》,北京,中国财政经济出版社,1999;刘尚希:《财政风险及其防范研究文集》,北京,经济科学出版社,2000;刘尚希:《财政风险及其防范问题研究》,北京,经济科学出版社,2004。 [3] 丛树海:《财政扩张风险与控制》,北京,商务印书馆,2005。 [4] 郭庆旺、吕冰洋、何乘才:《我国的财政赤字“过大”吗?》,载《财贸经济》,2003(8)。 [5][8] Tong, H.,and K. S. Lim.“Threshold Auto-regression, Limit Cycles and Cyclical Data(with Discussion of the Paper)”.JournaloftheRoyalStatisticalSociety, 1980, 42(3):245-292. [6] R. S. Tsay.“Testing Acid Modeling Threshold Autoregressive Processes”.JournaloftheAmericanStatisticalAssociation, 1989(84):231-240. [7] H. Tong.“On a Threshold Model”. In C. H. Chen(ed.).PatternRecognitionandSignalProcessing. Amsterdam: Sijthoff and Noordhoff, 1978;H. Tong.ThresholdModelsinNon2linearTimeSeriesAnalysis,Vol.21ofLectureNotesinStatistics. Heidelberg:Springer Verlag, 1983. [9] K. S. Chan.“Consistency and Limiting Distribution of the Least Squares Estimator of a Threshold Autoregressive Model”.TheAnnalsofStatistics, 1993(21):520-533. [10] 郭庆旺、贾俊雪、刘晓路:《财政政策与宏观经济稳定:情势转换视角》,载《管理世界》,2007(5)。 [11] Kaminsky, G. L., Lizondo, S., and C. M. Reinhart. “Leading Indicators of Currency Crises”. IMF Staff Papers 45, 1998. (责任编辑 武京闽) Early Warning System of Fiscal Risk in China Based on Threshold Autoregressive Model MENG Qing-bin,YANG Jun-hua (School of Business,Renmin University of China,Beijing 100872) Based on the fiscal red figure, we investigate the fiscal risk between January 1994 and September 2019 in China, and builds up an early warning system for fiscal crisis. Firstly, we define the index of deficit risk, and give a qualitative analysis of the situation of deficit risk of China by means of HP filtering. Secondly, with Threshold Autoregressive Model, we get two threshold values and divide the fiscal risk situation of our country in the sample studied by this paper into high, low and middle risk levels. Finally, we divide the data sample into training and forecast parts, and builds up the deficit identification model and Early Warning System with each of them respectively. The result shows that, the deficit identification model performs well in measurement of the deficit risk, and the Early Warning System of deficit risk also gets a good score when carrying through the out-sample forecast. early warning system of fiscal risk; deficit risk index; Threshold Autoregressive Model 国家社会科学重大招标项目“中国财政金融安全:预警机制与风险控制体系”(05&ZD008);中国人民大学校内项目“卖空机制、股价信息效率与知情交易”(2015030083) 孟庆斌:中国人民大学商学院副教授,博士生导师;杨俊华:中国人民大学商学院硕博连读生(北京 100872)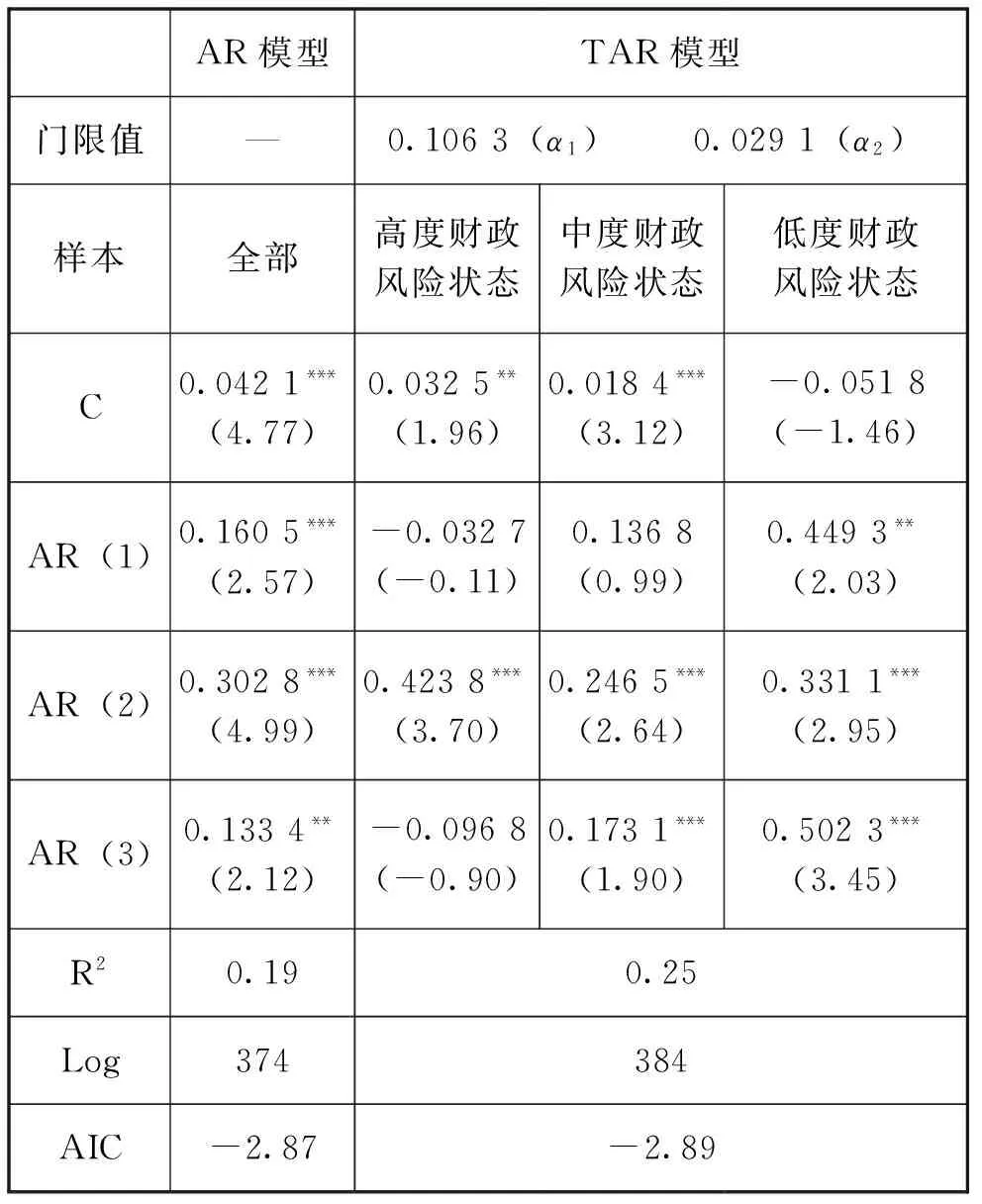
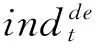

四、结论

