热声制冷微循环的特性优化

何秋石，吴锋，陈浩，田一泽，蒋智杰

武汉工程大学机电工程学院，湖北武汉430205

热声制冷微循环的特性优化

何秋石，吴锋*，陈浩，田一泽，蒋智杰

武汉工程大学机电工程学院，湖北武汉430205

建立包含直线过程的热声制冷微循环模型，简要描述了热声微循环过程.应用有限时间热力学的方法分析此模型的循环最优性能，求出了包含直线过程的热声微循环吸热与放热的临界点、循环的制冷量、制冷率及制冷机的性能系数；并由数值模拟得出热声制冷微循环中，制冷量、制冷率以及制冷机性能系数与直线过程压强比和等压过程体积比之间的特性关系.结果表明：制冷机的制冷量随着等压过程体积比的增大而增加；等压过程体积比给定的条件下，直线过程压强比越小的制冷机获得的制冷量就越大；适当的压强比或体积比可以有效的提高制冷机的性能系数.

热声制冷微循环；直线过程；有限时间热力学；制冷率；性能系数

1 引言

热声热机（或制冷机）［1］是基于热声效应原理的一种新型的热功转换装置.它用热声谐振取代机械压缩，使得它成为一种几乎没有（或少有）运动部件的热功装置；同时，与传统的热机相比，其基本机构简单可靠、寿命长、噪声低、无污染、发展方向明朗、应用前景广阔.热声热机所采用的气体工质可以认为是由无数微团构成的，它们通过与回热器管壁接触，然后发生热交换来完成热力循环.文献［2］对热声微循环进行了有限时间热力学分析，文献［3］分析了包含多变过程的内可逆Otto循环，文献［4］对包含多变过程的内可逆Lenoir循环性能进行了分析与优化，文献［5］和文献［6］分别对热力学中的多方过程与理想气体的直线过程进行了研究与分析.

在目前的热声微循环模型中，一般用两个等压过程和两个绝热过程（即布雷顿循环）来模拟气体微团的热循环，其循环的中间过程往往以“由于过程进行的太快，来不及与外界有显著热量交换，故将过程近似看作绝热过程”作为假设依据［7］.但实际上工质气体微团仍与热声叠流道器壁发生直接的热接触，不可能处于完全绝热的环境中.因此，用多变过程取代绝热过程与实际情况更加符合［8-12］.本文考虑用直线过程代替绝热过程来描述热声制冷微循环，并对其进行有限时间热力学分析，所得结果对于热声制冷系统的研究和运行有一定的实际指导意义.

2 循环模型

如图1所示，图1中过程4→1和2→3分别为定压吸热与定压放热过程，虚线过程3→N′→4和1→M′→2为理想条件下的绝热膨胀与绝热压缩过程；过程1→M′→2→3→N′→4→1是经典的热声制冷微循环［13］；过程1→M→2→3→N→4→1是本文提出的实际热声制冷微循环.

此模型下的热声制冷微循环如图2所示，该图表示了气体微团与回热器器壁之间的热作用过程：设初始状态时，气体微团（以下简称气团）在平衡位置处的平均温度为T0，平均压力为P0；ξm为气团的位移振荡幅值、Pm为压力振荡幅值、Tm为温度振荡值为纵向平均温度梯度；、分别为气团在多变过程中的温度波动值.如图所示，当气团处于管中间时（状态1）气团的温度为T0-.当气团在声压作用下历经一段吸热一段放热的多变过程1→2振荡到管右端（状态2）时，温度变为T0+Tm（即图1中的1→2过程）.此处气团周围的压力变为P0+Pm，与气团接触的管壁温度为T+ξ().此时，气团的温度是高于当地0m管壁温度的，会有热量Q23由气团流向管壁，放出热量的气团温度下降为T0+T3'（状态3）.这一过程即图2中的过程2→3（即定压放热过程）.图2中，过程3→4与过程1→2正好相反，气团历经多变过程振荡到管左端时，温度和压力分别变为T0-Tm、P0-Pm（状态4）.此时，气团的温度是低于管壁的温度T-ξ()的；所以有热量Q从管壁流向0m41气团，气团完成定压吸热过程温度升高到T0-（状态1）.气团回到初始状态，完成一个循环.

2.1 循环分析

此模型用两个直线过程代替理想条件下的两个绝热过程，能更加真实的反应热声制冷机的工作状况.图1中1→2→3→4→1循环所对应的状态参数为：温度Ti(i=1'2'3'4)且如图2所示气体微团在各个状态点参数的温度分别为压力对于多变过程1→2和3→4可以分别出直线方程

根据热力学第一定律以及理想气体状态方程，求出过程1→2中任一微小过程中的功dΑ、内能增量dΕ和热量dQ

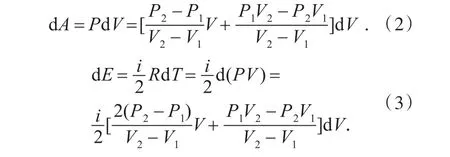
若假设热声制冷机的工质为氮气（双原子分子）可令i=5，

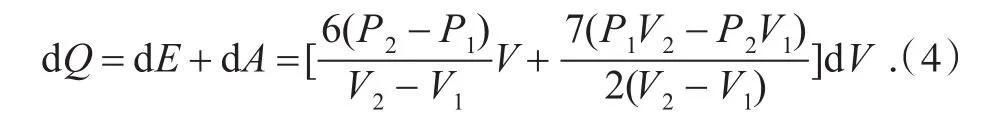
对于另一直线过程3→4，通过计算也可以得到吸，放热转换点N对应的体积和压强为

同理，过程4→1吸收的热量为

因为状态点1和状态点2以及状态点3和状态点4分别在两条绝热线上，故有

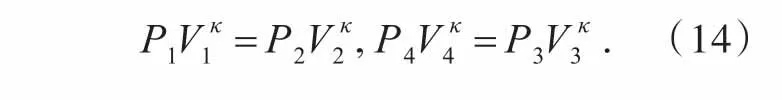
其中κ为比热比，由式（14）可得

则可以得到循环的吸热量和放热量分别为

将式（16）分别带入到式（7）、式（8）、式（10）、式（11）、式（12）、式（13）可得

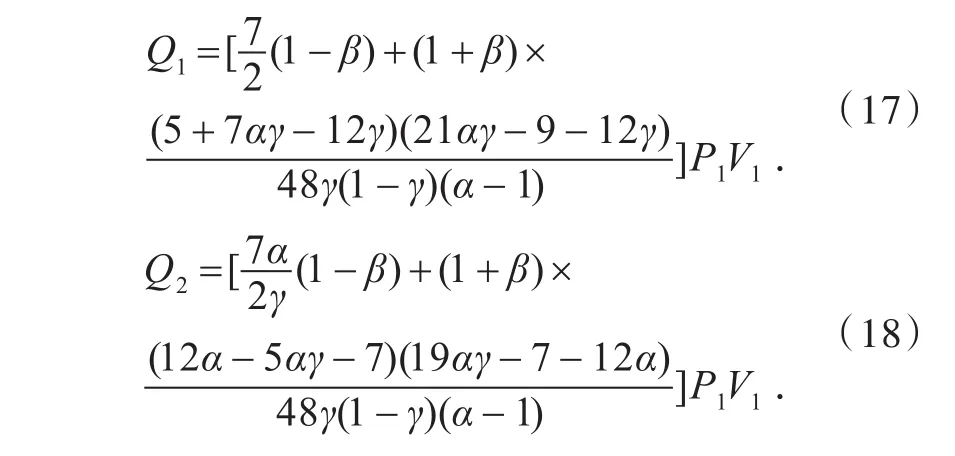
由于热弛豫，忽略两直线过程的历经时间，只考虑两定压过程（2→3和4→1）热量交换的时间，分别设为t23和t41.则循环的总时间τ为

若假设气体微团与固相工质之间的热交换满足牛顿线性导热定律，则定压放热过程2→3所放出的热量为

同理可以求得定压吸热过程4→1所历经的时间为

将式（21）和（22）代入到式（19）中可得循环时间为

在定压过程中，由于所设的惰性气体为理想气体，则由理想气体状态方程以及式（15）可得到

由于气体微团在各个状态点参数的温度分别为

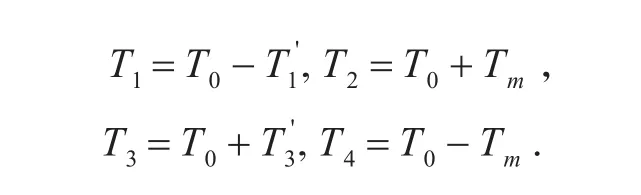
则可以进一步求得

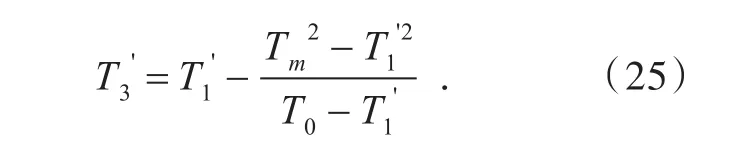
将式（25）代入（23）可化简为

2.2 循环优化

对于内可逆热声制冷机而言，其制冷量、制冷率以及性能系数应分别为

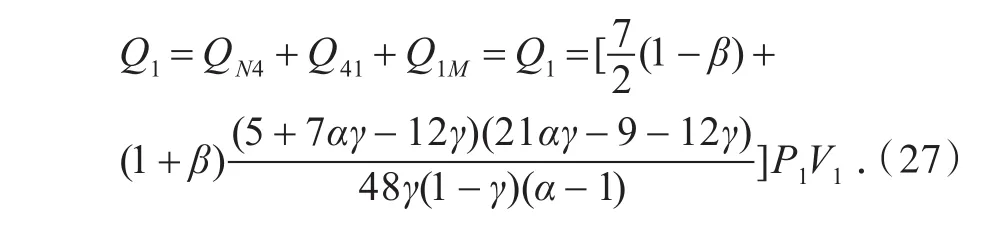
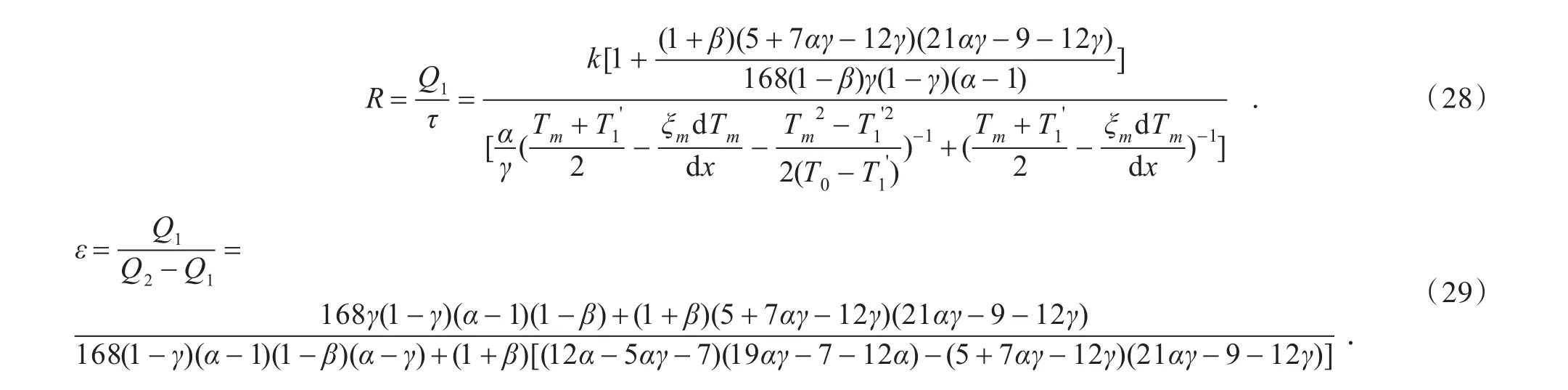
以制冷机的性能系数作为优化目标来对其进行优化［14-15］，因此对式（29）应用极值条件∂∂

ε γ=0，可以解得最佳性能系数对应的压强比γε'opt，将所求γε'opt代入式（27）和式（28）可得最佳性能系数条件下的循环制冷量Qγε'opt和制冷率Rγε'opt由于其解析解难以求出，可以由数值计算得到.

3 数值算例

根据文献［2］，取分子自由度i=5，平衡位置处的均温T0=300 Κ、均压P0=8 ΜΡa，温度振荡值Tm=50 Κ，状态点1温度波动值=35 Κ，位移振荡值ξm=0.05 m，纵向平均温度梯度600 Κ/m，状态点1和2之间的体积比（以下简称体积比）α的取值范围为(0.92～1)，若以压强比γ为变量，代入上面各式计算后，可得如下各参数之间的特性关系图.

图3 制冷量与压强比之间的特性关系Fig.3Characteristics relationship between refrigeration capacity and pressure ratio

由图3可知在内可逆热声制冷循环中，制冷量会随着压强比γ的增大而减小，当压强比趋近于1时，表明回热器内壁处于恒压状态，此时的制冷机已经失去意义，通过图3也可以看出此时的制冷量输出几乎为零.

从图4则可以得知制冷量随着体积比α的增大而增加，同时压强比γ越小，制冷机获得的制冷量就越大，这与图3所得结论也是吻合的.

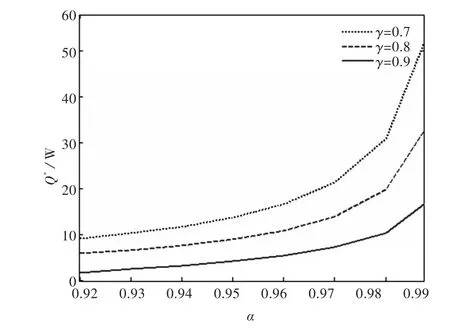
图4 制冷量与体积比之间的特性关系Fig.4Characteristics relationship between refrigeration capacity and volume ratio

图5和图6分别给出了制冷率和性能系数与压强比γ之间的特性关系图.由图5可知，制冷率与压强比γ之间的关系是基本呈单调递减的，随着压强比的增大，热声制冷系统的高压端压强与低压端压强之比就无限接近于1，系统内不存在压强差，制冷循环也就不存在了；而从图6可以得出，随着压强比γ的增加，性能系数先是呈递增状态，但压强比到达某一值时，性能系数不增反减，直至为0，可见必存在一最佳压强比γε'opt使得制冷机的性能系数达到最优.同时也可以看出体积比α对最佳性能系数的影响也是明显的，体积比越小的制冷循环，所对应的最佳性能系数也越大.故选择适当的压缩比与体积比来提高制冷机的性能系数是非常有必要的.

图5 制冷率与压强比之间的特性关系Fig.5Characteristics relationship between refrigeration rate and pressure ratio

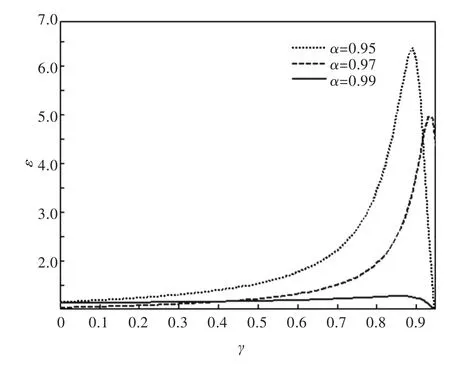
图6 性能系数与压强比之间的特性关系Fig.6Characteristics relationship between coefficient of performance and pressure ratio

4 结语

通过建立热声制冷微热力学循环模型，对循环的过程作出简要描述，利用有限时间热力学的方法，分析包含直线过程的微循环模型的最优特性，推导并求出直线过程的吸、放热的临界点所对应的压强与体积.由数值算例模拟得到热声制冷微循环中，制冷量、制冷率以及制冷机性能系数与直线过程压强比和体积比之间的关系曲线图，得出其优化解，对实际热声制冷机的改进与优化有一定的理论指导意义.

［1］吴锋，李青.热声理论的研究进展［J］.武汉工程大学学报，2012，34（1）：1-6.

WU F，LI Q.Advance in thermoacoustic theory［J］. Journal of Wuhan institute of technology，2012，34（1）：1-6.

［2］吴锋.斯特林机的有限时间热力学优化［M］.北京：化学工业出版社，2008.

［3］龚舒文，陈林根.包含多变过程的内可逆Lenoir循环性能分析与优化［J］.节能，2013（7）：22-26.

GONG S W，CHEN L G.Performance analysis and optimization of a Lenoir cycle with polytrophic process［J］.Energy saving，2013（7）：22-26.

［4］熊兵，陈林根.包含多变过程的内可逆Otto有限时间热力学分析［J］.电力与能源，2014，35（2）：166-171.

XIONG B，CHEN L G.Finite-time thermodynamic analysisofanendreversibleOttocyclewith polytrophic process［J］.Power and energy，2014，35（2）：166-171.

［5］吴文宜.理想气体直线过程的讨论［J］.大学物理，1996，15（7）：46-47.

［6］张忠厚.热力学中的多方过程研究［J］.辽宁工程技术大学学报（自然科学版），2006（25）：333-334.

ZHANGZH.Researchofpolytropicprocessin thermodynamics［J］.Journal of Liaoning technical university（natural science），2006（25）：333-334.

［7］SWIFT G W.Thermoacoustic engine［J］.The Jourmal of the acoustical society of America，1988（84）：1145-1180.

［8］赵忠明，李青.热声机械的研究现状及展望［J］.流体机械，2009，37（4）：79-82.

ZHAO Z M，LI Q.Study status and prospects of the thermoacoustic device［J］.Fluid machinery，2009，37（4）：79-82.

［9］张海伟，刘家林.热声制冷技术的研究与进展［J］.制冷，2012，31（3）：44-50.

ZHANG H W，LIU J L.Research and development of thermo-acousticrefrigerationtechnology［J］. Refrigeration，2012，31（3）：44-50.

［10］颜鹏，刘益才.热声热机的理论研究及其进展［J］.真空与低温，2011，17（3）：130-135.

YANP，LIUYC.Theoreticalresearchand development of thermoacoustic engines［J］.Vacuum &cryogenics，2011，17（3）：130-135.

［11］刘益才，武瞳.热声热机的研究进展［J］.真空与低温，2014，20（1）：1-8.

LIU Y C，WU T.Review of developments in the thermoacoustic engine［J］.Vacuum&cryogenics，2014，20（1）：1-8.

［12］郭方中，李青.热动力学［M］.武汉：华中科技大学出版社，2007.

［13］阚绪献，吴锋.热声热机微热力循环的最优性能［J］.武汉理工大学学报（自然科学版），2009，31（14）：130-133.

KAN X X，WU F.Performance optimization of a thermoacousticenginemicro-cycle［J］.Journalof Wuhan university of technology，2009，31（14）：130-133.

［14］陈浩，吴锋，林杰，等.变温热源条件下热声制冷机的火用效率分析［J］.化学工程与装备，2015，1（1）：10-13.

［15］林杰，吴锋，费锦华，等.实际热声热机微热力学循环性能优化［J］.湖北大学学报（自然科学版），2014，36（3）：233-237.

LIN J，WU F，FEI J H，et al.Performance optimization of an actual thermoacoustic engine micro-cycle［J］. Journal of Hubei university（natural Science），2014，36（3）：233-237.

本文编辑：陈小平

Optimizing Performance of Thermoacoustic Refrigeration

HE Qiushi,WU Feng*,CHEN Hao,TIAN Yize,JIANG Zhijie
School of Mechanical and Electrical Engineering,Wuhan Institute of Technology,Wuhan 430205,China

A thermoacoustic refrigeration micro-circle model with the straight line process was established and the process of thermoacoustic micro-circle was described briefly.The optimal performance of micro-circle was analyzed by using the finite time thermodynamics.The critical point of endothermic and exothermic,the refrigeration capacity,the refrigeration rate and refrigerator performance coefficient were calculated.The relationship between the refrigeration capacity,refrigeration rate and performance coefficient of refrigerator with the pressure ratio of straight line process and the volume ratio of isobaric process was obtained by using the numerical simulation.The results show that the cooling capacity increases with the volume ratio rising in isobaric process；the smaller pressure ratio of the refrigerator will obtain more refrigeration capacity at the given volume ratios of isobaric process；appropriate pressure ratio or volume ratio can improve the performance of the refrigeration.

thermoacoustic refrigeration micro-circle；straight line process；finite time thermodynamics；refrigeration rate；coefficient of performance

TK121

A

10.3969/j.issn.1674-2869.2016.06.012

1674-2869（2016）06-0577-06

2016-03-12

国家自然科学基金项目（51176143）；湖北省教育厅科研计划项目（Q20141506）

何秋石，硕士研究生.E-mail：895340997@qq.com

*通讯作者：吴锋，博士，教授.E-mail：wufeng@edu.cn