理想结构桁单元的开发及其应用*
裴志勇 郑培培 朱 波
(武汉理工大学高性能舰船技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063)
理想结构桁单元的开发及其应用*
裴志勇1,2)郑培培2)朱 波2)
(武汉理工大学高性能舰船技术教育部重点实验室1)武汉 430063) (武汉理工大学交通学院2)武汉 430063)
理想结构单元法(ISUM)以其高效、高精度而适用于大型结构系统的逐次崩溃分析.根据所受载荷的不同,将结构的变形形状理想化,从而开发出了系列理想结构板单元.对双层底纵桁的受力特点和变形特征进行分析,将其理想化开发出理想结构桁单元,并应用于1/13集装箱船模型在纯弯、纯扭和弯扭联合载荷作用下船体梁的逐次崩溃分析.将理想结构单元法计算结果与实验结构进行了对比分析.讨论了初始变形、焊接残余应力等初始缺陷对结构崩溃行为的影响.
逐次崩溃分析;极限强度;集装箱船;弯扭联合载荷;理想结构单元法(ISUM);理想结构桁单元
0 引 言
船体梁极限强度,也称为船体梁极限承载能力,对于保证船舶在极限状态如遭遇风暴、不当装载、不当卸载等状况下的结构安全性具有重要意义.其计算方法通常有简易方法如Smith法、非线性有限元法(NFEM),以及理想结构单元法(ISUM)等.简易方法做了一些假定,仅在一定条件下适用,如Smith法在船体受到纯弯作用时计算精度相对较高,对于弯扭联合载荷的情况,其精度尚需进一步深入的研究和验证.非线性有限元法在计算过程中要考虑材料非线性和几何非线性,要划分较细的网格才能达到精度要求,对于船体结构这样的大型结构体系,往往会因计算时间过长而难以在实际中应用.理想结构单元法将屈曲、屈服等非线性行为用适当的形函数理想化,对屈服准则等塑性条件理想化以避免沿板厚方向积分,并将这些理想化包含在单元中,这样就可以将较大的结构单位视为一个理想结构单元,从而大幅减少自由度,降低计算时间,使得对大型结构体系如船体梁等的极限强度分析成为可能.
按照理想化方法的不同,理想结构单元法的发展可分为三代[1].第一代理想结构单元法中屈曲变形不予考虑,屈曲后面内刚度的降低是通过有效带板宽度来考虑的[2];单元的非线性行为是通过理想化的解析公式来表达的,这样相应的公式相当复杂,只有具有相当的工程知识和数学力学理论功底的人才能理解其含义和解析过程.第二代理想结构单元法是将面外变形作为独立的自由度,以屈曲特征模态来理想化面外变形的形状[3];它将理想结构单元法的本质从如何精确地理想化非线性行为转变到如何选取有较少自由度的高精度的面外变形函数;单元精度取决于正确地选取变形函数来模拟实际的变形.由于在第二代理想结构单元法中采用屈曲特征函数,结构的屈曲行为能够较好的模拟;但对于极限强度以后的局部塑性变形(变形形状会迥异于屈曲特征模态),就不能很好的模拟了.第三代理想结构单元法采用崩溃模态的面外变形函数来模拟结构的逐次崩溃行为[4];基于非线性有限元的系列计算结果,用最小二乘法拟合出面外变形的形状函数,这样所开发的理想结构单元的精度能得以保证.根据结构所受载荷的不同,相应的面外变形函数也不相同,开发出了一系列的理想结构单元,如受纵向压缩和横向压缩的理想结构板单元,受面内弯曲作用的理想结构板单元[5],等参四边形理想结构板单元以及考虑水压作用和焊接残余应力影响的理想结构板单元等[6-8].
在研究中,先根据双层底纵桁所受载荷特点,进行系列非线性有限元分析,得到纵桁结构面外变形特征;然后理想化面外变形函数,进而开发出理想结构桁单元.随后,将开发的理想结构桁单元应用于1/13集装箱船模型,分析其在纯弯、纯扭以及弯扭联合作用下的逐次崩溃行为,并将计算结果与非线性有限元法计算结果和试验结果做比较分析,从而验证了所开发的理想结构桁单元的高效高精度特性.
2 理想结构桁单元开发
从第二代理想结构单元法开始,选取有较少自由度且能精确反映面外变形特征的形函数成为理想结构单元开发的核心.理想结构单元的开发流程见图1.

图1 理想结构单元开发流程
2.1 受剪切作用船底纵桁的非线性有限元分析
为了得到能精确表示剪切作用下纵桁的屈曲/屈服崩溃行为的变形函数,采用笔者开发的非线性计算程序系统“ULSAS”对典型纵桁结构进行了逐次崩溃分析,得到了不同载荷水平的结构变形形状,然后采用最小二乘法对变形形状进行拟合,可得到逐次崩溃过程中各分量的变化状况.对于一a×b×t=2 400 mm×800 mm×10 mm的典型板格,载荷及边界条件见图2.进行非线性有限元分析时,采用板单元来模拟,宽度方向划分为10个单元,长度方向网格大小跟宽度方向基本一致.在非线性分析过程中,板边假定一直保持直线.
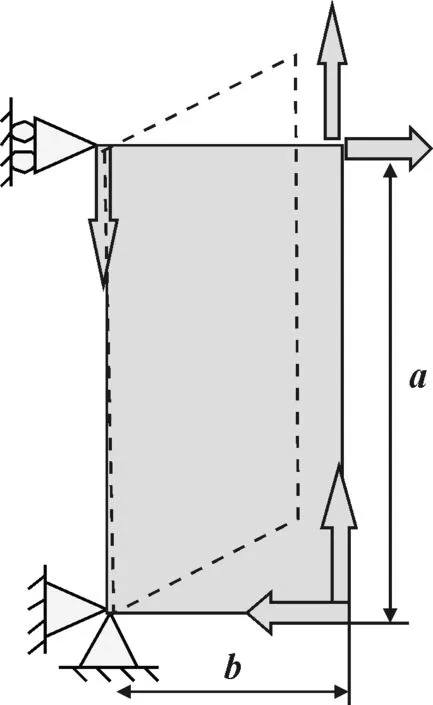
图2 剪切作用下板格载荷及边界条件

图3 各变形分量-剪切变形关系曲线
2.2 理想结构桁单元的面外变形函数
理想结构矩形板单元有4个节点,每个节点有3个自由度(u,v和wn),单元内部采用双线性插值.四边自由支持的矩形板划分为3个理想结构单元,见图4.纵向压缩下的面外变形幅值Al以及横向压缩下的面外变形幅值At分别作为独立于节点自由度的附加自由度.
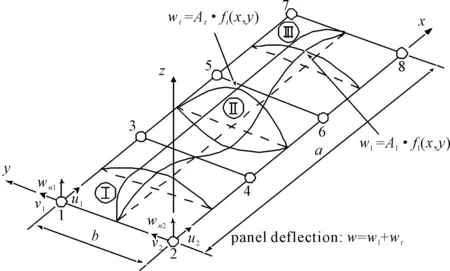
图4 理想结构矩形板单元模型
根据上节中典型板格在剪切作用下的非线性有限元分析结果,对于长为a、宽为b的矩形板格,剪切作用下其理想化面外变形形函数可表示为[9]
(1)
式中:m为剪切屈曲半波数;As为变形分量Am1(即纵向m个屈曲半波,横向1个屈曲半波)对应的变形幅值,将作为独立的自由度;ξi为各面外变形幅值A(m-1)2,A(m+1)2和A(m+2)1相对于Am1的变形幅值的比,其值可由非线性有限元计算结果得到.
根据非线性有限元计算结果,可用量纲一的量化的剪切应变来表示各面外变形幅值ξi,即
(2)


图5 A(m+2)1项系数ξ3对应的mi和pi值
为了模拟纵桁在面内弯曲作用下的崩溃行为,面内弯曲作用下纵桁面外变形的形函数为
(3)
式中:hdb和b分别为纵桁的高度和宽度,第i阶变形幅值Ai作为一个独立的自由度.理想结构单元划分和变形函数见图6.

图6 面内弯曲作用下纵桁理想结构单元划分及变形函数示意图
如果节点位移采用通常使用的双线性插值,则面内弯曲作用下板单元的变形是如图7a)所示的形状,这与实际的变形(见图7b))形状不符,会导致所谓的“剪切锁定”现象,即弯曲刚度变得过大.为了克服这个问题,在2个正交方向分别增加2个附加自由度Bx和By(见图7b),这样就能得到正确的节点位移和面内变形.

图7 面内弯曲下板单元的变形
对于实际的船底纵桁结构,会受到面内弯曲和剪切的双重作用,其理想化面外变形函数可表示为面内弯曲作用下的变形函数和剪切作用下的变形函数之和,即
w=ws+wb=

(4)
式中:As为剪切面外变形自由度;ξi为各面外变形系数;Ai为面内弯曲变形自由度.
2.3 理想结构桁单元计算公式的推导
在确定了理想结构桁单元面外变形函数w之后,就可以推导出其应变增量来,面内应变的线性项和曲率可以像常规的有限板单元一样来推导,面内应变的非线性项可通过弹性大变形分析(elastic large deflection analysis, ELDA)得到,即满足大变形时的变形协调条件
(5)
式中:F为Airy应力函数;w0为初始挠度值,采用与总挠度相同的表达式.解出Airy应力函数F之后,可得到大变形产生的非线性面内应力和应变,即
(6)
为了避免沿厚度方向积分,采用基于单位宽度力和弯矩的Egger屈服函数.在板单元的长度和宽度方向采用梯形积分法进行数值积分,每个理想结构板单元取7×7=49个积分点,在每个积分点根据Von Mises 屈服准则判断是否发生屈服.
总纵弯曲产生的节点挠度wn对面内变形的非线性影响,通过修正的Green应变增量来考虑.因此,总应变增量可表示为
(7)
式中:右边第一项为线性项,第二项为计及弹性大变形的非线性项,第三项为考虑整体屈曲的非线性项,采用改进的Green应变增量来表示.
对理想结构桁单元,运用虚功原理,可得以下增量形式表达式
KΔd=ΔF+(F-R)
(8)
式中:K为切向刚度矩阵;Δd为位移增量;F和ΔF分别为外载荷及其增量;R为内力.单元刚度矩阵及力向量可采用跟传统有限元方法相同的方式进行组集,得到总体刚度矩阵和力向量.
3 理想结构桁单元精度验证
为了验证所开发的理想结构桁单元的精度,对长a×宽b为2 400 mm×800 mm、厚度t分别为15 mm和20 mm的矩形板应用非线性有限元法和开发的理想结构单元进行了剪切作用下的逐次崩溃分析,得到的平均切应力-平均切应变的关系见图8.图中纵坐标为量纲一的量化的平均切应力τ/τY,横坐标为量纲一的量化的平均切应变γ/γY.对于板厚为15 mm的板,量纲一的量化平均切应变γ/γY=1.05和3.14时的崩溃模态比较见图9.理想结构单元计算结果,包括平均切应力-平均切应变关系曲线,以及不同切应变时的崩溃模态,均与非线性有限元计算结果保持一致.

图8 剪切作用下理想结构单元和非线性有限元计算结果比较

图9 剪切作用下非线性有限元(FEM)和理想结构(ISUM)单元崩溃模态比较
另外,还对长a×宽b为2 400 mm×800 mm、厚度t分别为15 mm和20 mm的矩形板在面内弯曲和剪切联合作用下的逐次崩溃行为用非线性有限元法和开发的理想结构单元法进行了比较分析,得到的量纲一的量化弯矩-切应力关系曲线,见图10.理想结构桁单元计算得到的载荷路径曲线跟非线性有限元计算结果能较好的吻合.

图10 弯剪联合作用下理想结构单元和非线性有限元计算结果比较
4 集装箱船模型逐次崩溃分析
为把握超巴拿马型集装箱船在纯弯、纯扭,以及弯扭联合作用下的逐次崩溃行为,Tanak等[10]进行了1/13缩尺的三舱模型崩溃实验.在本节中,运用开发的理想结构单元,对实验模型进行纯弯、纯扭,以及弯扭联合作用下的逐次崩溃分析,并将理想结构单元计算结果跟实验结果和LS-DYNA非线性分析结果进行了比较分析.
4.1 集装箱船模型
缩尺比为1/13的超巴拿马型集装箱船模型有3个由水密横舱壁分隔开来的舱室,每个舱室在其中部有抗扭箱结构以增强其总体抗扭能力,最前端和最后端的半个舱段设有中间甲板.最尾端面通过系列螺栓固定在刚性壁面上,在首部左右舷通过加载设备给模型施加载荷,通过调整左右舷载荷P1和P2的大小和方向来实现模型纯弯、纯扭,以及弯扭联合载荷状况,见图11.

图11 单元划分及加载装置示意图
用高效高精度理想结构单元来模拟集装箱船模型主要纵向强力构件,如船底板、内底板、舷侧外板、内壳板和甲板等在纯弯、纯扭,以及弯扭联合作用下的逐次崩溃行为.其余的构件,如横舱壁、抗扭箱等结构,对船体梁的弯曲及扭转崩溃基本上没有影响,用弹性有限元来模拟.板材用等参板壳元模拟,加强筋用弹性梁-柱单元模拟,在这2种单元的刚度矩阵中都考虑了几何非线性影响[11-12].模型中总共有3 369个理想结构板单元,1 790个弹性梁-柱单元和1 631个等参弹性板单元,网格划分及加载装置示意图见图11.
4.2 逐次崩溃分析
当图11所示的2个力大小相等且方向都向下时,即P2=P1,相当于在模型上施加纯弯载荷.需要注意的是,采用这种悬臂梁末端加载的方式,在横断面上会产生垂向剪力,严格意义上来说,这种情况并不是纯弯工况.当2个外力大小相等但方向相反时,即P2=-P1,相当于在模型上施加纯扭载荷.而当P2=-0.68P1时,模型则处于弯扭联合的状态,此时垂向弯矩与转矩的比值为0.5.
另外,在进行逐次崩溃分析时,还在理想结构板单元内考虑了焊接残余应力和初始缺陷的影响.根据该模型试验资料,初始变形为正弦屈曲模态,变形幅值取1%板厚;试验时测得模型的焊接残余应力大致为61 MPa(压缩应力σc),将此焊接残余应力加到理想结构板单元上,焊接残余应力分布见图12.

图12 焊接残余应力分布示意图
通过加载设备,在模型端部加载点位置施加强制位移,从而获得非线性载荷和载荷作用点位移的关系曲线.对于复合载荷情况,可采用跟试验相同的方式施加强制位移,使P2=-0.68P1,来实现垂向弯矩与转矩比值1∶2的弯扭联合工况.
4.3 计算结果及讨论
4.3.1 纯弯工况
采用理想结构单元法共计算了纯弯作用下不考虑焊接残余应力和初始变形影响、考虑初始变形但不考虑焊接残余应力影响和考虑焊接残余应力和初始变形影响这3种工况,计算得到的载荷与载荷施加点位移的关系曲线跟试验结果以及非线性有限元计算结果比较见图13.标示“ISUM_no ini_no wr”为理想结构单元法不考虑初始变形和焊接残余应力时的计算结果;“ISUM_ini_no wrs”为理想结构单元法考虑初始变形但不考虑焊接残余应力时的计算结果;“ISUM_ini_wrs”为理想结构单元法在考虑初始变形和焊接残余应力时的计算结果;“FEM”为采用LS-DYNA在不考虑初始变形和焊接残余应力的情况下进行的非线性有限元分析结果;“Pdown-P(exp.)”为试验时左舷施加载荷和载荷作用点位移关系;“Pdown-S(exp.)”为试验时右舷施加载荷和载荷作用点位移关系.在用理想结构单元法和非线性有限元计算计算时,所施加的载荷P1和P2是大小相等且方向相同的,所得到的载荷作用点的位移也是一样的.但在逐次崩溃试验时测得的载荷作用点的位移有少许差异,这是由于实际试验模型初始变形和焊接残余应力左右舷是不对称的,最终导致载荷作用点的位移在左右舷不完全一致,也就是说试验结果曲线左右舷的载荷-载荷作用点位移曲线是不重合的.

图13 纯弯工况载荷-载荷作用点位移关系图
采用理想结构单元法,考虑焊接残余应力和初始变形影响时,主要纵向构件在极限强度时的变形模态见图14,船底板在极限强度前、极限强度时和极限强度后的变形模态见图15.由于理想结构单元较大无法显示出单元内部变形情况,图14~15显示的都是虚网格,即一个理想结构单元用6×6的虚网格来显示单元内部的变形.

图14 纯弯工况极限强度时主要纵向构件变形模态

图15 纯弯工况不同载荷水平时船底板变形模态
对于考虑初始变形但不考虑焊接残余应力的情况,在首端两大小相等方向垂直向下的载荷作用下,甲板结构受拉且底部及内底结构受压.当载荷增加到约350 kN时,船底板率先发生屈曲,屈曲后理想结构单元法得到的船体刚度比非线性有限元法要稍低一些,这是由于当前的理想结构单元法中没有考虑加强筋对板的作用,从而使得板格的屈曲强度稍小.随着载荷的逐步增加,屈曲从尾部固定端向船首方向扩展,不仅底板发生屈曲,内底板和舷侧外板也发生屈曲并向首部扩展.当载荷增加到约550 kN时,靠近尾部固定端的船底板和舷侧外板靠近底板位置发生屈服;随着载荷的增加,屈服向船首部扩展.当载荷增加至610 kN时,甲板、甲板纵骨以及舷顶列板及其骨材受拉发生屈服;同时船底板和内底板及船底纵骨、内底纵骨受压发生屈服.随着屈服的扩展,整个结构不再能承受载荷,也就是说达到了极限强度状态.极限强度之后,塑性变形集中在尾端部(弯矩最大)区域,并且随着塑性变形的进一步发展,承载能力随之下降.
采用理想结构单元法进行分析时,当初始变形和焊接残余应力都不考虑时,模型崩溃过程中几乎没有屈曲现象发生,极限强度值较其它情况要大,且极限强度以后承载能力基本保持不变;考虑初始变形影响而不考虑焊接残余应力作用时,有屈曲现象发生而且极限强度以后承载能力会显著降低;而当同时考虑初始变形和焊接残余应力作用时,结构的初始刚度降低,在较低载荷水平下发生屈曲,极限强度较上述两种情况要小很多,极限强度以后有承载能力降低,但不是很明显.
非线性有限元计算是在考虑初始变形但忽略焊接残余应力的前提下进行的,同等条件下的理想结构单元法计算结果(图13中标示“ISUM_ini_no wrs”)跟非线性有限元计算结果吻合较好,但屈曲发生较早,这是由于理想结构板单元在计算屈曲时没有考虑加强筋对其的扭转作用所致.
考虑焊接残余应力影响的3个工况(理想结构单元、试验左舷和试验右舷)的计算结果跟不考虑焊接残余应力的3个工况(理想结构单元考虑初始变形、理想结构单元不考虑初始变形和非线性有限元)的结果相比,初始刚度稍低、屈曲发生较早且极限强度值要小.模型焊接施工时在焊接线附近产生较大的拉伸残余应力,而相应的在板格中间产生较大的压缩残余应力.在没有施加载荷之前,在该焊接残余应力的作用下板格会发生屈曲,所以考虑焊接残余应力作用时初始刚度较不考虑焊接残余应力时要稍低一些.由于焊接残余应力作用在板中间产生较大的压缩残余应力导致板格容易发生屈曲,进一步降低了面内刚度,同时弯曲引起的拉压应力与焊接残余应力合成导致屈服发生得较早,从而极限强度值较不考虑焊接残余应力作用时要小很多.
试验崩溃模态见图16,崩溃发生在最尾端舱室船底板的中央位置,崩溃后局部塑形变形都集中在此位置.理想结构单元法计算得到的崩溃位置与此相同,也在最尾端舱室船底板的中央,见图15b),c).

图16 纯弯试验时船底板崩溃模态
4.3.2 纯扭工况
理想结构单元法考虑和不考虑焊接残余应力、非线性有限元计算以及试验得到的载荷与加载点位移的关系见图17.标示“Pdown”为右舷载荷与加载点位移关系,因为该处的载荷是向下的;“Pup” 为左舷的结果,该处的载荷向上.在不同载荷水平下理想结构单元法考虑焊接残余应力影响时的变形模态见图18.为显示变形模态,图中是以虚网格形式表示的,即一个理想结构单元用6×6的虚网格来显示单元内部的变形.

图17 纯扭工况载荷-载荷作用点位移关系图
由理想结构单元法计算得到的纯扭工况船体梁的逐次崩溃过程如下:首先,剪切屈曲发生在板厚较薄的舷侧外板中部和内壳板的中部.随后,右舷尾部靠近船底位置板格由于纵向压力和剪力联合作用发生屈曲.随着载荷的进一步增加,中间舱右舷附近的舷侧外板和船底板发生崩溃,继而整体结构发生崩溃,达到极限强度状态.

图18 纯扭工况不同载荷水平时变形模态
在崩溃试验中,除了上述的崩溃模态外,还有两种其他崩溃模态,即舱口角隅的崩溃和甲板与舷侧外板间焊缝的崩裂.试验中出现的舱口角隅的崩溃和甲板与舷侧外板间焊缝的崩裂模态,不能用理想结构单元法模拟,因此试验结果较理想结构单元法结果(考虑焊接残余应力工况)要稍小.另外,利用LS-DYNA进行的非线性有限元分析是在不考虑焊接残余应力的条件下进行的,跟相同条件下理想结构单元法结果相比,非线性有限元计算的极限强度值稍低一些,但二者有着相同的趋势,大体上吻合较好.
4.3.3 弯扭联合工况
为了探究弯扭联合作用下的逐次崩溃行为,对P2=-0.68P1载荷条件下(垂向弯矩和转矩的比为0.5),采用理想结构单元法和非线性有限元法分别进行了逐次崩溃分析,并将计算结果与试验得到的载荷与载荷作用点位移关系比较见图19.跟纯扭工况类似,“Pdown”表示右舷载荷与加载点位移关系,因为该处的载荷是向下的;“Pup” 表示左舷的结果,该处的载荷向上.

图19 弯扭联合工况载荷-载荷作用点位移关系图
在不考虑焊接残余应力的前提下,理想结构单元法计算结果跟非线性有限元法计算结果吻合较好.同时,考虑焊接残余应力影响的理想结构单元法计算结果跟崩溃试验结果也吻合较好.
理想结构单元法计算得到的弯扭联合下的崩溃模态与纯扭状态的崩溃模态类似,但舷侧外板靠近底部板格屈曲发生得更早且变形值要大些,这是因为弯扭联合工况下该部位受到弯曲作用引起的压缩载荷较纯扭工况要大得多,从而引起该部位较大的变形和较早发生屈曲.
由于在本节计算时,垂向弯矩比转矩小得多,仅仅是转矩的一半,所以典型的崩溃行为与纯扭工况的典型崩溃行为几乎一样.
从上述计算结果可以看出,文中所开发的理想结构单元可以较准确的模拟纯弯、纯扭以及弯扭联合作用下集装箱船模型的逐次崩溃行为.
5 结 论
1) 基于非线性有限元计算结果,理想化剪切作用下面外变形函数,将其与面内弯曲作用下理想化变形函数一起构成理想结构桁单元的面外变形函数.
2) 通过板格在剪切及弯剪组合情况下与非线性有限元计算结果的比较,初步验证了所开发理想结构桁单元的精度.
3) 焊接残余应力对模型逐次崩溃行为的影响较大,考虑焊接残余应力的作用会导致较小的初始刚度和较低的极限承载能力.
4) 用理想结构桁单元进行了集装箱船模型在纯弯、纯扭和弯扭联合作用下的崩溃分析,验证了理想结构桁单元对大型结构系统逐次崩溃分析的适用性.
5) 通过理想结构单元的计算结果跟非线性有限元结果和试验结果的比较分析,验证了所开发理想结构桁单元的高效高精度特性.
[1]UEDA Y. Official discussion on “report of special task committee vi.2: ultimate hull girder strength”[C]. Proc ISSC 2000,Nagasaki, Japan,2000.
[2]UEDA Y, RASHED S. The idealized structural unit method and its application to deep girder structures[J]. Computers and Structures,1984,15:277-293.
[3]MASAOKA K, OKADA H, UEDA Y. A rectangular plate element for ultimate strength analysis[C]. Second International Conference on Thin-Walled Structures,1988:469-476.
[4]FUJIKUBO M, KAEDING P. New simplified approach to collapse analysis of stiffened plates[J]. Marine Structurers,2002,15:251-283.
[5]ISHIBASHI K, FUJIKUBO M, YAO T. Collapse analysis of ship’s double bottom structures with isum[C]. Proc of Int Conf on Computational Methods in Marine Engineering,2007:59-62.
[6]PEI Z, YU J, NAKAMARU K, TANAKA S, et al. Development of isoparametric ISUM plate element[J]. Int J Offshore and Polar Eng,2010(4):781-788.
[7]FUJIKUBO M, KAEDING P, OLARU D, et al. Development of ISUM plate element considering lateral pressure effects and its application to stiffened plates[J]. Transactions of the West-Japan Society of Naval Architects,2005,97:25-35.
[8]PEI Z. Progressive collapse analysis of ship hull girder using idealized structural unit method[D]. Hiroshima: Hiroshima University,2005.
[9]PEI Z, TAKAMI T, GAO C, et al. Development of ISUM shear plate element and its application to progressive collapse analysis of plates under combined loading[J]. Int J Offshore and Polar Eng,2010(4):773-780.
[10]TANAKA Y, ANDO T, YAO T, et al. Longitudinal strength of container ships under combined torsional and bending moments[J]. Int J Offshore and Polar Eng,2009(4):748-755.
[11]PEI Z,IIJIMA K,FUJIKUBO M,et al. Collapse behaviour of a bulk carrier under alternate heavy loading conditions[J]. Int J Offshore and Polar Eng,2013,23:224-231.
[12]PEI Z,IIJIMA K,FUJIKUBO M,et al.Simulation on progressive collapse behaviour of whole ship model under extreme waves using idealized structural unit method[J].Marine Structures,2015,40:104-133.
Development of ISUM Girder Element and Its Application
PEI Zhiyong1,2)ZHENG Pei2)ZHU Bo2)
(KeyLaboratoryofHighPerformanceShipTechnologyofMinistryofEducation,WuhanUniversityofTechnology,Wuhan430063,China)1)(DepartmentsofNavalArchitecture,OceanandStructuralEngineering,SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)2)
Idealized Structural Unit Method (ISUM) is suitable for progressive collapse analysis of large scaled structural system due to its high efficiency and sufficient accuracy. Series idealized structural unit elements are developed by idealizing lateral deflection which shall be different with different load. In the present research, the characteristics of load and deformation of girder in the double bottom structure are studied firstly. Then, the idealized structural girder element is developed. The developed element is applied to 1/13-scaled container ship model to perform the progressive collapse analysis under pure bending, pure torsion and combined bending and torsional moment. The influence of initial deflection and welding residual stress on structural collapse behaviour is discussed.
progressive collapse analysis; ultimate strength; container ship; combined bending and torsional moment; idealized structural unit method; ISUM girder element
2016-10-18
*教育部留学归国人员科研启动基金项目资助
U663.2
10.3963/j.issn.2095-3844.2016.06.003
裴志勇(1974—):男,博士,副教授,主要研究领域为船体梁极限强度

