纵连板式轨道在墩台位移作用下梁轨相互作用规律研究

刘 成，李 帅，谢铠泽，田春香，王 平

(1.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；2.中铁二院工程集团有限责任公司，成都 610031)



纵连板式轨道在墩台位移作用下梁轨相互作用规律研究

刘 成1，李 帅1，谢铠泽1，田春香2，王 平1

(1.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；2.中铁二院工程集团有限责任公司，成都 610031)

针对简支梁和连续梁，建立整桥系统的计算模型，对墩台位移引起的作用力作用下桥上纵连板式无砟轨道的梁轨耦合作用规律进行分析研究。研究表明：墩台位移引起的作用力是纵连式无砟轨道梁轨相互作用较重要的附加作用力，建议受日照及风荷载影响较大的高墩桥设计中考虑墩台位移引起的作用力的影响；连续梁与简支梁桥墩向右位移时所受的外荷载大致相当，轨道及桥梁各部件所受附加力也大致相等，且桥墩纵向位移越大，各部件所受附加力越大；考虑桥梁伸缩及桥墩位移的共同作用时，轨道及桥梁各部件的受力与变形均较单因素作用时量值大，且连续梁上各部件的受力与变形较简支梁大；从梁体位移方向的比较来看，当桥墩位移与桥梁伸缩方向相同时，钢轨、轨道板、端刺的受力及轨道各部件的位移较大，而当桥墩位移与桥梁伸缩方向相反时，剪力齿槽、墩台、底座板所受纵向力较大；从荷载耦合方式来看，桥梁伸缩及桥墩位移两种荷载耦合时，轨道及桥梁各部件的受力与变形要小于两种荷载单独作用后将计算结果叠加的情况，主要是由于滑动层摩阻力等线路约束阻力的塑性极限造成的。

纵连板式无砟轨道；无缝线路；墩台位移；梁轨相互作用

桥梁地段CRTSⅡ型板式无砟轨道是一种新型无砟轨道结构，它不仅改变了无砟轨道的设计理念，同时也对桥上无缝线路设计产生了深远的影响。由于底座与梁面设置有滑动层，它彻底改变了传统的梁轨相互作用的传递方式[1-2]。从理论上讲，如果滑动层处于理想状态，由于其摩擦系数很小，可以减弱温度变化和列车荷载所引起的梁轨相互作用力，从而减少轨道和桥梁承受的纵向附加力；同时在固定支座上方设置了剪力齿槽，可将列车制动力直接传递至桥梁墩台上；台后路基上设置了摩擦板、端刺等结构，可起到纵向约束连续底座板的作用；形成了钢轨在桥梁和路基上纵向连续、轨道板在桥梁及路基上纵向连续、底座板在两端刺间连续、桥梁也可纵向连续的多层连续结构，钢轨与桥梁间的相互作用较弱，能适应更大温度跨度的桥梁，有利于取消钢轨伸缩调节器及小阻力扣件的铺设，是一种新型无砟轨道结构，因此其梁轨相互作用机理及规律明显不同于有砟轨道及单元式无砟轨道桥上无缝线路。

特殊地段铺设无缝线路，需要考虑特殊荷载的作用。目前，国内学者对于高墩大跨桥上特殊荷载作用下的梁轨相互作用进行了相关研究[3-7]。刘婷林等研究温度梯度对高墩大跨桥上无缝线路的影响，针对高墩大跨桥梁桥墩受到纵向和横向温度梯度荷载时，钢轨的纵向力和梁轨相对位移进行了分析[1]；罗华鹏等研究了高墩大跨桥梁桥墩整体升温对无砟轨道中轨道部件受力和变形的影响[2]；胡志鹏等针对高墩大跨桥梁桥墩工后沉降对桥上无缝线路的影响，以某高墩大跨桥梁为例，通过有限元方法，建立线-桥-墩一体化模型，分析桥墩不均匀沉降和均匀沉降对钢轨纵向力、线路高低不平顺以及墩台受力的影响[3]等。

然而，国内外针对纵连式无砟轨道的特殊荷载作用下的梁轨相互作用规律研究较少。山区修建的高速铁路，当桥梁跨越河流、峡谷时可能会出现受日照、侧风影响较大的高墩，此时纵连式无砟轨道在桥墩自身的纵向位移作用下也会产生附加的纵向墩移力。基于此，本文建立纵连式无砟轨道全桥系统桥上无缝线路计算模型，针对桥上纵连板式无砟轨道在墩移力作用下梁轨相互作用规律进行相关研究，以期为桥上纵连板式无砟轨道无缝线路的设计、施工及后期养护维修提供参考。

1 梁轨作用机理与计算假定

1.1 梁轨作用机理

墩移力荷载作用会引起纵连板式无砟轨道系统的伸缩变形，由于剪力齿槽的固结作用，带动底座板、轨道板及钢轨的纵向位移，底座板伸缩时通过CA砂浆的粘结力和摩擦力传递给轨道板，轨道板伸缩时通过扣件纵向阻力传递给钢轨，因钢轨、道床板、底座板均为纵连结构，因此墩移力会引起钢轨伸缩力、轨道板伸缩力、底座板伸缩力[8-9]。

1.2 计算假定

纵连板式无砟轨道桥上无缝线路因轨道结构与有砟轨道、单元式无砟轨道有明显的不同，因而其梁轨相互作用机理也有所差别，计算中需采用以下假定。

(1)根据CRTSⅡ型板的结构特点，将轨道板简化为0.65 m的宽枕进行计算。

(2)假定开裂后不考虑底座混凝土板的抗弯能力，将其视为轴向拉压杆件进行计算。考虑不同工况下的刚度值按不同折减进行伸缩力计算。

(3)假设各桥墩高度相差不大，桥墩的位移量一致。

2 计算模型及参数

建立纵连式无砟轨道全桥系统桥上无缝线路计算模型如图1所示。在该模型中考虑钢轨、轨道板、底座板、摩擦板、桥梁、墩台、端刺、扣件系统、乳化沥青砂浆层、两布一膜滑动层、两布摩擦层等部件的纵向作用，分别采用梁单元、杆单元或弹簧单元来模拟，底座板侧向挡块主要约束轨道板和底座板的横向位移、底座板的竖向位移，而允许轨道板、底座板的纵向伸缩，因而可不考虑该部件的影响。沿线路横向，考虑到铺设纵连板式无砟轨道的高速铁路桥梁大多数为整体箱梁，单根钢轨折断时，其他钢轨对桥梁的纵向约束较大；单线轨道板或底座板折断时，邻线会约束桥梁的纵向位移；当单侧线路出现较多病害，如轨道板与底座板离缝，而另一侧线路状态良好时，以及在不同地段交替出现、同时出现时，需考虑两线路间的相互作用。因此在计算技术的发展使得“一桥一算”不再困难时等情况下，建立多根钢轨、整体桥梁结构的系统模型。

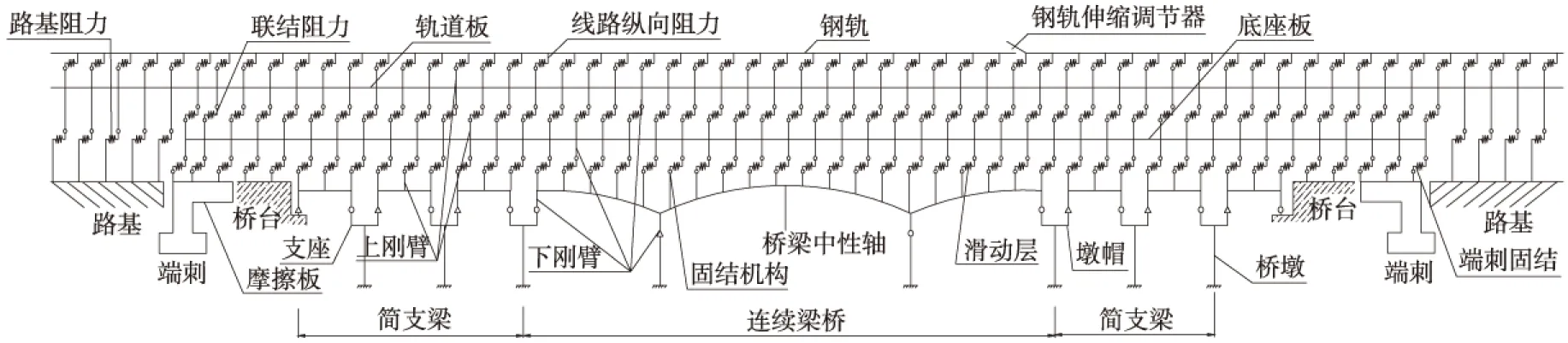
图1 整桥计算模型

计算采用简支梁、连续梁两种桥梁形式进行计算分析，简支梁桥型：5跨32 m简支梁；连续梁桥型：2×32 m简支梁+(32+48+32) m连续梁+2×32 m简支梁。为安全计，考虑最不利工况下的梁轨作用规律以及墩台受力极值，升温情况下轨道板与钢轨为40 ℃、底座板与桥梁为30 ℃，升温情况下轨道板与底座板伸缩刚度不折减，降温情况下轨道板与底座板伸缩刚度折减系数为0.1[6-9]。线路纵向阻力、墩台刚度等取值参考《铁路无缝线路设计规范》(TB10015—2012)。

参考相关文献中设计和试验研究[10-15]，本文 “两布一膜”滑动层摩擦系数取为0.35、“两布”隔离层摩擦系数按0.70取值，路基上“两布”隔离层滑动前最大相对位移为5.0 mm，桥梁上“两布一膜”隔离层滑动前最大相对位移为5.0 mm；计算中CA砂浆取层间粘结阻力为63.8 kN/m，极限位移为0.5 mm；摩擦板长度取为45.5 m。采用Π形端刺，纵向水平刚度为1.0×107kN/m，根据A、B组填料的的线弹性范围确定端刺纵向位移限值为3.0 mm；模型中8根联结销钉的纵向水平刚度按德国设计建议取值为4.0×104kN/m。

3 墩移力的分布规律

以升温为例，假设除桥台外，各桥墩的纵向位移为5 mm[16-18]，不考虑桥梁的伸缩位移，简支梁及连续梁上钢轨纵向附加力分布如图2所示，桥梁及轨道各部件的位移分布如图3所示。

图2 钢轨墩移力

从图2、图3可见，桥墩向右位移带动梁体整体向右位移，同伸缩附加力的产生机理一样，钢轨在右桥台附近出现最大附加压力，左桥台附近出现最大附加拉力；由于简支梁及连续梁桥墩纵向位移均设为5 mm，两种梁型上钢轨最大附加压力均约为77.5 kN；由于剪力齿槽的固结作用，带动底座板、轨道板及钢轨的最大纵向位移均较大，致使钢轨墩移力还远大于伸缩力；钢轨与轨道板、轨道板与底座板、底座板与梁体间的最大相对位移均在0.1 mm左右。由此可知，墩移力是纵连式无砟轨道梁轨相互作用所引起的较重要的附加作用力；受日照及风荷载影响较大的高墩桥，在选用纵连式无砟轨道结构时，在设计中应考虑这种墩移力的影响。

简支梁与连续梁上轨道板及底座板的纵向力分布如图4所示，剪力齿槽及桥墩受力如图5所示。

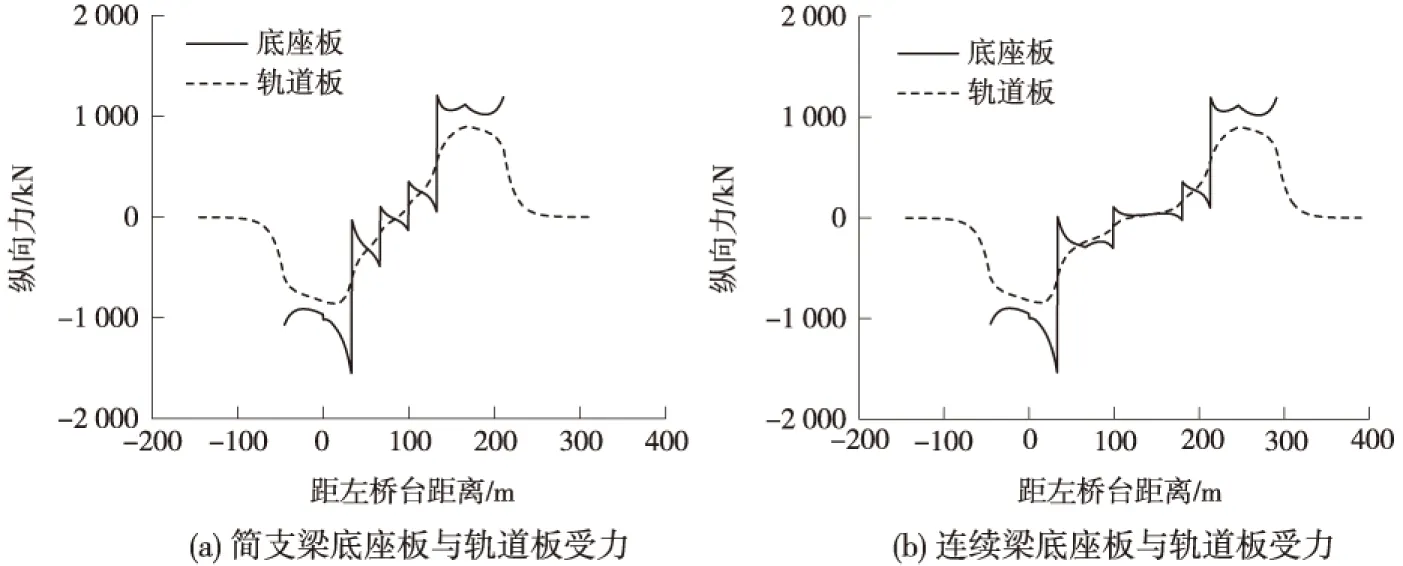
图4 底座板与轨道板受力

图5 剪力齿槽与桥墩受力

从图4、图5可见，由于剪力齿槽在带动底座板跟随固定支座上方梁体位移的过程中受力较大，如连续梁上剪力齿槽所受最大纵向力约为1 569.1 kN，因而传递至底座板上的纵向力也较大，致使轨道板及底座板所受墩移附加力均较大；左桥台起着锚固作用，梁体向右移动过程中所产生的纵向力需要左桥台及连续轨道结构来共同承受，因而左桥台所受纵向力也较大；因算例中连续梁与简支梁桥墩向右位移时所受的外荷载大致相当(即各固定支座桥墩产生5 mm位移时所受纵向荷载之和)，因而轨道及桥梁各部件所受墩移附加力也大致相等。很显然，桥墩纵向位移越大，各部件所受墩移力越大；各桥墩高度、纵向水平刚度、左右侧温度差等影响因素不同，各桥墩纵向位移也不会相同，设计检算中需要采用各桥墩的实际纵向位移来计算。

4 墩移力与伸缩力耦合分析

前面计算墩移力时未考虑桥梁的伸缩位移，其计算结果与伸缩力叠加后如表1所示，表中还列出了墩移力与伸缩力同向耦合(桥墩位移方向与桥梁伸缩方向相同)、墩移力与伸缩力反向耦合(桥墩位移方向与桥梁伸缩方向相反)时的计算结果。

从表1可见，考虑桥梁伸缩及桥墩位移的共同作用时，轨道及桥梁各部件的受力与变形均较单因素作用时量值大，且连续梁上各部件的受力与变形较简支梁大；从梁体位移方向的比较来看，当桥墩位移与桥梁伸缩方向相同时，钢轨、轨道板、端刺的受力及轨道各部件的位移要大一些，而当桥墩位移与桥梁伸缩方向相反时，剪力齿槽、墩台、底座板所受纵向力要大一些，因而在设计中需要根据不同的检算对象，选取最不利的位移组合；从荷载耦合方式来看，桥梁伸缩及桥墩位移两种荷载耦合在一起计算时，轨道及桥梁各部件的受力与变形要小于两种荷载单独作用后将计算结果叠加的情况，这主要是由于滑动层摩阻力等线路约束阻力的塑性极限造成的。若要用墩移力代替伸缩力进行检算，则应将两种荷载耦合在一起计算。

表1 墩移力与伸缩力耦合计算结果

5 结论及建议

通过建立纵连板式无砟轨道整体系统模型，墩移力对简支梁和连续梁桥上纵连板无砟轨道无缝线路作用进行分析，得到以下几点结论。

(1)墩移力是纵连式无砟轨道梁轨相互作用所引起的较重要的附加作用力。建议受日照及风荷载影响较大的高墩桥，在选用纵连式无砟轨道结构时，在设计中应考虑墩移力的影响。

(2)连续梁与简支梁桥墩向右位移时所受的外荷载大致相当，因而轨道及桥梁各部件所受墩移附加力也大致相等。很显然，桥墩纵向位移越大，各部件所受墩移力越大。建议检算中需要根据实际各桥墩高度、纵向水平刚度、左右侧温度差等设计条件，采用各桥墩的实际纵向位移来计算。

(3)考虑桥梁伸缩及桥墩位移的共同作用时，轨道及桥梁各部件的受力与变形均较单因素作用时量值大，且连续梁上各部件的受力与变形较简支梁大。

(4)从梁体位移方向的比较来看，当桥墩位移与桥梁伸缩方向相同时，钢轨、轨道板、端刺的受力及轨道各部件的位移较大，而当桥墩位移与桥梁伸缩方向相反时，剪力齿槽、墩台、底座板所受纵向力较大，因而在设计中需要根据不同的检算对象，选取最不利的位移组合。

(5)从荷载耦合方式来看，桥梁伸缩及桥墩位移两种荷载耦合在一起计算时，轨道及桥梁各部件的受力与变形要小于两种荷载单独作用后将计算结果叠加的情况，这主要是由于滑动层摩阻力等线路约束阻力的塑性极限造成的。若用墩移力代替伸缩力进行检算，则应将两种荷载耦合计算。

[1] 蔡小培，高亮，孙汉武，等.桥上纵连板式无砟轨道无缝线路力学性能分析[J].中国铁道科学，2011，32(6):28-33.

[2] 徐锡江，魏建兵.大跨连续刚构桥上CRTSⅡ型板式轨道纵向力分析[J].高速铁路技术，2012，3(4):52-56.

[3] 刘婷林，代先星，肖杰灵，等.温度梯度对高墩桥上无缝线路的影响分析[J].铁道建筑，2014(4):121-124.

[4] 罗华朋，马旭峰，肖杰灵，等.桥墩温度荷载对高墩大跨桥上无砟轨道无缝线路的影响研究[J].铁道建筑，2015(6):127-130.

[5] 胡志鹏，谢铠泽，朱浩，等.高墩大跨桥梁桥墩沉降对桥上无缝线路的影响[J].铁道标准设计，2013，57(10):23-26.

[6] 段翔远，徐井芒，陈嵘.静风荷载对高墩大跨桥梁位移影响分析[J].铁道建筑，2011(9):1-4.

[7] 罗华朋，邢俊，杨凯，等.桥墩温度梯度对高墩大跨桥上无砟轨道影响研究[J].铁道标准设计，2015，59(8):26-29.

[8] 闫斌，刘从新，杜凯，等.门式墩上高速铁路连续梁桥梁轨相互作用[J].华中科技大学学报(自然科学版)，2012，40(3) ：81-84.

[9] 闫斌，戴公连，董林育.客运专线斜拉桥梁轨相互作用设计参数[J].交通运输工程学报，2012，12(1) ：31-37.

[10]张亚爽.简支梁长桥上CRTSⅡ型板式无砟轨道底座板施工受力分析[D].成都:西南交通大学，2014.

[11]Bogl S. Slab Track System-FF Bogl[J]. Railway Technical Review，2006(S):32-35.

[12]高亮.高速铁路无缝线路关键技术研究与应用[M].北京:中国铁道出版社，2012.

[13]刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法[M].成都:西南交通大学出版社，2010.

[14]DIN1045-1.2001 Concrete， reinforced and prestressed concrete structures-Part1： Design and construction[S]. Beuth Verlag， Berlin， 2001.

[15]Liu F S，Zeng Z P，Wu B et al. Study of the Effect of Cement Asphalt Mortar Disease on Mechanical Properties of CRTSII Slab Ballastless Track[J]. Advanced Materials Research， 2014，906:305-310.

[16]段翔远，荆果，徐井芒，等.高墩大跨桥梁变形对无砟轨道的影响[J].铁道建筑，2011(8):1-4.

[17]刘浩，朱浩，王平，等.风荷载对高墩大跨桥梁桥上无缝线路的影响[J].铁道建筑，2013(12):15-18.

[18]段翔远，徐井芒，陈嵘.静风荷载对高墩大跨桥梁位移影响分析[J].铁道建筑，2011(9):1-4.

Beam and Track Interaction of Continuous-slab-track Subject to Pier Displacement

LIU Cheng1， LI Shuai1， XIE Kai-ze1， TIAN Chun-xiang2， WANG Ping1

(1.Key Laboratory of High-Speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031， China;2.The Second Survey and Design Institute of China Railway; Chengdu 610031， China)

In this paper， for the simply supported bridge and continuous bridge， the calculation model of integral bridges is established to analyze the rules of bridge-track interaction subject to the force caused by pier displacement. The results show that the force caused by pier displacement is a significant additional force between bridge and track. Thus， it is recommended that the force caused by pier displacement should be considered in the design of high-pier bridge due to great impact of sunshine and wind load. The continuous beams and simply supported beams are subjected to much the same force when their piers are shifted rightward， and various components of tracks and bridges suffer roughly equal additional forces， and larger the longitudinal displacement of piers， greater the force each additional member suffers. In case of simultaneous bridge stretching and pier shifting， the force and deformation of each member of the track and bridge are larger than those when only single factor is considered， and the force and deformation of continuous beams are larger than those of the simply supported beams. in comparison of beam displacement direction， when the displacement of bridge stretching the and pier moving are in the same direction， the force of rails， track plate， barbed end are relatively larger and the deformation of various components of tracks are relatively larger; when the bridges stretching and piers moving in the opposite direction， the shear gullet， the pier， and the base plate bear bigger longitudinal force. With respect to the point of loads coupling， when the coupling of bridges stretching and piers moving is considered， the force and displacement of track and bridge component are smaller than those when two loads are separated with the calculation of the results superposed， which is mainly due to the fact that the friction resistance of sliding layer and other tract restraining forces reach the plastic limits．

Continuous-slab-track; CWR; Pier displacement; Bridge and rail interaction

2016-04-14；

2016-05-21

国家自然科学基金委“高速铁路基础研究联合基金”重点支持项目(U1334203&U1234201)

刘 成( 1992—)，男，硕士研究生，E-mail:1351075626@qq.com。

1004-2954(2016)12-0008-05

U441+.7

A

10.13238/j.issn.1004-2954.2016.12.003