基于自适应形态滤波和FSWT的轨道表面凹陷长度检测

蒋 杰，高旭东，王夫歌，邢宗义

(1.南京理工大学机械工程学院，南京 210094；2.南京理工大学自动化学院，南京 210094)



基于自适应形态滤波和FSWT的轨道表面凹陷长度检测

蒋 杰1，高旭东1，王夫歌1，邢宗义2

(1.南京理工大学机械工程学院，南京 210094；2.南京理工大学自动化学院，南京 210094)

为了对轨道表面凹陷长度进行检测，提出一种基于自适应形态滤波(Adaptive Morphological Filtering，AMF)和频率切片小波变换(Frequency Slice Wavelet Transform，FSWT)的轨道表面凹陷长度检测方法。首先，建立轮轨动力学模型，研究轴箱加速度频率与轨道不平顺频率之间的关系；其次，研究AMF和FSWT的基本原理，并对FSWT中切片函数进行改进，提高FSWT对不同信号的适应性；最后，对某地铁列车的轴箱实测信号进行分析，估算轨道表面凹陷长度。结果表明该方法具有工程可行性。

轨道不平顺；轨道凹陷；轴箱加速度；自适应形态滤波；FSWT

1 概述

列车运营过程中，轨道存在不平顺情况是引起列车异常振动的首要原因。轨道凹陷作为轨道短波不平顺的一种，将引起列车振动加剧，降低列车零部件寿命，严重情况下将使轨道磨损，危及行车安全[1]。

轨道交通行业专家对轨道状况检测进行了大量的研究。Molina L F等[2]在运营车辆上加装机器视觉仪器对轨道状况进行检测；Lee J S[3]通过对轴箱振动信号依次进行Kalman空间滤波、带通滤波和RLS自适应滤波，实现轨道垂向不平顺的在线监测；J.I.Real[4]采用二次积分、高通滤波和相位补偿等技术剔除车轮踏面故障、噪声干扰等无效信号，实现轨道垂向不平顺的监测。魏云鹏[5]利用ANSYS建立了轮轨接触的有限元模型，分析了轮轨系统在轨道不平顺功率谱激励下的动力响应。潘海泽等[6]提出灰色预测模型和灰色-马尔可夫预测模型分别对TQI(轨道质量指数)进行预测，并基于实测数据进行了理论验证。丁建明等[7]采用现代频率切片小波变换对轨道表面凹陷引起的前后轮振动特性进行时频特征分析，进而判断轨道局部是否存在缺陷，并采用动力学仿真模型进行验证。张重王等[8]建立了列车-无砟轨道-路基系统垂向耦合动力模型，计算分析3种不平顺谱下车辆和轨道系统的动力响应，得出了不同轨道谱作用下车辆与轨道系统动力响应具有较大的差异的结论。

以上对轨道状况的检测研究均停留在定性层面，并未对轨道凹陷的特征参数进行检测研究。本文在国内外研究基础上，提出基于AMF和FSWT的轨道表面凹陷长度检测方法，通过对信号进行滤波和频率切片小波变换分析，获得细化频谱图中幅值最大时对应的故障特征频率，并根据列车速度和故障特征频率，估算轨道表面凹陷长度。

2 轮轨动力学模型

轮轨动力学模型是分析轨道不平顺对轮对受力和振动影响的常用工具，包括列车和轨道两个部分，在实际分析时常常将两部分进行简化，分别考虑轮轨间的高频冲击和车辆簧上部分的振动[9]，建立如图1所示的列车集总参数简化模型。其中，K1表示轮轨之间的弹性接触刚度，m1为簧下质量，m2为轨道的换算质量，K2为轨道垂向刚度，c2为轨道垂向阻尼，z1和z2分别表示簧下质量与轨道相对于静平衡位置的位移，取向下方向为正。

图1 列车集总参数简化模型

当列车运行速度为V，轮轨的垂向动力学方程可表示为

当轨道存在不平顺η后，轨道相对于静平衡位置的位移可表示为z2+η，则式(1)转化为

对式(2)进行常系数微分方程的求解，可得

式中，Ai、pi、B为常数，其值大小由ω1、ω2、K1、K2等参数共同决定。

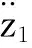
3 轨道凹陷长度检测原理

轨道表面凹陷长度检测主要包括自适应形态滤波和频率切片小波变换两部分，下面进行原理介绍。

3.1 自适应形态滤波器

首先介绍本形态学变换，然后根据所要分析信号的特点，选取不同的结构元素，最后根据不同的结构元素构建最优的滤波器。

3.1.1 基本形态学变换

数学形态学的基本运算包括腐蚀、膨胀、形态开和形态闭运算。其中，腐蚀和膨胀是数学形态学中两个最基本的变换。

设输入序列f(n)和结构元素g(n)分别为定义在F={0，1，…，N-1}和G={0，1，…，M-1}上的一维离散函数，且N≥M，则

f(n)关于g(n)的腐蚀变换为

f(n)关于g(n)的膨胀变换为

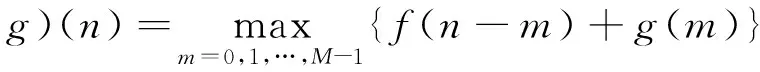
f(n)关于g(n)的开变换为

(f∘g)(n)=(fΘg⊕

f(n)关于g(n)的闭变换为

(f·g)(n)=(f⊕

形态开可以平滑信号中的正冲击，形态闭可以平滑信号中的负冲击。

3.1.2 自适应形态滤波

传统的形态滤波器大多采用单一结构元素对信号进行形态学滤波处理，这种方法虽然简单易行，但滤波效果依赖于结构元素的选择，要想得到较好的滤波效果，必须对待分析信号有充分的预先了解，但是实际情况是，工程信号往往较为复杂，往往包含多种噪声类型，难以根据先验知识选择合适的结构元素。因而，针对不同的噪声类型有必要选择不同的结构元素并进行相应的组合[10]。

如果选取不同尺度的结构元素进行组合，将构成广义形态滤波器

式中，FGoc(f(n))=(f∘g1·g2)(n)

FGco(f(n))=(f·g1∘g2)(n)

其中，g1(n)和g2(n)分别为不同的结构元素。

本文采用特征频率强度系数量化各结构元素对列车轴箱垂向振动信号的处理能力，特征频率强度系数越大，特征频率越明显，与之相应的模式出现的概率就越高。特征频率强度系数表达式如式(9)所示，其定义为频谱中特征频率各倍频幅值与频率幅值总和的比值。

式中，FCi(i=1，2，3)为频谱中特征频率各倍频幅值；Fj(j=1，2，…，N-1)为频率幅值。

在不同尺度结构元素作用下，特征频率强度系数具有不同的幅值大小，按照幅值大小进行排序选择最优的结构元素，进而按照式(8)组合最优滤波器[11]。

3.2 频率切片小波变换及其改进

Yan Z[12]等在充分吸收短时傅里叶变换和小波变换的优点基础之上，引入频率切片函数，提出了一种新的时频分析方法-频率切片小波变换(Frequency Slice Wavelet Transform，FSWT)。

对于任意信号f(t)∈L2(R)，其频率切片小波变换定义如下[13]

从而，频率切片函数改进为

式中，x，a，b为大于0的常量。

FSWT很好地解决了传统小波重构信号必须依赖于小波基，其逆变换与切片函数也没有直接关联，所以可采用快速傅里叶变换对分离信号进行重构，而无需像小波变换严格遵守容许性条件。

在信号的时频变换区间内，目标区间可通过选择时频切片区间(t1，t2，ω1，ω2)进行分离重构：

4 实验分析

以某地铁公司A型车实测的轴箱垂向振动信号为例，对其分别进行自适应形态滤波预处理和频率切片小波变换，以验证所提方法的工程适应性。该A型车轴箱垂向振动加速度传感器采样频率为20 kHz，列车运行速度为10 m/s。

图2为采样时间1 s内轴箱垂向振动信号的波形图，可以看出，实测轴箱垂向振动信号在0.190、0.922和0.720 s受噪声干扰较大，振动信号在0.6 s和0.7 s处存在明显的振动冲击且0.7 s处的振动冲击相对复杂。为进一步取得信号故障特征信息，需对振动信号进行滤波，降低干扰信号对分析结果的影响。

图2 地铁轴箱实测振动信号

根据自适应形态滤波器构造原理，首先计算实测振动信号结构元素参数，结构元素的长度尺度序列L为[6，20]，结构元素高度尺度H为[0，0.682 6]，对实测轴箱垂向振动信号进行形态开运算、形态闭运算、形态开闭运算、形态闭开运算，在不同形态运算下最优结构元素如表1所示，图3为在不同算子及结构元素下的频率强度系数图。

图3 在不同算子及结构元素下的频率强度系数

表1 最优结构元素的选取

从图3可以看出，形态开闭运算和形态闭开运算的频率强度系数在[0.05 0.12]之间波动，而形态开和形态闭运算的频率强度系数最大不超过0.04，表明形态开闭运算和形态闭开运算滤波效果较好。由于单独的形态开-闭滤波器会增加强负冲击噪声，形态闭-开滤波器不能完全滤除正冲击噪声，本文选用长度为16的上三角结构元素和长度为11的下半圆结构元素构成广义形态滤波器对原始信号进行处理。

图4为滤波后轴箱实测振动信号，从图中可以看出，经过自适应形态滤波后轴箱垂向振动信号更加平滑，0.190 s和0.922 s附近可能存在异常振动被有效剔除，振动冲击时间点相对更加清晰，即使在0.7 s附近也可以清晰区分出振动异常时间点，优于巴特沃斯滤波器达到的滤波效果。

图4 滤波后轴箱实测振动信号

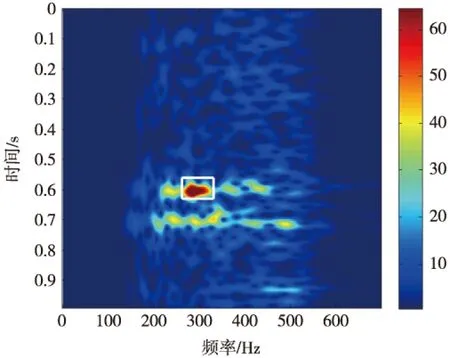
图5 轴箱实测振动信号时频图

图6 轴箱实测振动信号时频图

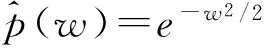
图6中时频幅值最大的两个目标区域分别为[0.56s，0.63s，262Hz，332Hz]和[0.65s，0.72s，313Hz，369Hz]，根据公式(12)分离目标区域a和b。图7为目标区域的重构信号，可以看出经过频率切片小波变换后，信号重构效果良好，比原始信号更加平滑，振动冲击更加清晰。

图8和图9分别为目标区域a和目标区域b的细化频谱。目标区域a的幅值峰值对应频率为281Hz，目标区域b的幅值峰值对应频率为338.5Hz，因此可以判断轨道对列车存在1个281Hz和338.5Hz的冲击信号，在10m/s的列车运行速度条件下，由公式可计算出轨道表面凹陷长度分别为35.4mm和29.5mm，两者均属于中等轨道表面凹陷，这与现场实际的轨道凹陷情况基本吻合，说明该方法具有工程可行性。

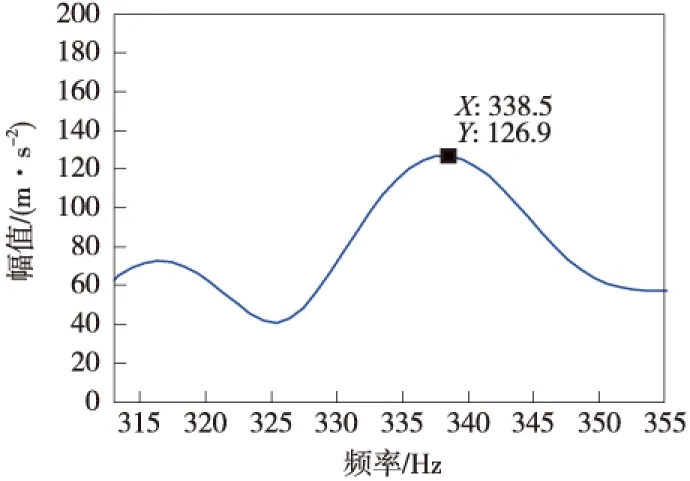
图9 目标区域b的细化频谱和时频幅值

5 结语

本文研究了一种基于自适应形态滤波和频率切片小波变换的轨道表面凹陷长度检测方法，首先根据轴箱实测数据，构建自适应形态组合滤波器，消除噪声等干扰信号的影响，然后将改进后的频率切片小波变换应用于轴箱垂向振动信号分析，对选定的目标区域进一步细化分析，获得更加精确的故障特征信息，最后，利用所推导的数学关系求出轨道凹陷长度，通过和现场实际对比，验证了所提方法的准确性和工程可行性。

[1] 高建敏，翟婉明.高速铁路钢轨焊接区不平顺的动力效应及其安全限值研究[J].中国科学：技术科学，2014，44(7):697-706.

[2]MolinaLF，ResendizE，EdwardsJR，etal.Conditionmonitoringofrailwayturnoutsandothertrackcomponentsusingmachinevision[C]∥TransportationResearchBoard90thAnnualMeeting， 2011.

[3]LeeJS，ChoiS，KimSS，etal.Amixedfilteringapproachfortrackconditionmonitoringusingaccelerometersontheaxleboxandbogie[J].IEEETransactionsonInstrumentation&Measurement， 2012，61(3):749-758.

[4]RealJI，MontalbnL，RealT，etal.Developmentofasystemtoobtainverticaltrackgeometrymeasuringaxle-boxaccelerationsfromin-servicetrains[J].JournalofVibroengineering， 2012，14(2)：813-826.

[5] 魏云鹏，吴亚平，陈鄂，等.基于ANSYS轨道不平顺条件下轮轨系统频谱动力响应分析[J].铁道标准设计，2015，59(5):51-54.

[6] 潘海泽，黄远春，汪磊，等.基于灰色GM(1，1)和灰色-马尔可夫模型的轨道几何不平顺预测及应用研究[J].铁道标准设计，2010(10):5-9.

[7] 丁建明，林建辉，王晗，等.轨道局部缺陷动态检测冲击特征定位比较法[J].振动与冲击，2014，33(6):113-117.

[8] 张重王，刘学毅，苏成光，等.不平顺谱对列车轨道系统动力性能影响的对比分析[J].铁道标准设计，2015，59(7):15-19.

[9] 张健，金学松，肖新标，等.车辆-轨道耦合动力学钢轨模型求解方法[J].交通运输工程学报，2011，11(2):32-38.

[10]崔宝珍.自适应形态滤波与局域波分解理论及滚动轴承故障诊断[D].太原：中北大学，2013.

[11]李兵，张培林，刘东升，等.基于自适应多尺度形态梯度变换的滚动轴承故障特征提取[J].振动与冲击，2011，30(10):104-108.

[12]YanZ，MiyamotoA，JiangZ，etal.Anoveralltheoreticaldescriptionoffrequencyslicewavelettransform[J].MechanicalSystemsandSignalProcessing， 2010，24(2):491-507.

[13]段晨东，高强.基于频率切片小波变换的结构健康状态分析[C]∥第十二届全国设备故障诊断学术会议论文集，2010.

[14]张宇辉，刘梦婕，黄南天，等.频率切片小波变换在局部放电信号分析中的应用[J].高电压技术，2015，41(7):2283-2293.

[15]BiswalB，MishraS.Powersignaldisturbanceidentificationandclassificationusingamodifiedfrequencyslicewavelettransform[J].Generation，Transmission&Distribution，IET， 2014，8(2):353-362.

Detection of Track Surface Squat Length Based on AMF and FSWT

JIANG Jie1， GAO Xu-dong1， WANG Fu-ge1， XING Zong-yi2

(1.College of Mechanical Engineering， Nanjing University of Science and Technology， Nanjing 210094， China2.College of Automation， Nanjing University of Science and Technology， Nanjing 210094， China)

A method based on Adaptive Morphological Filtering (AMF) and Frequency Slice Wavelet Transform (FSWT) is proposed to detect the length of track surface squats. Firstly， the dynamic model of wheel/rail is established to identify the relation between the frequency of axle box acceleration and that of track irregularity. Secondly， the basic principles of AMF and FSWT are introduced， and the slice function in FSWT is improved to advance the adaptability of FSWT to different signals. Finally， the measured axle box signals from a subway train are analyzed to estimate the length of squats. The results show that the method is of engineering feasibility.

Track irregularity; Track squats; Axle box acceleration; AMF; FSWT

2016-04-14；

2016-05-23

国家重点研发计划项目(2016YFB1200402)

蒋 杰(1992—)，男，硕士研究生，主要从事轨道交通控制与安全研究，E-mail:15005158965@163.com。

1004-2954(2016)12-0017-05

U213.4+3

A

10.13238/j.issn.1004-2954.2016.12.005