光学方法在真空计量中应用研究进展

习振华，李得天，成永军，孙雯君，张虎忠，袁征难，吉 康

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

光学方法在真空计量中应用研究进展

习振华，李得天，成永军，孙雯君，张虎忠，袁征难，吉 康

（兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000）

光学方法在真空计量中的应用研究是真空计量中的新学科。固定长度法布里-珀罗光学谐振腔应用在粗低真空校准技术、可调谐二极管激光吸收光谱（TDLAS）应用在分压力校准技术、迈克尔逊干涉仪动态真空校准技术以及基于法布里-珀罗（Fabry-Pérot）光学干涉法应用在气体微流量测量技术。文中介绍了原理、校准装置的结构及性能等。从中可以看出，近年来随着学科的交叉融合，采用光学方法的真空计量技术大幅减小了现有真空计量标准的测量不确定度，促进真空计量由实物标准向量子标准转变，并对真空基本量复现，以及今后真空国际单位制的重新定义具有重要的意义。

真空标准；激光干涉；激光吸收光谱；动态真空；气体微流量

0 引言

随着诸多计量参数对应的实物标准向量子标准转变，国际计量发展面临着重大的挑战，由此将引发国际计量体系历史性的变革，基于光学方法的真空计量新方法、新概念进一步发展，如激光干涉、激光吸收光谱（TDLAS）、光腔衰荡光谱（CRDS）、傅里叶变换红外光谱（FTIRS）等光学方法成为国际真空计量领域研究的热点。基于光学方法的真空计量技术对真空基本量复现和真空国际单位制的重新定义（由p的SI单位Pa向气体密度ρ（mol/m3）变化）具有深远影响，为真空计量技术发展提供了新的探索方向及研究领域。将对国际上各计量技术机构已开展的基于光学方法的真空计量标准及校准方法进行探讨研究。

1 固定长度法布里-珀罗光学谐振腔粗低真空基准

美国国家标准与技术研究院（NIST）率先提出基于法布里-珀罗（Fabry-Perot）光学干涉测量折射率反演真空度的真空标准设想。2014年已开始启动计量科学创新计划（Innovations in Measurement Science，IMS），研建新一代真空计量基准——基于光学方法的量子真空计量基准。利用基于固定长度（FLOC）（如图1所示）及更高精度的可变长度（VLOC）（如图2所示）的法布里-珀罗光学谐振腔实现腔内气体折射率的精确测量，进而获得气体密度以及真空度，校准范围1～105Pa，凭借其响应时间短（1 s）、灵敏度高（1×10-3Pa/1 kHz）、高准确度（1× 10-3Pa）、宽量程以及良好的复现性，有望取代自1643年至今作为基准的水银压力计[1-3]。

图1 固定长度法布里-珀罗光学谐振腔模型图

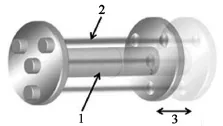
图2 可变长度法布里-珀罗光学谐振腔模型图

2015年9月在捷克布拉格举行的国际计量技术联合会第21届世界会议（21th IMEKO World Con⁃gress）上Hendricks等[2]科研人员介绍了最新进展，展示了基于固定长度（FLOC）的法布里-珀罗光学谐振腔原型，分辨力最高可达美国NIST、韩国KRISS、印度NPLI等11家国际先进国家级计量技术机构在粗低真空范围的主要基/标准——水银压力计（UIM）的35倍；最低压力点灵敏度为水银压力计下限灵敏度的10倍；精度2.0×10-4~3.5×10-5（103~105Pa）；重复性5×10-6。

气体的折射率与气体密度相关，而气体密度又由温度T及压力p决定，因此，当测得气体折射率并获得对应的温度值时，即可获得相应的真空度。该标准的光学技术基础基于法布里-珀罗光学谐振腔，如图3所示。

图3 法布里-珀罗光学谐振腔结构图

利用F-P腔测量气体折射率是一种准确度很高的测量方法[4]，测量不确定度可以达到3×10-9，测量原理由理想气体状态方程得到：

式中：T为真空室温度，K；k为玻尔茨曼常数，取1.38×10-23J/K；N为容积V中的气体分子总数；ρ为分子数密度，m-3。Lorentz-Lorenz公式揭示了折射率n和气体密度ρ之间的相互关系[5-6]，如式（2）：

式中：α为偶极子极化率；χ为抗磁磁化率。由式（2）可得：

由法布里-珀罗干涉仪中光谐振的条件得到：

由光速c=fλ和式（4）得到：

由法布里-珀罗光学谐振腔可以测得频率，此外，借助维里系数随实际气体非理想特性的修正，进而获得折射率及对应压力的测量结果，即基于法布里-珀罗光学干涉原理测量压力的理论参数模型。基于固定长度（FLOC）的法布里-珀罗光学谐振腔验证原型建立的标准如图4所示[7]。

图4 固定长度法布里-珀罗光学谐振腔粗低真空标准图

对于固定长度（FLOC）的法布里-珀罗光学谐振腔而言，结构示意图如图1（a）所示，由2个谐振腔构成，1个腔室为高真空参考端，另一腔室为测量端，每个谐振腔包含曲面反射镜、平面反射镜、封闭管路等，通过测量两束光的拍频实现气体折射率的测量。其特点在于结构简单，不包含移动部件，借助铜腔室对超低膨胀率玻璃腔室的良好包裹，温度的波动可控制在0.2 mK以下。采用电离真空计在1× 10-3~6×10-3Pa的范围内对验证原型测试灵敏度的结果如图5所示。

图5 固定长度法布里-珀罗光学谐振腔灵敏度测试图

其灵敏度达1×10-3Pa/1 kHz；其分辨力为1× 10-4Pa，是水银压力计（UIM）分辨力3.6×10-3Pa的35倍以上。采用电容薄膜真空计在0.5~2.7 Pa范围内，测试线性及响应时间的实验结果如图6所示。

其响应时间约为1 s，比UIM响应时间快1 000倍。验证原型与UIM的对比实验如图7所示，在高压力范围，两者的偏差仅为3.5×10-5。

验证原型重复性测试如图8所示，在3×104~1× 105Pa的范围内，其重复性优于5×10-6。

对于可变长度（VLOC）的法布里-珀罗光学谐振腔而言，结构示意图如图2（a）所示，由4个谐振腔构成，每个谐振腔包含曲面反射镜、平面反射镜、封闭管路及用于改变长度的移动基板（超低膨胀率玻璃）等。通过测量激光谐振频率的改变获得移动基板的位移，进而得到折射率及真空度测量结果。其特点在于固定压力点下测量折射率，可减小因压力波动导致的不确定度分量及修正角度倾斜导致的阿贝误差。

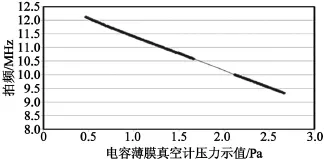
图6 固定长度法布里-珀罗光学谐振腔线性及响应时间测试

图7 固定长度法布里-珀罗光学谐振腔&UIM比对测试图

图8 固定长度法布里-珀罗光学谐振腔重复性测试图

2 可调谐二极管激光吸收光谱分压力校准装置

德国联邦物理技术研究院（PTB）作为欧洲计量研究规划（EMRP，European Metrology Research Pro⁃gramme）中IND12真空计量部分的主要参与者，将分压力校准技术及ISO国际标准的起草列为重点研究方向之一[8-9]，以解决分压力质谱计的溯源问题。目前正在实施阶段，通过对四极质谱计生产商、使用者、计量技术机构在内的24家单位问卷调查分析[10-11]，指出质谱计分压力校准技术发展的重点集中在最小可检分压力、残余气体成分分析性能等方面，并主持起草分压力校准的国际标准，如表1所列。

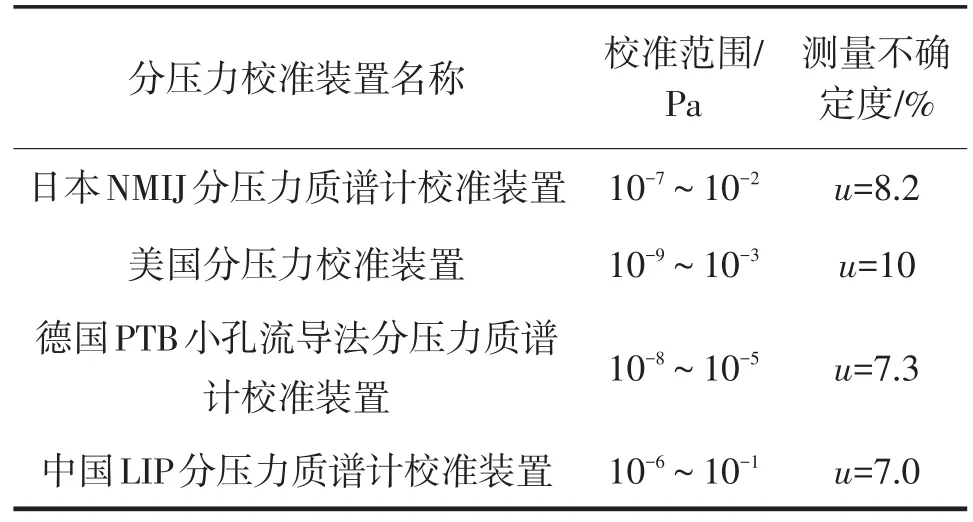
表1 国际主要计量技术机构分压力校准装置统计表

从表1可以看出，目前分压力校准技术的研究主要集中于降低分压力质谱计校准下限和减小测量不确定度两个方面，且校准多采用标样气体作为分压力校准的标准，由此产生的问题是由标样气体引入的不确定度分量较大，对于低浓度的痕量气体很难通过制备得到标样气体，限制了对极小可检分压力校准下限的延伸；此外，由于既有方法的限制，难以实现分压力校准上限向高压力范围（1~104Pa）拓展[12]。

可调谐二极管激光吸收光谱（Tunable Diode La⁃ser Absorption Spectroscopy，TDLAS）技术是光谱学遥感技术的一种，主要用来测量气体的温度和浓度。通过利用激光二极管的波长扫描和电流调谐特性对气体进行测量。由于二极管的高单色性，利用气体分子的一条孤立的吸收谱线对气体的吸收光谱进行测量，从而可方便的从混合气体中鉴别出不同的分子，避免其他光谱的干扰。该技术具有很高的灵敏度和较高的分辨率，使用指标可达ppb量级。

德国PTB建立了一套基于TDLAS技术的分压力校准装置[13-14]，如图9所示。该装置可实现CO和CO2分压力的校准，校准范围10-5～104Pa，扩展不确定度U=1.5%（k=2）；主要由激光系统、光学系统、数据处理系统以及真空系统组成。该装置除具有反应快，不确定度小的特点外，与现有分压力校准装置最主要的区别在于其高分辨率可保证在较高的压力下对较小气体分量的校准。

图9 PTB TDLAS分压力校准装置图

装置基本原理基于Beer-Lambert定律，当一束波长为λ的单色激光穿越待测气体时，气体的吸收作用会使得入射光束的强度发生变化，如图10所示，该变化可用式（6）表示：

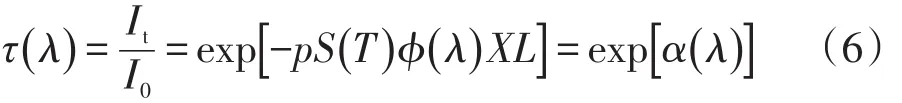
式中：τ() λ为激光透过率；I0为无气体吸收时的激光光强；It为无气体吸收时的激光光强；α(λ)为吸收率函数；X为待测气体浓度；p为气体总压力，Pa；L为激光传输距离，cm；S(T)为谱线吸收强度，cm-2atm-1； φ(λ)为线型函数。

图10 Beer-Lambert定律示意图

从式（6）可以看出，激光透过率与待测气体浓度之间存在确定的函数关系，通过一定的分析方法就可以反演出待测气体浓度，进而得到气体分压力。

TDLAS通常采用直接吸收和波长调制两种方法。其中，直接吸收法在测量中根据Beer-Lambert吸收定律，通过透射光强和入射光强的比值拟合吸收谱线，进而根据拟合得到的吸收谱线确定待测气体分压力，其物理概念清晰、操作简单，但该方法易受光强波动的影响，不适用于恶劣工况及弱吸收条件下气体分压力测量。

图11 直接吸收法示意图

装置采用具有高灵敏度的波长调制法进行测量。通过对目标信号进行高频调制，而非目标信号由于没有经过调制在后续的谐波检测过程中被除去，因此可有效的降低测量系统中背景信号的干扰，极大的提高了气体分压力的精度和灵敏度，适用于恶劣环境或弱吸收条件下的分压力测量。经高频正弦信号调制后，可得到气体分压的表达式（7）：

式中：S1f为一次谐波信号幅值；S2f为二次谐波信号幅值；L为激光传输距离，cm；S() T为谱线吸收强度，cm-2·atm-1；i1为激光器电流系数的线性强度值；H2为线函数的二次傅里叶系数。

由Lambert-Beer吸收定律可知，气体对激光的吸收作用与激光通过待测气体的有效光程成正比，有效吸收光程过短可能造成很大的测量偏差。为了提高气体分压力的测量精度和灵敏度，吸收光程的充分有效延长对装置的不确定度具有重要的影响，也是该装置的关键技术之一。White池（如图12所示）光路容易调节，可将有效吸收光程延长100倍左右，容易满足分压力校准延长光程的需求。

White池由3块镜片组成，不容易将其封装在1个真空室内进行气体分压力测量，因此该装置研制过程中，PTB采用了易于封装的Herriott池结构，并结合White池及圆形多次反射吸收池的优点，设计和加工了改进型的Herriott多次反射池（如图13所示），经多次反射后，有效光程可达100 m左右。

图12 White池结构示意图

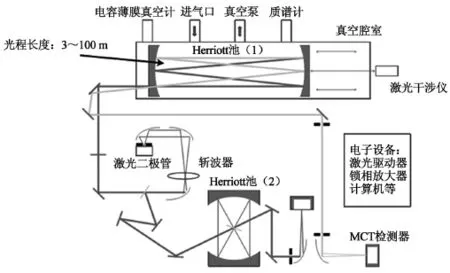
图13 Herriott多次反射池示意图

PTB采用该装置根据吸收光谱数据库HITRAN提供的R12特征吸收谱线得到CO2分压力校准结果，如图14所示，与QMS对比实验表明，在20.2~103Pa范围内其扩展不确定度仅为1.5%（k=2）。

图14 CO2分压力校准实验结果图

3 迈克尔逊干涉仪动态真空校准装置

在工业生产中，CD/DVD金属喷镀、等离子体增强化学气相沉积（PECVD）、真空镀膜等工艺中，加载互锁（Load-Lock）作为装置的重要组成部分，其真空度由大气压降至100 Pa的粗低真空范围仅需1 s甚至更短的时间（如SINGULUS公司CD金属喷镀装置105Pa至100 Pa仅需0.5 s）[9]，通过对系统真空度的实时监测，在真空计的示值达到设定的某一阈值时，实现下一工作进程的触发，因此过程控制需要真空测量响应及时，如果响应时间过长，会导致控制指令触发的相对滞后，从而造成产品质量缺陷甚至设备的损毁。目前使用的真空计通常采用实验室产生静态或动态平衡标准压力的真空标准完成校准，无法实现动态校准，“静标动用”带来的问题亟待解决[15-20]。欧洲计量研究规划（EMRP）也明确将动态真空校准研究列为工作方向之一[11]。

2014年，意大利国家计量院（INRIM）的Mari等[21]建立了1台基于迈克尔逊干涉仪的动态真空校准装置，其技术指标：（a）动态真空校准范围：1×102～1× 105Pa；（b）建立时间≤3 s；（c）相对合成标准不确定度12%。该装置利用迈克尔逊干涉仪响应时间短的特点，对动态真空标准压力进行直接测量，大幅减小了测量不确定度。

为满足高灵敏度、小体积的需要，该装置采用高灵敏度小测量臂零差迈克尔逊光学干涉仪（如图15所示）测量动态真空标准压力，快速膨胀时气体压力变化会导致相应的折射率的变化，通过真空室光路的光程也会随之发生变化。光源采用频率稳定的He-Ne（波长λ≈632.8 nm）光源，测量臂光路在上游室内经测量镜A、B多次折射后反射回来与参考臂光路相叠加，依靠高速摄影机记录干涉信号，获得正交相位信号，由计算机对其进行分析处理[22]。为提高压力的幅值和相位精度，可将叠加的干涉光路分成相差90°的两束光，一束作为X轴，另一束作为Y轴，形成Lissajous圆（如图16所示），干涉条纹移动1条时，Lissajous圆扫描1圈，使零碎条纹得到比较精确地测量。

图15 迈克尔逊光学干涉仪测量动态真空标准压力原理图

图16 Lissajous圆图及干涉图

经迈克尔逊光学干涉仪测量得到的不同压力下的光程差可得到对应的折射率，如式（8）：

式中：nj为tj时刻对应的折射率；natm为初始时刻，即上游室压力为105Pa时对应的折射率；ΔLj为t0至tj，光程差发生的改变量，m；Lopd为tj时刻对应的光程差，m。根据Lorentz-Lorenz公式，折射率与对应压力满足式（9）：

式中：n为折射率；p为气体压力，Pa；T为气体温度，K。Ai为与气体相对浓度相对应的分子极化率，根据泰勒公式及式（9）得：

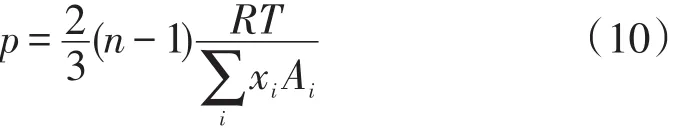
式（10）得到的压力值，即为对应时刻的快速动态真空校准的标准压力。此外，因动态真空校准采用快速膨胀的方法产生标准压力，而压力的变化会引起温度的剧烈变化，温度的快速测量及相应的温度补偿技术研究对标准压力的修正至关重要。该装置采用K型13 μm的热电偶进行数值模拟及实验验证，确定温度场分布的边界条件。

图17为采用该装置对CDG进行动态校准的结果，在3 s的动态真空校准过程中，响应时间经过优化的INFICON公司的CDG与装置生成的动态真空标准压力之间最大偏差仅为12%。

图17 INRIM动态真空校准装置CDG校准曲线图

4 法布里-珀罗光学干涉法气体微流量测量技术

瑞典国家测试和检定研究院（SNTRI）Hedlund等[23]科研人员通过法布里-珀罗（Fabry-Perot）光学干涉法测量气体密度来实现真空室内压力的精确测量，并在恒压法气体微流量计中进行了应用，实验装置如图18所示。通过测量不同单频激光的频率差，从而可以得知气体的折射率，计算的准确度可达到10-8量级。通过测量气体密度来代替传统的流量测量系统中的压力测量，避免了采用电容薄膜真空计作为前级参考压力标准，可有效减小测量不确定度。

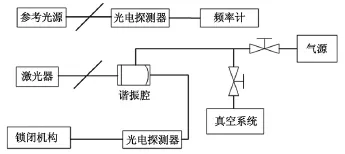
图18 基于法布里-珀罗光学干涉法的气体微流量计原理图

由于气体微流量计产生的流量Q由压力和流量计中的容积变化率决定，如式（11）：

式中：p为真空室中的压力，Pa；ΔV为Δt时间内真空室容积的变化量，m3。由理想气体状态方程得到：

式中：T为真空室温度，K；k为玻尔茨曼常数，为1.38×10-23J/K；N为容积V中的气体分子总数；ρ为分子数密度，m-3。通过式（11）、（12）及洛伦茨公式可得到流量Q的表达式：

即根据激光折射原理测量气体流量理论参数模型。

瑞典SNTRI基于法布里-珀罗光学干涉法的气体微流量计不确定度与德国PTB气体微流量计不确定度的对比如图19所示。

图19 光学干涉法气体微流量计与PTB气体微流量计的比较

实验表明，当流量为1×10-4Pa·m3/s时，PTB测量充气压力获得流量的方法其准确度为1×10-3，而采用法布里-珀罗光学干涉法测量同一压力下对应气体密度获得流量的方法其准确度为4×10-7[23-26]，比前者提高了3个量级，大幅减小了气体微流量测量的不确定度，由此将对既有的真空计量基/标准的不确定度的减小具有重要的意义。

5 结论

根据对光学方法在真空计量技术中应用的总结，可以看出，现有研究的真空校准范围主要集中在粗低真空范围（1~105Pa），可以减小现有真空计量标准的不确定度，但范围向高真空和超高真空范围延伸时，由于对应气体稀薄程度明显增加，光学方法的优势无法发挥；此外，光路系统的真空密封，适用于真空系统的小体积、高灵敏度光学系统的设计，气体折射率的温度补偿和修正，以及光学干涉仪稳频精度和拍频精度的提高等都是光学方法在真空计量技术应用中需要解决的问题。目前，正在开展此类研究，为光学方法在真空计量技术中的应用打下了良好的基础，同时也为真空计量开拓一个新的研究领域。

[1]Mozetic M，Ostrikov K，Ruzic D N，et al.Recent advances in vacuum sciences and applications[J].J Phys D：Appl phys，2014，47（15）：1-23.

[2]Hendricks J H，Stouse G，Stone J A，et al.Measurement pres⁃sure and vacuum with light：The quantum vacuum standard [C]//13thEuropeanVacuumConference，2014.

[3]HendricksJH，RickerJE，StoneJA，etal.Measurementpres⁃sureandvacuumwithlight：Anewphotonic，quantum-based，pressure standard[C]//XXI IMEKO World Congress，2015：1636-1639.

[4]Egan P，Stone J A.Absolute refractometry of dry gas to±3 parts in109[J].Appliedoptics，2011，50（19）：3076-3086.

[5]EganPF，StoneJA，HendricksJH，etal.Performanceofadu⁃al Fabty-Pérot cavity refractometer[J].Optic letters，2015，40（17）：3945-3948.

[6]Stone J A，Stejskal A.Using helium as a standard of refractive index：correcting errors in a gas refractometer[J].Metrologia，2004，41（3）：189.

[7]world’sfirstphotonicpressuresensoroutshinestraditionalmer⁃cury standard[EB/OL].www.nist.gov/pml/div685/grp01/pltims.cfm.

[8]AbouttheEMRT[EB/OL].www.emrponline.eu/.

[9]Vacuum metrology for production environments[EB/OL].www. ptb.de/emrp/vacuum.html.

[10]Jousten K.Towards calibration of quadrupole mass spectrom⁃eters：Results of questionnaire to users and manufacturers [R].PTB，2014.

[11]Final publishable JRP summary report for IND12（Vacuum）vacuum metrology for production environments[R].PTB，2015.

[12]李得天，冯焱，李正海.分压力质谱计校准装置的性能测试及校准实验[J].真空与低温，2011，7（1）：21-26.

[13]Physiker M S.Investigation of TDLAS for its Application as PrimaryStandardforPartialPressureMeasurements[D]，Ber⁃lin，2005.

[14]Lanzinger E，Jousten K.Partial pressure measurement by means of infrared laser absorption spectroscopy[J]，Vacuum，1998，51（1）：47-51.

[15]YanHuaL，HongYY，JinkuW.Developmentofvacuumme⁃trology in National Institute of Metrology[J].Vacuum，2012，86（7）：903-907.

[16]LiD，ZhaoG，GuoM，etal.Staticexpansionvacuumstandard with extended low pressure range[J].Mapan，2009，24（2）：95-100.

[17]Bergoglio M，Mari D.INRIM continuous expansion system as high vacuum primary standard for gas pressure measure⁃mentsbelow9×10-2Pa[J].Vacuum，2009，84（1）：270-273.

[18]Jousten K，Menzer H，Wandrey D，et al.New，fully automat⁃ed，primary standard for generating vacuum pressures be⁃tween 10-10Pa and 3×10-2Pa with respect to residual pres⁃sure[J].Metrologia，1999，36（6）：493-497.

[19]LiDT，GuoMR，ChengYJ，etal.Vacuum-calibrationappa⁃ratus with pressure down to 10-10Pa[J]，J Vac Sci Technol A，2010，28（5）：1099-1104.

[20]李正海.实用超高真空比对校准系统[J].真空与低温，2009，15（1）：45-47.

[21]Mari D，Bergoglio M，Pisani M，et al，Dynamic vacuum mea⁃surement by an optical interferometric technique[D]，Meas SciTechnol，2014，25（12）：125303-125310.

[22]PisaniM.AhomodyneMichelsoninterferometerwithsub-pi⁃cometer resolution[J].Measurement Science and Technolo⁃gy，2009，20（8）：084008-084014.

[23]Hedlund E，Pendrill L R.Improved determination of the gas flowrateforUHVandleakmetrologywithlaserrefractometry [J].Meas SciTechnol，2006，17（10）：2767-2772.

[24]HedlundE，PendrillLR，Addendumto‘Improveddetermina⁃tionofthegasflowrateforUHVandleakmetrologywithlaser refractometry’[J]，MeasSciTechnol，2007，18：3361-3363.

[25]Silander I，Zelan M，Axner O，et al.Optical measurement of the gas number density in a Fabry-Perot cavity[J].Meas Sci Technol，2013，24（10）：105207-10212.

[26]HedekvistPO，HenrikssonN，JonassonV.Progressreporton low flow measurements based on optical characterization of gasdensityinvacuum[R].SPTechnicalRcsearchInstituteof Sweden，2010.

RECENT ADVANCES OF VACUUM METROLOGY TECHNIQUES AND APPLICATIONS WITH OPTICAL METHODS

XI Zhen-hua，LI De-tian，CHENG Yong-jun，SUN Wen-jun，ZHANG Hu-zhong，YUAN Zheng-nan，JI Kang
（Science and Technology on Vacuum Technology and Physics Laboratory，Lanzhou Institute of Physics，Lanzhou 730000，China）

Abstrct：The research and development works with optical methods are considered to be one emerging area in the field of vacuum metrology.Typical examples of these kinds of techniques for primary and secondary standards are presented，such as the fixed-length，Fabry-Pérot optical cavity for the rough vacuum regime，Tunable Diode Laser Absorption Spectroscopy（TDLAS）for its use as a primary standard for partial pressure measurement，dynamic vacuum calibration with Michelson interferometer and determination of the gas micro-flow by the optical interferometric technique.It can be convinced that the measurement uncertainties of the current vacuum standards will be reduced substantially by the optical methods.At the same time，the future of vacuum measurement will rely on quantum-based primary standard which represents a disruptive change in the way of realizing and disseminating the SI unit of pressure，the pascal.

vacuum primary standard；laser interferometry；TDLAS；dynamic vacuum；gas micro-flow

TB771

A

1006-7086（2016）06-0311-08

10.3969/j.issn.1006-7086.2016.06.001

2016-08-21

国家自然科学基金（61501212、61471184）

习振华（1984-），男，陕西合阳人，工程师，硕士，从事真空计量研究工作。E-mail：comanche_xzh@126.com。