一道竞赛题的推广及其引发的解题教学思考

四川师范大学数学与软件科学学院(610068) 刘婷

一道竞赛题的推广及其引发的解题教学思考

四川师范大学数学与软件科学学院(610068) 刘婷

某天有幸读到一篇文章,发现马小为先生和此文作者先后对同一道竞赛填空题进行了研究.马小为先生的解答下称解法1,此文作者在该基础上改进,提出了另一种解法(下称解法2).解法2确实较巧妙、简洁,让人看后很是欣赏.

笔者对此题也较感兴趣,此题的三角形是给定的,又涉及内心,考虑到三角形不仅有锐角、钝角、直角三角形之分,而且除了内心,还有旁心、外心、垂心、重心,便觉得推广的可能性较大,但笔者翻阅过许多文献,并未发现有人对此题做过推广,因此更加好奇,便自己尝试着推广及解答.在解答时,笔者深深体会到了解法1和解法2的利弊,解法2的思路虽巧妙,但不能用于某些推论的解答:而解法1的思路却可以解答所有推论.由此,我对解法1、解法2有了不同的看法,并对解题教学进行了一番思考.

众所周知,数学与解题是紧密相连的.学习数学的主要过程就是解题,学生通过解题可以加强对数学知识、技能的理解与掌握.毫无疑问,解题教学是数学教学的一个重要部分,但现实教学中,许多老师因不注重教学方法而形成题海战术,致使学生身心疲惫,甚至厌恶数学,极不利于学生的长远发展.因此,如何提高解题教学的效率是数学教学中不可避免的问题,是每位数学教师必须思考的问题.

通过对此竞赛题进行的一系列推广及解答,我对解题教学有了一些思考,希望能与读者分享.下面展示该竞赛题的不同解法和一系列推广(其中,推广1、2、5适合初中:但推广3、4的解答因涉及余弦定理,故适合高中)以及自己对教学的思考.

一、赛题再现

如图1,△ABC中,AB=7,BC=8,CA=9,过△ABC的内切圆圆心I作DE//BC,分别与AB、AC相交于点D、E,则DE的长为____.(“《数学周报》杯”2008年全国初中数学竞赛试题)

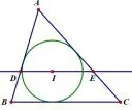
图1

二、赛题解答

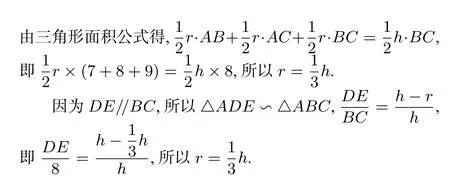
解法2:如图2,连接IB、IC,因为⊙I为△ABC的内切圆,所以∠DBI=∠IBC.因为DE//BC,所以∠DIB=∠IBC,∠DBI=∠DIB,所以DI=DB.同理IE=EC,所以DE=DI+IE=DB+EC,所以△ADE的周长为=AD+DE+AE=AD+DB+EC+AE=AB+AC=16.因为DE//BC,所以△ADE∽△ABC,所

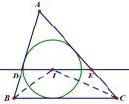
图2

三、解法分析

此题是求DE的长度,而题中已知BC的长度和DE//BC,便很容易想到通过求得△ADE与△ABC的相似比来求DE的长度,于是问题转化为求△ADE与△ABC的相似比.解法1与解法2都是这样做的,它们只是在求相似比的方法上有所不同.

解法1的思路是通过求两个三角形高之比来求相似比的.因为题中已知了△ABC三边各长,并且I是△ABC的内心,所以可以直接运用△ABC面积的两种表达式来求得两个三角形高之比.

解法2的思路是通过求两个三角形周长之比来求相似比的.因为题中已知了△ABC三边各长,故△ABC周长极易求得,那么就只需求△ADE的周长了,又已知I是△ABC的内心,由切线长定理推论和DE//BC,可以将DE的长转化为DB+EC,从而△ADE周长可通过AD+DB+EC+AE=AB+AC求得,那么就能通过两三角形周长之比求得相似比,从而得到DE的长度.

解法2的巧妙之处在于运用切线长定理推论和DE//BC将DE的长转化为DB和EC后,刚好又分别与AD、AE组合成AB、AC这两条已知了长度的线段,从而可求得△ADE周长.但若I是△ABC的外心或重心等,由于不能使用切线长定理推论,这种巧妙的转化就不复存在,而△ADE三边长都不知道,则只有通过相似比求得△ADE周长,从而又回到之前的问题上,故不能得到解答.因此,解法2的局限性较大,适用范围小.

而解法1更易想到,思路更自然,适用性更广些,若I不是△ABC内心,因的三边长都已知,我们也可以运用海伦公式求得△ABC的面积,从而求得△ABC中BC边上的高,那么就只需求△ADE中DE边上的高了,再充分利用I的性质与特点,想方设法求得△ADE中DE边上的高即可.因此,解法1的基本思路(通过求两个三角形高之比来求相似比,从而求DE的长度)适用范围较大.

四、赛题推广

我们知道三角形不仅有锐角、钝角、直角三角形之分,而且除了内心,还有旁心、外心、垂心、重心.现将此题按照三角形的五心进行推广,每个推广包含各类三角形.其中,推广1、2、5适合初中:而推广3、4的解答因涉及余弦定理,故适合高中.所有的推广运用解法1中的基本思想方法能很容易得到解答.

五、推广的解答

运用解法1中的基本思想方法都能够很好地解答以上五个推广,但由于解答时分类情况较多,且篇幅有限,考虑到推广4的解答难度稍大些,且解法2不能解答该推广,故以解答推广4为例,展示如何用解法1中的基本思想方法来解答,并简要说明为何不能用解法2的思路.有兴趣的读者可以根据解法1的基本思路解答其他推论.

推广4:△ABC中,AB=c,BC=a,CA=b,过△ABC的垂心I作I作DE//BC,分别与AB、AC相交于点D、E,则DE的长为

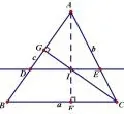
图3

解: ①若△ABC为锐角三角形.

②若△ABC为钝角三角形.

1°若∠A是钝角.

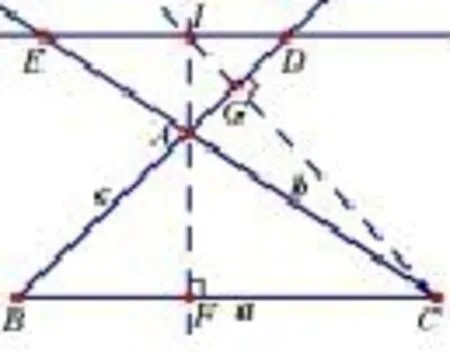
图4

2°若∠C是钝角.

如图5,连接IA交BC延长线于F,连接IC并延长交AB于G.因为I为△ABC的垂心,所以AF⊥BC,CG⊥AB.因为∠IAG=∠BAF,∠AGI=90°=∠AFB,

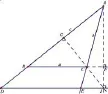
图5

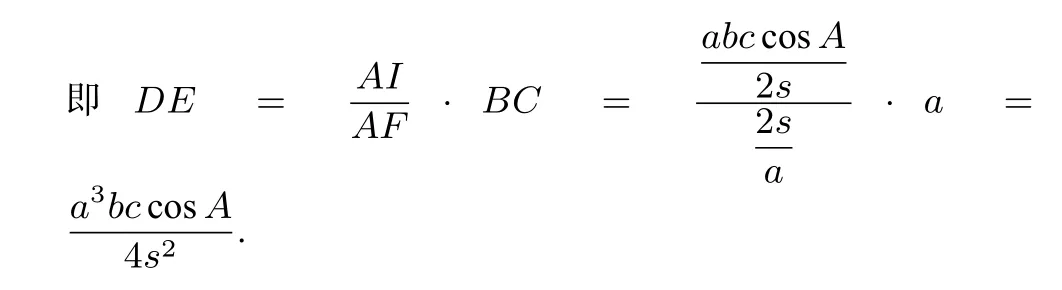
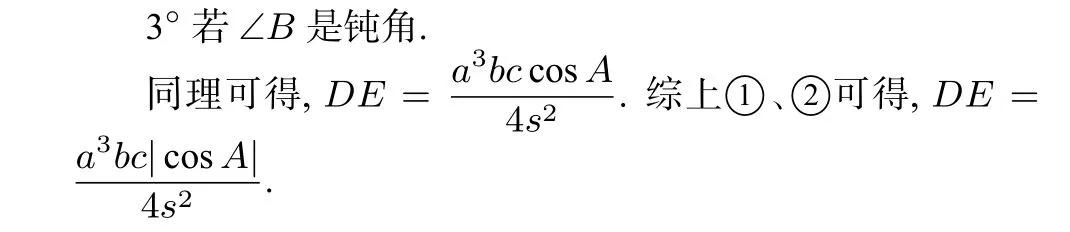
③若△ABC为直角三角形.

1°若∠A是直角.

如图6,则点A为△ABC的垂心,即I与A重合,则D,E均落在A点,那么DE=0.另一方面,当∠A=90°时,cosA=0,故该情况下DE的长度也满足该式子.

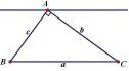
图6

2°若∠C是直角.

3°若∠B是直角.

图7

推广4是运用解法1的基本思路(通过求两个三角形高之比来求相似比)来解答的,难度在于求△ADE的高,此难点是通过充分利用I是△ABC垂心的性质和特点来突破的.

由于I是△ABC垂心,不能使用切线长定理推论,所以解法2中巧妙的转化就不复存在,根据前面第三部分对原题解法的分析可以知道不能用解法2的思路来解答.

六、教学启示

《普通高中数学课程标准(实验)》指出,在基础知识、基本技能的教学中,应注意揭示数学的本质,加强知识间的有机联系.因此,在研究具体问题时应注重剖析其本质,抓住问题的关键,从而强化本质和形式之间的内在结构,深化知识纵横联系.结合自己对此竞赛题推广与解答的经历,我对如何提高解题教学的效益有了一些思考,望与读者分享.

(1.理性对待“通法”与“巧法”,注重挖掘问题本质

相比于解法1,解法2确实较巧妙且计算量小,但正由于它的巧妙,所以对条件或结论要求较苛刻,有时稍微改变(如,推论3、4、5将I改为外心或垂心等等),就不能用此法了,局限性大,不利于学生举一反三.并且“巧法”也有可能掩盖基本思想方法的渗透,故适用范围小.若教师只重视对此法的讲授,则学生很容易出现“懂而不会”的现象.当然,“巧法”也有利于扩展学生解题思路,提高其分析、解决问题的能力.因此,进行解题教学时,教师可以向学生展示“巧法”,但应向学生说明此法的利弊及适用范围,让学生对此有清楚认识,不至于盲目使用.

笔者认为解法1是通法,通过分析发现解法1的思路是基于问题本质(求△ADE中DE边上的高)而产生的,它蕴含了基本思想方法(通过求两个三角形高之比来求相似比),具有普适性,因此,无论将I改为外心、垂心还是重心,无论△ABC是什么三角形,都可以运用此法的解题思路来解决,有利于学生触类旁通,避免陷入“题海战术”,从而提高学习效率.

我认为解题教学不仅仅是就解题而教学,而是应该挖掘问题的本质,尽量讲授能反映问题本质的解法,即通法,揭示通法中的基本思想方法,便于学生理解并掌握,以便学生举一反三.

(2.纵向、横向推广,深化知识联系

将原题按照三角形的五心进行推广,并不限三角形类别.这一系列推广及其解答将平行线的性质、相似三角形、三角形五心的性质、切线长定理推论、圆周角与圆心角的关系、余弦定理等知识紧密联系在一起,形成知识网络,更便于学生理解,从而巩固和强化对知识的掌握,提高学生举一反三的能力.

教师应注意引导学生纵向挖掘、横向延伸相关知识,形成知识网络,帮助学生理解知识的发生发展过程,从而更加深刻地理解其本质.因此,在解题教学时,应适时引导学生进行一题多变、多题一解,并适当进行引申、推广,加强学生对知识、方法的迁移与内化,从而提高数学解题的能力,引申、推广就是找出一些特殊问题中所蕴含的事物发展的规律性,通过合情推理或演绎推理获得更广泛的新结论,在这过程中,学生不仅能体会成功的喜悦,而且有利于创新能力的提高,从而增强探索未知世界的信心.

七、结语

将一个竞赛题横向、纵向进行了五次推广,涉及相似三角形、三角形五心的性质、三角形面积求法、余弦定理等平面几何中关于三角形的大部分知识点,运用原竞赛题解法1的基本思路很容易证明这五个推广,达到了触类旁通的目的,这再次说明了在解题教学中,教师注重讲授通法的重要性.

解法2虽然能简化解题过程且计算量小,还能扩展学生的思维,但在实际运用中,却不能证明以上某些推广(如推广3、4、5),实用范围小.“巧法”的巧妙之处正是建立在严苛的条件或结论之上的,一旦稍有改变,该方法可能行不得通了,故用“巧法”提高学生解题能力的效益不大.

在解题教学时,教师应重点剖析问题的本质,注重基于问题本质进行解题,暴露思维过程,之后,要引导学生进行反思,总结通性通法.可以适时从通法的回顾和反思中,去自然地发现和提炼“巧法”.在此基础上,可适当将问题横向、纵向挖掘进行变式、推广,拓宽问题的宽度,加深问题的深度:引导学生在“变”中发现“不变”的本质,从“不变”的本质中探索“变”的规律,增强学生的创新意识,培养学生思维的深刻性和广阔性.