基于离子交换跃迁模型和实验法对离子液体Walden乘积的研究

郑 玲 潘 懿 季宏祥 马晓雪,3,* 邢楠楠 关 伟,2,*

(1辽宁大学化学院，沈阳110036；2辽宁大学环境学院，沈阳110036；3中国科学院化学研究所，北京分子科学国家实验室，北京100190)

基于离子交换跃迁模型和实验法对离子液体Walden乘积的研究

郑 玲1潘 懿1季宏祥1马晓雪1,3,*邢楠楠1关 伟1,2,*

(1辽宁大学化学院，沈阳110036；2辽宁大学环境学院，沈阳110036；3中国科学院化学研究所，北京分子科学国家实验室，北京100190)

提出了关于离子液体的新理论——离子交换跃迁模型，通过理论推导得出1:1型离子液体的Walden乘积仅取决于离子对和离子簇直径的统计平均值，即离子液体的阴阳离子结构不同，Walden乘积不同。为了验证模型的正确性，本文合成8种N-烷基-吡啶二氰胺类和N-烷基-咪唑丝氨酸类离子液体，利用上述离子液体的电导率和动力粘度的实验值及文献数据，计算了33种离子液体的Walden乘积。通过比较发现，不同离子液体的Walden乘积不同，即对于离子液体来说，Walden乘积是它的特征物理量。

离子液体；电导率；粘度；跃迁模型；Walden乘积

1 引言

离子液体作为液体软材料而受到学术界和工业界的高度关注。近些年，含离子液体的体系已被广泛研究，科研工作者在含有离子液体的体系中得到不同的纳米结构颗粒，如胶束、乳化剂、微乳剂、凝胶剂和囊泡1。常见的离子液体阳离子通常为咪唑、吡啶、季铵盐、季磷盐和一些新型离子液体2－5，由于它们具有特殊性质如难挥发、热稳定性好、可溶解多种有机和无机物，也具有吸收二氧化碳和二氧化硫的能力，无论在提取芳香杂环硫化物、溶解纤维素和木质素、作为锂电池的电解液、光谱分析，还是增强酶活性、控制电化学合成方面都有应用，此外也用于生物膜模型和反应溶剂6－9。电导率和粘度等迁移性质作为离子液体工业化的重要物理化学基础数据，二者间的关系服从Walden规则，即可用Walden乘积(W)将离子液体的摩尔电导率和粘度联系起来。

目前学术界对于Walden乘积是否为常数的观点存在分歧，Angell10和Schreiner11等认为Walden乘积是一个常数，而Wang等12指出，如果所考察的离子液体的阴离子不同，其Walden乘积不同，即Walden乘积不是常数。为了探究Walden乘积是否为一个常数，我们在前期工作13,14的基础上，合成了8种吡啶和咪唑类离子液体，测定了它们不同含水量时的电导率和动力粘度，并进一步得到纯离子液体的电导率和动力粘度值，根据Walden规则计算了它们以及其它25种离子液体的Walden乘积的实验值。同时我们也提出离子液体的离子交换跃迁模型，并对该模型的理论推导结果与实验计算值结合分析，发现二者得到的结论一致，即不同离子液体的Walden乘积不同，Walden乘积是离子液体的特征物理量。

2 实验部分

2.1 试剂与仪器

阴离子交换树脂(纯度＞95%，用常规方法活化)，吡啶(纯度＞99.9%)、1-溴代烷烃(纯度＞99.9%)、二氰胺钠(纯度＞99%)、硝酸银(纯度＞99%)、乙酸乙酯(纯度＞99.9%)、丝氨酸(纯度＞99.9%)、乙腈(纯度＞99.5%)、卡尔费休试剂(纯度＞99%)，以上试剂均购于沈阳化学试剂国药控股有限公司；N-甲基咪唑(购于浙江双港化工厂，使用前用氮气保护进行减压蒸馏)，去离子水(蒸馏得到)。

2.2 离子液体[Cnpy][DCA](n=2－6)和[Cnmim][Ser](n=2－4)的合成

根据文献11,14,15方法分别合成了五种吡啶系列离子液体[C2py][DCA]、[C3py][DCA]、[C4py][DCA]、[C5py][DCA]、[C6py][DCA]和三种咪唑系列离子液体[C2mim][Ser]、[C3mim][Ser]、[C4mim][Ser]，其化学结构及合成反应方程式如图1所示。

合成产物分别采用核磁共振谱仪(Varian-Mercury Plus-300M)对从产物进行核磁共振氢谱(1H NMR)和核磁共振碳谱(13C NMR)的表征，经核磁共振谱分析没有发现杂质共振峰，并采用差示扫描量热仪(Mettler-Toledo)对样品进行热分析实验(见图S1－S24(Supporting Information))，其中，吡啶系列离子液体经高效液相色谱(Agilent)分析其纯度(质量分数)依次为：99.32%、99.71%、99.67%、98.49%和99.02%(见图S25－S29(Supporting Information))。

2.3 电导率和粘度的测定

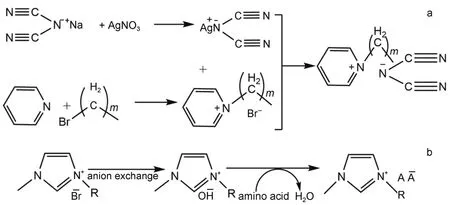
图1 离子液体(ILs)[Cnpy][DCA](n=2－6)和[Cnmim][Ser](n=2－4)的制备过程Fig.1 Synthesized process of ionic liquids(ILs)[Cnpy][DCA](n=2－6)and[Cnmim][Ser](n=2－4)

本文使用MP522型精密电导率仪，对系列N-烷基-吡啶二氰胺离子液体[Cnpy][DCA](n=2－6)和1-烷基-3-甲基咪唑丝氨酸离子液体[Cnmim][Ser]的电导率进行测定。MP522型精密电导率仪的测量精确度为±0.5%FS，控温精确度为±0.4 K，在0.95置信水平，电导率的实验扩展不确定度为±0.21 mS·cm－1，实验测定前用标准液进行校正，校正结果与标准液参数一致。系列离子液体的动力粘度采用微量粘度计(Anton Paar Lovis 2000M)进行测定，仪器的扩展不确定度(0.95置信水平)U(η)= 0.005，仪器在使用前经粘度标准油(N26)进行标定。由于离子液体中微量的水难以去除，本文采用标准加入法16,17，在298.15－338.15 K范围内测定两种不同系列离子液体不同含水量的电导率和粘度(见表S1、S2(Supporting Information))。

实验前，采用SFY-3000型微量水分测定仪分别测定[Cnpy][DCA](n=2－6)和[Cnmim][Ser](n= 2－4)的含水量w2(w2为质量分数)，测定结果显示，[Cnpy][DCA](n=2－6)的含水量均小于0.15%，[Cnmim][Ser](n=2－4)的含水量均小于0.5%。

3 结果与讨论

3.1 电导率和粘度

在298.15－338.15 K范围内测定两种不同系列离子液体不同含水量的电导率和粘度(见表S1、S2)，通过线性外推法得到不含水的系列离子液体在不同温度下的电导率值和粘度值，相关数据及文献值18,19分别列于表1和表2中。

为了探究N-烷基-吡啶二氰胺离子液体和烷基咪唑丝氨酸离子液体的电导率值随温度的变化情况，本文利用Vogel-Tammann-Fulcher(VTF)方程20－22对二者之间的关系进行讨论，VTF方程如下：

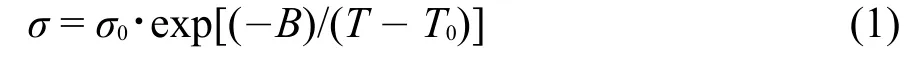
式中，σ为电导率，σ0、B和T0均为拟合参数。根据VTF方程，将不含水时的电导率实验值对温度做非线性拟合，拟合图见图2。

从图2中可知，离子液体的电导率值随温度的升高而逐渐增大，且随着温度的逐渐升高，其电导率值增大的趋势显著。结合表1中不含水时[Cnpy][DCA](n=2－6)或[Cnmim][Ser](n=2－4)的电导率值及图2，即可发现，对于阴离子相同的离子液体，随着离子液体阳离子烷基支链碳原子数的增加，其电导率值逐渐减小。

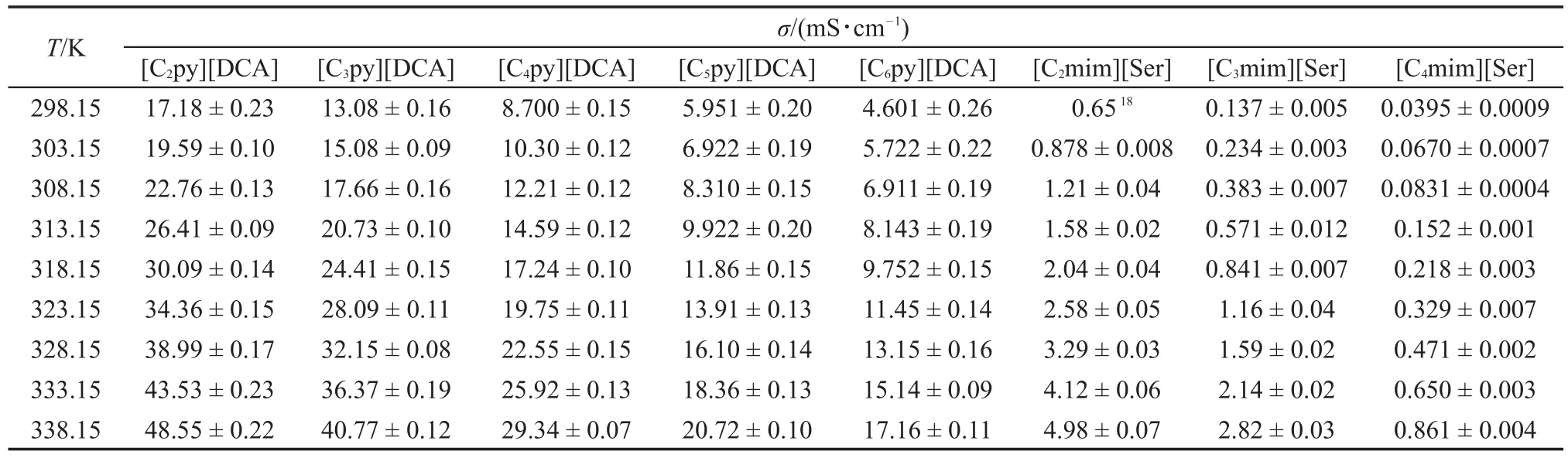
表1 在压力(p)为0.1 MPa，温度298.15－338.15 K范围内[Cnpy][DCA](n=2－6)和[Cnmim][Ser](n=2－4)的电导率(σ)值Table 1 Values of conductivity(σ)for[Cnpy][DCA](n=2－6)and[Cnmim][Ser](n=2－4)at temperature range of 298.15－338.15 Kaand pressure(p)of 0.1 MPab

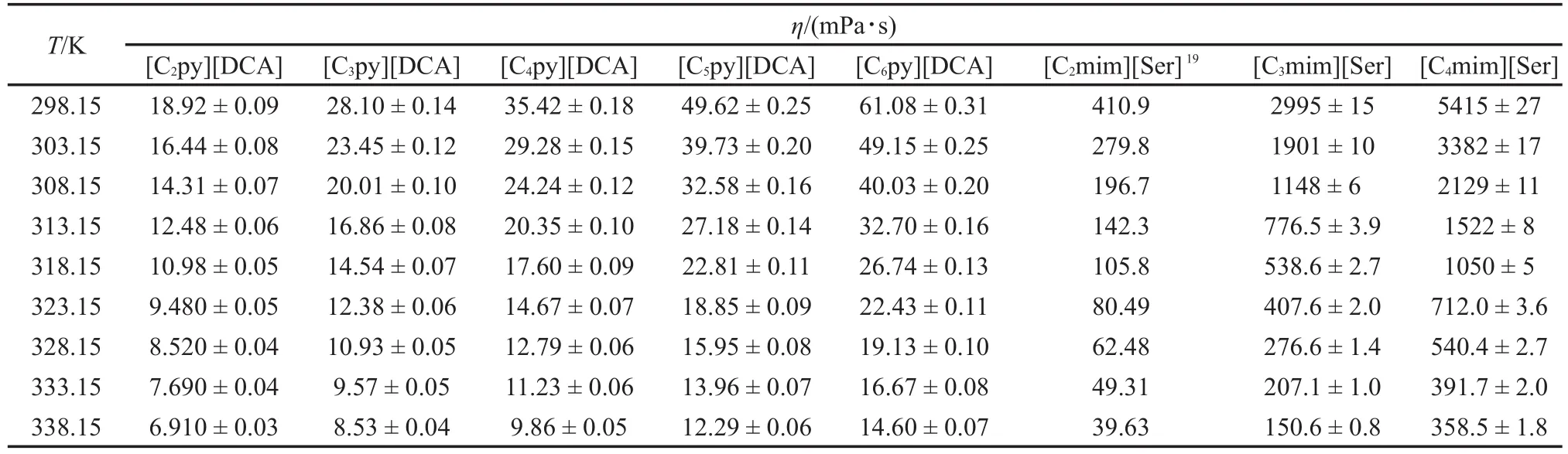
表2 在压力(p)为0.1 MPa，温度298.15－338.15 K范围内[Cnpy][DCA](n=2－6)和[Cnmim][Ser](n=3－4)的粘度(η)值Table 2 Values of dynamic viscosity(η)for[Cnpy][DCA](n=2－6)and[Cnmim][Ser](n=3－4)at temperature range of 298.15－338.15 Kaand pressure(p)of 0.1 MPab

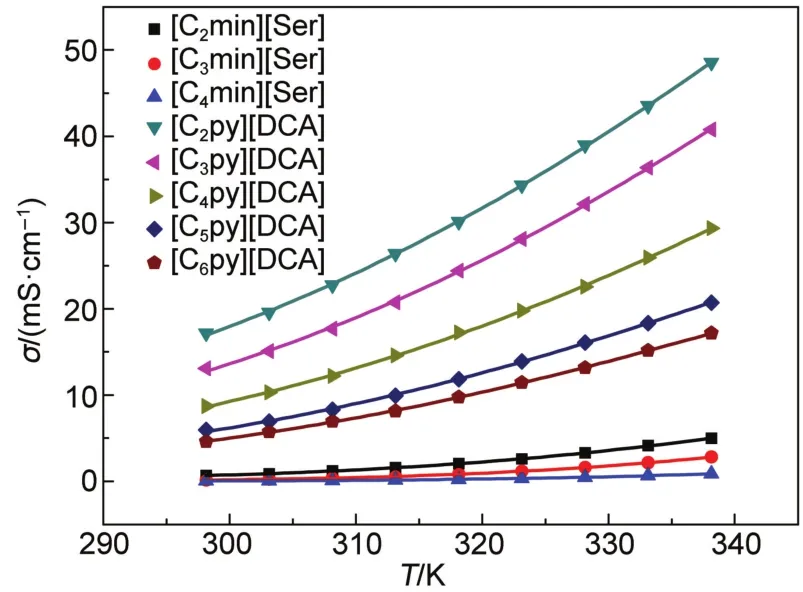
图2 [Cnpy][DCA](n=2－6)和[Cnmim][Ser](n=2－4)的电导率对温度作图Fig.2 Plots of σ vs T for[Cnpy][DCA](n=2－6)and [Cnmim][Ser](n=2－4)

为了探究离子液体的粘度值随温度的变化情况，本文利用VTF方程对二者之间的关系进行讨论，VTF方程如下：

式中，η为动力粘度(mPa·s)，η0、B和T0均为拟合参数。根据VTF方程，将不含水时的粘度实验值对温度做非线性拟合，见图3。从图中可知，离子液体的粘度值都随温度的升高而逐渐减小，且随着温度的逐渐升高，其粘度值减小的趋势越不显著。结合表2中不含水时的粘度值及图3，即可发现，对于同系列离子液体，随着离子液体阳离子烷基支链碳原子数的增加，其粘度值逐渐增大。

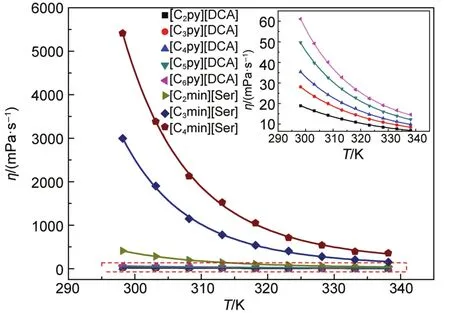
图3 [Cnpy][DCA](n=2－6)和[Cnmim][Ser](n=2－4)的粘度对温度作图Fig.3 Plots of η vs T for[Cnpy][DCA](n=2－6)and [Cnmim][Ser](n=2－4)

摩尔电导率Λ(S·m2mol－1)，是离子液体最重要的迁移性质之一，其定义式如下：

式中，σ(mS·cm－1)是电导率，V(cm3·mol－1)是摩尔体积。根据离子液体的电导率及摩尔体积值可计算得到摩尔电导率值，相关数据和计算结果列于表3。我们通过对两种离子液体的摩尔电导率和粘度实验数据对比发现，吡啶二氰胺类离子液体的摩尔电导率值较大，导电能力较强，并且粘度值较小又表明其具有较低的黏滞力，即流动性较好。通过与文献中离子液体的粘度与摩尔电导率值(见表3)对比可以发现，咪唑二氰胺类离子液体的摩尔电导率较高，且阴离子为二氰胺或双三氟甲基磺酸亚胺的离子液体粘度值较低，均具有较好的流动性。

3.2离子交换跃迁模型

为了探究离子液体的Walden乘积是否为一个特征物理参数，本文提出了一个新的理论模型——离子液体离子交换跃迁模型，该模型的提出基于以下三点：

(1)离子液体通常是体积大的，不对称的阴离子和阳离子所组成的液态有机盐。离子液体中存在自由离子、离子对和离子簇，但是由于阴离子和阳离子间存在库仑力作用，即离子液体中离子对和离子簇的数量较多。

(2)在电场作用下，离子对或离子簇沿外电场方向做定向运动。

(3)在粘滞的离子液体中，对于某一个体积大而又不对称的离子很难从一个电极迁移到另一个电极，也就是说离子液体的电导是通过离子交换跃迁完成的。事实上，电导率是在离子簇中以离子交换跃迁的链转移过程完成的。阳离子具体是怎样完成交换跃迁过程的，可以用如下的示意图来解释：

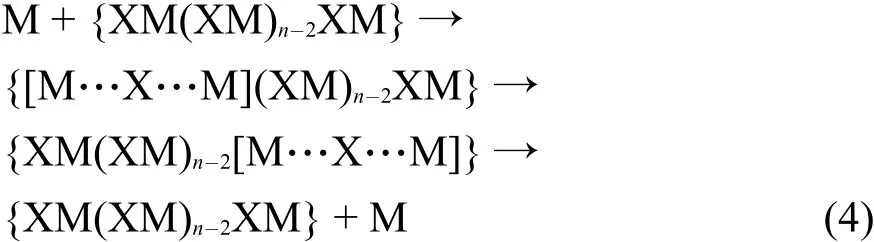
在离子簇中，上式中M代表阳离子，XM代表离子对，X代表阴离子，下角标“n”代表离子对(M与X)中的数量，[M…X…M]代表过渡态。假设在离子簇中，自由阳离子M从左侧加入到第一个离子对XM，这样，在该离子簇的右侧可以形成一个过渡状态，即{[M…X…M](XM)n－2XM}。紧接着在这个离子簇中，存在于第一个XM中的阳离子(M)在右边形成了一个新XM，然而此离子簇中原本的M离开，即{XM(XM)n－2XM}+M，以形成一个新的自由阳离子。新形成的自由阳离子再接续进入下一个离子对中，以上述方式这样依次进行，形成过渡态。新的自由阳离子持续的发生迁移，直至最后一个新的阳离子脱离离子簇为止。因此，离子完成交换跃迁等同于一个自由阳离子从左至右的运动过程。

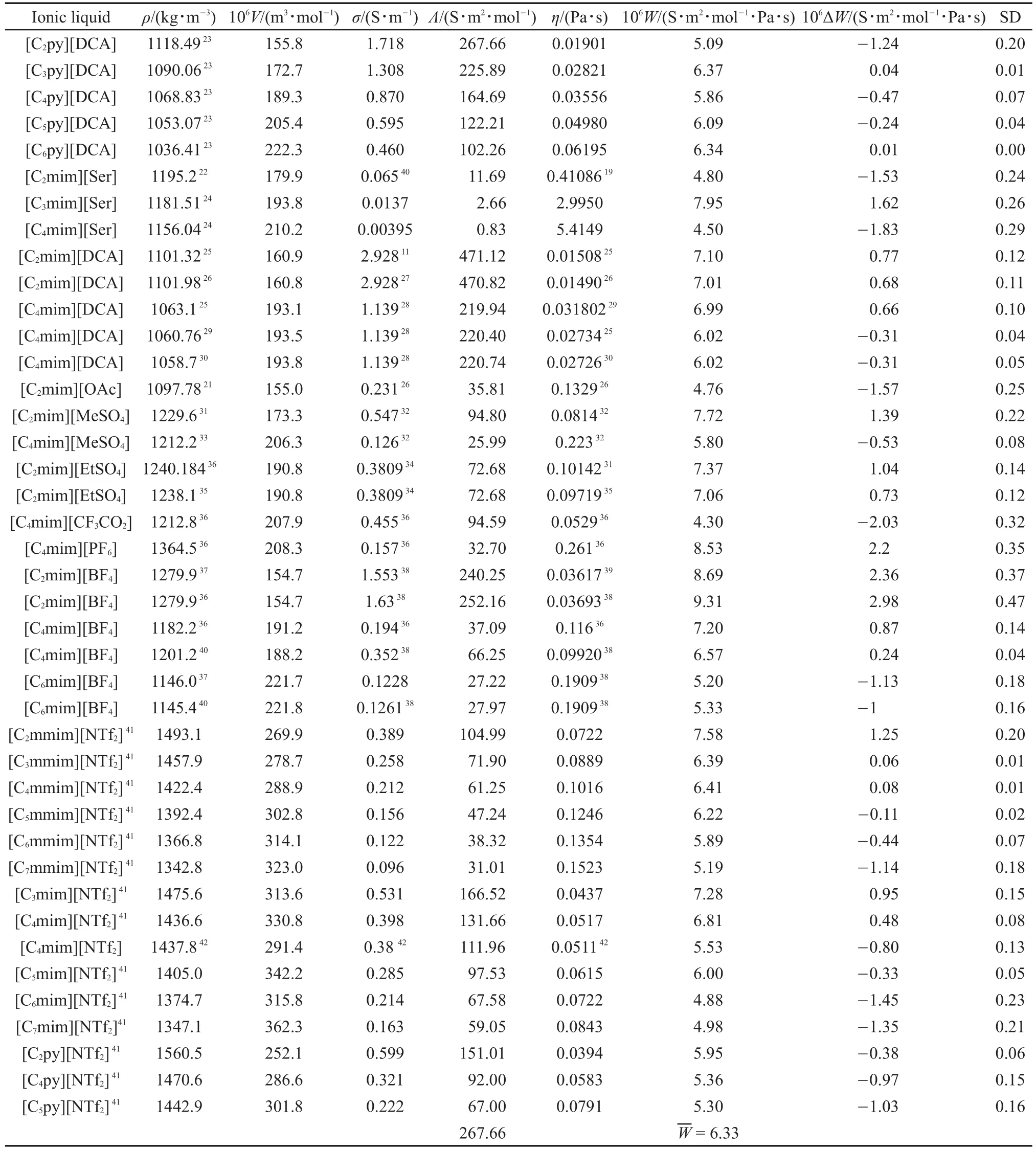
表3 在298.15 K时不同离子液体的Walden乘积及相关性质参数Table 3 Values of relative physical variables and Walden products for different ILs at 298.15 K

离子交换跃迁的基元过程即是对于自由阳离子(M)沿电场方向运动和离子对(XM)沿电场方向重排的过程：

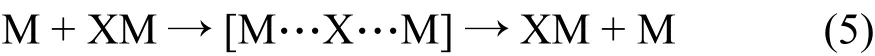
在这个基元过程中，存在一个过渡状态[M…X…M]。在电场中，阳离子(M)沿电场方向移动了ξ距离(ξ等于离子对MX的直径)。ΔG是M迁移完成所做的功，即该过程的吉布斯自由能的差值。其中一部分的功ξΔG是在始态时吉布斯自由能的增量，另外一部分(1－ξ)ΔG是在终态时吉布斯自由能的减量。

事实上，因子ξ取决于始态，过渡态和终态[M…X…M]中电子的存在形式。该模型具体描述如下：

在单位时间里迁移的阳离子数，即在电场作用下，阳离子正向迁移的平均速度uf：

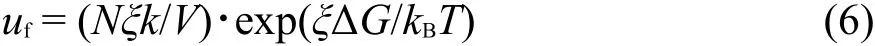
式中，N为Avogadro常数，V为摩尔体积，kB为玻尔兹曼常数，T是热力学温度，k为基元过程的速率常数，根据过渡态理论，速率常数k可以表示为：

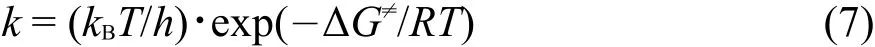
式中，h是Planck常数，R是气体常数，ΔG≠是活化吉布斯自由能。在电场作用下，离子反向迁移的平均速度ub可表示为：

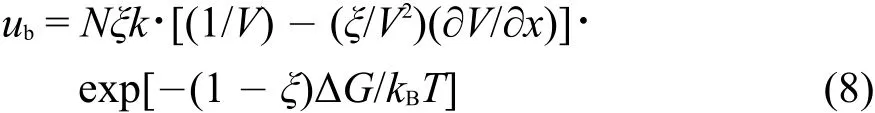
离子i的总平均速度为ui：

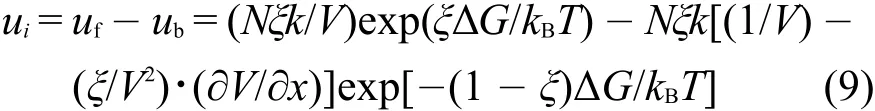
上述等式中的指数可以展开级数。在通常条件下，公式可以被作为一级近似，因为ΔG＜＜kBT。因此，展开级数中的二次项以及高阶项可以被省略。作为一级近似，方程(9)可以转化为：

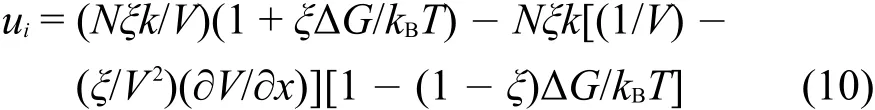
由于(1－ξ)ΔG＜＜1，上述方程可以变为：

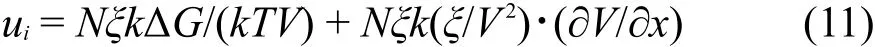
在电场作用下，离子的迁移速度很快，所以第二项的贡献远小于第一项，即可忽略不计。进而等式(11)转化为：

基元迁移的初始状态，离子i做功ΔG表示如下：

在电场中，式中zi是离子的电荷数，e是电子电量，Δφ是电位梯度。

另外，离子的迁移速率与离子淌度Ui之间关系如下：

其中，离子淌度可根据下式计算：

根据Eyring粘度公式：

将方程(17)代入到方程(16)，并整理可得：

式中，F是Faraday常数。根据定义可得到方程(19)：

则离子液体的摩尔电导率：

式中，(z++z－)是离子的电荷数，ξ是离子对和离子簇直径的统计平均值，其值是离子间相互作用力大小的量度。将方程(20)重排并整理可得：

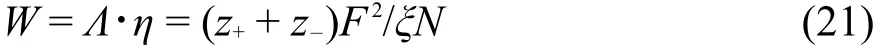
方程(21)表明，对于电荷比为1:1的离子液体，其摩尔电导率与粘度的乘积(Walden)是与离子液体有关的一个参数，Walden乘积取决于离子对和离子簇直径的统计平均值，即对于不同的离子液体来说，其Walden乘积不是常数。这就意味着，不同的离子液体，存在不同的Walden乘积，即Walden乘积是离子液体的物理特征参数。

3.3离子液体的Walden乘积计算

根据离子液体的摩尔电导率和其粘度服从Walden规则：

式中，Λ是摩尔电导率(S·m2·mol－1)，η是动力粘度(Pa·s)，W是Walden乘积(S·m2·mol－1·Pa·s)。利用公式(22)计算了[Cnpy][DCA](n=2－6)和[Cnmim] [Ser](n=2－4)以及25种离子液体的Walden乘积。同时将文献11,18,19,21－42中报道的25种离子液体的相关性质参数及计算得到Walden乘积和Walden乘积的标准偏差均列于表3中。

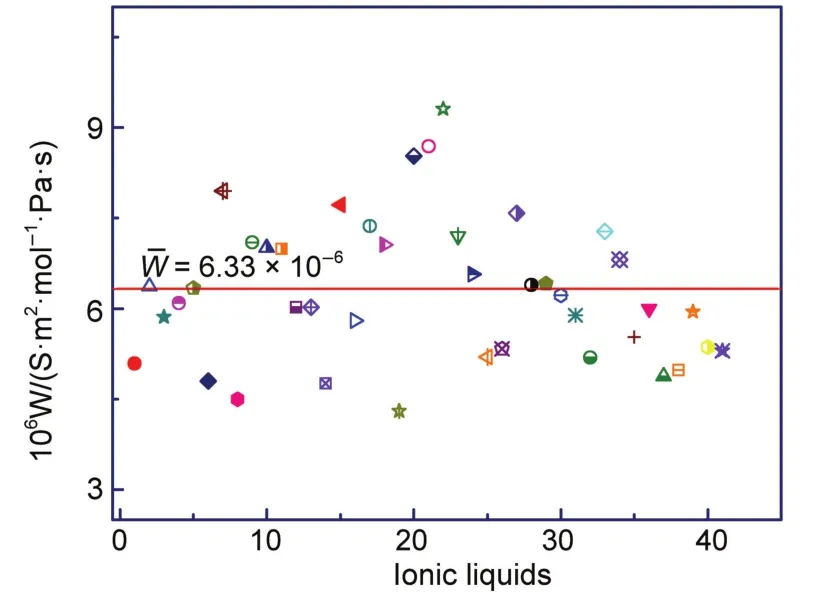
图4 33种离子液体的Walden乘积Fig.4 Walden products of 33 kinds of ionic liquids color online

4 结论

本文成功合成8种N-烷基-吡啶二氰胺类和N-烷基-咪唑丝氨酸类离子液体，测定了离子液体的电导率和动力粘度。同时提出了离子液体离子交换跃迁模型，结果表明对于1:1型的离子液体其Walden乘积取决于离子对和离子簇直径的统计平均值，也就是说，组成离子液体的阴阳离子结构不同，它们的Walden乘积不同。为验证该结论的正确性，我们计算了33种离子液体的Walden乘积，结合实验数据与文献数据发现，Walden乘积近似相等但不是一个常数。实验结果与离子液体离子交换跃迁模型得到的结论一致，即对于不同离子液体来说Walden乘积不同，Walden乘积是它的特征物理量。

Supporting Information:available free of charge via the internet at http://www.whxb.pku.edu.cn.

(1) Kang,X.C.;Sun,X.F.;Zhu,Q.G.;Ma,X.X.;Liu,H.Z.;Ma, J.;Qian,Q.L.;Han,B.X.Green Chem.2016,18,1869. doi:10.1039/C5GC02848E

(2) Liu,Q.S.;Liu,H.;Mou,L.Acta Phys.-Chim.Sin.2016,32(3), 617.[刘青山,刘 惠,牟 林.物理化学学报,2016,32(3), 617.]doi:10.3866/PKU.WHXB201512171

(3) Liu,Q.S.;Yan,P.F.;Yang,M.;Tan,Z.C.;Li,C.P.;Welz-Biermann,U.Acta Phys.-Chim.Sin.2011,27(12),2762.[刘青山,颜佩芳,杨 淼,谭志诚,李长平,Welz-Biermann,Urs.物理化学学报,2011,27(12),2762.]doi:10.3866/PKU. WHXB20112762

(4) Padró,J.M.;Reta,M.J.Mol.Liq.2016,213,107.doi:10.1016/ j.molliq.2015.10.055

(5) Yang,X.;Song,H.;Wang,J.;Zou W.RSC Adv.2016,6,29172. doi:10.1039/C5RA27934H

(6) Calvar,N.;Gomez,E.;Macedo,E.A.;Dominguez,A. Thermochim.Acta 2013,565,178.doi:10.1016/j. tca.2013.05.007

(7) Crosthwaite,J.M.;Muldoon,M.J.;Dixon,J.K.;Anderson,J. L.;Brennecke,J.F.J.Chem.Thermodyn.2005,37,559. doi:10.1016/j.jct.2005.03.013

(8) Zhao,D.B.;Fei,Z.F.;Geldbach,T.J.;Scopelliti,R.;Dyson,P. J.J.Am.Chem.Soc.2004,126(48),15876.doi:10.1021/ ja0463482

(9) Yunus,N.M.;Mutalib,M.I.A.;Man,Z.;Bustam,M.A.; Murugesan,T.Chem.Eng.J.2012,189,94.doi:10.1016/j. cej.2012.02.033

(10) Xu,W.;Cooper,E.I.;Angell,C.A.J.Phys.Chem.B 2003,107, 6170.doi:10.1021/jp0275894

(11) Schreiner,C.;Zugmann,S.;Hartl,R.;Gores,H.J.J.Chem. Eng.Data 2010,55,4372.doi:10.1021/je1005505

(12) Xu,A.;Zhang,Y.;Li,Z.;Wang,J.J.;J.Chem.Eng.Data 2012, 57,3102.doi:10.1021/je300507h

(13) Zheng,L.;Fan,B.H.;Bu,X.X.;Pan,Y.;Dong,J.X.;Guan,W. Acta Phys.-Chim.Sin.2015,31(11),2036.[郑 玲,樊本汉,卜晓雪,潘 懿,董家新,关 伟.物理化学学报,2015,31(11), 2036.]doi:10.3866/PKU.WHXB201509111

(14) Bu,X.X.;Fan,B.H.;Wei,J.;Xing,N.N.;Ma,X.X.;Guan,W. Acta Phys.-Chim.Sin.2016,32(1),267.[卜晓雪,樊本汉,魏杰,邢楠楠,马晓雪,关 伟.物理化学学报,2016,32(1), 267.]doi:10.3866/PKU.WHXB201510303

(15) Zhang,S.G.;Qi,X.J.;Ma,X.Y.;Lu,L.J.;Deng,Y.Q.J.Phys. Chem.B 2010,114,3912.doi:10.1021/jp911430t

(16) Guan,W.;Ma,X.X.;Li,L.;Tong,J.;Fang,D.W.;Yang,J.Z. J.Phys.Chem.B 2011,115,12915.doi:10.1021/jp207882t

(17) Ma,X.X.;Wei,J.;Zhang,Q.B.;Tian,F.;Feng,Y.Y.;Guan,W. Ind.Eng.Chem.Res.2013,52,9490.doi:10.1021/ie401130d

(18) Fukumoto,K.;Yoshizawa,M.;Ohno,H.J.Am.Chem.Soc. 2005,127,2398.doi:10.3390/molecules15042388

(19) Muhammad,N.;Man,Z.B.;Bustam,M.A.;Mutalib,M.I.A.;Wilfred,C.D.;Rafiq,S.J.Chem.Eng.Data 2011,56,3157. doi:10.1021/je2002368

(20) Tokuda,H.;Hayamizu,K.;Ishii,K.;Susan,M.A.B.H.; Watanabe,M.J.Phys.Chem.B 2005,109,6103.doi:10.1021/ jp044626d

(21) Tokuda,H.;Tsuzuki,S.;Susan,M.A.B.H.;Hayamizu,K.; Watanabe,M.J.Phys.Chem.B 2006,110,19593.doi:10.1021/ jp064159v

(22) Wu,T.Y.;Su,S.G.;Gung,S.T.;Lin,M.W.;Lin,Y.C.;Lai,C. A.;Sun,I.W.Electrochim.Acta 2010,55,4475.doi:10.1016/j. electacta.2010.02.089

(23) Ma,X.X.;Wei,J.;Guan,W.;Pan,Y.;Zheng,L.;Wu,Y.;Yang, J.Z.J.Chem.Thermodyn.2015,89,51.doi:10.1016/j. jct.2015.02.025

(24) Wei,J.;Chang,C.;Zhang,Y.;Hou,S.;Fang,D.;Guan,W. J.Chem.Thermodyn.2015,90,310.doi:10.1016/j. jct.2015.04.029

(25) Larriba,M.;Navarro,P.;García,J.;Rodríguez,F.Ind.Eng. Chem.Res.2013,52,2714.doi:10.1021/ie303357s

(26) Quijada-Maldonado,E.;Boogaart,S.V.D.;Lijbers,J.H.; Meindersma,G.W.;Haan,A.B.D.J.Chem.Thermodyn.2012, 51,51.doi:10.1016/j.jct.2012.02.027

(27) Villagran,C.;Banks,C.E.;Hardacre,C.;Compton,R.G.Anal. Chem.2004,76,1998.doi:10.1021/ac030375d

(28) Stoppa,A.;Hunger,J.;Buchner,R.J.Chem.Eng.Data 2009, 54(2),472.doi:10.1021/je800468h

(29) Carvalho,P.J.;Regueira,T.;Santos,L.M.N.B.F.;Fernández, J.;Coutinho,J.A.P.J.Chem.Eng.Data 2010,55,645. doi:10.1021/je900632q

(30) Paduszynski,K.;Okuniewski,M.;Domanska,U.J.Phys. Chem.B 2013,117,7034.doi:10.1021/jp401937p

(31) Yang,J.Z.;Lu,X.M.;Gui,J.S.;Xu,W.G.;Li,H.W.J.Chem. Thermodyn.2005,37,1250.doi:10.1016/j.jct.2005.03.002

(32) Andanson,J.M.;Traikia,M.;Husson,P.J.Chem.Thermodyn. 2014,77,214.doi:10.1016/j.jct.2014.01.031

(33) Pereiro,A.B.;Rodriguez,A.J.Chem.Thermodyn.2007,39, 978.doi:10.1016/j.jct.2006.10.017

(34) Li,W.J.;Zhang,Z.F.;Han,B.X.;Yang,G.Y.J.Phys.Chem.B 2007,111,6452.doi:10.1021/jp071051m

(35) Calado,M.S.;Diogo,J.C.F.;Correia da Mata,J.L.;Caetano, F.J.P.;Visak,Z.P.;Fareleira,J.M.N.A.Int.J.Thermophys. 2013,34,1265.doi:10.1007/s10765-013-1491-2

(36) Diogo,J.C.F.;Caetano,F.J.P.;Fareleira,J.M.N.A.; Wakeham,W.A.Int.J.Thermophys.2014,35,1615. doi:10.1007/s10765-013-1487-y

(37) Xu,W.G.;Li,L.;Ma,X.X.;Yang,J.Z.J.Chem.Eng.Data 2012,57,2177.doi:10.1021/je3000348

(38) Rilo,E.;Vila,J.;Pico,J.;Oscar,C.J.Chem.Eng.Data 2010, 55,639.doi:10.1021/je900600c

(39) Huddleston,J.G.;Visser,A.E.;Reichert,W.M.;Willauer,H. D.;Broker,G.A.;Rogers,R.D.Green Chem.2001,3,156. doi:10.1039/b103275p

(40) Rilo,E.;Pico,J.;Garcia-Garabal,S.;Varela,L.M.;Cabeza,O. Fluid Phase Equilibr.2009,285,83.doi:10.1016/j. fluid.2009.07.010

(41) Chen,Z.J.;Lee,J.M.J.Phys.Chem.B 2014,118,2712. doi:10.1021/jp411904w

(42) Zhao,H.;Liang,Z.C.;Li,F.J.Mol.Liq.2009,149,55. doi:10.1016/j.molliq.2009.08.002

Evaluation of the Walden Product of Ionic Liquids Using Experiments and a New Theory:An Ion Exchange Transition Model

ZHENG Ling1PAN Yi1JIHong-Xiang1MAXiao-Xue1,3,*XING Nan-Nan1GUAN Wei1,2,*
(1College of Chemistry,Liaoning University,Shenyang 110036,P.R.China;2School of Environmental Science, Liaoning University,Shenyang 110036,P.R.China;3Beijing National Laboratory for Molecular Sciences, Institute of Chemistry,Chinese Academy of Sciences,Beijing 100190,P.R.China)

Anew theory has been developed to evaluate the Walden product,W,of ionic liquids using an ion exchange transition model.This model showed that the product(Walden)of molar conductivity and dynamic viscosity is related to the average diameters of the ion pairs and ion clusters of ionic liquids(ILs)with 1:1 charge ratios,namely,differentILs have different W values.Several experiments were conducted to evaluate the validity of this model.Eight differentILs,including five N-alkyl-pyridinium dicyanamideILs[Cnpy][DCA](n=2－6)and three N-alkyl-3-methyllimidazolium serineILs[Cnmim][Ser](n=2－4)were successfully synthesized and evaluated in terms of their conductivity and dynamic viscosity properties.The W values of 33 differentILs were calculated based on their experimentally determined molar conductivity and dynamic viscosity values,and the results revealed that these values were consistent with those of the ion exchange transition model.Taken together,these results demonstrate that W is a key physical parameter forILs.

Ionic liquid;Conductivity;Viscosity;Transition model;Walden product

O642

10.3866/PKU.WHXB201607292

Received:June 14,2016;Revised:July 28,2016;Published online:July 29,2016

*Corresponding authors.GUAN Wei,Email:guanweiy@sina.com;Tel:+86-24-62207797.MAXiao-Xue,Email:mxx_1985@163.com;

Tel:+86-24-62207797.

The project was supported by the National Natural Science Foundation of China(21373104,21273003)and Program for Liaoning Excellent Talents in University,China(LR2015025).

国家自然科学基金(21373104,21273003)和辽宁省高等学校优秀人才支持计划(LR2015025)资助项目