微重力双向温差作用下Czochralski法硅熔体中的热毛细对流＊

魏程星云，彭 岚，张全壮

(重庆大学 动力工程学院，低品位能源利用技术及系统教育部重点实验室，重庆 400044)

微重力双向温差作用下Czochralski法硅熔体中的热毛细对流＊

魏程星云，彭 岚，张全壮

(重庆大学 动力工程学院，低品位能源利用技术及系统教育部重点实验室，重庆 400044)

采用数值模拟的方法研究了微重力条件下Czochralski法生长硅晶体过程中熔体热毛细对流的基本特征，探讨了水平和垂直温度梯度的耦合对熔体流动的影响。熔体自由表面与外界辐射换热，水平温度梯度Marangoni(Ma)数选取(0～3 000)，底部热流Q选取(1.39×10-2～1.76×10-2)。结果表明，当Q和Ma数均较小时，流动为稳态，液池内产生3个流胞，熔体流动由Q主导，减小Q或增大Ma数可使流动更稳定。当Ma数增大到一定值时，流动从稳态转变为非稳态，流动的临界Mac数随Q的增大而显著减小。流动失稳后，出现了新的流动转变方式，Ma数为影响表面波动形式的关键因素，Q会改变热流体波数，是晶体附近的热流体波产生的决定因素。随着Ma数和Q的不断增强，自由表面最终形成弯曲条幅状热流体波。

热毛细对流；Cz结构；双向温度梯度；数值模拟;表面张力

0 引 言

硅晶体因其优越的热学、电学、光学等特性被广泛应用于光伏工程、电子技术、航空航天技术等领域。目前，Czochralski生长法(Cz法)是制备硅晶体的最主要的方式之一。在Cz法制备硅单晶的过程中，有两种不同形式的表面张力驱动硅熔体进行流动，一种是水平温度梯度形成的表面张力所驱动的热毛细对流；另一种是垂直温度梯度所驱动的Marangoni对流。这两种流动相互作用，对Cz法生成晶体的质量有着很大的影响。近些年来，许多学者对液池内的热毛细对流进行了大量的研究[1-5]。Kyung-Woo Yi等[6]采用数值模拟的方法，发现热毛细对流会影响Czochralski结构中的流体温度和流动结构的不对称性，并且认为Marangoni-Bénard不稳定性和Rayleigh-Bénard不稳定性是在不同表面张力系数下引起流动失稳的主要原因。Nepomnyashchy[7]最早使用数值模拟方法及线性稳定性理论对微重力条件下的矩形液池内的Bénard-Marangoni对流进行了研究，阐述了垂直和水平的温度梯度的相对大小对液层内的流胞运动方向的影响。Jing等[8]发现Marangoni效应对大尺寸Cz结构内熔体自由表面的波动形式有着决定性的作用。Yao等[9-10]用数值模拟的方法对液桥内的热毛细对流进行研究，结果表明磁场可以很好的抑制热毛细对流，且普朗特数的大小对热毛细对流起着重要的作用。Peng等[11]对方形池内的硅油进行了不同温差下的实验研究，实验结果表明浮力对流可以抑制热毛细对流。Y.Takagi等[12]发现坩埚旋转和磁场相结合对热毛细对流产生的的热流体波有很好的抑制作用。T.Yamamoto等[13]发现通过改变液池的宽深比可以控制熔体内热毛细对流的流动方向。Wang等[14]利用三维数值模拟研究了环形浅液池内垂直温度梯度对硅油热毛细对流的影响，结果表明增加底部热流可以改变自由表面振荡波波形，流动最不稳定的区域在环形池内壁附近。

以往国内外的大部分研究主要集中于Marangoni对流或者热毛细对流单独存在下的情况，很少有研究报道流体中两种流动同时存在的情况，然而在晶体的实际生长过程中由于存在双向温差使得熔体中同时存在着两种流动，称为Marangoni-热毛细对流；并且大部分学者研究的液池均为浅液池，而Cz法制备晶体的坩埚深度一般较深。因此，对双向温差下深液池中的热毛细对流的研究显得尤为重要。为了了解实际过程中双向温差耦合作用对熔体热毛细对流的影响，本文采用有限差分法对Cz法生长硅晶体过程中的热毛细对流进行了三维数值模拟，得出了不同温差和底部热流密度耦合的情况下的硅熔体流动的基本特征，重点分析了水平和竖直方向的温度梯度耦合作用对熔体内部流动的影响。

1 数学物理模型

物理模型如图1所示，坩埚内半径rc=50 mm，晶体半径rs=15 mm，液池深度h=8 mm，坩埚底部以恒定均匀热流q加热，自由边界为不变形的平面且与环境进行辐射换热，坩埚壁维持恒温Th，结晶界面温度为Tc=Tm，水平温差ΔT=Th-Tc。

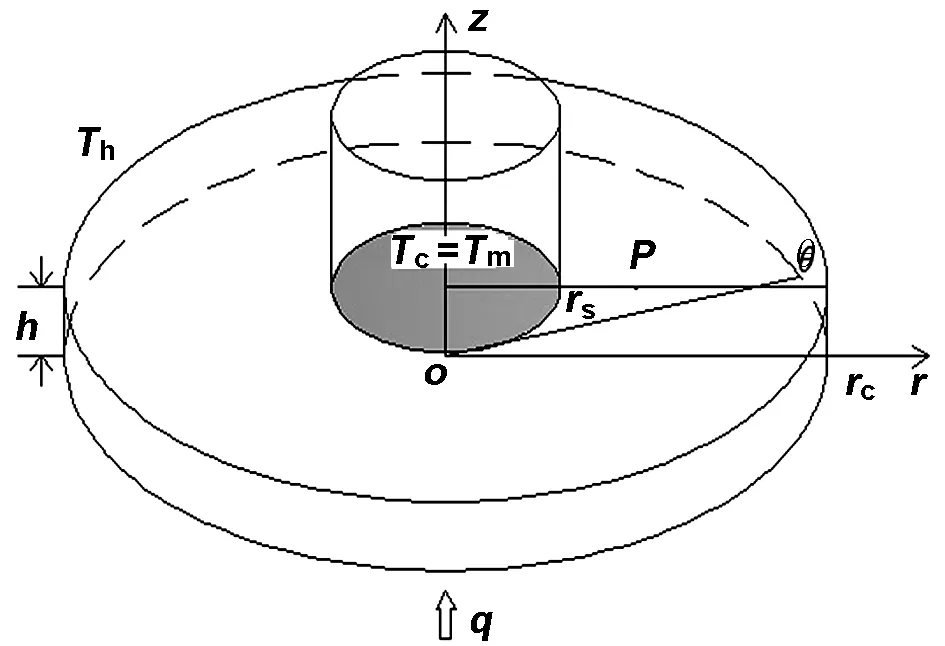
图1 物理模型

为简化计算，作出如下假定：(1) 熔体为不可压缩牛顿流体；(2) 流速较低，流动为层流；(3) 所有固-液界面满足无滑移条件；(4) 液体自由表面平整无变形；(5) 液体自由表面考虑热毛细力的作用并且与外界进行辐射换热。

在上述假定条件下，引入无量纲参数温度

和无量纲热流密度

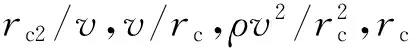
·V=0

(1)

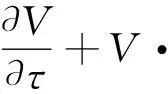
(2)

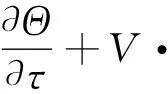
(3)

边界条件为：

自由表面

(4)

(5)

熔体-晶体界面

Z=H,0≤R≤Rs,0≤θ≤2π

Vθ=VR=VZ=0,Θ=1

(6)

坩埚底部

Z=0,0≤R<1,0≤θ≤2π

(7)

坩埚侧壁

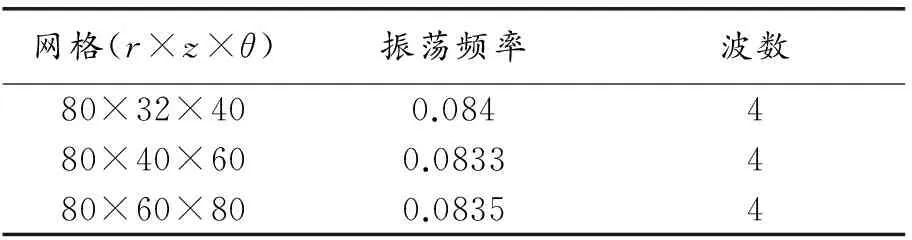
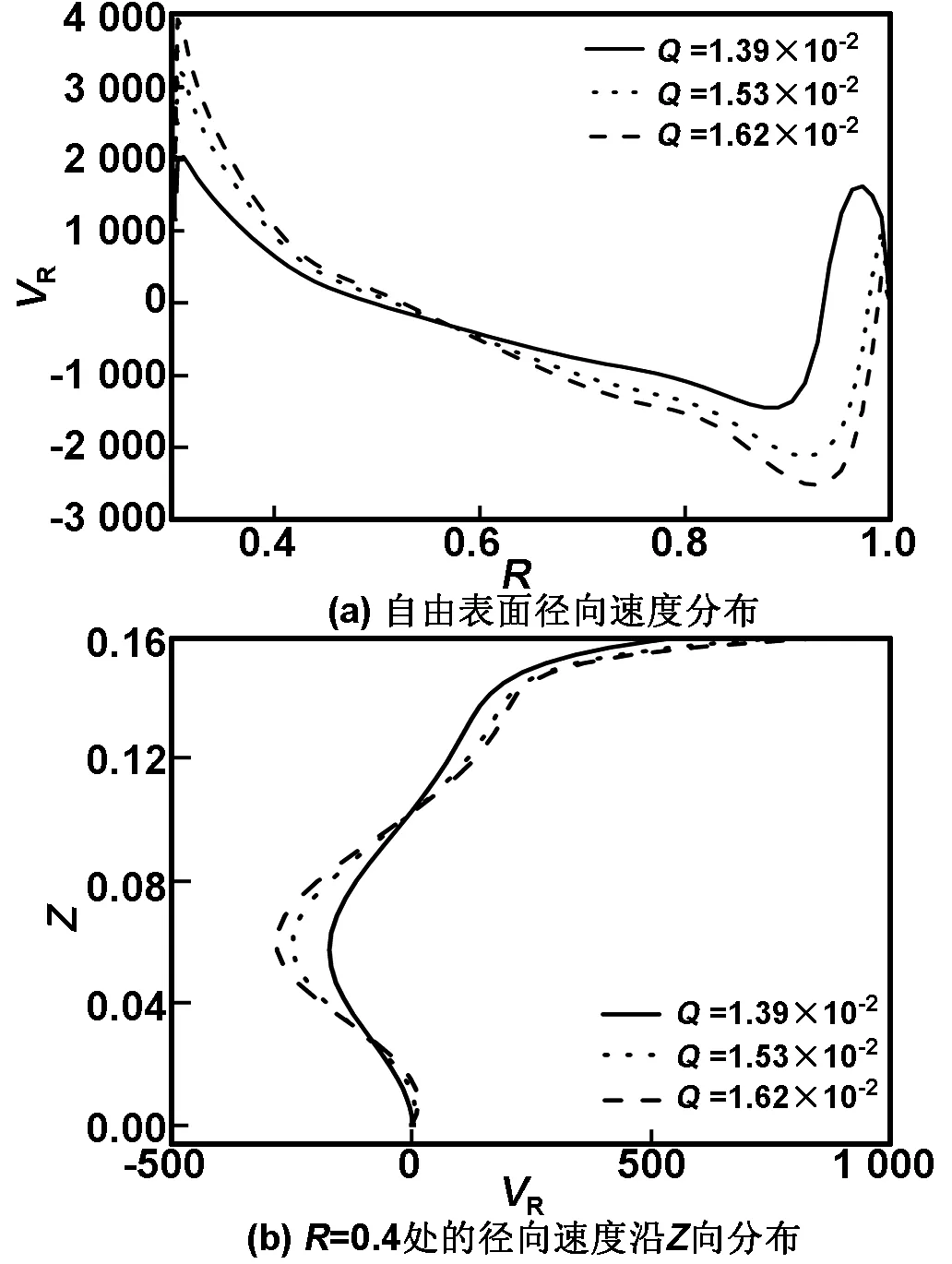
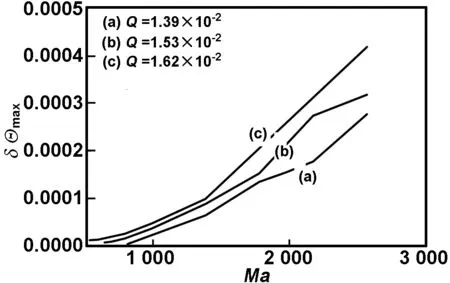
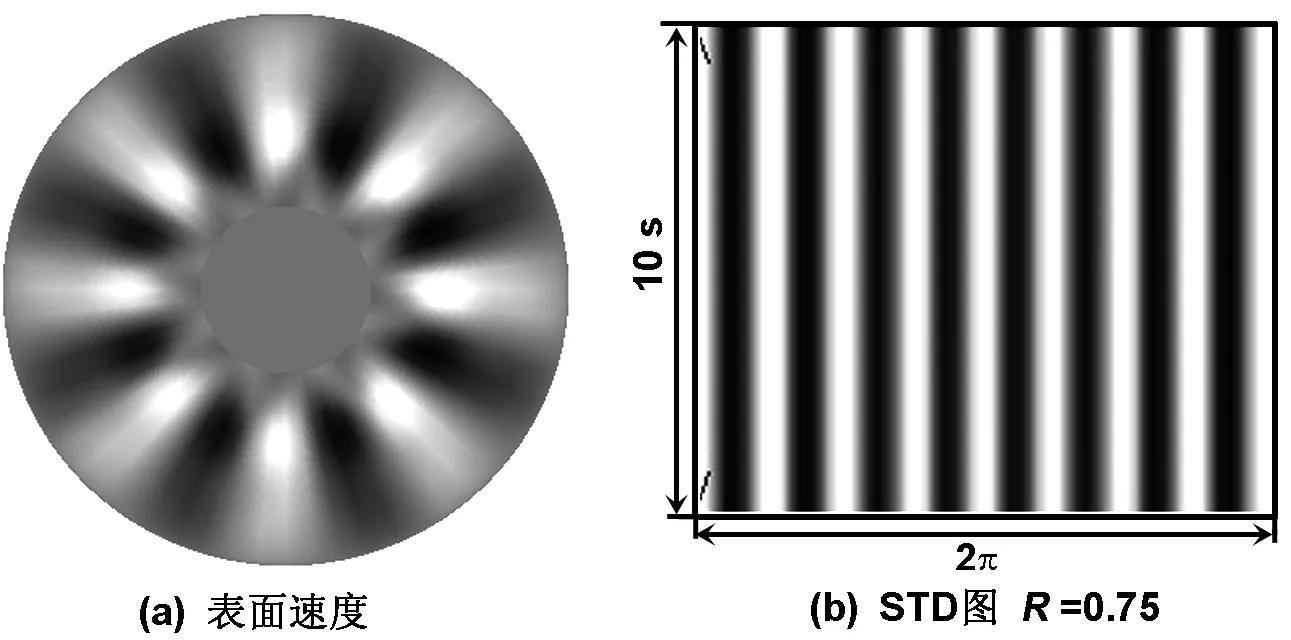
0

Vθ=VR=VZ=0,Θ=Θh

(8)

初始条件(τ=0)

VR=VZ=Vθ=0,

(9)

其中

和

分别为普朗特数，毛细雷诺数和热辐射数。定义Marangoni数为

式中

为表面张力温度系数，v为动量扩散率，α为热扩散率，σ为斯忒藩-玻耳兹曼常数，ε为发射率，λ为导热系数，ρ为熔体密度。熔点温度Tm=1 683 K下硅熔体的物性参数如表1所示。

表1Tm=1 683 K时硅熔体物性参数

Table 1 Physical properties of the silicon melt atTm=1 683 K

参数,符号单位数值表面张力温度系数,γTN/(m·K)-7.0×10-5密度,ρkg/m32530动力粘度,μkg/(m·s)7.0×10-4动量扩散率,vm2/s2.767×10-7比热,CpKJ/(kg·K)1000导热系数,λW/(m·K)64热扩散率,αm2/s2.53×10-5辐射率,ε0.318

利用有限容积法对基本方程进行离散，扩散项采用中心差分，对流项采用QUICK格式，压力-速度修正采用SIMPLE方法，计算采用80r×40z×60θ的非均匀网格，时间步长取为1.19×10-3s，在每个时间步长内，如果控制容积上的最大残差<10-8，则认为计算收敛。计算程序的正确性已被大量的计算结果所证实[15]，网格无关性验证如表2所示，因此计算中选择的网格为80r×40z×60θ。

表2 网格收敛性的检验(Ma=1 581，Q=1.39×10-2)

Table 2 Validation of grid convergence (Ma=1 581，Q=1.39×10-2)

网格(r×z×θ)振荡频率波数80×32×400.084480×40×600.0833480×60×800.08354

2 结果与讨论

2.1 基本流动

当底部热流密度和温差较小时，液池内硅熔体的流动较弱为稳态轴对称流动，竖直平面内的流动流型可用等流函数线表示(图中正、负号分别代表逆时针和顺时针方向)。无因次流函数定义如下

(10)

2.1.1Ma数对基本流的影响

当水平温差较小时，流动为稳态。自由表面的熔体在热毛细力的驱动下从坩埚壁向晶体流动，在熔体中产生逆时针流胞。图2给出了Q=1.53×10-2时，不同Ma数下液池内R-Z平面的等流函数线和等温线分布图。当Ma数较小时，垂直温差主导熔体内部流动，产生了占据主流区的顺时针大流胞。晶体附近的熔体在水平温差作用下形成一个逆时针小流胞，熔体内形成双胞流。随着Ma数增大，左侧小流胞流动增强，右侧大流胞流动被抑制，液池右上角出现微小的逆时针小流胞。熔体内流函数最大值随Ma数增加而减小。由等温线图可知，随Ma数的增加，熔体最高温度和自由表面最高温度增加。晶体下方等温线保持水平，熔体几乎无流动。

图2 R-Z平面等流函数线和等温线图

图3给出了Q=1.53×10-2时，自由表面径向速度分布图和R=0.4处的径向速度在Z方向的分布图。

图3 自由表面径向速度分布和R=0.4处的径向速度沿Z向分布

Fig 3 Distribution of radial velocity along the free surface andZ

由图3可见，自由表面上的径向速度出现了3个极值。靠近晶体和坩埚壁的逆时针流胞使得自由表面形成了正极大值，而右侧顺时针流胞使得自由表面形成了负极大值。随着Ma数的增加，自由表面正向流动增强而负向流动减弱，说明熔体中逆时针流胞流动增强而顺时针流胞流动被抑制。从R=0.4处的径向速度分布图可见，随着Ma数的增大径向速度也增大。自由表面张力诱导的流动主要发生在0.1

2.1.2 热流密度Q对基本流的影响

底部热流加热和自由表面的辐射散热形成了贯穿液池的垂直方向的温度梯度，诱发了自下而上顺时针流动的右侧大流胞。图4给出了Ma=198时，液池内R-Z平面的等流函数线和等温线分布图。随着Q增大，熔体流动强度增强，右上角小流胞消失，坩埚内剩下两个反向旋转的流胞。底部和自由表面的最高温度逐渐坩埚壁移动。熔体中心等温线发生剧烈变化而晶体下部等温线保持水平。

当Ma=198时，垂直和水平温差在靠近晶体侧的驱动力方向一致，此处的径向速度达到了最大值，如图5所示。随着Q增加，左侧正向速度和右侧负向速度增加，右侧正向速度减小。这说明增大Q促进了左侧流胞和右侧大流胞的流动，抑制了右侧小流胞的流动。R=0.4处熔体流动为逆时针流动，自由表面温度梯度驱动的径向内流集中在0.1

2.2 流动转变

当底部热流密度和自由表面温度梯度不断增大直到超过一定值时，流场中任何一个微小的扰动都会不断地放大，使得流动状态从稳态变为非稳态。采用逼近法确定了流动转变的临界Mac数。如图6所示，增大Q可以使得流动转变的临界值减小，且较小的Q的改变可以造成较大临界Mac数变化。

图4 R-Z平面等流函数线和等温线图

图5 自由表面径向速度分布和R=0.4处的径向速度沿Z向分布

Fig 5 Distribution of radial velocity along the free surface andZ

图6 临界Mac数随Q的变化

2.3 三维振荡流动

当Ma数超过临界值后，熔体的流动转变为三维非稳态流动。此时硅熔体的流动较为复杂，为了更直观的了解熔体的周向速度的时相关特性，研究水平和垂直温度梯度对流动的影响，定义自由表面温度波动δT和自由表面速度波动δV为

(11)

(12)

2.3.1Ma数对振荡流的影响

由图7可见，随着Ma数的增大，自由表面的最大温度波动值不断增加。图8为Q=1.53×10-2，Ma=692时，一个周期内流动演变的过程。由图8可见，自由表面上速度波动呈波数为5的单或双层花瓣状振荡波，速度波动集中于晶体附近。振荡由外向内传递，为单、双层交替产生的结构。图9为R=0.35处的自由表面速度波动随时间变化的STD图，图中可见一簇明暗相间的直线且每条线从下往上由亮变暗，说明该点振荡在径向上有周期性的强弱变化，周向上没有运动。

图7 不同Q下的自由表面温度波动最大值随Ma数的变化

Fig 7 The max surface azimuthal temperature changes along the Ma at differentQ

图8 Ma=642, Q=1.53×10-2时，一个周期内表面速度波动随时间的变化

图9Ma=642时R=0.35处表面速度波动的STD图

Fig 9 The space-time diagram (STD) of surface azimuthal velocity along the circumference atR=0.35 forMa=642

图10给出了Q=1.53×10-2时不同Ma数下自由表面的速度波动图和STD图。当Ma=791时，表面波动转变为晶体附近振荡的波数为5的花瓣状热流体波。随着Ma数的进一步增大，振荡从晶体附近扩散到了整个熔体表面。当Ma=988时，晶体附近热流体波的流动区域被压缩，在热流体波外层出现了波数为7的振荡波，由STD图可见，外部振荡为三维稳态结构。随着Ma数增加到2 174，表面波动转变为波数为5的热流体波。从STD图可以看出，此时热流体波振幅呈周期性的变化。由此可见，自由表面振荡随Ma数的增加从晶体附近扩散到整个表面，随着Ma数增大，流动越来越不稳定。

2.3.2 热流密度Q对振荡流的影响

在液池底部所加的热流密度和表面散热产生了垂直方向的温度梯度，由图7可见，自由表面的最大温度波动值随Q的增加不断增加。

图11给出了Q=1.62×10-2和Ma=692时，自由表面速度波动和STD图。可以看出，随着Q的增大，热流体波波数和图10(a)相比减少到4个，波动集中在晶体附近，STD图由四对明暗相间的倾斜条纹组成。

图12给出了Q=1.62×10-2,Ma=1 383时的表面速度波动和STD图，在晶体附近存在波数为4的热流体波。其流动区域较图11明显减小，在热流体波外侧出现了7条直幅状振荡波。

图11Q=1.62×10-2,Ma=988,R=0.35表面速度波动图和STD图

Fig 11 Snapshots of surface azimuthal velocity and STD

由R=0.35处的STD图可以看出，晶体附近波动为热流体波，从R=0.75处的STD图可知，外围振荡波为三维稳态结构。与图10(b)对比可以发现，当流动转变为外部三维稳态而内部为热流体波的双层结构时，随着Q的增大，晶体附近的热流体波流动区域增大，流动强度增强。由图13可见，当Q较小而Ma数较大时，自由表面波动主要为三维稳态，而热流体波则被压缩到晶体附近区域几乎消失，当Ma数更大时，热流体波完全消失。

图12 Q=1.62×10-2, Ma=1 383表面速度波动图和STD图

图13Q=1.46×10-2,Ma=691时的表面速度波动图和STD图

Fig 13 Snapshots of surface azimuthal velocity fluctuation and STD

3 结 论

采用数值模拟的方法对双向温度梯度下Czochralski法生长硅晶体中的熔体热毛细对流进行了研究。分析了垂直和水平温差对熔体流动的影响，确定了流动转变的临界值。结果表明：

(1) 当Ma数和Q较小时，流动为稳态。随Ma数的增加和Q的减小，熔体右上角出现一个微小的流胞，晶体下部熔体几乎没有流动。此时的熔体流动Q起主导作用，右上角小流胞和右侧大流胞相互抑制，增大Ma数和减小Q可使得熔体整体流动减弱，流动更稳定；

(2) 随着Ma数的增大，流动转变为非稳态。临界Mac数随Q的增大而减小，且Q微小的改变能造成临界Mac数的显著改变。硅晶体生长过程中使用较小的Q可以延缓流动失稳现象。

(3) 当流动失稳转变为非稳态后，Ma数为改变自由表面波形的关键因素。随着Ma数的增加，自由表面波形由单、双层花瓣互相转换的振荡波转变为花瓣状热流体波，接着转变为外层直幅波和内层热流体波同时存在的结构并最终转变为弯曲的条幅状热流体波，随着Ma数的增大熔体自由表面波动不断增强；

(4) 流动失稳后，随着Q的增大，热流体波波数减小，熔体自由表面波动不断增强。当Q相对于Ma数较小时，靠近晶体侧热流体波消失，晶体附近流动较稳定；而增大Q，晶体附近速度波动增加，选用较大的Ma数和较小的Q有利于增加晶体附近流体流动的稳定性。

综上所述，底部热流Q对熔体内Marangoni-热毛细对流的稳定性有着极为重要的影响，Q过大容易导致流动失稳并且会造成结晶界面附近剧烈振荡，影响晶体质量。而选择较大的Ma数可以抑制结晶界面附近的振荡。因此在晶体生长过程中可以选用较小的Q搭配较大的Ma数来减弱结晶界面周围的流体振荡，提高晶体质量。

[1] Kumar V, Biswas G, Brenner G, et al. Effect of thermocapillary convection in an industrial Czochralski crucible: numerical simulation [J]. International Journal of Heat and Mass Transfer, 2003, 46(9):1641-1652.

[2] Anilkumar A V, Grugel R N, Bhowmick J, et al. Suppression of thermocapillary oscillations in sodium nitrate floating half-zones by high-frequency end-wall vibrations[J]. Journal of Crystal Growth, 2004, 276(s1-2):194-203.

[3] Teitel M, Schwabe D, Gelfgat A Y. Experimental and computational study of flow instabilities in a model of Czochralski growth [J]. Journal of Crystal Growth, 2008, 310(7-9):1343-1348.

[4] Hintz P, Schwabe D, Wilke H. Convection in a Czochralski crucible-part1: non-rotating crystal [J]. Journal of Crystal Growth, 2001, 222(1-2):343-355.

[5] Schwabe D. Buoyant-thermocapillary and pure thermocapillary convective instabilities in Czochralski systems [J]. Journal of Crystal Growth, 2002, 237-239:1849-1853.

[6] Yi K W, Kakimoto K, Eguchi M, et al. Spoke patterns on molten silicon in Czochralski system[J]. Journal of Crystal Growth, 1994, 144(1): 20-28.

[7] Nepomnyashchy A A, Simanovskii I B, Braverman L M. Stability of thermocapillary flows with inclined temperature gradient[J]. Journal of Fluid Mechanics, 2001, 442: 141-155.

[8] Jing C J, Tsukada T, Hozawa M, et al. Numerical studies of wave pattern in an oxide melt in the Czochralski crystal growth[J]. Journal of Crystal Growth, 2004, 265(265):505-517.

[9] Yao L, Zeng Z, Li X, et al. Effects of rotating magnetic fields on thermocapillary flow in a floating half-zone[J]. Journal of Crystal Growth, 2011, 316(1):177-184.

[10] Yao L, Zeng Z, Chen J, et al. Investigation of convection control under the non-uniform RMF in a liquid bridge[J]. Procedia Engineering, 2012, 31(4):659-664.

[11] Peng Z, Li D, Qi K. Transition to chaos in thermocapillary convection[J]. International Journal of Heat & Mass Transfer, 2013, 57(2):457-464.

[12] Takagi Y, Okano Y, Minakuchi H, et al. Combined effect of crucible rotation and magnetic field on hydrothermal wave[J]. Journal of Crystal Growth, 2014, 385(1):72-76.

[13] Yamamoto T, Takagi Y, Okano Y. Numerical investigation of the effect of free surface shape on the direction of thermocapillary flow in a thin circular pool[J]. Journal of Chemical Engineering of Japan, 2015, 48(6):407-417.

[14] Wang F, Peng L, Zhang Q Z, et al. Effect of the vertical heat transfer on the thermocapillary convection in a shallow annular pool[J]. Microgravity Science & Technology, 2015, 27(2):107-114.

[15] Li Y R, Imaishi N, Azami T, et al. Three-dimensional oscillatory flow in a thin annular pool of silicon melt[J]. Journal of Crystal Growth, 2004, 260(1):28-42.

Thermocapillary convection in Czochralski silicon growth by bidirectional temperature gradients under microgravity

WEI Chengxingyun，PENG Lan, ZHANG Quanzhuang

(Key Laboratory of Low-Energy Utilization Technologies and Systems of Ministry of Education, College of Power Engineering, Chongqing University, Chongqing 400044,China)

The bidirectional temperature gradients play an important part in the convection of crystal growth. However, most of the researches before only focused on unidirectional temperature. In this paper, under microgravity, a serious of numerical simulations was conducted to study the thermocapillary convection in Czochralski growth of silicon crystal. The coupling effects of vertical and horizontal temperature gradients were discussed. The radiation on the melt surface was considered, the range of horizontal and vertical temperature gradient wereMa=(0-3000) andQ=(1.39×10-2-1.76×10-2) respectively. Results show that flow is steady for smallQandMa. In this case, there are three flow cells in the melt, the melt flow is dominated byQ; the flow is more stable due to the decrease of theQand the increase of theMa. When the Ma exceeds a threshold value, an unsteady three dimensional flow is developed. With the increase of theQ, the critical Ma significantly decreased. When the flow is unsteady, a new way of the flow pattern transtion is found.Mais the key for the change of the surface fluctuation pattern. The number of the hydrothermal wave is changed byQ, and the generation of hydrothermal wave which is near the crystal is determined byQ. With the enhancement of theQandMa, the flow pattern enventually changes into curved spoke patterns.

thermocapillary convection; Cz configuation; bidirectional temperature gradients; numerical simulation; surface tension

1001-9731(2016)12-12090-07

国家自然科学基金资助项目(51276203)

2016-01-04

2016-03-15 通讯作者：彭 岚，E-mail：penglan@cqu.edu.cn

魏程星云 (1991-)，男，武汉人，在读硕士，师承彭岚教授，从事工程热物理、热毛细对流相关研究。

TK124

A

10.3969/j.issn.1001-9731.2016.12.014