基于主成分判别分析的高光谱遥感影像分类方法

陈 庆，黄 蕾，李雪梅

（1.湖北省测绘工程院，湖北 武汉 430074；2.湖北省基础地理信息中心，湖北 武汉 430074；3.湖北省航测遥感院，湖北 武汉 430074）

基于主成分判别分析的高光谱遥感影像分类方法

陈 庆1，黄 蕾2，李雪梅3

（1.湖北省测绘工程院，湖北 武汉 430074；2.湖北省基础地理信息中心，湖北 武汉 430074；3.湖北省航测遥感院，湖北 武汉 430074）

提出了一种基于主成分判别分析的高光谱遥感影像分类方法。针对高光谱遥感影像数据量大、冗余信息多的特点，使用改进的线性判别分析方法对高光谱遥感数据进行线性维数减少。该方法将主成分分析加入到线性判别分析的算法框架中，能够克服常规的线性判别分析方法在训练样本数量较少时遭遇到的小样本问题。通过实验，证明基于主成分判别分析的遥感影像分类方法能够利用少量的训练样本实现更优的分类精度。

主成分分析；线性判别分析；高光谱；分类

现代化观测技术的快速发展，对遥感信息处理速度和质量提出了更高要求[1]。高光谱遥感能够在紫外到红外波长区的范围内提供细致丰富的地物光谱特征描述，提高了遥感影像对地物的分类识别能力[2,3]。然而，随着实际应用中对遥感影像自动化处理程度要求的提高，高光谱遥感影像在提供多波段、高量化级数的遥感影像同时，也给计算机自动数据处理带来了新的挑战[4,5]。为了充分利用高光谱的信息同时减少因数据冗余带来的复杂计算，必须首先对高光谱数据进行维数减少，以更加有效的低维空间来表达原始高维特征空间中的样本分布，降低数据量的同时提高分类的精度[6]。

国际上针对减少高光谱遥感影像的数据维数已经进行了一系列的研究。例如以主成分分析（PCA）[7]为代表的非监督特征提取方法采用线性变换的方法，将原始高维特征空间中的主成分信息组合到新的特征空间中，该类方法计算简单，不需要先验知识，因此被广泛应用于高光谱遥感影像降维[8]。此外，线性判别分析（LDA）[9]作为一种监督的判别分析方法，能够充分考虑训练样本的判别信息以提高样本在输出低维特征空间中的可分性，已经被证明是一种更有效的特征提取方法。然而，该方法在训练样本数量较少时会遭遇小样本问题[10,11]，无法找到最优的低维特征子空间，在大多数遥感影像分类问题中不能保证足够的分类精度，限制了线性判别分析方法在遥感影像智能化处理中的应用。本文致力于解决上述问题，引入改进的线性判别分析方法对高光谱遥感数据进行线性维数减少。

1 主成分判别分析

本文提出的基于主成分判别分析的高光谱遥感影像分类方法主要步骤如下：为解决小样本问题，主成分判别分析对原始输入的数据进行两次线性投影变换。首先采用主成分分析降低输入特征的维数，将原始光谱特征空间转化为最佳的特征描述空间，然后采用线性判别分析方法进一步降低特征维数，将特征从前一步最佳的特征描述空间转化为最佳的特征判别空间。然后在特征判别空间中，采用最简单的最小距离分类器对遥感影像中的每个像素类别进行分类。

i是原始光谱特征维数；N为训练样本数目。训练样本的协方差矩阵Φ表示为：

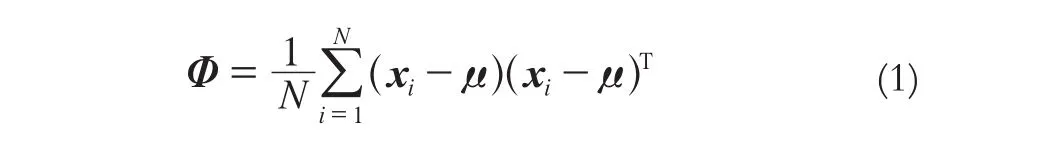
求解特征方程：

最大的M个非零特征值λ1≥λ2≥…≥λM所对应的特征向量集组成了原始训练样本集的最佳的特征描述空间，即

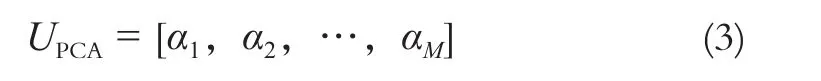
最佳的特征描述空间的维数M的选取原则除了与特征方程的特征值数量有关，还与线性判别分析中的训练样本的类别数及其类间散布矩阵的秩有关。

其中，μ'i和μ'分别是第i类的训练样本和全部训练样本在最佳特征描述空间中的均值向量。为了使样本在最终的特征判别空间中同类的样本尽可能集中分布，不同类的样本尽可能分散分布，最佳的特征判别空ULDA应该满足如下准则：

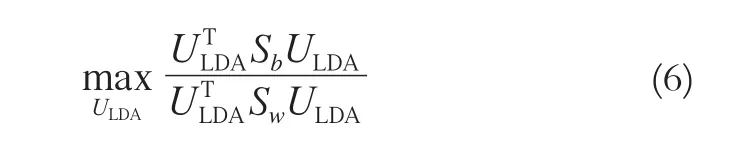
式（6）是矩阵分析中著名的Rayleigh商[12,13]，使得式（6）达到最大值的ULDA是广义特征值问题式（7）中对应D个最大特征值的特征向量集：

对于式（7），如果Sw非奇异，则可以转化为一般特征值问题：

在常规的线性判别分析算法中，根据类内散布矩阵的定义有Rank（Sw）≤N-C，而类内散布矩阵的维数Dim（Sw）=L。当Rank（Sw）＜Dim（Sw）时，矩阵Sw是奇异矩阵，广义特征值问题不可解，这就是机器学习方法中常见的小样本问题。在高光谱遥感影像分类问题中，由于训练样本数量常常远小于光谱特征维数，因此，直接使用常规的线性判别分析算法必然会遭遇到上述小样本问题。采用本文提出的主成分判别分析算法后，通过在主成分分析中对特征描述空间的维数M的设置，约束该特征空间的维数使其不大于Rank（Sw），可以满足在该特征空间中的矩阵Sw是满秩矩阵，即可克服常规的线性判别分析方法在训练样本数量较少时遭遇到的小样本问题。此外，还需保证该子空间的维数不小于类别数C。主成分分析中对特征描述空间的维数M的设置条件如下：

分别得到主成分判别分析的两次线性投影变换矩阵UPCA和ULDA以后，原始光谱特征空间转化为最佳的特征判别空间的线性投影矩阵为：

2 实验与分析

为了验证本文提出的方法的有效性，采用华盛顿DC地区的HYDICE高光谱影像数据子集进行分类实验[14,15]。该影像由普度大学提供，影像大小为307×1 280像素，本文实验中选取其中307×250大小的子区域。该影像数据在光谱范围0．4～2．4 μm的可见光和近红外区域内收集了210个波段的高光谱数据，去除了吸水性的波段后，剩余的191个波段的影像数据用于实验。实验影像如图1a所示，影像中包含的主要地物类型是水体、房屋、道路、小路、草地、树木和阴影。该高光谱影像数据分类的主要难点在于其地物类别的复杂性和主要地物类型光谱的相似性[16]。

图1 HYDICE高光谱影像数据及其参考数据

实验分别选用原始光谱特征、主成分分析的特征、线性判别分析的特征和本文提出的主成分判别分析的特征作为输入特征，采用最简单的最小距离分类器对遥感影像中的每个像素类别进行分类。其中参考数据如图1b所示，实验中训练样本从参考数据中随机产生，数量为每类地物20像素，用于统计分类精度的测试样本即为全部参考数据。对于3种特征维数减少方法，首先将输出的特征维数固定为10。

分类结果如图2所示，从分类结果可知，主成分判别分析方法效果最优。原始光谱特征分类和主成分分析的分类结果非常接近，这是由于主成分分析的特征提取方法将原始特征投影到方差最大的低维子空间，因此使用最小距离分类器会得到与原始特征相近的分类结果。通过这两种特征的分类结果图可以看出，影像左上方的屋顶被大量错分为小路，此外，在分类结果图的道路中出现了错分的水体，本文提出的主成分判别分析方法完全避免了这些误分类的情况。进一步比较图2c和d可知，虽然在维数减少的过程中，常规的线性判别分析方法同样使用了训练样本的判别信息，但是该方法效果并不理想，原因是在线性判别分析中输入的训练样本数量（20×7=140）小于原始光谱特征维数（191），线性判别分析方法出现了小样本问题，特征提取过程中出现了较大的误差，导致分类过程出现错误。

图2 HYDICE高光谱影像数据分类结果图

图3为3种方法的提取特征维数与分类精度的关系图，分别表示分类总体精度和分类Kappa系数随着特征维数的增加而变化的情况。从图3可以看出，当特征维数小于5时，3种维数减少方法的分类精度随特征维数的增加呈明显上升趋势；当特征维数接近7时，3种方法的分类精度都达到顶点；当特征维数进一步增大时，分类精度变化十分缓慢，略微下降后基本接近平缓，保持不变。最优的特征维数是接近影像中的地物类别数C，在本实验中，C=7。本文提出的方法在分类精度曲线上始终明显地处于最优的位置，此外，分类总体精度和分类Kappa系数随数据特征维数增加的变化趋势基本一致。

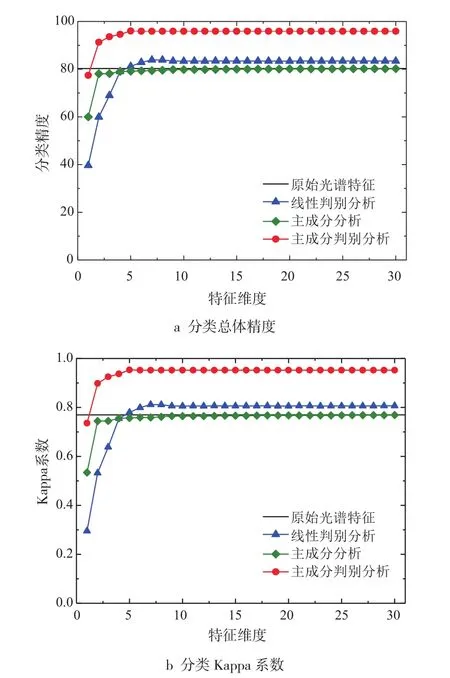
图3 HYDICE高光谱影像数据特征维数与分类精度的关系

本文提出的方法与3种对比方法对HYDICE高光谱影像数据分类精度定量统计结果如表1所示。从表1可以看出，本文提出的方法在各种地物的单类分类精度和分类总体精度都取得了最优效果，其中对于该影像中的难点，房屋、道路和小路的分类均取得了非常好的效果，而对比方法在道路的分类结果上均出现了较大的误分类，使得道路的分类精度较低。由于训练样本数量不足，常规的线性判别分析方法的分类精度低于直接使用原始光谱特征的分类精度，而本文提出的方法能够在少量训练样本的情况下将高光谱遥感影像的分类精度从80．26%提高到95．92%。

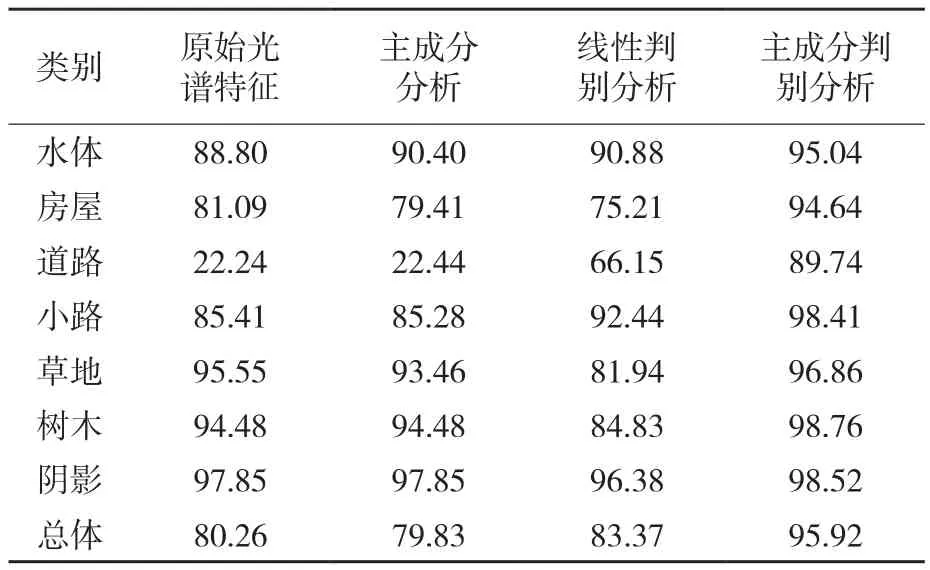
表1 HYDICE高光谱影像数据分类精度定量统计/%

3 结 语

本文提出了一种基于主成分判别分析的高光谱遥感影像分类方法。针对常规的线性判别分析方法直接用于对高光谱遥感数据进行线性维数减少时出现的小样本问题，将主成分分析加入到线性判别分析的算法框架中，通过两次线性投影变换的策略，在主成分分析得到的最佳特征描述空间进行线性判别分析进一步降低特征维数，将特征从最佳特征描述空间转化为最佳特征判别空间。由于对最佳特征描述空间的维数进行了约束，该特征空间的维数不大于类内散布矩阵的秩，可以满足在该特征空间中进行线性判别分析的类内散布矩阵是满秩矩阵，克服了常规的线性判别分析方法在训练样本数量较少时遭遇到的小样本问题。通过与原始光谱特征、主成分分析的特征、线性判别分析的特征对比，基于主成分判别分析的遥感影像分类方法能够利用少量训练样本实现更优的分类精度。

[1] Plaza A,Plaza J,Paz A,et al．Parallel Hyperspectral Image and Signal Processing[J]．IEEE Signal Processing Magazine,2011(28)∶119-126

[2] 张乐飞．遥感影像的张量表达与流形学习方法研究[J]．测绘学报,2013(5)∶790

[3] Landgrebe D．Signal Theory Methods in Multispectral Remote Sensing[M]．New Jersey∶Wiley,2003

[4] 陶超,邹峥嵘,丁晓利,等．利用角点进行高分辨率遥感影像居民地检测方法[J]．测绘学报,2014(2)∶164-169

[5] Kwon H,Nasrabadi N M．Kernel Matched Subspace Detectors for Hyperspectral Target Detection[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006(28)∶178-194

[6] Jimenez L O,Landgrebe D A．Hyperspectral Data Analysis and Supervised Feature Reduction Via Projection Pursuit[J]．IEEE Transactions on Geoscience and Remote Sensing,1999(37)∶2 653-2 667

[7] Jolliffe I T． Principal Component Analysis[M]．New York∶Springer,2002

[8] Michael J, Farrell D,Mersereau R M．On the Impact of PCA Dimension Reduction for Hyperspectral Detection of Difficult Targets[J]．IEEE Geoscience and Remote Sensing Letters,2005(2)∶192-195

[9] 徐尽．基于线性判别分析的数据集可分性判定算法[J]．科技通报,2013,29(4)∶31-32

[10] Neumaier A．Solving Ill-conditioned and Singular Linear Systems∶a Tutorial on Regularization[J]．SIAM Review,1998(40)∶636-666

[11] 赵越,徐鑫,乔利强,等．张量线性判别分析算法研究[J]．计算机技术与发展,2014(1)∶73-76

[12] Bhatia R． Matrix Analysis[M]．New York∶ Springer-Verlag,1997

[13] Boyd S, Vandenberghe L． Convex Optimization∶ Cambridge Univ[M]．Cambridge∶Cambridge Univ．Press,2004

[14] Landgrebe D．Hyperspectral Image Data Analysis[J]． IEEE Signal Processing Magazine,2002(19)∶17-28

[15] Benediktsson J A,Palmason J A,Sveinsson J R．Classification of Hyperspectral Data from Urban Areas Based on Extended Morphological Profiles[J]． IEEE Transactions on Geoscience and Remote Sensing,2005(43)∶480-491

[16] Huang X,Zhang L．An Adaptive Mean-Shift Analysis Approach for Object Extraction and Classification from Urban Hyperspectra l Imagery[J]．IEEE Transactions on Geoscience and Remote Sensing, 2008(46)∶4 173-4 185

P237

B

1672-4623（2016）01-0076-03

10.3969/j.issn.1672-4623.2016.01.022

陈庆，硕士，工程师，主要研究方向为3S技术应用。

2014-11-04。

项目来源：国家自然科学基金资助项目（91338202）。