“传感器技术”和“信号与系统”课程的交叉教学
任 蕾, 林鑫伟
(上海海事大学 信息工程学院, 上海 201306)
“传感器技术”和“信号与系统”课程的交叉教学
任 蕾, 林鑫伟
(上海海事大学 信息工程学院, 上海 201306)
“传感器技术”是一门多学科交叉课程,教学内容涉及众多领域。传感器是一类特定的系统,可应用“信号与系统”课程中的系统分析理论研究其特性,两门课程扮演的角色分别是应用和方法论,相互支撑。本文介绍了这两门课程的交叉知识点、传感器动态特性分析的基本方法,并利用两个应用实例,阐述应用线性系统分析方法求解传感器动态性能的过程。
交叉教学;系统分析;传感器动态性能
0 引言
“传感器技术”课程内容涉及很广,包括:电子线路、信号与系统、物理学、机械、材料科学、微电子学等。且该领域技术更新快,教学内容较杂散,教与学的难度很大。国内在传感器课程改革上已开展了许多积极探索并获得丰富的教学成果[1-6]。
“信号与系统”课程教授的是方法论,涉及线性时不变系统分析的基本方法和理论,而工程中遇到的各类实际系统可在特定条件下,应用该理论解决。在文献[1]中指出“信号与系统”课程改革的重要方向之一是加强与工程实例的结合。
笔者同时教授这两门课程,发现两者之间可以相互支撑,本文以传感器动态性能的教学内容为例,介绍两门课程之间的交叉知识点的教学方法,同时给出两个实例。
1 两门课程的交叉教学
1.1 交叉知识点
笔者在教授“信号与系统”与“传感器技术”两门课程中,发现“信号与系统”分析的基本理论是分析传感器动态特性的基础,而讲授系统分析理论时,需要配以工程应用实例加深学生对知识点的理解,在此过程中,可以将两者有机结合。图1阐述了两门课程的交叉教学点。

图1 “信号与系统”、“传感器技术”交叉教学点
由于传感器的惯性和滞后等原因,传感器的输出需经过一段时间才能稳定,因此分析其动态特性是必要的。而目前最常用的传感器数学模型是线性常系数微分方程,根据信号与系统分析理论,在传感器等效为线性时不变系统的前提下,可由线性系统时域和变换域两类分析方法解决。上述可归结为:工程应用(Engineering)—建模(Modeling)—分析(Analysis)的三步过程。“信号与系统”课程提供传感器动态模型的建模方法和分析手段,而传感器技术是一类特定系统,为前者提供课程教学的应用实例,两者相互支撑。
1.2 传感器动态特性的数学模型
传感器的动态特性数学模型一般由下述常系数线性微分方程描述[8-9]:
(1)
式中,x(t)是传感器的输入,即待测量,y(t)是传感器的输出,微分方程的系数由传感器特性决定。最常见传感器可分别由零阶系统、一阶系统、二阶系统描述,即:
a0y(t)=b0x(t)
(2)
(3)
(4)
工程应用中,电位器式的电阻传感器、变面积式的电容传感器、利用静态式压力传感器测量液位均可看作零阶系统[9]。常见一阶传感器系统包括:不带套管热电偶测温系统、电路中常用的阻容滤波器、弹簧—阻尼系统、液体温度计等[8-9]。而振动系统、压力传感器、加速度传感器、带有套管的热电偶、电磁式的动圈仪表等可建模为二阶系统。
1.3 传感器动态特性的分析方法
对传感器的动态特性建模后,可选择系统分析的时域方法和变换域方法,而常用方法是利用傅里叶变换和拉普拉斯变换,分别从系统频率响应和系统函数的角度出发,得到传感器的动态特性。
式(3)表示的一阶系统数学模型可以写成:
(5)
其中τ是系统时间常数,k是传感器的静态灵敏度,因此一阶传感器系统的系统函数为
H(s)=k/(1+τs)
(6)
对应的频率特性为
H(jω)=k/(1+τjω)
(7)
该一阶传感器系统呈现一阶低通滤波的特性,当时间常数τ越小时,传感器系统的频率响应特性越好。从系统分析的角度阐述,即低通滤波器的截止频率越大,通带越宽,其频率响应越好;系统时间常数越小,说明系统响应时间越短,系统的响应能快速跟上激励的变化。
式(4)表示的二阶系统数学模型可写为
(8)
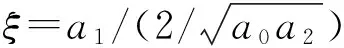
该传感器系统的系统函数为
(9)
系统的频率响应为
(10)
根据系统分析理论可知,二阶传感器系统的特性取决于阻尼系数的取值,取值不同时,系统呈现出无阻尼、过阻尼、临界阻尼和欠阻尼四类情况,其实质是二阶系统的极点分布决定了系统频率响应,这一知识点在“信号与系统”课程的复频域系统分析中有具体讲解。
2 实例分析
2.1 实例1
已知某一阶传感器的系统函数为
H(s)=1/(τs+1),τ=0.001(s)
试求该传感器输入信号工作频率范围[9]。
根据系统函数得,该一阶传感器的频率响应为
H(jω)=1/(jωτ+1)
幅频响应为
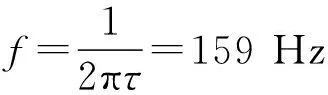
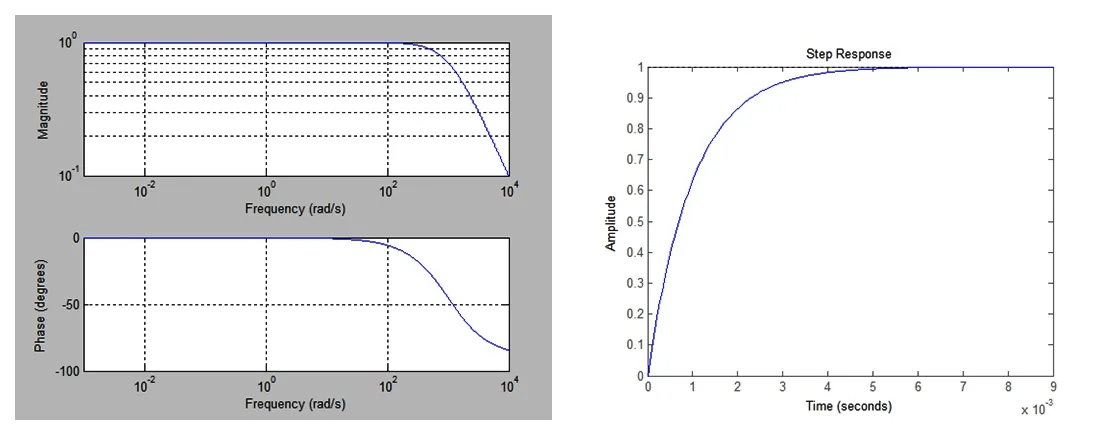
(a)频率特性 (b) 阶跃响应图2 一阶传感器特性
2.2 实例2
某压电式加速度计动态特性为
式中,q为输出电荷量(pC);a为输入加速度(m/s2)。确定该加速度计的静态灵敏度系数、固有频率和阻尼系数。当阶跃信号作为激励信号时,该传感器响应是什么[9]?

利用复频域分析方法得该传感器系统阶跃响应的拉普拉斯变换为
逆变换后求解系统阶跃响应波形如图3(a)所示,该系统的幅频特性和相频特性如图3(b)所示。

(a) 阶跃响应波形 (b) 频率响应图3 二阶传感器响应曲线
由上可见,该实例传感器的阶跃响应是一个振荡衰减信号,系统处于欠阻尼状态。
上述两个实例可作为“信号与系统”课程频域分析的实例,同时也是“传感器技术”课程的动态性能分析的教学知识点,因此可以相互支撑有机结合起来。
3 结语
目前,与工程结合、多学科交叉的教学方法是工科本科专业的教学改革方向之一。“传感器技术”课程中动态特性分析的理论基础是“信号与系统”课程的系统分析方法,在实例分析中,将两者有机结合,可帮助学生掌握整个教学体系中不同课程的关联性。
[1] 郑君里,谷源涛. 试谈“信号与系统”课程理论与实践之结合[J]. 南京:电气电子教学学报,2014,36(3):1-5
[2] 杨鹏. “传感器原理及应用”课程双语教学研究[J]. 南京:电气电子教学学报,2008,30(1):110-111
[3] 徐科军. 信号检测、处理及实验系列课程建设探讨[J]. 南京:电气电子教学学报,2009,31(2),11-12,24
[4] 王海欣,徐科军. 一种信号检测与处理综合实验平台的研制[J]. 南京:电气电子教学学报,2010,32(2):67-69,76
[5] 苑慧娟,秦勇,周真,王雁. “传感技术”课程设计改革探索[J]. 南京:电气电子教学学报. 2010,32(4),91-92
[6] 刘剑,杨立才,刘常春. “生物医学传感器与测量”课程教学改革探索[J]. 南京:电气电子教学学报. 2011,33(1),15-16
[7] 闻福三,赵京明,王玲玲. 霍尔效应和霍尔传感器的教学方法研究[J]. 南京:电气电子教学学报. 2012,34(2),118-120
[8] 樊尚春. 传感器技术及应用[M]. 北京:北京航空航天大学出版社. 2010年10月
[9] 王化祥,张淑英. 传感器原理及应用[M]. 天津:天津大学出版社. 2007年2月
Discussion about Cross Teaching of Two Courses
REN Lei, LIN Xin-wei
(CollegeofInformationEngineering,ShanghaiMaritimeUniversity,Shanghai201306,China)
Sensor Technology is a multidisciplinary course. The teaching contents deal with many domains. Senor is a certain system, for which system analysis method introduced in Signal and System course can be applied for studying the characteristics. Therefore, the roles of two courses are application and methodology respectively, which supports for each other. Cross teaching contents and fundamental method for analyzing dynamic characteristics of sensor are introduced. Two application examples are presented to illustrate the analysis process of dynamic characteristics for sensor using linear system analysis theory.
cross teaching; system analysis theory; dynamic characteristics of sensor
2015-07-06;
2015-11- 10
上海海事大学2015年度校级重点课程建设项目
任 蕾(1979-),女,博士, 讲师,主要从事通信与信息类课程教学与研究工作,E-mail:leiren@shmtu.edu.cn
G642.0
A
1008-0686(2016)02-0018-03

