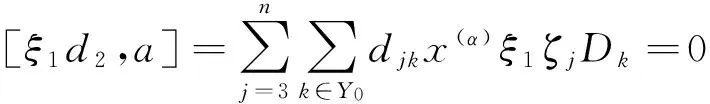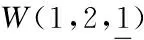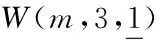素特征域上gl(0，2)在广义Witt李超代数中的中心化子

郑克礼，张永正

(1.东北林业大学理学院数学系，黑龙江 哈尔滨 150040；2.东北师范大学数学与统计学院，吉林 长春 130024)

素特征域上gl(0，2)在广义Witt李超代数中的中心化子

郑克礼1，张永正2

(1.东北林业大学理学院数学系，黑龙江 哈尔滨 150040；2.东北师范大学数学与统计学院，吉林 长春 130024)

主要研究素特征域上gl(0，2)在广义Witt李超代数中的中心化子，其中gl(0，2)是一般线性李超代数的子代数.首先，考虑了广义Witt模李超代数作为gl(0，2)模的分解；接下来，计算了从gl(0，2)到广义Witt李超代数的每个子模的内导子；最后，用解线性方程组的方法完全确定了gl(0，2)在广义Witt李超代数中的中心化子.

中心化子；李超代数；模；上同调群

0 引言

中心化子的概念起源于群结构的研究.[1]作为李(超)群的线性化对象，李(超)代数自然也存在着中心化子[2-3]，即：若S为李(超)代数L的子集，则称

CL(S)={x∈L|[x，s]=0，∀s∈S}

为S在L中的中心化子.

显然中心化子不仅仅是一个子集，还是一个子代数.因为对于伴随表示一个李(超)代数可以作为其子代数的自然模，则上面中心化子的概念等价于系数在L上的S的零维上同调群.又由于代数的零维上同调群可归结为内导子的研究，所以了解李(超)代数导子的结构就显得尤为重要.早在1970年，俄国数学家Celousov就对Cartan型模李代数的导子代数进行了的研究.[4]Skryabin在文献[5]中给出了模李代数导子的更一般结论.近年来Cartan型模李超代数内外导子也被大量的研究，[6-8]进而推动了Cartan型模李超模代数的零维上同调群发展.文献[9]对系数在Witt和特殊超代数上的单模李超代数A(1；0)的低维上同调进行了深入研究，给出了解决此类问题的同调方法.本文的原始思想来源于文献[10-11].虽然在文献[11-12]中分别决定了系数在广义Witt李超代数的两类特殊子模上gl(0，2)的零维和一维上同调群，但对于广义Witt李超代数的一般情况是未知的.本文将给出一些结论，并且为研究一般线性李超代数在更复杂模中的中心化子结构提供理论基础.

1 预备知识

令L是素特征域上的李代数且V是任意的L-模.

线性映射ψa：L→V，如果存在a∈V使得对于x∈L有ψa(x)=x·a，则称ψa为由L到V的内导子.记Ider(L，V)为所有由L到V的内导子的集合，由上同调群的定义可得零维上同调群H0(L，V)={a∈V|x·a=0，x∈L}[13].综合内导子和零维上同调群的定义，

Ider(L，V)=H0(L，V).

本文将素特征域上的广义Witt李超代数[14]的写法做如下调整：

依然记Y0∶={1，2，…，m}，但记Y1∶={1，2，…，n}，于是

Bk∶={〈i1,i2,…,ik〉|1≤i1

令D1，…，Dm，d1，…，dn是O上的线性变换并且εi∶=(δi1，…，δim)，使得：

Di(x(α)ξu)=x(α-εi)ξu，i∈Y0；

dj(x(α)ξu)=(-1)u(j)x(α)ξu-〈j〉，j∈Y1.

其中δij是Kronecker符号.再令

则称W为素特征域上的广义Witt李超代数，且其包含在Der(O)中.显然W拥有一组基

{x(α)ξuDi，x(α)ξudj|α∈A，u∈B，i∈Y0，j∈Y1}.

由基的结构知

其中

显然{eij|i，j=1，2}是gl(0，2)的标准基，其中eij是(i,j)位置为1、其他位置为0的矩阵.由于gl(0，2)是李代数，可以证明gl(0，2)同构于W的子代数〈ξidj|i,j=1,2〉，则W可通过伴随表示看作gl(0，2)-模.又由中心化子的概念，可得在此情况下

CW(gl(0,2))=H0(gl(0,2),W).

即：要得到中心化子CW(gl(0,2))，只需要计算出零维上同调群H0(gl(0,2)，W).

如不另行说明，在本文中u为B中元素，{ξidj|i,j=1,2}为gl(0,2)的标准基.由文献[13]可知

其中

2 素特征域上的CW(gl(0，2))

为了决定素特征域上的CW(gl(0,2))，只需要对所有的i=0，…，n，分别处理H0(gl(0,2)，Wi)与H0(gl(0,2)，Wi)即可.首先，将考虑零维上同调H0(gl(0,2)，W).

命题2.1H0(gl(0,2)，W0)=〈x(α)Dk|k∈Y0〉.

证明 由定义有W0=〈x(α)Dk|k∈Y0〉.对任意x∈gl(0,2)，有[x,x(α)Dk]=0，则

H0(gl(0,2)，W0)=W0=〈x(α)Dk|k∈Y0〉.

命题2.2H0(gl(0,2)，W1)=〈x(α)ξiDk|i∈Y1{1，2}，k∈Y0〉.

证明 根据Wi的定义，W1=〈x(α)ξiDk|i∈Y1，k∈Y0〉.设存在

其中Cik∈F，满足[gl(0,2),a]=0.则：

已知D1，D2，…，Dm是线性无关的，则C1k=C2k=0.这意味着对所有的y∈gl(0,2)，i∈Y1{1,2}与k∈Y0有[y,x(α)ξiDk]=0.因此结论成立.

命题2.3H0(gl(0,2)，W2)=〈x(α)ξu-〈1〉-〈2〉Dk||u|=4，k∈Y0〉.

证明 对y∈gl(0,2)，|v|=4与k∈Y0，显然有[y,x(α)ξv-〈1〉-〈2〉Dk]=0.现在只需考虑〈x(α)ξ1ξiDk〉与〈x(α)ξ2ξjDk〉，其中i∈Y1{1}，j∈Y1{1,2}.设存在W2=〈x(α)ξuDk||u|=2，k∈Y0〉中的元素

使得[gl(0,2),a]=0，其中cik，djk∈F.则：

应用命题2.2的方法，对于i∈Y1{1}，j∈Y1{1,2}，k∈Y0，有cik=djk=0.因此就证明了结论H0(gl(0,2),W2)=〈x(α)ξu-〈1〉-〈2〉Dk||u|=4，k∈Y0〉.

类似于命题2.3的证明，可以给出如下推论和命题：

推论2.1H0(gl(0,2),Wi)=〈x(α)ξu-〈1〉-〈2〉Dk||u|=i+2，k∈Y0，0≤i

命题2.4H0(gl(0,2)，Wn-1)=0.

命题2.5H0(gl(0,2)，Wn)=0.

综合以上结论有下面结论成立：

其次，对所有i=0，1，…，n，下面考虑零维上同调H0(gl(0,2)，Wi).

命题2.6H0(gl(0,2),W0)=〈x(α)dl|l∈Y1{1,2}〉.

[ξ1d2，a]=-C1x(α)d2=0；[ξ2d1，a]=-C2x(α)d1=0；

[ξ1d1，a]=-C1x(α)d1=0；[ξ2d2，a]=-C2x(α)d2=0.

由x(α)d1≠0与x(α)d2≠0得到C1和C2都为零.

应用类似的方法，可以得到下面命题：

命题2.8

〈x(α)ξu-〈1〉-〈2〉dl||u|=4，l∈Y1{1，2}〉.

推论2.2 对于1≤i

〈x(α)ξu-〈1〉-〈2〉dl||u|=i+2，l∈Y1{1，2}〉.

命题2.9H0(gl(0,2),Wn-1)=〈x(α)(ξE-〈1〉d2+ξE-〈2〉)d1〉.

命题2.10H0(gl(0,2),W2)=0.

由以上结论可得下面定理.

定理2.2

综合定理2.1与定理2.2易得以下结论.

定理2.3

[1] JACOBSON N.Basic algebra I[M].2nd ed.New York：Dover Publications，2009：41-42.

[2] JACOBSON N.Lie algebras[M].New York：Interscience Publishers，1962：27-28.

[3] SCHEUNERT M.Theory of Lie superalgebras.An introduction[M].New York：Springer-Verlag，1979：6-12.

[4] CELOUSOV M J.Dervation of Lie algebras of Cartan-type[J].Izv Vyssh Uchebn Zaved Mat，1970，98：126-134.

[5] SKRYABIN S M.Isomorphisms and derivations of modular Lie algebras of Cartan type[J].Russ Math Surv，1987，42：245-256.

[6] BAI W，LIU W D.Superderivations for modular graded Lie superalgebras of Cartan type[J].Algebr Represent Theor，2014，17：69-86.

[7] 马丽丽，张朝凤，张永正.有限维模李超代数U的导子超代数[J].东北师大学报(自然科学版)，2011，43(2)：1-6.

[8] 李明，徐晓宁.无限维模李超代数Ω的超导子代数[J].东北师大学报(自然科学版)，2014，46(3)：7-11.

[9] LIU W D，SUN L P.Low-dimensional cohomology of Lie superalgebraA(1；0) with coefficients in Witt or special superalgebras[J].Taiwanese J Math，2013，17：83-107.

[10] ZHANG C W.On theL0-module structure for the generalized Witt algebra and the special Lie algebra[J].J Lie theory，2007，17(4)：709-729.

[13] ROTMAN J.An introducation to homological algebra[M].2nd ed.New York：Springer，2009：1-6.

[14] 张永正，刘文德.模李超代数[M].北京：科学出版社，2004：11-17..

(责任编辑：李亚军)

The centralizer of gl(0,2) in the generalized Witt Lie superalgebra over fields of prime characteristic

ZHENG Ke-li1，ZHANG Yong-zheng2

(1.Department of Mathematics，College of Science，Northeast Forestry University，Harbin 150040，China；2.School of Mathematics and Statistics，Northeast Normal University，Changchun 130024，China)

This paper is primarily concerned with the centralizer of gl(0,2) in the generalized Witt Lie superalgebra over fields of prime characteristic，where gl(0,2) is the subalgebra of the general linear Lie superalgebra.Firstly，the decomposition of the generalized Witt Lie superalgebra as a gl(0,2)-module is considered.Then the inner derivations from gl(0,2) into each submodules of the generalized Witt Lie superalgebra are calculated.Finally，the centralizer of gl(0,2) in the generalized Witt Lie superalgebra is completely determined by solving linear equations.

centralizer；Lie superalgebra；module；cohomology group

1000-1832(2016)04-0001-04

10.16163/j.cnki.22-1123/n.2016.04.001

2015-06-23

国家自然科学基金资助项目(11171055，11471090)；吉林省自然科学基金资助项目(20130101068)；中央高校基本科研业务费专项资金资助项目(2572015BX04).

郑克礼(1983—)，男，博士，讲师，主要从事李理论研究；张永正(1947—)，男，博士，教授，博士研究生导师，主要从事李理论研究.

O 152.5 [学科代码] 110·2130

A