双扩散传热传质模型及在横向谷冷通风中应用

王远成 杨开敏 潘 钰 张晓静 李福军 魏 雷

双扩散传热传质模型及在横向谷冷通风中应用

王远成1杨开敏1潘 钰1张晓静1李福军2魏 雷2

（山东建筑大学热能工程学院1，济南 250101）
（国家粮食局科学研究院2，北京 100037）

首先建立了单颗粒小麦内部水分迁移模型，基于有限元的方法数值模拟了颗粒内部水分变化规律，通过回归数值模拟数据，得到了颗粒平均水分模型和平均水分变化的干燥（或吸湿）速率模型。在此基础上推导出了谷物颗粒堆积床双扩散传热传质模型，并采用有限元的方法数值模拟分析了就仓横向（水平）谷冷通风时仓储粮堆内部热湿耦合传递规律。通过比较数值模拟和试验测定数据，验证了所建立的模型的合理性。分析了横向谷冷通风时粮粒温度和水分以及粮粒周围空气温度的变化规律，探讨了横向谷冷通风时粮堆内部降温效果。

谷物颗粒 双扩散 传质传热 仓储粮堆 横向谷冷通风

粮食颗粒具有吸湿和解吸湿特性，粮食在储存过程中水分会发生迁移和再分配，可能导致粮食的水分超过安全水分。由于粮堆水分的迁移直接与粮堆内部的温湿度相关，因此，预测和控制粮堆温度和水分是确保粮食安全储藏的关键［1］。粮堆中水分的迁移分为两个过程，即粮粒内部的水分扩散以及粮粒表面与周围空气中水蒸汽的对流交换。显然，粮堆的水分迁移取决于粮粒内部的水分扩散速度和粮粒表面对流扩散速度。

粮堆是由粮粒堆积而成的，粮堆内部热湿传递涉及到粮粒尺度和粮堆尺度，是一个多尺度多场耦合传递的问题。要研究粮堆内部水分迁移规律，首先要掌握单个粮粒内部的水分扩散规律，并由此进一步扩展到颗粒群（粮堆）。目前国内外采用数值模拟方法研究通风情况下粮堆内部热湿耦合传递的模型主要是以Thorpe建立的模型［2］。但该模型是基于多孔介质体积平均原理，而且假设粮堆内部粮粒温度与粮粒周围空气的温度相同，即满足“局部热平衡”。这种模型可以较好地反映粮堆内部温度和水分分布特点，但是由于粮粒内部的热质扩散与粮粒周围空气中热质扩散速度的不同，粮粒与周围空气之间本质上存在一定的温差，即二者的温度并不完全相同。因此，该模型就不能描述和区分粮粒和周围空气的温度差别。

本研究通过模拟分析单颗粒粮食内部的水分变化规律，首先得到了单个粮粒平均无量纲水分随时间变化的干燥（或吸湿）速率模型和干燥（或吸湿）常数，然后将单个粮粒平均水分模型扩展到具有一定孔隙率的堆积颗粒床（粮堆）的传质模型。同时，根据能量守恒原理，建立粮堆和周围空气的双扩散传热方程和传质方程，从而获得一种新的谷物颗粒堆积床的双扩散传热传质模型。通过有限元的方法数值求解的双扩散热湿耦合传递模型，分别获得了横向谷冷通风时仓储粮堆内部粮粒和周围空气的温度以及粮粒水分的变化规律。

1 粮堆热湿耦合传递模型

1.1 单粮粒水分迁移

真实粮粒大多是椭球形的而且各向异性［3-4］，然而，研究表明，对于像粮粒这样尺寸较小的颗粒，各向异性可以忽略不计，即近似认为是各向同性的，并且认为各向同性的椭球体和球体的扩散系数是一致的［5］。因此，把粮粒近似看作为一个球体，并且认为其内部水分扩散符合菲克扩散定律。粮粒内部水分扩散方程为：

式中：下标k表示粮粒内部。由于粮粒周围是空气，其表面适用于对流边界条件：

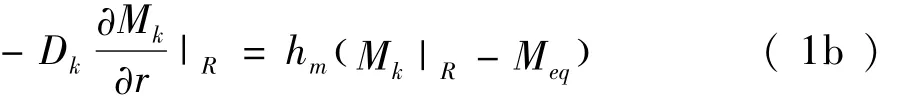
式中：Mk是粮粒内部的水分，Meq是平衡水分，粮粒内部水分扩散系数Dk＝Akexp（-Bk／T），其中的Ak与Bk是常数，T是粮粒的周围空气温度。对于软麦，Ak＝0．020m2／s，Bk＝6 155K；对于硬麦，Ak＝0．010m2／s［3-4］。当气温在0 ～ 20 ℃ 范围内，Dk≈10-11～ 10-12m2／s，而热扩散系数是ak≈10-8m2／s［5］，ak比Dk大约高三个数量级。这说明相对于质扩散而言热扩散要快得多，局部空气热量可以很快传递到整个粮粒。表面的传质系数hm，通常是从舍伍德数Sh求得的，Sh＝hmdm／Da。式中，Da是空气中的水分扩散系数（类似于表面传热的努塞尔数，Nu＝（h／ρC）dk／a）。例如，对于Sh≈5，和Da≈0．26 ×10-4m2／s当粮粒的当量直径dk＝4 mm时，hm≈0．31 m／s。

为了求解方程（1a，1b），引入无量纲参数：m ＝(M-Meq)／(M0-Meq)，ξ＝ r／R ，τ ＝ t／tk，tk＝d2k／4Dk＝ 3．7 × 105s，方程（1a）和（1b）可表示为

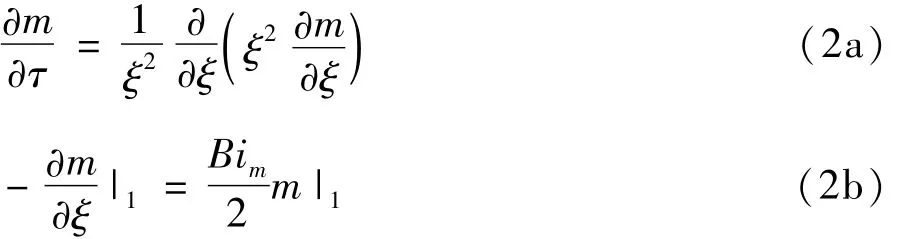
式中：Bim是传质毕渥数，Bim＝hmdk／Dk≈1．2×107。然而，如此大的传质毕渥数意味着粮粒内部水分传递阻力远远大于表面阻力。换言之，表面水分近似呈现平衡水分Meq，因此，对于实际情况，边界条件（2b）可以被改写为

通过求解方程（2a和2c），可以得到粮粒内部无量纲水分分布如图1所示，当时间t／tk＝0.112，从中心到边界浓度有一个光滑的变化表面。

1.2 单粮粒平均水分模型

回归方程（2）的模拟数据，可以得到粮粒平均无量纲水分的时间变化率（d／dτ）和粮粒无量纲平均水分（），如图2所示。从图2中可以看出，除了初始阶段始这2条曲线呈指数式衰减以外，在很长时间粮粒平均无量纲水分的时间变化率（d／dτ）和粮粒平均无量纲水分（）基本是平行的，二者比例因子为12。因此，这种水分传输模式可以由公式描述：

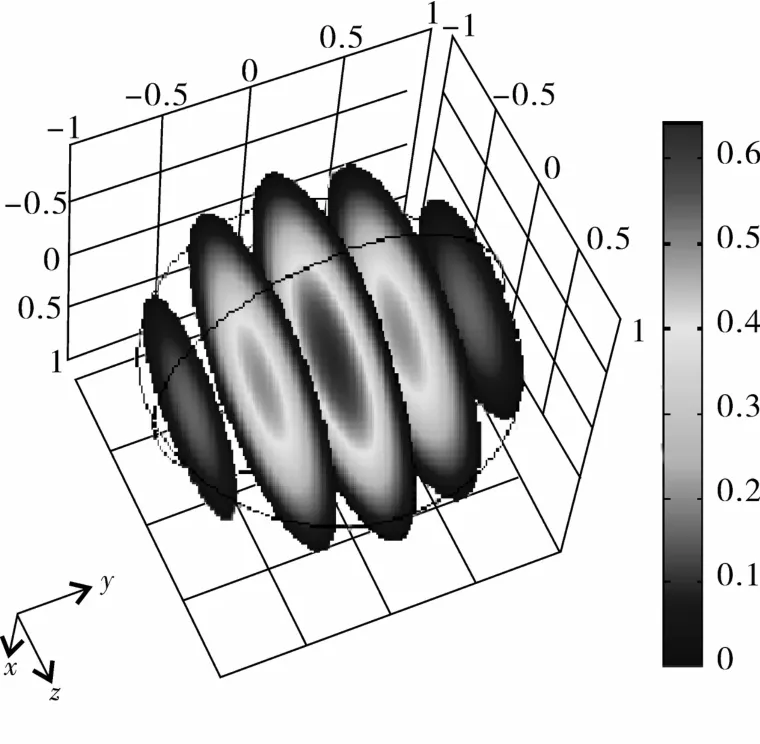
图1 粮粒内部无量纲水分分布

式（3a）即为单个粮粒平均无量纲水分随时间变化的干燥（或吸湿）速率模型，β为干燥（或吸湿）常数。β与O’Callaghan研究结果基本一致［6］。

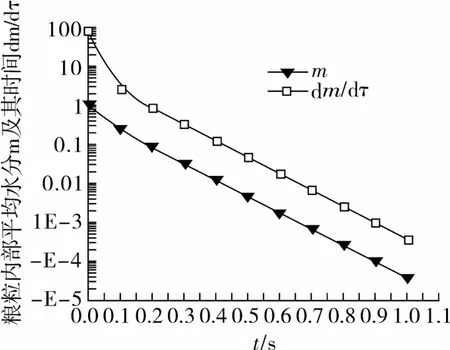
图2 粮粒平均无量纲水分随时间变化规律

对于密度为ρk，体积和表面面积分别为V1k和S1k的粮粒，其表面的水分扩散通量等于其内部水分变化率，类比热量传递中牛顿冷却公式，可以得到：

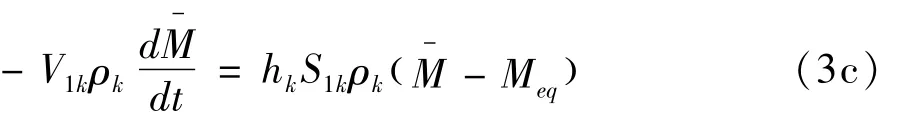
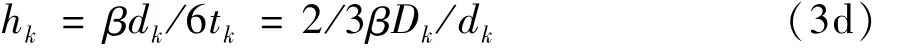
从式（3d）可以推出，有效表面对流传质系数hk≈10-8m／s，比较hk和hm，可以发现，hk远远小于hm。说明粮粒的平均水分传输速率主要取决于内部扩散，而不是取决于外部舍伍德数Sh。在式（3c）中的平衡水分取决于空气中的水蒸分气压，可以使用Chung-Henderson 相关进行计算［7］：

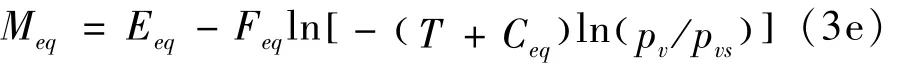
式中：相对湿度为r ＝ pv／pvs，Eeq、Feq和Ceq为常数，单位为摄氏度。水蒸气压力pv与比湿度（绝对含湿量）ω 相关，ω ＝ 0．622Pv／( p／pv)≈ 0．622pv／p＝ 0．622rpvs／p，其中，p为粮堆中大气压力，pvs为饱和蒸汽压［2］。由于pv与温度有关，因此，Meq＝ Meq( ω，T ) 。

2 谷物颗粒堆积床的一维热湿传递方程

2.1 谷物颗粒堆积床水分传递方程

假设体积VT空间内有Nk粮粒，且粮粒自然堆积在一起。粮粒通过扩散方式转移到空气中的水分为Qm，且Qm＝ NmS1khkρk（M-Meq）。其中，固相（粮粒）体积Vs＝NkV1k＝（1-ε）VT，从而得到Nk＝（1- ε）VT／V1k，因此，Qm＝ （1- ε）VT（S1k／V1k）hkρk（M-Meq）。对于一个球体粮粒来说，S1k／V1k＝6／dk，每单位体积颗粒床（粮堆）的水分转移为：

式中：qVm为单位体积传质量。如果粮粒以表观速度US被带入控制量VT＝A dx，那么，固相（粮粒）中水分的变化率为［8］：

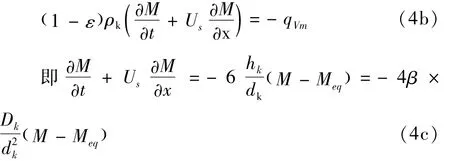
对于静态谷物颗粒堆积床（仓储粮堆）来说，粮粒的速度Us＝0，所以，

粮粒周围空气中水分指的是比湿度（绝对含湿量）ω，即空气中水蒸气的质量除以空气的质量。根据质量守恒定律，通过对流离开粮粒的水分qVm被流速为Ua的空气获得，即

2.2 谷物颗粒堆积床传热方程

从空气到固相（粮粒）的相间传热类似于水分的传递，即

式中：qV为单位体积传热量，Q为传热量，ha为有效表面对流传热系数，当小麦来说，ha＝3．7×10-6W／（m2·K）［9］。此时，传热毕渥数Bi ＝hadk／αk≈1．7，即意味着粮堆尺度的传热的内外热阻阻力比较接近，内部热阻稍大于表面热阻。根据热力学第一定律，速度为Ua的空气流中焓的增加等于来自于粮粒中的对流传热量与空气中水分变化获得的热量之和，即

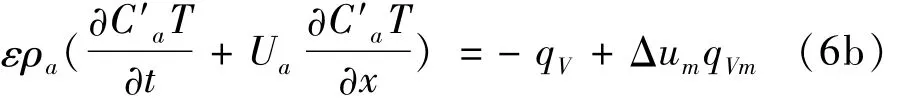
水分的内能Δum＝ Cm（Ts-Tm0），其中，Tm0为参考温度，Cm为粮粒水分的比热容。因此

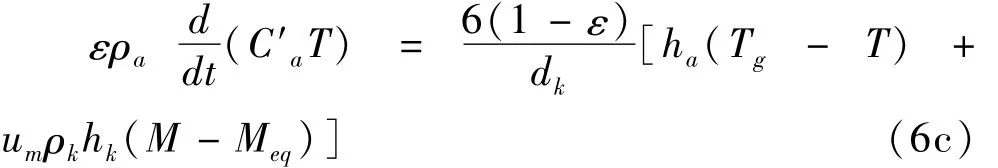
式中：空气的有效比热是C′a＝Ca+ωCm，Ca为空气的比热容。

根据热力学第一定律，固相（粮粒）中焓的增加等于粮粒与空气之间的热交换qV，再减去水分交换带走的热量，同时还要减去因粮粒的水分蒸发带走的热量。即

对于仓储粮堆来说，由于粮粒的速度Ug＝0，所以

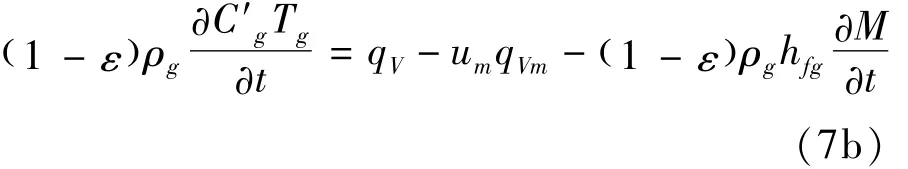
式中：粮堆的有效比热C′g＝Cg+CmM，hfg为粮粒水分蒸发的潜热。

因此，对于仓储粮堆来说，通风时粮堆内部热湿耦合传递的方程分别为式（4d）、式（5）、式（6c）和式（7b）。

3 模型应用和结果分析

基于前面建立的模型，采用有限元的方法数值模拟分析了就仓横向谷冷通风时仓储粮堆内部热湿耦合传递规律。房式仓的横向谷冷通风工艺如图3所示。横向通风就是把两组通风笼沿高度方向垂直安装在粮仓宽度方向的2个内墙上，通过吸式或吹式的方式实现了沿着粮仓宽度方向的横向通风。由于横向通风的通风笼1和2沿着粮仓长度方向均匀对称布置，因此，可以将横向通风近似看作沿着水平方向的一维流动和传热传质的问题。

房式仓长度为60 m，宽度为21 m，装粮高度为5.8 m，储存5 700 t小麦。小麦（粮堆）平均初温为32.2℃，平均湿基水分为12.2%（干基水分为13.98%）。粮堆的容重为ρg＝ 805 kg／m3，粮堆的比热容为Cg＝ 1 790 J／kg·K ，粮堆的孔隙度ε取为0.4。通风过程中采用的是分布式谷冷通风工艺，进风口空气的平均温度为17.5℃，相对湿度为85%，单位通风风量为4.9 m3／（h·t）。

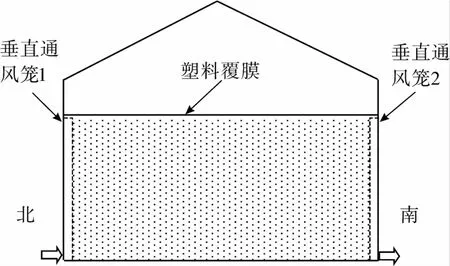
图3 房式仓横向通风网络示意图

图4 和图5是粮堆内部粮粒温度和粮粒周围空气温度以及粮粒水分在通风83.3 h时的变化规律。从图4可以看出，随着通风时间增加，粮粒温度逐步下降，通风终止时刻粮粒温度为24.34℃、粮粒周围空气温度为24.22℃，粮堆温度平均下降了7.86℃，粮堆内部空气的温度上升了6.72℃。从图3还可以看出，由于粮粒内部热阻大于粮粒表面空气的热阻，使得粮粒温度稍高于粮粒周围空气温度，二者始终相差0.15℃左右。由此看出，粮情监测系统显示的温度只是粮粒缝隙中空气的温度，而不是粮粒的真实温度。但是，由于粮粒温度和粮粒周围空气温度之差很小，工程上为了简化问题，可以近似认为粮堆内部是满足“局部热平衡”的［2］。图5是粮堆平均水分演化规律，可以看出随通风时间的增加，粮堆的平均水分逐步下降，水分从12.2%降到12.07%，降水幅度为0.15%，水分降低很小。这是因为采用分布式谷冷通风时进风口的空气湿度为85%，即进风的空气湿度较高，因此，通风过程中粮堆的水分降低较少。

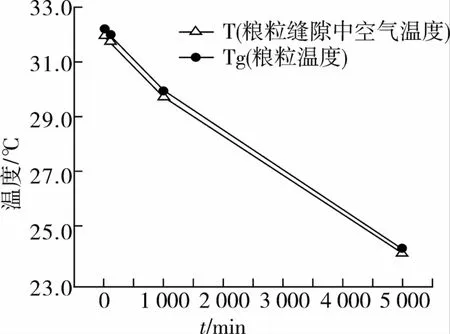
图4 粮粒温度及其中空气温度时间变化规律

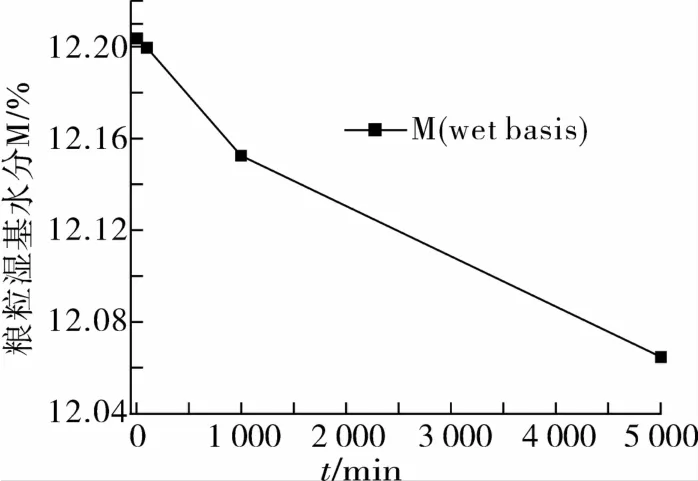
图5 粮粒平均水分时间变化规律

图6 是数值模拟的平均温度与清苑库横向分布式谷冷通风时测定的温度的比较（试验中没有测定水分），从图6还可以看出，数值模拟与试验测定结果基本相符，说明本文建立数学模型可以用于储粮通风的模拟研究。图7是不同通风时刻粮仓宽度上粮堆中空气温度分布。从图7可以发现，在通风的初始阶段（通风时间小于10 min），除了通风道入口附近的粮堆以外，粮堆内部空气的温度与粮堆的初始温度基本相同。分析其原因，主要是由于温度为17.5℃的空气中的含热量要远远小于温度为32.2℃粮堆的含热量，由于冷空气与粮堆的热量交换，空气的温度迅速接近粮粒的温度。因此，在距离通风道入口1米处，粮堆中空气温度在0.1 min内就达到了粮堆的温度。随着通风时间增大，空气的温度波的前沿不断前移，粮堆内部空气的温度逐渐升高。当通风时间到达5 000 min（83.33 h）时，整个粮堆内空气的平均温度到24.22℃左右。

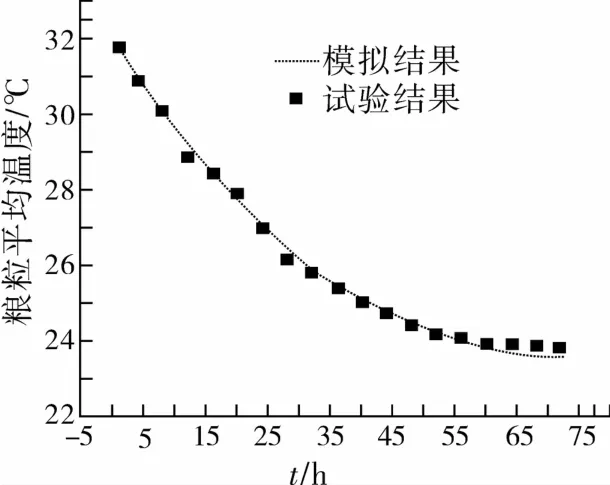
图6 数值模拟和实验测定的粮粒平均温度比较

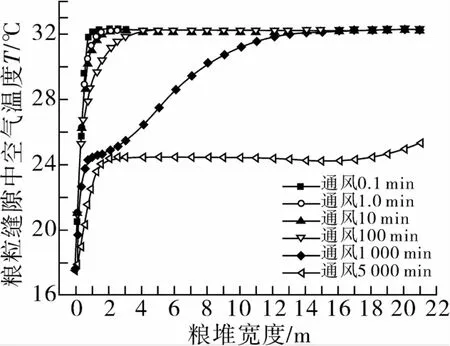
图7 不同通风时刻粮仓宽度上粮堆中空气温度

图8 是不同通风时刻粮仓宽度上粮粒（粮堆）的温度分布。从图8可以看出，在冷空气与粮堆的热量交换过程中，由于粮堆的热容量较大，粮粒温度下降较慢。在通风时间小于100 min情况下，粮堆只是在通风道入口1 m处，粮粒温度才开始下降。随着通风时间增大，粮粒的温度逐步降低。在通风时间到达1 000 min（16.67 h）时，粮堆中心区域粮粒温度开始下降；当通风时间到达5 000 min（83.33 h）时，整个粮堆温度都低于24.34℃。

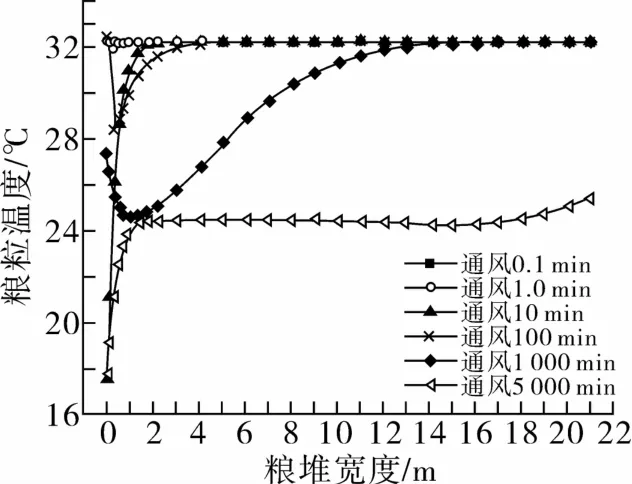
图8 不同通风时刻粮仓宽度上粮粒温度

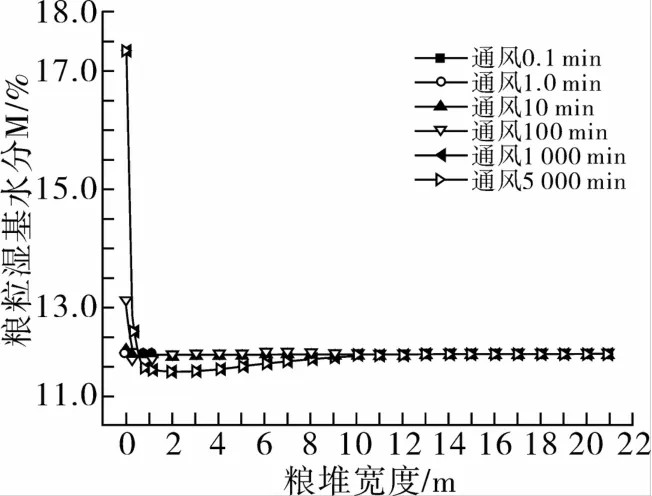
图9 不同通风时刻粮仓宽度上粮粒水分

图9 是不同通风时刻粮仓宽度上粮粒（粮堆）水分分布。从图9可以看出在整个通风过程中，下降幅度在0.2%左右，从图5也可以看到这个规律。正如前面的分析，这是因为通风进风的空气湿度较高（85%）的缘故。从图9中还可以看出，尽管粮堆的平均水分下降的很少，但在通风道入口处，粮堆的水分有明显的升高，到达了17.5%。这是由于在入口处发生了粮堆水分升高现象。对于入口水分升高的问题，可以通过内部环流通风或局部通风加以解决。

4 结论

本研究基于单个粮粒内部水分扩散的数值分析，建立了双扩散传热传质模型。基于双扩散传热传质模型，采用有限元的方法数值模拟分析了横向谷冷通风时粮粒温度和水分以及粮粒周围空气温度的变化规律。

4.1 粮粒（小麦）的传质毕渥数为1.2 ×107，粮粒内部水分传递阻力远远大于表面阻力，粮粒的水分传输速率主要取决于内部扩散速率的大小。粮粒（小麦）的传热毕渥数为1.7，粮粒内部传热热阻略大于粮粒表面空气的热阻，粮粒与周围空气之间存在一定的温差，但温差较小，工程上可以忽略。

4.2 横向谷冷通风83.3 h，仓内粮堆温度从32.2 ℃降低到24.2℃，降温幅度为8.0℃。水分从12.2%降到12.0%，降水幅度为0.2%。横向通风过程水分损失较小，降温效果明显。

4.3 通风道入口处粮堆的水分有明显的升高，入口处发生了粮堆水分升高的现象。

4.4 所建立的模型可以用于就仓通风的数值模拟研究以及干燥器的设计。

［1］王远成，亓伟，张中涛.圆筒仓内自然对流对粮堆热湿传递的影响研究［J］.水动力学研究与进展，2014，29（4）：487-496

Wang Y C，Qi W，Zhang Z T.The effect of natural convection on heat and moisture transfer of stored grain in a silo［J］.Chinese Journal of Hydrodynamics，2014，29（4）：487-496

［2］Thorpe G R.The application of computational fluid dynamics codes to simulate heat and moisture transfer in stored grains［J］.Journal of Stored Products Research，2008，44：21-31

［3］Brooker D B，Bakker-Arkema F W，Hall CW.Drying and storage of grains and oil seeds［M］.Chapman＆ Hall，New York，1992：217-220

［4］Ghosh PK，Jayas D S，Gruwel M L H.Mathematical modeling of wheat kernel drying with input from moisture movement studies using magnetic resonace imaging （MRI），Part I：Mode development and comparison with MRI observations［J］.Biosystems Engineering，2008，100（3）：389-400

［5］Gaston A L，Abalone R M，Giner SA，et al.Effect of modelling assumption on the effective water diffusivity in wheat［J］.Biosystems engineering，2004，88（2）：175-185

［6］O′Callaghan J R，Menzies D J，Bailey P H.Digital simulation of agricultural drier performance ［J］.Journal of Agricultural Engineering Research，1971，16：223-244

［7］Chung D S，Pfost H B.Adsorption and desorption of water vapor by cereal grains and their products.Part I：Heat and free energy changes of adsorption and desorption ［J］.Transactions of the American Society of Agricultural Engineers，1967，10：549-555

［8］Tien C.Adsorption calculations and modeling：fixed-bed moisture function ［M］.Butterworth-Heinemann，Newton，MA，1994：231-245

［9］Jayas D S，Cenkowski S，Pabis S，et al.Review of thin layer drying and wetting equations［J］.Drying Technology，1991，9（3）：551-588.

A Double-Diffusivity Heat and Moisture Transfer Model and Simulation of the Cooling Aeration of Stored Grain in a Warehouse with a Horizontal Air Flow

Wang Yuancheng1Yang Kaimin1Yu Pan1Zhang Xiaojing1Li Fujun2Wei Lei2
（College of Thermal Energy Engineering，Shandong Jianzhu University1，Jinan 250101）
（Academy of the State Administration of Grains2，Beijing 100037）

A diffusive moisture transfer equation for a single grain kernel was presented and solved with Finite Element Method（FEM），moisture content distribution inside the kernel were examined，and the average non-dimensional moisture content and its time-rate of change were obtained.By regression these numerical data，a kernel-average moisture model was derived，which was extended to volumetric mass transfer for a bed of kernels.Based on the kernel-average moisture model，the one-dimensional double-diffusivity heat and moisture transfer model were derived for a stationary bed of kernels，and were solved to simulate the evolution of grain temperature and moisture content of stored wheat in a warehouse during the cooling aeration with a horizontal air flow.Validation was performed by comparing between predicted and measured grain temperature and moisture content of Grain depot.Predicted data were in reasonable good agreement with measured ones，and the effect of the aeration was also evaluated.

a single grain kernel，double-diffusivity，heat and mass transfer，stored bulk grain，cooling aeration

TH432

A

1003-0174（2016）11-0106-06

国家自然科学基金（51276102），国家粮食公益专项（201513001），国家重点专项（2016YFD0400100，2016YFD0401002）

2015-02-15

王远成，男，1963年出生，教授，复杂系统流动和传热传质和储粮生态系统热湿传递