带有调压室的长距离引水系统水力特性研究

化 卓，张永良

(1.江苏省河道管理局，南京 210029；2.清华大学 水利水电工程系 水沙科学与水利水电工程国家重点实验室，北京 100084)



带有调压室的长距离引水系统水力特性研究

化 卓1，张永良2,*

(1.江苏省河道管理局，南京 210029；2.清华大学 水利水电工程系 水沙科学与水利水电工程国家重点实验室，北京 100084)

为了解和掌握带有调压室的长距离引水系统的特殊水力特性，依托锦屏二级水电站，采用压力引水系统水力过渡过程的数学模型，计算和分析了引水隧洞长度对引水系统大波动过渡过程的影响，考虑在各种大波动过渡过程中不利工况情况下，分析了阻抗式和差动式两种型式调压室引水系统的水力特性，揭示了长距离引水隧洞沿线压力分布、调压室涌浪特性、蜗壳进口压力随引水隧洞长度变化的规律。

调压室；长引水隧洞；水力特性；涌浪；水击

图1 带有调压室的引水系统示意图Fig.1 Schematic diagram of water headrace system with a surge chamber

随着我国水电事业的发展，引水式水电站的开发方式由于坝体高度低且可以降低建设成本、淹没损失、移民数量和对生态环境的影响等优点，在西南山区得到广泛应用。有些水电站由于受地形条件的限制不得不修建10 km量级的长距离引水隧洞，有的引水隧洞甚至超过了15 km，如锦屏二级水电站引水隧洞长16.67 km，属超长距离引水系统(图1)。由于引水隧洞超长、水流惯性大，调压室内的水体波动周期长、振幅大、衰减缓慢[1-5]，这给水电站大波动过渡过程带来了一些新的问题。为此，许多学者对此进行了一系列的研究。

陈祥荣等[5]结合锦屏二级水电站进行了水力计算，指出长距离引水隧洞水电站由于水击波反射较慢，故存在与短引水隧洞水电站所不同的特殊水力学问题，主要有引水隧洞沿线的最高和最低压力分布规律；蜗壳进口处水击压力与最高压力发生时刻；不同导叶关闭时间对阻抗式和差动式调压室的各自蜗壳进口压力变化的影响；阻抗孔口面积的大小对水击压力、穿室压力大小不同程度的影响等。陈长值等[6]指出在隧洞很长的情况下，隧洞的糙率对调压井内水体的波动影响很大。付亮等[7]以锦屏二级水电站为例分析了超长引水隧洞水电站在大波动过渡过程方面的特点，指出一般情况下上游管线内最大、最小压力分布均受到上游调压室最高、最低涌浪的控制，并分析了阻抗孔口大小、调压室与厂房距离、导叶关闭时间等因素对蜗壳最大压力的影响。杨鹏等[8]计算分析了压力管道的直径对水击压力的影响。上述研究大多是结合某一工程实例固定引水隧洞长度而改变其他参数来研究其水力特性，尚未有文献报道长距离引水系统中引水隧洞长度对水力过渡过程特性的影响。本文将研究引水隧洞长度对大波动过渡过程水力特性影响的规律，从而掌握高水头、大容量的超长距离引水系统水力特性，为开发这类水电站提供理论依据。

1 数学模型

引水系统中有压瞬变流的运动方程和连续方程分别为：

(1)

(2)

式中H为从某一基准面算起的测压管水头；V为管道中的水流流速；x为沿管道轴线指向下游的距离坐标；t为时间；f为Darcy-Weisbach摩擦系数；D为管道的直径；θ为管道轴线与水平面的夹角；g为重力加速度；a为水击波速。

阻抗式调压室(图2)内水体的连续方程和动量方程分别为：

(3)

(4)

图2 阻抗式调压室Fig.2 Throttled surge chamber

图3 差动式调压室Fig.3 Differential surge chamber

式中QT为引水隧洞的流量；Qs为流入或流出调压室的流量；Q为高压管道的流量；As为调压室内的水面面积；Hs为调压室水位；H1为调压室底部测压管水头；H2为调压室测压管水头；fs为调压室沿程阻力系数；Ds为调压室直径；l为调压室的水深。

差动式调压室(图3)节点P、E和主室的连续性方程分别为：

QT=Q+Qs,Qori=Qs-Qz,Qss=Qori+Qy

(5)

式中Qz为升管流量；Qori为主室阻抗孔口的流量；Qss为主室的流量，由式Qss=Ass(dHss/dt)给出，其中Hss为主室水位，Ass为主室截面积；Qy为升管溢流流量，由下式确定：

(6)

式中k11和k12分别为水从升管流入主室时的非淹没溢流系数和淹没溢流系数；k21和k22分别为水从主室流入升管时的非淹没溢流系数和淹没溢流系数；By为升管溢流堰的宽度。

调压室室段L1(L1=Z1-Z0)、升管、主室的动量方程分别为：

(7)

(8)

(9)

式中Ar为升管截面积；Dr为升管的直径；fr为升管的沿程阻力系数；σ为调压室进口局部阻力系数；HP为点P的测压管水头；HE为点E的测压管水头；HF为主室点F的测压管水头；Dss为主室水力当量管的直径。

2 研究方法及计算参数

为了认识长距离引水隧洞的特殊水力学问题，比较各种长度引水隧洞的水力学特性。依托锦屏二级水电站工程，分析隧洞长度对引水系统过渡过程的影响。具体的研究和考虑的方法为：①在引水系统各参数(不包括调压室面积)不变的情况下，考虑了各种长度的引水隧洞；②对于不同长度的引水隧洞，相应的调压室断面面积将随之改变，即由托马稳定断面面积公式所求得的调压室面积再乘上安全系数，而安全系数不随调压室临界稳定断面面积的改变而改变。在上述方法下，探索引水系统中大波动和水击的水力要素随隧洞长度的变化规律。

锦屏二级水电站计算参数：1号引水隧洞长度为16 700 m，等效洞径12 m，等效糙率为0.018，调压室处引水隧洞分叉成两条压力管道(等效长为600 m，直径7.5 m)与两台机组相连，额定水头为288 m，机组额定流量为232.5 m3/s。水轮机采用直线关闭规律，导叶关闭时间13 s，开启时间60 s。对于超长引水隧洞的水电站，存在波动叠加的可能，计算时需要考虑各种叠加工况，共5种工况(表1)。在下面两节中，采用特征线法求解引水系统水流的微分方程。

表1 计算工况

Table 1 Different calculation cases

工况水位组合水轮机工作情况计算目的G1G2G3上、下游校核洪水位1658m、1352.4m两台机全荷运行同时甩全荷隧洞沿线最高压力分布,蜗壳进口最大压力两台机全荷运行,一台机甩全荷,经ΔT另一台机甩全荷蜗壳进口最大压力两台机不间断连续增全荷,经ΔT同时甩全荷调压室内最高涌浪G4G5上游死水位1640m、下游水位1325.9m两台机全荷运行并同时甩全荷,经ΔT1一台机增全荷,再经ΔT2另一台机增全荷调压室内最低涌浪一台机全荷运行,另一台机增全荷隧洞沿线最低压力分布

3 隧洞长度对管道内水压的影响

3.1 引水隧洞沿程最高、最低压力分布

引水隧洞沿程压力分布是引水隧洞、调压室结构设计的重要依据，与短引水隧洞沿程压力分布不同，长距离引水隧洞的压力并非直线分布。为了认识长、短引水隧洞沿程最高、最低压力分布的不同，特选定引水隧洞长16 700、12 700、8 700、4 700 m在工况G1和G5(表1)下进行计算，分别求隧洞沿程最高、最低压力分布。引水隧洞沿程最高和最低相对压力水位(Hmax/Hup、Hmin/Hup)的分布见图4和图5，其中Hmax、Hmin和Hup分别为最高压力水位、最低压力水位和上游库水位。

图4 引水隧洞沿程最高相对压力水位分布，左图为阻抗式；右图为差动式Fig.4 Distribution of maximum relative pressure along the headrace tunnel,throttled surge chamber (left);differential surge chamber (right)

图5 引水隧洞沿程最低压力水位分布，左图为阻抗式；右图为差动式Fig.5 Distribution of minimum relative pressure along the headrace tunnel,throttled surge chamber (left);differential surge chamber (right)

由图4、图5可见，从上游进水口(x/L=0)至下游方向，引水隧洞沿线最高压力水位分为上凸增曲线，最低压力水位分布曲线几乎为线性递减，其原因在于，最低压力水位分布是在工况G5情况下得到的，即低水位下一台机正常运行另一台机启动时，该工况下调压室补水较快，隧洞流速变化梯度很小，因此穿室的负压水击较小，从而使隧洞的最低压力水位分布几乎成直线。最高压力水位分布曲线中，差动式调压室对应曲线比阻抗式调压室对应曲线上凸更显著。这是因为差动式调压室结构灵敏，水位波动衰减较快，其对应的最大水击压力要大于阻抗式对应的最大水击压力。阻抗式最高、最低压力水位及差动式最低压力水位分布曲线均为单调增、减曲线，而差动式最高压力分布的上凸曲线存在峰值。对于差动式调压室系统，引水隧洞长16 700、12 700、8 700、4 700 m时，最高压力曲线的峰值分别出现在上游距调压室5 010、3 810、1 740、470 m的洞线处，且其上凸特性依次减弱。由此可见，引水隧洞越长，差动式调压室所对应的最高压力水位分布曲线上凸特性越明显，且上凸曲线的峰值越往上游方向移动。

3.2 蜗壳进口压力升高

水击与涌浪是设置有调压室的电站在过渡过程中发生的两种主要物理过程，压力管道压力上升就是由这两种过程的联合作用造成的。由于水轮机导叶关闭时间通常较短(约10 s)，如果忽略这段时间内调压室底部压力升高(通常是由于调压室在这段时间内的水面升高以及水流进入调压室时的局部水头损失或者调压室中气体压力的升高造成的)，水击引起的最大压力升高的最主要因素是压力管道长度、压力管道中水流流速以及导叶关闭时间和关闭规律，这些因素与引水隧洞的长度并没有直接的联系，但这些因素与引水隧洞的长度会共同影响蜗壳进口处的水击压力。在计算工况G2(表1)下，蜗壳进口压力升高(ΔH)和压力相对升高(ΔH/Hmax,其中Hmax为蜗壳进口最大压力)随隧洞长度变化规律分别见图6和图7。

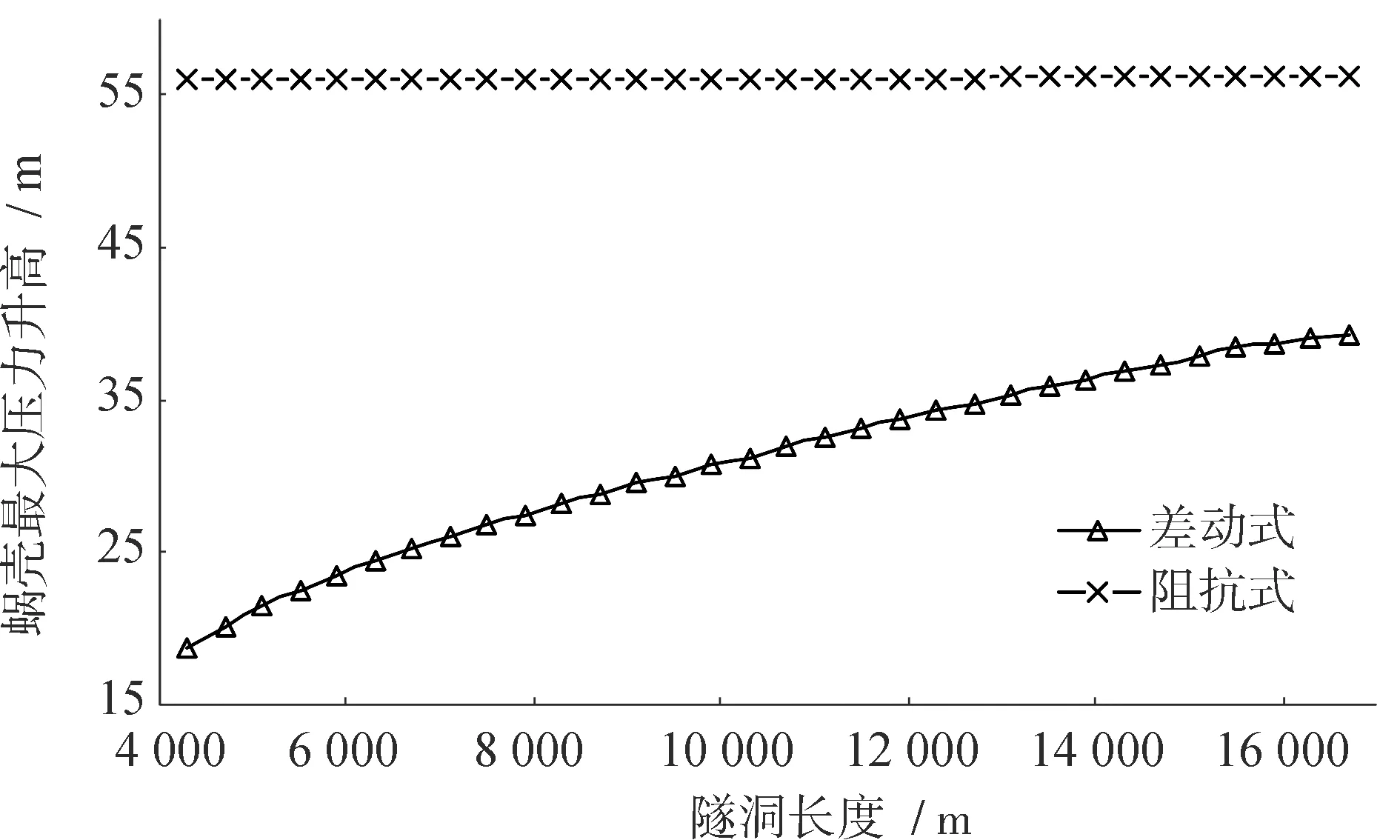
图6 蜗壳压力升高随隧洞长度的变化曲线Fig.6 Variation of water pressure increment at volute casing inlet with tunnel length

图7 蜗壳压力相对升高随隧洞长度的变化曲线Fig.7 Variation of relative water pressure increment at volute casing inlet with tunnel length

由图6、图7可见，阻抗式和差动式调压室系统蜗壳进口压力升高都是弱非线性增加的，但阻抗式调压室系统对应的蜗壳进口压力升高对隧洞长度不很敏感，随着引水隧洞长度的增加，蜗壳进口处压力升高值增大不明显，即隧洞长度从16 700 m缩短到4 300 m，蜗壳相对压力升高的变化并不太大(压力相对升高从56.25 m到56.01 m)，相对升高百分比从3.31%到3.28%。而对于差动式调压室系统，蜗壳进口压力升高则对隧洞长度较为敏感，隧洞长度从16 700 m减小到4 300 m，差动式对应的蜗壳相对压力升高从39.31m到18.78 m，相对升高百分比从2.35%到1.12%，即随隧洞长度的增大压力升高值增大相对显著。

4 隧洞长度对室内大波动的影响

调压室内质体的波动直接影响到电站建设工程量和电站的发电品质。下面对阻抗式、差动式两种型式调压室系统分别研究引水隧洞的长度对调压室涌浪幅值、涌浪衰减、波动周期、振幅的影响。

4.1 调压室内涌浪

在控制工况G3(表1)下阻抗式和差动式调压室内质体波动的最高涌浪随引水隧洞长度的变化见图8。由图8可见，调压室最高涌浪高度与引水隧洞长度有密切关系，随着引水隧洞长度增加，调压室最高涌浪高度增大，最高涌浪与隧洞长度呈弱非线性关系，且为上凸曲线，阻抗式调压室的非线性要比差动式的大。

最低涌浪的控制工况是G4(表1)，叠加时间选用安全开机时刻，选取流入调压室流量最大的时刻为ΔT1、下一个波动周期流出调压室流量最大时刻为ΔT2。阻抗式、差动式调压室内质体波动的最低涌浪随引水隧洞长度的变化见图9。由图9可见，随着引水隧洞长度的增加，阻抗式和差动式调压室最低涌浪高度减小；最低涌浪与隧洞长度呈弱非线性关系，且为下凹曲线；差动式调压室最低涌浪随隧洞长度的非线性要比阻抗式的大。

图8 最高涌浪随隧洞长度的变化曲线Fig.8 Variation of maximum mass oscillation with tunnel length

图9 最低涌浪随隧洞长度的变化曲线Fig.9 Variation of minimum mass oscillation with tunnel

G1工况(表1)下阻抗式和差动调压室最大振幅随隧洞长度的变化见图10，由于其它各种工况的结果极为类似，在此不再赘述。由图10可见，随着引水隧洞长度增加，调压室最大振幅增大；当引水隧洞长度达到约12 km后，阻抗式调压室的最大振幅要比差动式的大；调压室的最大振幅与隧洞长度呈弱非线性关系，差动式的非线性性要比阻抗式的大。

4.2 调压室波动周期

调压室的波动周期是影响发电品质的一个重要因素，因此深入分析隧洞长度对波动周期的影响规律很有必要。G1工况(表1)下阻抗式和差动调压室平均波动周期随隧洞长度的变化规律(其它各种工况的结果极为类似，在这不再赘述)见图11。由图11可见，阻抗式和差动式调压室波动周期随着引水隧洞长度增加而增大；阻抗式和差动式调压室的波动周期与隧洞长度都呈上凸增的弱非线性关系；在相同隧洞长度情况下，阻抗式调压室的波动周期要比差动式的大20%～26%。

图10 调压室内水体最大振幅随隧洞长度的变化曲线Fig.10 Variation of maximum mass oscillation amplitude with tunnel length

图11 调压室内水体波动周期随隧洞长度的变化曲线Fig.11 Variation of mass oscillation period in a surge chamber with tunnel length

5 结 论

采用带有调压室的长距离引水系统瞬变流数学模型，对长距离引水系统中分别带有阻抗式调压室和差动式调压室的瞬变流特性进行了研究，分析了调压室内的涌浪和管道内的水击压力与隧洞长度的相互关系。结果表明：

1)引水隧洞沿线最高压力分布曲线为上凸增曲线，最低压力分布为递减直线。最高压力水位分布曲线中，差动式调压室对应的曲线要比阻抗式调压室的上凸明显，且存在峰值。引水隧洞越长，差动式调压室所对应的最高压力水位分布曲线上凸特性越明显。

2)调压室内最高涌浪、最低涌浪、波动周期、最大振幅与引水隧洞长度有密切关系。隧洞越长，调压室最高涌浪越高，最低涌浪越低，波动周期越大，最大振幅也越大，变化规律呈弱非线性，反映出长距离引水系统振荡周期长、振幅大、衰减慢的特点；在涌浪方面，差动式调压室涌浪幅值与隧洞长度的非线性关系要比阻抗式的大；在波动周期方面，阻抗式调压室的波动周期要比差动式的大。

3)隧洞越长，蜗壳进口压力升高值越大，呈弱非线性增加。洞长对阻抗式、差动式调压室系统中蜗壳进口压力升高值影响程度不同，前者对蜗壳进口压力升高不甚明显，后者对蜗壳进口压力升高相对明显。

上述成果可为长距离乃至超长距离引水系统的设计提供指导。

[1] 张芹芬，索丽生.水电站水击与调压室涌浪随机分析研究进展[J].水利水电科技进展，1998，18(3)：7-11.(Zhang Qinfeng,Suo Lisheng.Advances on the random analysis of water hammer and mass oscillation in a hydropower system [J].Advances in Science and Technology of Water Resources,1998,18(3): 7-11.(in Chinese))

[2] 何文学，李茶青.水电站大波动过渡过程研究现状及发展趋势[J].水利水电科技进展，2003，23(4)：58-61.(He Wengxue,Li Chaqing.Research present situation and trend in development of large mass oscillation in hydropower pipeing system [J].Advances in Science and Technology of Water Resources,2003,23(4): 58-61.(in Chinese))

[3] 张永良，缪明非.组合工况下阻抗式调压室涌浪计算的显式公式[J].水利学报，2012，43(4)：467-472.(Zhang Yongliang,Miao Mingfei.Explicit formulas for calculating surges in throttled surge chamber [J].Journal of Hydraulic Engineering,2012,43(4): 467-472.(in Chinese))[4] 程永光，陈鉴治，杨建东.水电站调压室涌浪最不利叠加时刻的研究[J].水利学报，2004，35(7)：109-113.(Cheng Yongguang,Chen Jianzhi,Yang Jiandong.Study on the worst moment of superposed surge wave in surge tank [J].Journal of Hydraulic Engineering,2004,(7): 109-113.(in Chinese))

[5] 陈祥荣，沈家俊.长引水隧洞电站调压室的特殊水力学问题研究[J].红水河，1999，18(01)：61-68.(Chen Xiangrong,Shen Jiajun.Study on the special hydraulic questions of the surge chamber with long-distance diversion tunnel[J].Hongshui River,1999,18(1): 61-68.(in Chinese))

[6] 陈长植，郑双凌，马吉明.调压井试验中模型律及模型比尺的选择[J].实验技术与管理，2007，24(1)：20-22.(Chen Changzhi,Zheng Shuangling,Ma Jiming.Selecting of mode law and scale in surge tank model experiment[J],Experimental Technology and Management,2007，24(1)：20-22.(in Chinese))

[7] 付亮，杨建东，王建伟.超长引水隧洞水电站大波动过渡过程特殊问题[J].中国农村水利水电,2006(9)：112-117.(Fu Liang,Yang Jiandong,Wang Jianwei.Special problems of large oscillation transient process of hydropower station with long-distance tunnel[J].China Rural Water and Hydropower,2006,(9): 112-117.(in Chinese))

[8] 杨鹏，张健，陈胜，等.长引水系统水电站压力管道直径优化[J].水利水电技术，2015，46(3)：91-93.(Yang Peng，Zhang Jian，Chen Sheng，et al.Optimization on diameter of penstock for hydropower station with long diversion system[J],Water Resources and Hydropower Engineering,2015,46(3):91-93.(in Chinese))

Hydraulic characteristics of transient flow in long-distanceheadrace system with a surge chamber

HUA Zhuo1,ZHANG Yong-Liang2,*

(1.RiverManagementBureauofJiangsuProvince,Nanjing210029,China; 2.StateKeyLaboratoryofHydroscienceandHydraulicEngineering，DepartmentofHydraulicEngineering，TsinghuaUniversity，Beijing100084，China)

In order to understand and master the special hydraulic characteristics of long-distance headrace tunnel system with a surge chamber,this paper took Jinping II hydropower station as examples and studied the effect of headrace tunnel lengths on the large mass oscillation in long-distance headrace tunnel systems with a surge chamber by applying a mathematical model.Under several adverse cases the hydraulic characteristics of transient flow in the headrace tunnel system with either a throttled surge chamber or a differential surge chamber for various headrace tunnel lengths was explored.Results revealed the relationship between headrace tunnel lengths and water pressure in the headrace tunnel as well as between headrace tunnel lengths and penstock/large mass oscillation in the surge chamber.

surge chamber; long-distance headrace tunnel; hydraulic characteristics; mass oscillation; water hammer

10.13524/j.2095-008x.2016.04.049

2016-10-28

国家自然科学基金资助项目(51679124,51479092)

化 卓(1984-)，女，河南禹州人，工程师，研究方向：水工水力学、水利工程管理，E-mail:719781779@qq.com；*通讯作者：张永良(1964-)，男，浙江平湖人，教授，研究方向：水动力学、海洋流体-结构相互作用，E-mail: yongliangzhang@tsinghua.edu.cn。

TV732

A

2095-008X(2016)04-0001-07