数字河流河源判析

宋华标，刘新贵，赵云鹏，吴 铮

（1.信息工程大学，河南 郑州 450001）

数字河流河源判析

宋华标1，刘新贵1，赵云鹏1，吴 铮1

（1.信息工程大学，河南 郑州 450001）

通过对已有的一些判断原则进行分析，提出当河流长度占优势时以长度为主、连通性为辅；当长度相差不大时，以连通性为主的判断原则。通过该方法判断中国各地区主要河流河源的结果与科学考察结果一致。该方法对河流河源的实地考察具有一定借鉴意义。

数字河流；河源；判断原则；长度优先；连通性

1 河源判断原则

河流结构存在曲折复杂性、非均匀性和分支等特点，给河流源头的确定带来了很多麻烦。如何确定河流正源，目前国内外学术界尚未取得共识[1]。通过分析国内外判断河流源头的实例，归纳了如下主张：①“河源唯长”；②源流与下游干流流向比较一致[2]；③考虑流域面积与径流量；④考虑河谷发育期的早晚及源头的海拔高程等[3]；⑤以历史习惯作为标淮[4]。

这些是人们在判断河流源头时常用的原则，下面对这些原则在实际应用中的利弊进行简单分析。

2 判断原则分析

1）“流量为大”与“流域面积为大”原则。实际上河流流量、流域会受季节、气候地形或其多个二级以下河流汇流流量的影响；而且流量和流域面积数据也不好测量，在一般数据库中相关数据是缺失的。另外一条河流的源头河流是不能随便变动的，不应随河水量的变化而变化。所以，一般认为“流量为大”和“流域面积为大”的原则在判断河流源头问题上存在一定缺陷，不足以充当判断的充分条件，其时空差异性很大，客观性不足，一般不提倡[5]。

2）“河源唯长”原则。河流河源长度是确定河源的重要原则，但河流长度是很难测量的。无论是冰川还是泉眼，其本身就是一个变量[6]。在冰川或沼泽地区，长度的测算点在哪里，是冰川顶部还是边缘，是沼泽最外缘泉眼还是沼泽中出水量最大的点，这些起算点的确定都非常困难。而且河流的长度，也不可能精确到小数点后几位，按照长度判断有可能得出多个源头的情况。因此，单一考虑河流长度，对河流源头的确定有一定的困难。

目前还有一些河流存在“多源头”的说法。其实质是该河系主干流的河流源头还没明确确定。“多源头”的流行或许是为照顾历史习惯，或是地方的权益。但是“多源头”不宜提倡，就像一个人同时拥有两个识别码分别为“张三”、“李四”，对于那些认识且知道他有两个名字的人来说，他们的交流当然没问题，但当甲只知道他叫“张三”，乙只知道他叫“李四”，甲乙两人讨论他时，就会带来交流和认识上的麻烦，所以应该消除“多源头”的说法。

3）“与主流方向一致”原则。虽然河流河道流向受其初始流向、流经地域的岩性和相关地质构造运动等多种地表地质因素制约，但其在发育过程中不断分形、分化，不断地裁弯取直。因此，对于一条发育成熟的河流来说，主干流和支流在交叉处与主流方向的夹角必然是不同的，绝大多数的主干流与主流方向夹角比支流与其的夹角小，主流方向上的连通性更强，水流会更顺畅。虽然可能存在个别特殊情况，但在确定河源时，该原则应该成为重要的判断标准。

因此本文提出以下判断原则：①若河流长度存在明显差别，则以“河源唯长”原则为主，连通性为辅；②若河段在河流长度上没有优势，则以“与主流方向一致” 原则即连通性为主，充分考虑相交处的切线斜率或夹角，将此定性原则进行定量化，以夹角小或连通性好的河段为河流河源。

3 河流相交类型分析

一般线状地物如果出现交叉、分支，那么可能得到的结果类型可归纳为：

a、b、c、d可分别表示线段或弧形曲线段（为叙述方便，弧形曲线段和直线段都简称为线段）。利用如图1所示线段与线段之间的夹角θ来比较相交处的连通性。目前的研究发现，夹角在0～75°的曲线连通性被认为是较好的[7]。

图2为两条河段垂直相交的模型，b垂直交于a线段的一个端点。这种情况可以认为：a、b为同一条河流且可能是一条人工河。两段河流实为同一河流，那么这种情况无需判断就可知河源是上游段。

图1 线段相交夹角θ

图2 两河段垂直相交模型

图3中a、b、c表示河流河段，3条线段间交点处夹角可在0～180°之间变化，不同的角度可表示一般的Y型或T型。通过线段连接判断所形成线时的夹角或切线曲率（也有人称为顺直度），比较线的连通性，进而判断可能的相交类型。假设河水是从b、c往a方向流动，b、c在a的一段交汇，a与c交叉处的切线斜率要大于a与b相交在该点处的切线曲率，则认为a、b的连通性更好，则a、b更可能是同一条河流，即a、b应该具有同一地名属性。c应该是另外一条河流，有独立的地名归属。此时测量b、c的长度，当b、c线段在长度上没有优势比较时，将不再首先考虑“河源唯长”原则，这时主要考虑连通性，因为a、b连通性更强，所以b更应该是河流源头。

如图4所示， a、b、c、d线段交于一点，这种情况很可能是两条支流汇集在一条干流上。比较河水流向：如果a、b、c向d方向流动，那么测量a、b、c的长度，长度最长的确定为d的河流源头。特殊情况，若是两条主干河流相交，则存在两个流向。假设a、b可能向c、d方向流去，考虑“与主流方向一致”原则，若令a、d为一组，b、c为一组，则所有情况的连通性均较差。最理想的情况是a、c线段组成一条线，b、d线段组成另一条线，这样a、c，b、d都会具有较好的连通性，它们与主流方向的顺直度较好，a和c、b和d应该分别具有相同的地名属性，是两条河流、两条河源。

图3 3河段河流交汇模型

图4 4河段河流交汇模型

4 实验验证

4.1 实验数据

本实验数据来源于国家测绘地理信息局网站提供的全国矢量地图大全shp格式的河流数据。实验将对位于西北冰川、沼泽的长江发源地区和水系密集、河网复杂的中南地区的湘江源头的河流情况进行详细分析说明；还对存在过河源争议问题的河流，如西南地区的沧澜江、中原地区的汾河、东北地区的松花江和华东地区的钱塘江进行了判断验证（该部分列表说明）。

4.2 长江河源判断

图5为长江发源地区的河流分布图。首先进行一般性检验，通过数字河流可视化可以明确地排除很多不可能成为长江源头河流的河段。例如，可以很明显地判断e河段比a河段短，其他河段也都比a、b、d河段短，所以像e这样的河段就不需考虑其是否为长江的源头河段了。另外通过仔细观察可以发现，主干流交汇处上游干流与下游的连通性一般比支流与下游的连通性强。可以通过ArcGIS中测量工具测量或由属性表统计得出：length d=575 km，length ac=597 km，length bc=596 km，这时d、ac、bc的长度很相近，均不具有长度优势，此时通过定量测量河段交汇处的夹角进行判断，d与下游段的夹角明显比c与其下游段的夹角大，实际上图中d（楚玛尔河）与c段处的交角非常大，大概在110°～120°之间，其连接处的连通性较差，且长度比ac、bc段小，所以d不会是长江源头。那么此时a到c与b到c的交叉口，a代表的沱沱河长为340 km，b代表的当曲长为339 km，a、b两河段的长度相差不大，由于缺乏流量数据无法判断哪个河流段的流量更大以及发源地冰川或沼泽水源的情况。此时从通天河处作水平线，不难发现a与通天河的夹角约为10°比b与通天河的夹角20°小；因此主要通过连通性即交汇夹角或切线斜率来判断，沱沱河应该是长江的源头河流。

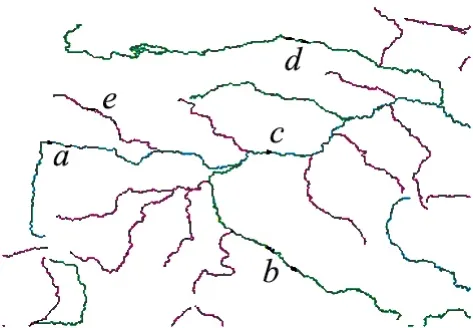
图5 长江河流发源地区河流情况

4.3 湘江河源及其他河流河源判断

图6为湘江海洋河和潇水河段图。首先考虑“河源唯长”原则，在ArcGIS中将数字河流可视化，并测量得到海洋河到与潇水汇合处的长度为204 km，潇水到交汇处的长度为284 km，潇水在长度上有优势；再看二者在交汇处的连通性情况：河流的数字化是根据河流的中心线采集的，此处夹角的测量主要就是利用中心线相交处的夹角来确定。因此中心线相交处数字化结果的好坏与作图者的知识与制图水平有很大关系。此时可以结合遥感影像图上水系的情况进行测量判断。本文结合shp格式数据和对Google遥感影像上的该段河流的测量发现，潇水段与下游的夹角θ约为38°，海洋河段的夹角θ约为12°，二者的连通性都较好。但是由于潇水段长度占优势，所以潇水应该作为湘江的河流河源。

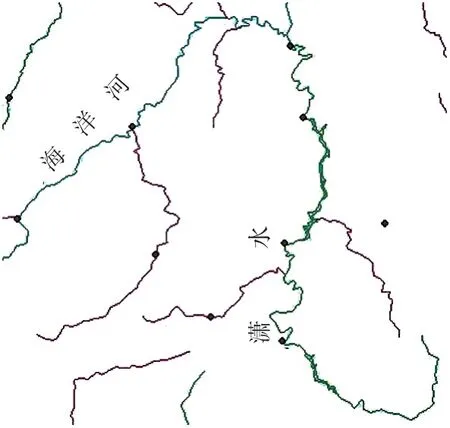
图6 湘江的海洋河和潇水河河段

优先考虑“河源唯长”原则，并结合夹角代表的连通性原则判断我国存在争议的一些河流源头，其结果见表1。

表1 争议河流源头判读结果

5 结 语

运用本文提出的河流河源判断原则对中国东北、华东、中南、中原、西南和西北的数字河流进行了分析，分析结果与权威部门、专家的考察结果基本一致。实验结果说明该方法在河流源头的判断方面具有一定的现实意义。

[1] 毛发新．钱塘江河源的确定[J]．地理研究,1987(1)∶21-30

[2] 石铭鼎．关于长江正源的确定问題[J]．地理研究,1983(1)∶23-34

[3] 冯忠贤,常崇信,樊维翰．汉江河流源头考析[J]．陕西水利,2013(4)∶179-181

[4] 冯利华．河流源头[J]．地球,1993(4)∶2-3

[5] 刘尚仁,叶锦昭,黄泮光．鉴江的河流源头[J]．中山大学学报(自然科学版),1992(1)∶132-136

[6] 税晓洁．长江的起点在哪里?长江到底有多长?[J]．中国三峡建设(人文版),2008(4)∶36-41

[7] ZHOU Qi, LI Zhilin． A Comparative Study of Various Strategies to Concatenate Road Segments into Strokes for Map Generalization[J]．International Journal of Geographical Information Science, 2012 (4)∶691-715

P28

B

1672-4623（2016）09-0023-03

10.3969/j.issn.1672-4623.2016.09.007

宋华标，硕士研究生，主要从事数字地图制图、地理数据处理方面的研究。

2015-07-01。

项目来源：郑州市科技计划资助项目（141PPTGG369）；信息工程大学地理空间信息学院硕士学位论文创新与创优基金资助项目（ZS201503）。