把握试题精髓感悟教学价值

☉浙江省宁波市鄞州实验中学 蔡卫兵

☉浙江省宁波市鄞州区钟公庙中学 朱贤军

把握试题精髓感悟教学价值

☉浙江省宁波市鄞州实验中学 蔡卫兵

☉浙江省宁波市鄞州区钟公庙中学 朱贤军

纵观宁波市近几年的中考数学试卷，不难发现，图形的分割与拼组犹如一棵“常青树”，成为一道靓丽风景，究竟是怎样的情结能让它在试卷中坚守多年呢？我们又怎样看待命题者的这份执着呢？它对我们今后的教学又有什么重要启迪呢？带着这些问题，让我们一起来回眸中考，品味试题.

一、试题呈现

例1（2011年宁波卷第12题）如图1，把四张形状、大小完全相同的小长方形卡片（如图①）不重叠地放在一个底面为长方形（长为mcm，宽为ncm）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分周长和是（）.

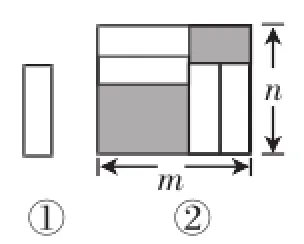
图1

A.4mcm B.4ncmC.2（m+n）cm D.4（m-n）cm

评析：此题图文结合，简洁明了，以矩形纸片为素材，以生成的图形周长为问题核心，具有PISA试题的三个明显特征：情景、运用、思维.将整式的加减、矩形的性质、图形的平移问题融会在基本图形中，主要是将线段进行适当平移，组成新的线段，将未知转化成已知来解决.例2（2013年宁波卷第12题）如图2，7张如图①所示的长为a、宽为b（a＞b）的小长方形纸片，按图②的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示，设左上角与右下角的阴影部分的面积的差为S.当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a、b满足（）.

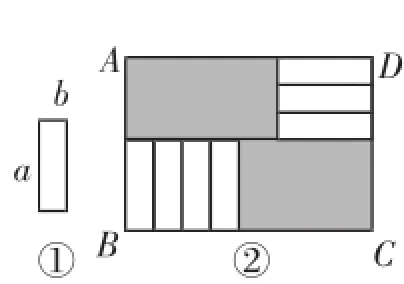
图2

评析：此题考查了整式的混合运算的应用，根据图形和题意，找出各边的等量关系是解答本题的关键.本题在把握“满足条件时，线段AB恰好被该直线平分”这个本质基础上考查学生对数与式的掌握，理解变量与不变量的辩证关系.它蕴含了初中数学中的重要数学思想——整体思想，更多地关注学生的思维能力和创新精神、洞察力，是融PISA理念和初中数学思想于一体的典型范例.

例3（2015年宁波卷第12题）如图3，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（）.

图3

A.①②B.②③C.①③D.①②③

评析：此题考查的内容有数与式、矩形、正方形、中心对称图形的性质和应用，将方程思想、整体思想、数形结合思想、转化思想、平移方法、几何定值融会在基本图形中，在问题解决的过程中考查学生对代数式的变形能力，以及运用图形的变换分析问题的能力，着重考查学生的数学分析能力与数学基本素养.解答此题的关键是要明确中心对称的性质：（1）关于中心对称的两个图形能够完全重合；（2）关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分.

例4（2016年宁波卷第12题）图4是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（）.

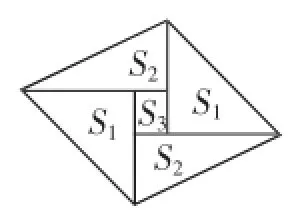
图4

A.4S1B.4S2C.4S2+S3D.3S1+4S3

评析：此题从熟悉的赵爽弦图和平方差公式的几何解释图形的教材背景出发，抓住核心条件进行适当变式，一是将赵爽弦图中的大正方形一般化，将四个全等的直角三角形特殊化，将平方差公式的几何解释图形中的正方形、长方形分割，二是将直角三角形三边关系探究生成整体图形与局部图形面积关系探究，将乘法公式的发现、验证生成运用乘法公式探究面积关系，通过对面积关系的猜想、结论的判断、推理与证明，实现对学生几何直觉、几何推理能力的有效考查.在问题解决的过程中突出考查学生的符号意识、图形变换的方法和归纳探索、逻辑推理、空间想象等各种能力，让学生体会数学的无穷魅力.

二、解法探究

例1解法分析1（凸显符号意识）

设小长方形卡片的长为a，宽为b，再结合图形得出上面的阴影周长为2（n-a+m-a），下面的阴影周长为2（m-2b+n-2b），所以总的阴影周长为2（n-a+m-a）+2（m-2b+ n-2b）=4m+4n-4（a+2b）.因为a+2b=m，所以4m+4n-4（a+ 2b）=4n，故选B.例1解法分析2（运用几何直观）如图5，若将线段AE向上平移至DF，CG向左平移，结果不能完全拼成一个大长方形的长和宽，进而无法求解.但若换位思考，运用转化思想，将AE转化为BG，CF转化为DH，不难发现AE+AH+ CG+CF=BG+AH+CG+DH=BG+CG+AH+DH=2n，从而可得总的阴影周长和为4n，故选B.

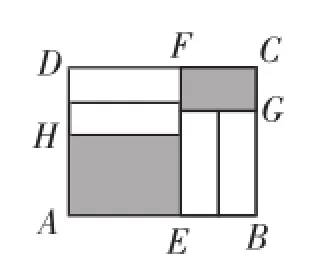
图5

例2解法分析1（凸显符号意识）

设BC=x，则左上角阴影部分的长为AE=x-a，宽为AF=3b，右下角阴影部分的长为PC=x-4b，宽为CG=a.

所以阴影部分面积之差S=AE·AF-PC·CG=3b（x-a）-a（x-4b）=3bx-3ab-ax+4ab=（3b-a）x+ab，则3b-a=0，即a=3b，故选B.

例2解法分析2（运用几何直观）

方法1：如图6，当BC的长度变化时，左上角与右下角的阴影部分的面积的差S始终保持不变，运用转化思想和整体思想可得矩形AFGD与矩形BFGC的面积的差不变，由此发现线段AB恰好被FG垂直平分，所以AF=DG=BF，即3b=a，故选B.

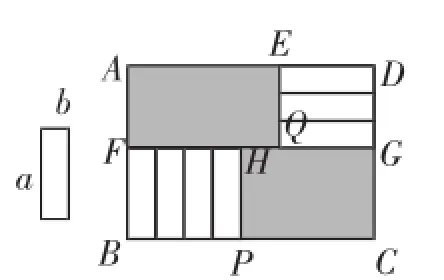
图6

方法2：因为BC是变化的，所以从点P与点C重合开始，然后BC向右伸展，在此过程中左上角与右下角的阴影部分的另一边始终分别为3b和a，另一条边增加的长度相等，增加的面积相等，所以3b=a，故选B.

例3解法分析1（凸显符号意识）

设住房平面图长方形的长为a，宽为b，正方形②的边长为x，正方形③的边长为y.从横向考虑，大长方形的长等于2个正方形②的边长与1个正方形③的边长的和，从纵向考虑，大长方形的宽等于2个正方形②的边长与1个正方形③的边长的差.由这两个等量关系可得关于x、y的方程组解得所以长方形①的周长为2［（x+y）+（x-y）］=4x=a+b，正方形②的周长为4x=a+b，正方形③的周长为4y=2（a-b）.所以当给定大长方形的周长时，标号为①②的图形周长为定值，故选A.

例3解法分析2（运用几何直观）

方法1：如图7，将线段GN平移到DP处，线段PE平移到NB处，即GN=DP，PE=NB.又因为PE=EH+PH=GH+ PH，所以长方形①的周长=CP+NG+GH+PH+CN=CP+ DP+PE+CN=CD+NB+CN=CD+CB.

将线段PH平移到AQ处，线段QF平移到PC处，即PH=AQ，QF=PC.又因为QF=QE+EF=QE+EH，所以正方形②的周长=DP+QE+EH+PH+DQ=DP+PC+DA=DC+DA.所以标号为①②的图形周长均为大长方形的周长的一半，即若只知道原住房平面图长方形的周长，分割后图形①②不用测量就能知道其周长，故选A.

图7

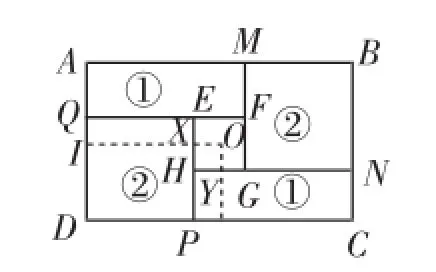
图8

方法2：如图8，过对称中心O沿虚线进行分割，则OX=OY=XH=YH，OI=YN=CD，XP=AD.

所以长方形①的周长=2（HN+HP）=2（HY+YN+HP）=2（HX+HP+YN）=2（XP+YN）=AD+CD；

所以正方形②的周长=2（QE+EP）=2（IX+EX+XP）= 2（IX+OX+XP）=2（OI+XP）=AD+CD.所以标号为①②的图形的周长均为大长方形的周长的一半，即若只知道原住房平面图长方形的周长，分割后①②图形不用测量就能知道其周长.

例4解法分析1（凸显符号意识）

设等腰直角三角形的直角边长为a，正方形边长为b，则S1=a2，S2=（a+b）（a-b）=（a2-b2），S3=b2.

所以平行四边形面积=2S1+2S2+S3=a2+（a2-b2）+b2= 2a2=4S1，故选A.

例4解法分析2（运用几何直观）

方法1：如图9，连接AC、BD、EF，设AC与BD的交点为O.

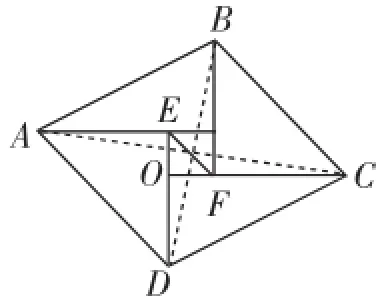
图9

因为四边形ABCD为平行四边形，则OA=OC，OB=OD，平行四边形ABCD的面积=4S△AOD.

易证四边形BFDE为平行四边形，则EF过BD的中点O.

易证EF∥AD，所以S△AOD=S△AED=S1.

所以平行四边形ABCD的面积=4S1，故选A.

方法2：如图10，将两张等腰直角三角形纸片拼成面积为2S1的正方形，另两张直角三角形纸片拼成面积为2S2的矩形.再由图11可知2S2+S3=2S1或由图12可知2S1-S3=2S2，由此平行四边形面积=2S1+2S2+S3=2S1+2S1=4S1，故选A.

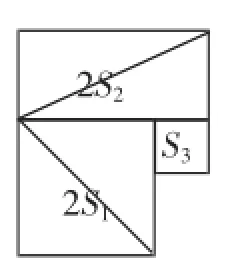
图10

图11

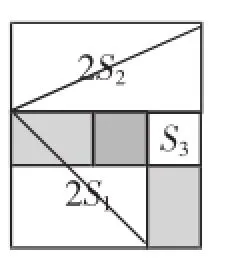
图12

方法3：如图13，将一张等腰直角三角形纸片分割成标号分别为①和②的两部分，将标号为③的直角三角形放置到标号为⑥的位置，将标号为②的直角梯形放置到标号为⑦的位置，将标号为④的正方形放置到标号为⑧的位置，将标号为⑤的等腰直角三角形放置到标号为⑨的位置，由此可知平行四边形ABCD的面积等于等腰直角三角形AFG的面积.因为AF=2AE，所以S△AFG=4S△AED=4S1，所以平行四边形ABCD的面积=4S1，故选A.

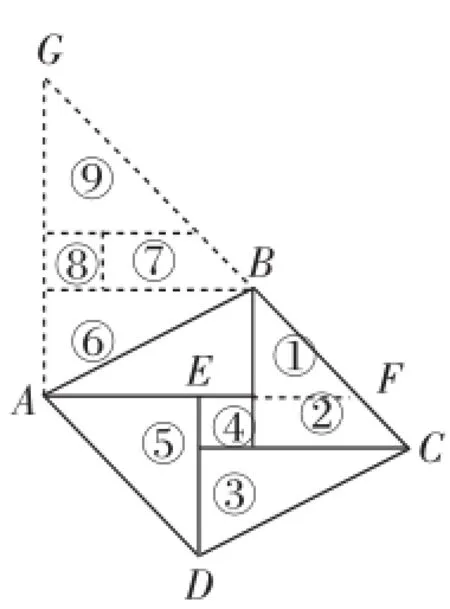
图13

三、试题感悟

1.发展符号意识，培养代数思维

数学的显著特点是形式化、符号化，每一个概念或关系都有确定的符号表示.用字母和符号表示数及其运算或关系是代数学的一个基本特征.数学符号既是数学的语言，也是数学的工具，更是数学的方法，它具有抽象性、明确性、可操作性的特点，还具有简略性和通用性等特点，它反映了表达意义的内在结构和逻辑关系，成为表达特定思想的载体和诱导思维的刺激物.例1中小长方形卡片的长和宽的符号化a、b方便表示上面的阴影周长为2（n-a+m-a）、下面的阴影周长为2（m-2b+n-2b）、总的阴影周长为4m+4n-4（a+2b）和清楚说明相关线段之间的内在关系a+2b=m；例2中线段BC长度的符号化x方便表示上面的阴影面积为3b（x-a）、下面的阴影面积为a（x-4b）、面积之差为（3b-a）x+ab和清楚说明常数函数S与自变量x的无关性；例3中住房平面图长方形的长和宽、正方形②③的边长的符号化a、b、x、y清楚说明横纵向各线段之间的主要关系2x+y=a、2x-y=b和方便表示长方形①②③的周长分别为a+b、a+b、2（a-b）；例4中等腰直角三角形的直角边长、正方形边长的符号化a、b方便表示平行四边形面积2a2和清楚说明面积之间的内在关系2S1-2S2=S3.实施符号化，即用字母表示相关线段的长，再用符号进行相关线段的数学表达、运算和推理.主动选择相关线段“用字母表示线段长”是培养符号意识的可操作途径，使用符号去构建代数式、方程、函数模型后进行数学思考和问题解决，感知符号的意义，培养符号意识，深化符号的运用，将解决具体问题的思维操作转化为对符号的操作，有利于增强学生建立数学模型的意识，提高解决实际问题的能力，培养学生的数学语言表达能力，进一步深化符号感.

2.运用几何直观，展示数学魅力

几何直观就是依托利用图形进行数学的思考与想象，可以理解为借助见到的或想到的图形的形象关系形成对数量关系的直接感知，从而利用图形描述和分析问题.借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果.上述四例突出了“数”与“形”的有机联系，彰显了美和真的和谐统一.例1中运用线段的平移和等量代换将两条不在同一直线上的未知线段AE、CG（CF、AH）转移到同一直线上的首尾相接的两条线段BG、CG（DH、AH），由此利用整体思想进一步转化为长度为n的已知线段BC（AD）；例2中运用图形的运动和图形的组合将左上角与右下角的阴影部分的面积差的不变性转化为面积变化量相等问题，由此借助图形进一步转化为图形的边长AF、BF相等（即3b=a）；例3中运用图形的分割和线段平移实现线段和CP+NG+GH+PH+CN的有效组合CD+CB；例4中运用图形的位置关系实现等积转化（S△AOD=S△AED），利用图形的拼组割补实现图形的重组（图10或图13）.以图形为核心，以问题为支撑，以思考为导向，形成一种认识事物的能力——几何直观，使抽象的问题直观化，让学生更容易地了解其内在的性质和规律.善于发现图形中的结构特征，从中抽取出数量、形状、位置、变换等关系，使之呈现“标准”或“熟悉”的状态，顺利实现模型化归，释放问题内涵，创造性地使用图形解决问题，挖掘新思路，寻求新方法，使数学逻辑和数学直观相互交织，直观中有逻辑，逻辑中有直观.

3.渗透数学思想，提升核心素养

《全日制义务教育数学课程标准（修定稿）》强调了数学素养是现代社会每一个公民应具备的基本素养，数学思想方法是解决数学问题的指导思想和重要策略，是体现学生素养、数学学习的灵魂.重视加强对学生进行数学思想方法的渗透，不但有利于提高课堂教学效率，而且有利于提高学生的数学核心素养和思维能力.上述四例将整体思想、转化思想、方程思想、函数思想、数形结合思想和平移方法融会在基本图形中，更多地关注学生的思维能力和创新精神、洞察力.比如，在例3解析时先让学生有自己的切身体验，逐步领悟大长方形的任意性、满足要求的分割的存在性和唯一性及可操作性，体验特殊的数量关系与位置关系沟通与关联的转化思想和整体思想，体验用字母表示图中有关线段的长度体现的符号意识和数形结合思想，通过方程思想进行数式的运算是进行数学思考和表达的重要形式，相互“释译”——让解题信息在文本与图形中获取，广泛联系——让解题方法在关联与融合中形成，合理渗透——让思想方法在启发与探究中升华，一题多解——让创新意识在求解与比较中发展.数学思想方法比数学知识更抽象，思想方法的教学是一种数学活动的过程，重在领会应用，学生的参与显得尤其重要，需要让学习者在长期的学习过程中尽可能多地领悟其中的真谛，用自己的思维方式构建数学思想方法的体系，当经验和领悟积累到一定程度时，数学方法就会凸显出来.在教学中有意识、有效地加以渗透，让学生在潜移默化中领悟、运用，并逐步内化为数学思维品质，进而提升学生的数学素养.

1.赵军.三年坚守与思变［J］.中学数学教学参考（中），2012（10）.

2.李洪芹.培养学生“符号意识”的途径之一——用字母表示线段长［J］.中学数学（下），2013（10）.

3.苑建广.对几何直观教学的思考［J］.中国数学教育（初中版），2014（5）.Z