基于基金组织模式的生物质燃料供给研究
檀勤良,邓艳明,赵建英,魏咏梅,张兴平
(1.华北电力大学,北京 102206;2.北京能源发展研究基地,北京 102206;3.山西省委党校,山西 太原 030006)
基于基金组织模式的生物质燃料供给研究
檀勤良1,2,邓艳明1,赵建英3,魏咏梅1,张兴平1
(1.华北电力大学,北京 102206;2.北京能源发展研究基地,北京 102206;3.山西省委党校,山西 太原 030006)
生物质燃料收集难是制约生物质发电产业发展的主要因素之一,生物质燃料供给模式对生物质发电产业的发展有着重要作用。本文建立传统模式下经济效益最大化的农户、经济组织、电厂三者的动态博弈模型;并引入基金组织,即村委会组织农户收集燃料,销售收入部分归农户,部分用于村基础设施建设,构建考虑效用最大化的农户、基金组织、电厂三方的博弈模型。结果表明,农户生物质燃料供给量、组织提供给农户的价格同上网电价呈正相关关系,同燃料的运输、存储及预处理成本呈负相关关系。另外,基金组织模式下,效用函数系数对生物质燃料供给量和基金组织给农户的经济利益有一定影响。对两模式进行比较发现,基金组织模式下,农户的生物质燃料供给量和收益均高于传统模式。政府实施激励后农户的效用、组织的效用、电厂的经济利益均增加。
生物质能;基金组织模式;燃料供应模式;纳什均衡
1 引言
生物质能是目前世界上应用最广泛的可再生能源,其消费量仅次于煤炭、石油和天然气,生物质发电为生物质能开发利用的主要方式之一,已成为世界的热门话题。我国生物质能源丰富、开发潜力巨大,但目前我国生物质发电产业发展缓慢,生物质燃料收集困难是制约生物质发电产业发展的主要因素。为解决生物质发电燃料收集难的问题,国内外学者对生物质发电燃料供给模式进行了大量研究。总的来说,生物质燃料供应主要有三种模式:“农户+电厂+政府”模式、“农户+中间商+电厂+政府”模式、和“农户+中间商+第三方物流+电厂+政府”模式。其中农户负责收集生物质资源,中间商负责生物质燃料的收购、预处理、储存等工作,第三方物流负责燃料的运输,政府则从政策层面给予鼓励和支持。
在不同的模式下,利益群体之间的利益共享机制、政府政策支持等都是关系到生物质发电燃料供应的关键问题。Junginger等[1]以泰国为例,在对发展中国家的大规模生物质发电原材料供应策略研究的基础上,提出一种降低原料供应风险的方法。Nasiri等[2]建立了分销商、农户和设施开发者三者之间的序贯博弈模型,并探讨了激励对博弈模型的影响。魏巧云[3]针对生物质秸秆燃料供给各阶段的影响因素进行了调研,并分析了不同收集模式下成本的变化。van Dyken[4]针对电热系统,设计了生物质供应链中的供应、加工处理、储存以及对不同生物质需求的混合整数规划模型。徐云海[5]运用博弈理论建立发电厂与农民之间的博弈模型,构建了秸秆收购管理体系。何亮运[6]用覆盖模型和P-中值模型将秸秆收集模式和秸秆资源定价结合起来进行研究。刑爱华等[7]结合秸秆类生物质资源的岛式分布特点,在考虑秸秆收集过程成本、能耗和污染物排放等因素的基础上,建立数学模型并进行了敏感性分析。张永等[8]运用系统动力学原理对生物质能供应链的运作进行模拟,建立政府、企业和农民协调关系的动态反馈模型。王晓凌[9]以河南省为例,从农户行为角度出发对生物质能的利用情况进行分析,并建议构建“企业+合作社+农户”的生物质能产业化合作模式。钱志新和唐高哲[10]结合我国生物质电厂的实际情况,引入集成化供应链理论和价值分析理论,建立了生物质集成化供应链系统,协调优化供应、配送、生产等各环节,从而最大限度改进供应链。张卫东等[11-13]建立三方动态价格博弈模型并得到序贯博弈的纳什均衡。相方龙等[14]对农户、电厂和政府行为建立三者之间的重复博弈模型,得出纯策略的纳什均衡,探讨了政府在供应链中的影响,并对电厂和政府给出了积极性建议。
这些研究成果均认为生物质燃料供给的主体均追求经济利益最大化。翟丽丽等[15-16]从有限理性对博弈模型进行了研究。本研究小组对农户秸秆的供给行为进行了深入的分析,研究结果表明非价格因素对农户的秸秆供给行为具有显著的影响[17]。基于此,本文拟在传统模式和基金组织模式下分析生物质供应链各利益主体的行为,构建基于经济效益最大化和效用最大化的两种完全信息动态博弈模型,通过比较,分析不同生物质燃料供应模式的特点。
2 基于传统模式的博弈分析
2.1 模型构建
传统模式下,行为主体均追求经济利益最大化,生物质燃料收集的组织为经济组织,考虑经济利益最大化,典型代表有“经纪人”、中间商或第三方物流,农户为完全理性人,追求个人利益最大化。构建经济组织、农户和电厂三方的完全信息动态博弈模型对供给模式进行探讨。该种情况下,各方的收益函数为:
(1)
max πo=(pe-p0)q-c1q
(2)
max πe=(pu-cc)rq-peq-c2q
(3)
其中,πf、πo、πe分别为农户、经济组织和电厂的经济收入;pm为生物质燃料的市场价格(元/吨),pe为电厂向经济组织收购生物质燃料的价格,p0为经济组织提供给农户的燃料价格,pu为生物质电厂发电的上网电价(元/kWh),且pe>po>pm;cq农户供应生物质燃料的单位生产操作成本(元/吨);q代表生物质燃料的收购数量(吨);αe为电厂对经济组织的激励系数;ct表示组织运输单位产量单位距离燃料的成本;cs组织存储单位产量燃料的成本;ct′电厂运输单位产量燃料的成本;cs′电厂存储单位产量燃料的成本;cd电厂处理单位产量燃料的成本;cc单位发电的变动成本;r生物质燃料发电的转化率;l生物质燃料从收购点到电厂的平均运输距离;c1表示组织运输和存储单位燃料的成本;c2表示电厂存储、运输及预处理单位燃料的成本。假设:
(4)
pe=(1+αe)po
(5)
2.2 纳什均衡的求解
用逆向求解法对博弈模型进行求解,将公式(4)、(5)代入(1),可得到农户生物质燃料供给的最优量为:
(6)
由(6)知,农户的生物质燃料供给量同经济组织给农户的价格水平呈正比例,同自身的收集操作成本呈反比例关系,当分配价格为零时,农户没有供给行为。将(6)代入公式(2)得:
(7)
由式(7)知,经济组织给农户的价格同电厂对经济组织的价格激励水平呈正相关关系,同组织的收集、存储成本呈负相关关系。电厂应给予经济组织适当的激励,保证经济组织和农户能够有一定的盈利空间,否则当激励不足以弥补组织成本时,组织将不再积极的进行收购。将式(7)代入(3)可得:
(8)
当上网电价高于一定水平,电厂对经济组织的激励水平同生物质燃料的市场价格、电厂的运输、存储和预处理费用呈负相关关系;同上网电价、组织的运输和存储成本呈正相关关系。即:随着上网电价上升和组织运输及存储成本的增加,发电厂对组织的激励水平会提高;反之,当生物质燃料的市场价格、电厂运输、存储和预处理成本较高时,电厂对组织的激励水平将降低。而当电厂的上网电价低于某一水平时,电厂对经济组织的激励也将下降到某一值或以低于市场水平的价格进行燃料的收购。
由公式(6)、(7)、(8)可以得到农户、经济组织和电厂三方博弈的纳什均衡解,即:
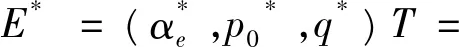
(9)
E1*=(αe1*,p01*,q1*)T=
(10)
E2*=(αe2*,p02*,q2*)T=
(11)
式(10)、(11)为三方博弈的纳什均衡,根据E1*可知:农户生物质燃料供给量、经济组织给农户的价格同上网电价呈正相关关系,同电厂和组织的运输、存储及预处理成本呈负相关关系;即上网电价越高,农户的供给积极性越高,收集的生物质燃料量越多。由E2*知,当上网电价在一定范围内,电厂对组织的激励水平将不发生变化,农户供给量、组织给予农户的价格将与电厂的运输、存储及预处理成本呈负相关。
3 基于基金组织模式的博弈分析
3.1 农户、基金组织和电厂三方完全信息动态博弈
随着经济的发展和社会的进步,农户并不单纯追求经济利益最大化,而会关注一些非经济性因素,比如农村基础设施建设、环境保护等[18]。农村基层组织(比如村委会)为农村资源整合的重要载体,其行为对农户个体行为有着显著的导向作用,能够促进村庄的团结和发展。因此本文假设存在由村组织牵头成立的基金组织来组织农户进行生物质燃料的收集和销售,其销售收入的一部分归参与基金组织的农户所有,另一部分留作村委会的公益基金,对村庄的基础设施进行建设和完善,本文称之为“基金组织”模式。在此模式下,农户和基金组织追求效用最大化。进而构造考虑农户、基金组织效用最大化和电厂经济效益最大化的博弈模型,其中农户的效用由绝对收益和相对收益的对数函数组成,基金组织的效用由其经济利益和环境效益的对数函数组成。环境效益的研究中,生物质能的环境效益主要体现在节煤、减排、资源利用、地面改善、收集量等方面[20-22],均是生物质能量的直接或间接折算,因此本文选取销售量来代表环境效益。具体如下:
(12)
max uo=Dln[pe′q-p0′q-c1q]+Elnq
(13)
max πe=(pu-cc)rq-pe′q-c2q
(14)
其中,uf表示农户的效用;A、B分别表示农户的绝对收益和相对收益的效用系数,其大小同农户的特性有关;uo表示基金组织的效用,D、E分别代表经济效益效用和环境效益效用的系数水平;p0′表示基金组织分配给参与组织进行燃料销售的农户的价格水平;pe′为电厂向基金组织收购生物质燃料的价格;αe′为电厂对基金组织的激励系数。
pe′=(1+αe′)pm
(15)
用逆向求解法求解该博弈模型的纳什均衡。将公式(4)、(15)代入公式(12)可得,最优生物质燃料供给量为:
(16)
由式(16)知,在基金组织模式下,农户的生物质燃料供给量同农户的操作成本和相对收益效用系数呈负相关关系,同基金组织提供的价格水平和绝对收益效用系数呈正相关关系。即:绝对效益在总效用中贡献度越大、组织提供给农户的分配价格越高,农户参与组织进行燃料供给的积极性越高,供给量越大。将式(16)代入公式(13)中可得:
(17)
由(17)知,基金组织给农户的分配价格同电厂对组织的激励水平和环境效用系数呈正相关关系,同组织的收集、运输成本和经济效益效用系数成负相关关系;在其它条件一定时,环境效用对基金组织总效用的作用越大,组织分配给农户的价格水平就越高。将(17)代入公式(14)可得:
(18)
由式(18)知,电厂对基金组织的激励水平并未随运营模式的改变而改变。由(16)、(17)、(18)可知,基金组织模式下考虑效用最大化博弈模型的纳什均衡解为:
E**=(αe′**,p′**,q**)T=
(19)
(20)
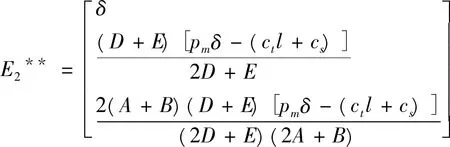
(21)
式(20)、(21)为基金组织模式下考虑基金组织、农户效用最大化及电厂经济利益最大化博弈模型的纳什均衡。同传统模式下的纳什均衡相比,该均衡中农户的生物质燃料供给量和组织给农户的价格还受效用系数的影响。
3.2 两种供给模式的比较
农户是否供给是生物质燃料收集的关键,对基金组织模式和传统模式下农户的收益进行比较,基金组织模式下农户的绝对收益和相对收益分别为πf1′、πf2′,传统模式下农户的收益为πf;其中
(22)
(23)
对(22)、(23)比较知:πf′>πf,基金组织模式下,农户收益较高,农户更倾向于参与村组织牵头成立的基金组织进行燃料的收集和销售。
通过两种模式的比较还发现,q* 假设政府根据生物质燃料的市场价格,对供给生物质燃料的基金组织给予适当的激励,其激励价格系数用αg表示,在该情况下,农户和基金组织的效用函数均有所变化。 (24) max uo=Dln[pe′q-p0′q-c1q+αgpmq]+Elnq (25) 用逆向求解法对(14)、(24)、(25)构成的博弈模型进行求解,得; (26) (27) (28) (29) 进一步计算政府激励后纳什均衡的变化,激励前E**=(αe′**,po′**,q**)T,则激励后的纳什均衡为: (30) 激励后,电厂对基金组织的激励水平下降,而农户燃料供给量和组织给予农户的价格均增大,进一步对各方利益变化进行比较。激励前各方效用及收益为:uf*、uo*、πe*,激励后为:uf**、uo**、πe**。 (31) (32) (33) 通过式(31)、(32)、(33)的比较可知: (34) 根据比较结果(34)可知,政府对基金组织实施激励后,农户的效用、组织的效用、电厂的经济利益均显著增加。另外,政府对基金组织实施激励后,农户的生物质燃料供给量增加, 农户的供给行为明显加强。在基金组织模式下,政府给予基金组织一定的激励能促进基金组织模式的健康发展,进而促进生物质发电产业的发展。 表1 相关数据表 表2 纳什均衡结果 本文以某生物质发电厂为对象,该电厂年发电时间达350天,上网电量为8400万kW·h,对生物质秸秆燃料供应环节进行实地调研,结合实地调研得到相关数据如表1。 将上述数据代入公式(10)、(20)、(22)、(23)、(29)设A、B、D、E均为1得到结果,如表2。 在实地调研中发现,pe=250元/t,p0=100元/t,由表2知,纳什均衡得到:pe=264.8元/t,p0=97.4元/t,鉴于不确定因素的影响,实际收集价格同传统模式纳什均衡有微小偏差,但基本符合传统模式。另外,基金模式下,组织提供给农户的生物质燃料价格、农户供给量、农户收益及电厂收益均高于传统模式,说明基金组织模式下,农户供给生物质燃料的积极性更高,利于生物质燃料的收集。 政府对基金组织模式进行激励,发现αe变小,p0、q、uf、πe均增大,说明政府对基金组织模式加以激励能够促进该模式的发展,且农户效用、电厂收益同激励水平呈正相关关系。农户的供给量也随着激励水平的增加而加大,政府在实施激励时,可适当采取阶梯型激励措施,以供给量为界,对不同区间的供给量水平给予不同的激励,最大限度调动农户及组织积极性的同时,尽量减少政府不必要的开支。 本文首先在传统模式下,建立农户、经济组织和电厂三方经济利益最大化的完全信息动态博弈模型。然后在基金组织模式下,构建农户、基金组织效用最大化和电厂经济利益最大化的完全信息动态博弈模型。两博弈模型的纳什均衡结果均显示农户的生物质燃料供给量、组织提供给农户的价格同上网电价呈正相关关系,同电厂和组织的运输、存储及预处理成本呈负相关关系。另外在基金组织模式下,效用函数系数对供给量和基金组织给农户价格有一定的影响,且相对收益效用和环境效用对农户的决策行为影响较大。通过两种模式的比较发现,基金组织模式下,农户的收益和生物质燃料供给量明显高于经济组织模式,农户供给积极性较高。因此,基金组织运营模式较适合生物质发电燃料的收集,能够在一定程度上促进生物质发电产业的发展。且政府对基金组织实施激励后,各行为主体的收益均有所提升,能对基金组织模式加以巩固。 基金组织模式能够提高农户对生物质燃料供给的积极性,增加生物质燃料的供给量,能有效促进生物质发电产业的发展。因此,政府应鼓励村委会等基层组织成立相应的基金组织,进行燃料的收集、供应,并根据生物质燃料的供给量给予适当阶梯型补贴,以促进基金模式发展,并进一步提高农户供给积极性。 [1] Junginger M, Faaij A, Van den Broek R, et al. Fuel supply strategies for large-scale bio-energy projects in developing countries. Electricity generation from agricultural and forest residues in Northeastern Thailand[J]. Biomass and Bioenergy, 2001, 21(4): 259-275. [2] Nasiri F, Zaccour G. An exploratory game-theoretic analysis of biomass electricity generation supply chain[J]. Energy Policy, 2009, 37(11): 4514-4522. [3] 魏巧云.生物质发电秸秆供应链物流成本研究[D].北京:中国农业大学,2014. [4] van Dyken S, Bakken B H, Skjelbred H I. Linear mixed-integer models for biomass supply chains with transport, storage and processing[J]. Energy, 2010, 35(3): 1338-1350. [5] 徐云海.德源九台生物热电厂秸秆收购体系的研究分析[D].北京:华北电力大学,2007. [6] 何亮.生物质能源资源可供性评价及实证研究[D].太原:山西财经大学,2008. [7] 邢爱华,刘罡,王垚,等.生物质资源收集过程成本,能耗及环境影响分析[J].过程工程学报,2008,8(2): 305-313. [8] 张永,陈晓娇,景月明.生物质能供应链协调机制研究[J].物流技术,2009,28(3):58-63. [9] 王晓凌.我国生物质能开发利用中的农户行为研究[D].北京:中国农业科学院,2009. [10] 钱志新,唐高哲.生物质电厂集成化供应链系统研究[J].现代管理科学,2010,(06):5-7. [11] 张卫东,耿笑.基于三方博弈模型的网络交易平台收费机制研究[J].中国管理科学, 2014, 22(12): 135-141. [12] 王燕,沈辉.生物质发电供应链的完全信息动态博弈[J].价值工程,2010,29(19):41-42. [13] 王燕.博弈论情况下的生物质发电供应链合作模式研究[D].南京:南京航空航天大学,2011. [14] 相方龙.基于MAS的生物质能供应链博弈分析[D].青岛:青岛大学,2011. [15] 翟丽丽,柳玉凤.软件产业虚拟群体企业间信任进化博弈研究[J].中国管理科学,2014,22(12):118-125. [16] 张乐,王慧敏.突发水灾害应急合作的行为博弈模型研究[J].中国管理科学,2014,22(4):92-97. [17] 檀勤良,邓艳明,张兴平,等.农业秸秆综合利用中农户意愿和行为研究[J].兰州大学学报,2014,42(5):105-111. [18] 张国兴,张绪涛.节能减排补贴政策下的企业与政府信号博弈模型[J].中国管理科学,2013,21(4):129-136. [19] 蔡树文. 生物质发电效益评估及对策研究[J].纵横经济,2007,(01):23-25. [20] 樊超,司慧.北京市生物质能源利用效益评价方法研究[J].中国农学通报,2012,28(26):190-195. [21] 何璇.新疆农业生物质能资源利用的综合效益分析[D].新疆:新疆农业大学,2014. Research on the Biomass Fuel Supply Based on Foundation Organization Pattern TAN Qin-liang1,2, DENG Yan-ming1, ZHAO Jian-ying3, WEI Yong-mei1, ZHANG Xing-ping1 (1.North China Electric Power University, Beijing 102206, China;2.Research Center For Beijing Energy Development, Beijing 102206,China;3.Shanxi Provincial Party School, Taiyuan 030006,China) It is very difficult to collect biofuel, which is a main constraint of developing the biomass generation industry. Biofuel collecting mode plays a significant role in promoting the biomass power industry. In this paper, two dynamic game theory models are built: (1) Optimizing the economic benefits of farmer, economic organization and biomass power plant under tradition mode; (2) maximizing the utilities of these three parties with introduction of foundation organization, i.e. the village committee organizes the farmers to collect the biomass feedstock, part of whose revenue belongs to the farmers and the rest is utilized for the village’s infrastructure construction. The income is divided to two parts; one owes to farmers, the other is used for building infrastructure. The results demonstrate that the supply amount of biomass fuels and the price offered by organizations to the peasants have positive correlation relationship with feed-in tariff, while negative correlation with the cost of biomass fuels transportation, storage, and preprocess. Moreover, in the mode of foundation organization, the coefficient of the utility function has impact to some extent on the supply amount of biomass fuels and the benefit to peasants delivered by foundation. The biomass fuels supply amount and the peasant’s income in the foundation organization mode are higher than those in the tradition mode. With the incentives from government, the utilities of the farmer and organization present significant, as well as the economic benefit of biomass power plant,increase. biomass energy; foundation organization pattern; biofuel supply mode; Nash equilibrium 2014-11-19; 2015-06-29 国家自然科学基金资助项目(71373077);国家社科基金重大项目(15ZDB165);北京市共建项目(GJ2013012) 简介:檀勤良(1969-),男(汉族),福建福州人,华北电力大学教授、博士,研究方向:能源环境建模与优化,E-mail:tql@ncepu.edu.cn. C934 A 1003-207(2016)09-0099-07 10.16381/j.cnki.issn1003-207x.2016.09.0124 政府激励对基金组织模式下纳什均衡的 影响
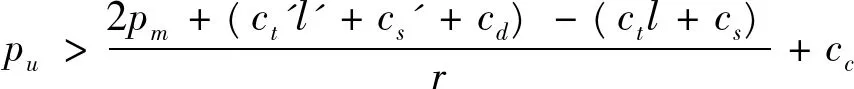
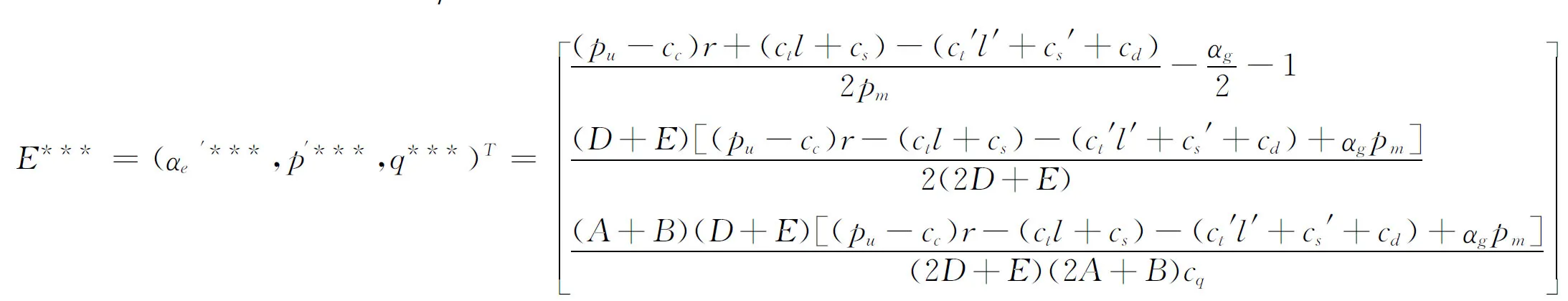


5 算例
6 结语

