抗差自适应Kalman滤波模型的可行性分析

熊文全，胡家兴

（1.国家测绘地理信息局 重庆测绘院，重庆 400015）

抗差自适应Kalman滤波模型的可行性分析

熊文全1，胡家兴1

（1.国家测绘地理信息局 重庆测绘院，重庆 400015）

将抗差估计原理引入到经典Kalman滤波（CKF）方法中，即抗差自适应Kalman滤波（RAKF），在抑制观测粗差及状态扰动方面，存在明显的优势。通过大坝变形监测实例说明，在变形监测数据处理中RAKF比CKF解算结果更可靠有效。RAKF在抑制状态预报粗差及观测粗差方面的优势是显而易见的，是一种可行的有效估值方法。

CKF；RAKF；自适应因子；可行性

Kalman滤波在测量数据处理，特别是在工程变形和地壳变形、动态数据处理与GPS定位定轨等方面的应用广泛[1]。CKF是一种高效滤波，但容易受观测样本和参数预报值质量的影响，抗差Kalman滤波能有效解决各种因观测值或参数预报值的质量问题而引起的参数解不可靠问题，可有效减小观测值随机噪声；但其可靠性必须以重复迭代计算为代价[2-3]。而自适应Kalman滤波可以较好地减小状态预报值的随机误差[4-5]。将二者的优势结合起来，采用RAKF，从理论上可以得到更加可靠的结果。

本文首先介绍了RAKF的基本原理，再通过实例说明了它在抑制观测粗差及状态扰动方面存在的明显优势，并在数据滤波估计方面比CKF值更可靠有效。当系统状态预报值或观测值存在粗差，或二者同时存在时，RAKF能有效抑制它们所带来的不良影响。

1 RAKF

式中，LK为观测向量；AK为设计矩阵；VK为残差向量，其协方差矩阵为QK；XK为状态参数向量；XK-1为K-1历元的状态向量，其估计值为K-1，K-1的残差向量为；WK-1为状态方程误差向量，相应协方差阵为QWK-1；ΦK,K-1为状态转移矩阵。假设在K时刻增加新观测LK，K-1历元的状态XK-1的滤波值为K-1，相应观测误差方程和状态误差方程分别为：

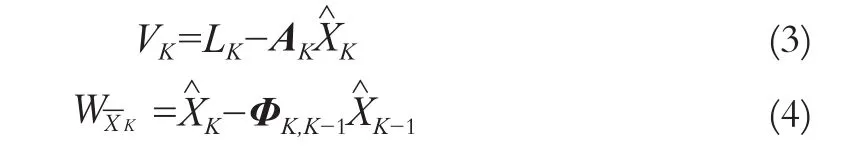
抗差自适应滤波的基本原则为：

式中，αK为自适应因子；为观测量L的抗K差等价权，它是观测向量权矩阵的自适应估值；PXK为的权矩阵[6]。则抗差自适应滤波的解为：

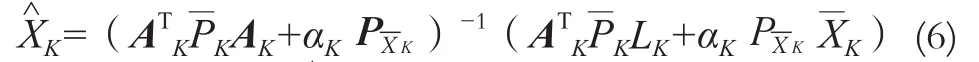
则上述抗差自适应滤波解可表示成式（7）的形式。其中增益矩阵和滤波方差分别为：

可知，当α=1，RAKF就是经典的抗差Kalman滤波。

对于其预测值的精度可采用式（10）进行[1,6]：

2 自适应因子α的确定

自适应因子α由观测信息与状态预测信息不符值确定，具有实时自适应功能。它作用于预测状态向量K的协方差矩阵，主要对状态不符值或状态扰动进行自适应修正，以达到抵抗状态误差的扰动效果[7-9]。自适应因子一般取值在0至1之间。因此假设K时刻状态参数的真值为XK，则与一步预测值K之差为[8,10]：

但是，一般状态参数的真值是无法知道的，因此这里取由K时刻观测值直接求解出的抗差解近似代替其真值，其中为抗差等价权。则式（14）可写成：

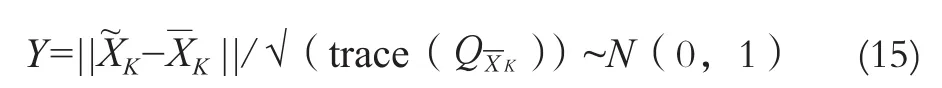
当抗差解与一步预测值相同时，Y为零，即近似认为系统不存在扰动或系统扰动很小，其对滤波值精度影响可忽略不计。当Y值越小，即由观测值求出的抗差解与一步预测值越接近，从数学期望的角度来说，一步预测值的期望值更加接近由观测值直接求出的抗差解。

因此，可以采用M估计中的Huber函数来确定自适应因子的取值，其具体公式如下：

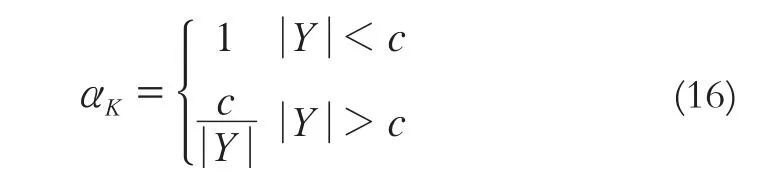
式中，c一般取1.5～2。当Y值越大，其对应的自适应因子越小，从而降低其所对应的状态参数权值，达到抵抗系统可能存在的粗差的目的，并抑制状态预报误差对滤波值的影响。

3 实例分析

某大坝上布设了5个水平变形监测点，2012年初对其进行了近一个月的连续水平变形监测，观测值为等时间间隔（1 d）。现将其中一点（P4点）28期的水平径向原始观测值列于表1[11]，对此进行CKF处理和RAKF处理，其中状态参数的初始值由前两期的观测结果确定，从第2期开始进行滤波处理。

1）大坝动态变形监测系统的Kalman滤波数学模型的建立。由于在构筑物的变形监测中，系统一般是定常的，且动力模型噪声WK和观察噪声V 一般都是平稳随机序列，故ΦK.K-1、AK、QWK-1和QK都是常阵。

设观测点的状态向量为XK=[X，λ]T，其中X为径向观测值；λ为观测点的径向变动速率，由式（1）、（2）得状态方程和观测方程，其转移矩阵及系数矩阵分别为：

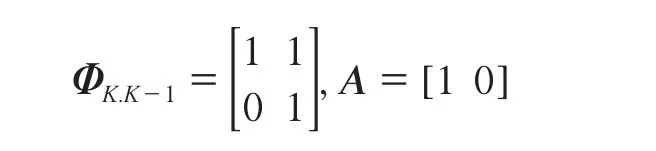
3）Kalman滤波分析。CKF与RAKF进行预报及滤波后预报残差、滤波残差及其相应精度见图1。

表1 P4点28期水平径向原始观测值/mm

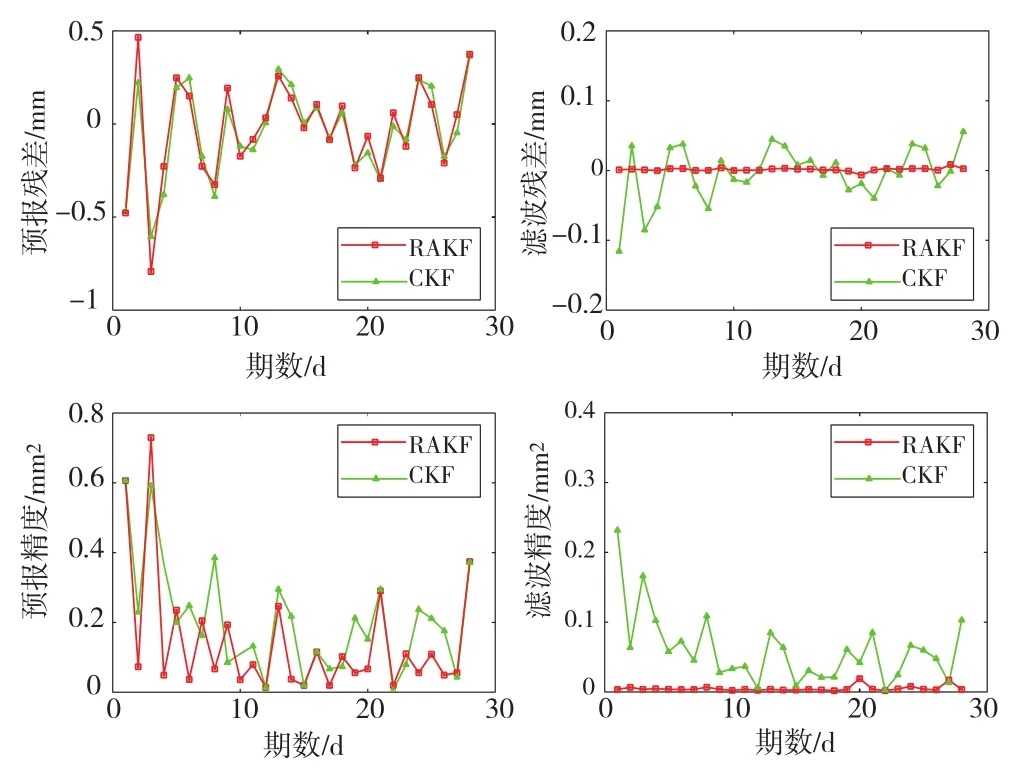
图1 无粗差时RAKF与CKF预报及滤波比较

从图1可知，当观测值及状态预报值不存在粗差的前提下，CKF和RAKF滤波在进行状态预报及滤波时，无论从预报残差和预报精度，还是从滤波残差和滤波精度上，RAKF总体上明显优于CKF。因此，RAKF滤波在进行变形监测数据处理与预报时，只要数学模型建立合理，滤波值与预报值都明显优于CKF，并能足够满足工程要求。

RAKF在抑制状态预报粗差及观测粗差对预报值和滤波值的影响方面，本文采用3种方案进行分析。

方案1：对滤波状态初始值加入粗差，即在第1次初始值预报时，人为加入了5 mm的误差，即X0=[92.69 mm，0.47 mm/d]，对P4点的28期数据分别进行CKF和RAKF处理，得到的预报值和滤波值分别与原始观测值作差，得到相应的残差图及精度见图2。

方案2：对P4点的28期原始观测数据中第3期和第8期分别加入3 mm和5 mm的粗差，分别进行CKF和RAKF处理，得到的预报值和滤波值分别与原始观测值作差，得到相应的残差图及精度见图3。

方案3：对滤波状态初始值加入粗差5 mm的同时，并对P4点的28期原始观测数据中第3期和第8期分别加入3 mm和5 mm的粗差，即方案1与方案2的叠加，然后分别进行CKF和RAKF处理，得到的预报值和滤波值分别与原始观测值作差，得到相应的残差图及精度见图4。

图2 状态初始预测存在粗差时RAKF 与CKF预报及滤波比较

图3 观测值存在粗差时RAKF 与CKF预报及滤波比较

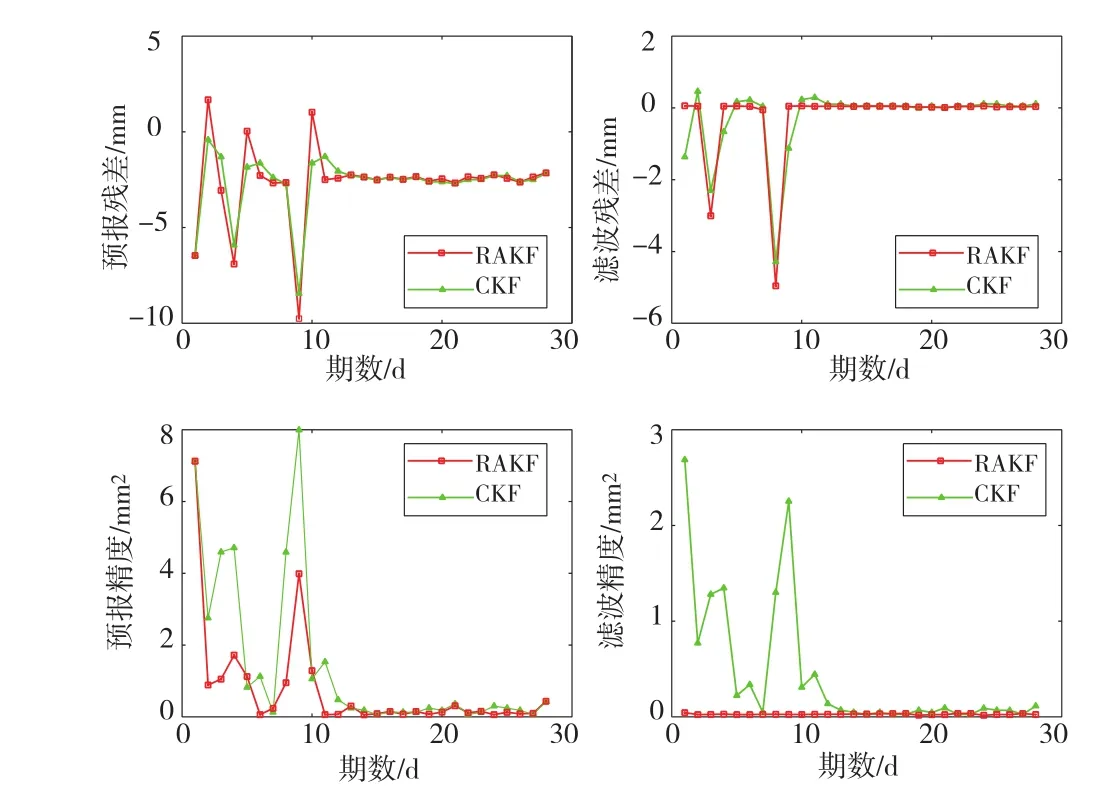
图4 观测值及状态初始值都存在粗差时RAKF与CKF预报及滤波比较

由图2可知，当预报存在粗差时，RAKF预报结果更能反映粗差存在的点位，且预报精度优于CKF，在抑制状态预报粗差对滤波带来不良影响效果方面，无论从滤波值还是精度方面，RAKF都明显优于CKF；由图3、图4可知，无论是方案2还是方案3，在预报方面，RAKF与CKF预报结果相当，在粗差点反映和预报精度上，RAKF优于CKF，而在滤波方面，RAKF能够很好凸显粗差点位置，且能够很好地抑制观测粗差及状态预报粗差对后期滤波的不良影响。无论是滤波结果还是精度，RAKF都总体明显优于CKF。

4 结 语

本文从RAKF基本理论出发，通过某大坝变形监测实例，在正确确定初始状态模型值后，用CKF和RAKF同时进行了数据处理，得出的结果是当系统不存在粗差或不存在微小扰动时，无论是预报还是滤波及其相关精度方面，RAKF总体上明显优于CKF，其滤波值与预报值都能满足工程的要求。对RAKF在抑制状态预报粗差及观测粗差所带来的影响方面作了进一步的分析，从实验数据分析来看，当系统存在粗差或微小扰动时，RAKF在抑制状态预报粗差及观测粗差对滤波值影响方面效果是显著的，是对CKF滤波的一种改进，同时，随着滤波时间的增长，逐渐趋于平稳。因此，在进行变形监测数据处理与分析时，无论是在预报结果、滤波结果还是其精度方面，RAKF比CKF更可靠有效，是一种可行的有效估值方法。

[1] 陶本藻.Kalman滤波模型误差的识别[J].地壳变形与地震,1999,19(4)∶15-20

[2] 杨元喜.动态系统的抗差Kalman滤波[J].解放军测绘学院学报,1997,14(2)∶79-85

[3] 柴洪洲,崔岳.动态系统的抗差Kalman滤波及其影响函数[J].中国惯性技术学报,2002(3)∶26-29

[4] 宋迎春.动态定位中的Kalman滤波研究[D].长沙∶中南大学,2006

[5] 杨元喜,高为广.两种渐消滤波与自适应抗差滤波的综合比较分析[J].武汉大学学报(信息科学版),2006,31(11)∶980-981 [6] YANG Y, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J].Journal of Geodesy,2001,75(2/3)∶109-116

[7] 杨元喜,何海波,徐天河.论动态自适应滤波[J].测绘学报,2001,30(4)∶293-298

[8] 杨元喜.动态Kalman滤波模型误差的影响[J].测绘科学,2006,31(1)∶17-19

[9] 许阿裴,归庆明,韩松辉.Kalman滤波模型误差的影响分析[J].大地测量与地球动力学,2008,28(1)∶101-104

[10] 聂建亮,吴福梅.Kalman滤波几种异常检验法[J].地球科学与环境学报,2008,30(2)∶204-208

[11] 王利,李亚红,刘万林.卡尔曼滤波在大坝动态变形监测数据处理中的应用[J].西安科技大学学报,2006,26(3)∶353-357

P258

B

1672-4623（2016）05-0103-03

10.3969/j.issn.1672-4623.2016.05.032

熊文全，高级工程师，主要从事控制测量、矿山测量、工程测量、变形监测及其应用开发工作。

2015-07-09。