利用偏置矩阵提高天绘一号卫星影像定位精度

曹彬才，邱振戈，朱述龙，曹 芳

（1.上海海洋大学 海洋测绘应用研究中心，上海 201306；2.信息工程大学 导航与空天工程目标学院，河南郑州 450000；3.宜宾职业技术学院 电子信息与控制工程系，四川 宜宾 644000）

利用偏置矩阵提高天绘一号卫星影像定位精度

曹彬才1,2，邱振戈1，朱述龙2，曹 芳3

（1.上海海洋大学 海洋测绘应用研究中心，上海 201306；2.信息工程大学 导航与空天工程目标学院，河南郑州 450000；3.宜宾职业技术学院 电子信息与控制工程系，四川 宜宾 644000）

受卫星姿态、位置精度以及传感器安装误差的影响，卫星对地定位会不可避免地产生系统误差。将定位系统误差归结为偏置矩阵，并推导了基于共线方程的表达形式。针对天绘一号高分辨影像进行实验，结果表明，该系列影像利用辅助姿态轨道数据直接定位时，存在不容忽视的系统误差；采用少量地面控制点可以解算偏置矩阵，从而将定位精度提升一个数量级，同时偏置矩阵对一定时间内的其他影像也有纠正作用。

高分辨率卫星影像；成像模型；系统误差；偏置矩阵；几何定位精度

遥感影像的高精度几何定位是影像几何处理的基础、信息量化的依据和数据复合分析的关键[1]。由于卫星定轨、测姿误差以及成像载荷的安装误差等因素，卫星影像对地定位中会不可避免地产生系统误差。与国外高分辨率卫星相比，国产测绘卫星的姿态测量精度还有数量级的差别[2]，国内学者为此提出了偏置矩阵、姿态角常差等补偿方法，并在CBERS、SOPT5和资源三号等卫星上成功应用[3-4]。天绘一号系列卫星目前有01、02星两颗卫星同时在轨运行[5]，两颗星的有效载荷、技术参数一致。目前，针对天绘一号三线阵LMCCD立体测绘相机的研究较多，2 m高分辨影像主要通过与5 m三线阵影像匹配获得地理位置信息，文献[6]通过对高分辨相机直接构建严格几何模型，实现了不依赖于三线阵相机的定位。由于各误差项之间的相关性，单独建模、逐项分析往往效果并不理想。本文将系统误差归结为综合的偏置矩阵，首先推导了基于共线方程的偏置矩阵求解方法，随后针对天绘一号高分辨影像进行了实验。

1 空间坐标系定义

建立遥感影像的严格成像模型，需要实现不同坐标系之间的转换。与严格成像模型相关的坐标系包括[6]影像坐标系、传感器坐标系、本体坐标系、轨道坐标系、星敏感器坐标系、空间固定惯性参考系（CIS）和地球固定参考系（CTS）等。

建立传感器的严格成像模型，要分别得到上述坐标系间的转换矩阵，或得到总的转换矩阵，从而实现“像点坐标”与“对应地面点坐标”间的相互转化，如图1所示。

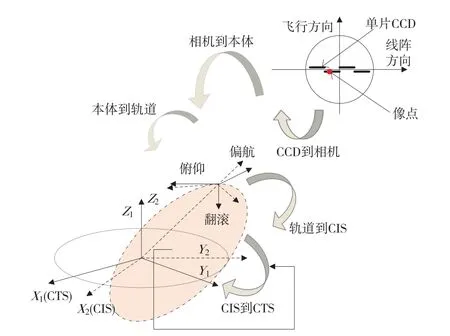
图1 严格模型的坐标转换关系

2 严格成像模型的构建

在不考虑地球曲率、大气折光等影响因素的情况下，常见的高分辨率遥感卫星严格成像几何模型如下：

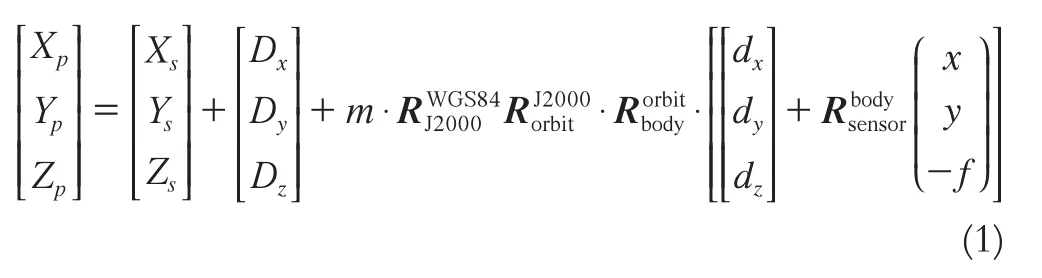
由于线元素误差会在目标定位中产生等量的平移误差，且线元素的测量精度较高，所以实际中不考虑式（1）中的线偏移量，同时传感器的像空间坐标系与卫星本体坐标系之间的旋转角度与卫星的外方位角元素相关[7]，因此简化构像模型为：

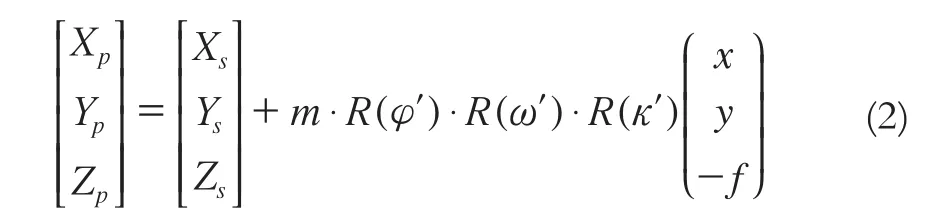
式中，φ′、ω′、κ′为简化模型的外方位角元素。

严格模型构建之后，利用视线向量定位原理，在DEM支撑下迭代求解地面坐标[8]。

3 偏置矩阵的求解

由于成像过程中存在着复杂的安装误差、星历误差或者模型处理误差，因此直接对地定位时不可避免会产生系统误差。由于对此类误差的认识不足，和这些误差的影响效果基本一致（导致各类参数之间存在着极大的相关性），想要彻底分离各种误差十分困难。因此本文也采用偏置矩阵的思想，即将所有的影响归结为一个综合的矩阵进行标定求解，将该偏置矩阵的姿态角元素视为常差。

偏置矩阵的姿态角探测模型为：

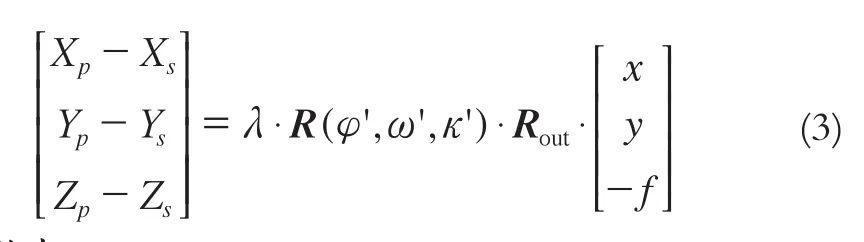
变形为：

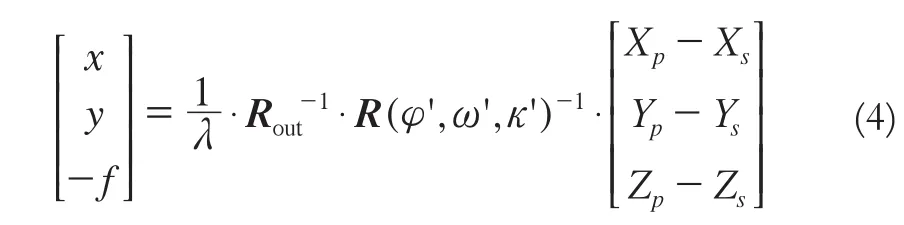
令

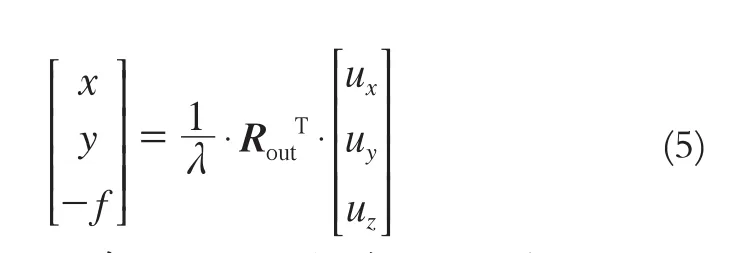
其中，偏置矩阵Rout采用YXZ转轴系统时，令

式（3）～（5）中，φ′、ω′、κ′是简化模型中的原始姿态；φ、ω、κ为偏置矩阵姿态角。

误差方程为：

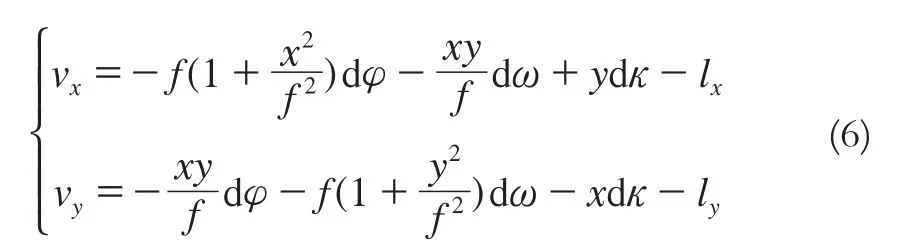
式中，lx、ly为常数项，是由像点坐标的已知值和偏置矩阵姿态角代入式（5）解得的近似值之差。当有两 个以上控制点时，构建误差方程并迭代解算偏置矩阵，当偏置矩阵角元素小于阈值时停止迭代，φ、ω、κ初始值都为0。理论上卫星运行较为平稳，因此求得的偏置矩阵不仅仅可以纠正本景影像，对一定时间跨度内的其他影像也具有一定的改正作用。

4 实验验证

选用4组天绘一号高分辨影像作为实验对象。影像1、3成像时间为2012-12-20，影像2、4成像时间为2012-11-28。其中，影像1和2，影像3和4的覆盖范围几乎一致；影像1和3，影像2和4是同一根轨道上的相邻影像，时间跨度小。4组影像覆盖嵩山检校场，该区域内平原、山地等地物要素齐全。地面控制点GCP全部采用野外GPS控制测量得到，平面精度优于0.1 m，高程精度优于0.2 m。影像1、2有30个GCP，影像3、4有10个GCP。像点坐标由多名作业员人工量测检查，精度约0.5～1个像元，实验影像和控制点的分布如图2所示。

首先利用附属文件中的姿轨参数进行直接定位实验。采用视线向量法求解控制点地面坐标，计算中，高程直接使用控制点的测量大地高，实验影像直接对地定位精度如表1所示，影像1、2的直接定位的残差分布如图3a、c所示。由表1可知，4组实验影像都具有较为优秀的直接对地定位能力，平面精度优于40 m。从图3a、c不难发现，直接定位残差具有明显的系统性。

图2 实验影像及控制点、检查点分布

随后，使用均匀分布的4个控制点对影像1、2求解偏置矩阵。影像1、2姿态角补偿后的定位残差分布如图3b、d所示，此时残差分布的方向具有随机性，并且大小与补偿前减小了一个数量级。

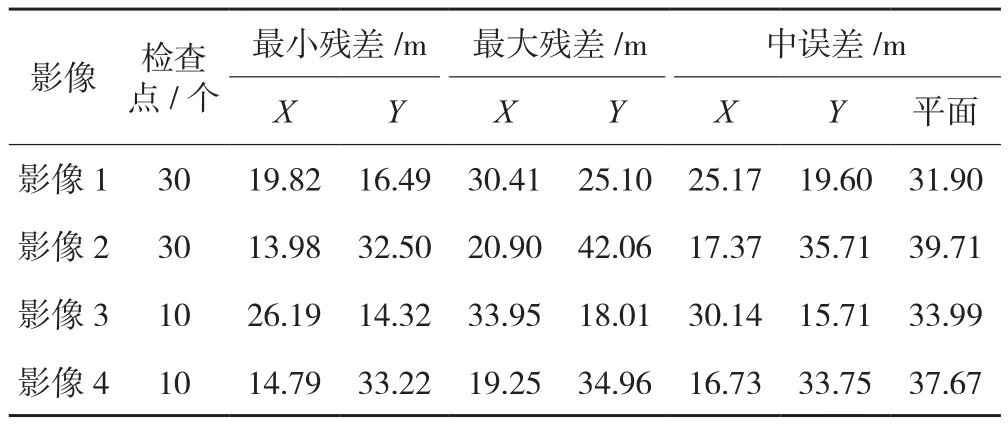
表1 天绘一号高分辨影像对地直接定位精度

图3 实验影像直接定位及姿态角补偿后的残差分布图

为了进一步说明偏置矩阵补偿的重要性和有效性，对偏置矩阵的使用范围进行了相关实验。如表2所示，影像1、2采用了4个均匀分布的GCP探测偏置矩阵，用26个检查点进行精度检查，补偿后像点的平面精度达到了3.08 m、3.28 m左右（GSD等于2.00 m，换算到像面即为1.5像素）；影像3、4用全部的点作控制，平面精度优于3.00 m。上述4组数据表明了检校的姿态角对影像本身具有很好的改正能力。表2中的1→2表示利用影像1的姿态检校值去纠正影像2，可以发现用影像1、2的检校值去相互纠正时，平面精度为18.15 m、17.07 m，虽然效果远不如影像自纠正，但又优于本身直接定位（表1中影像1、2直接定位平面精度约为31.90 m、39.71 m）；如果用检校值去纠正时间跨度较小的相邻影像，如1→3、2→4，则可以取得不错的定位精度，如影像3、4的平面精度分别达到了6.68 m、2.56 m，这表明了偏置矩阵在一定时间跨度范围内变化不大，同一组探测值对相邻影像具备一定的纠正能力，这对于无控地区的精度提升极为有利。

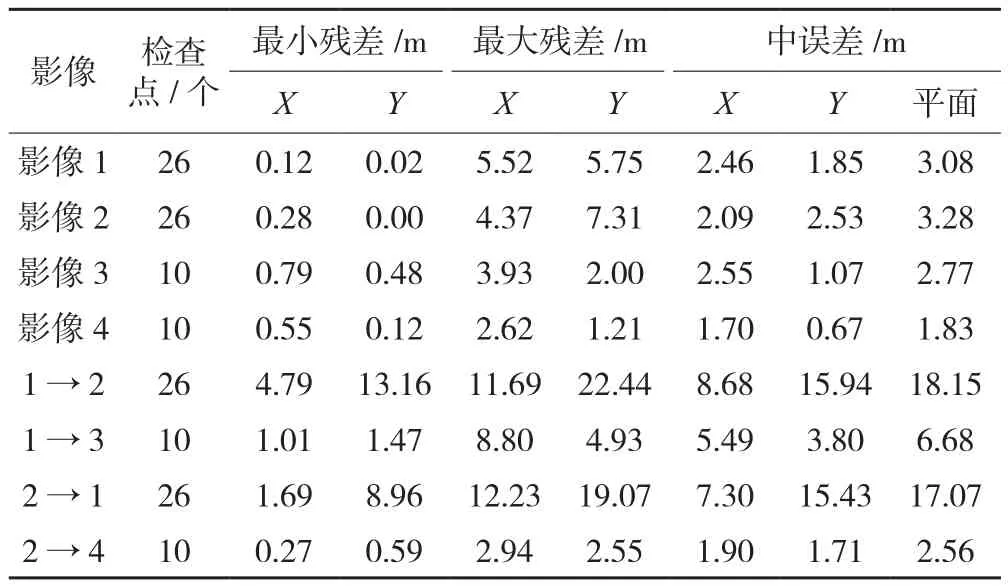
表2 姿态角常差补偿后天绘一号高分辨影像对地定位精度

此外，利用共线方程探测偏置矩阵具有很强的实用性，少量的控制点就能达到理想的纠正效果。如表3所示，采用2个控制点时便能得到很高的定位精度，且精度不随控制点的增加而提高，这对于控制数据难以获取的地区尤其重要。

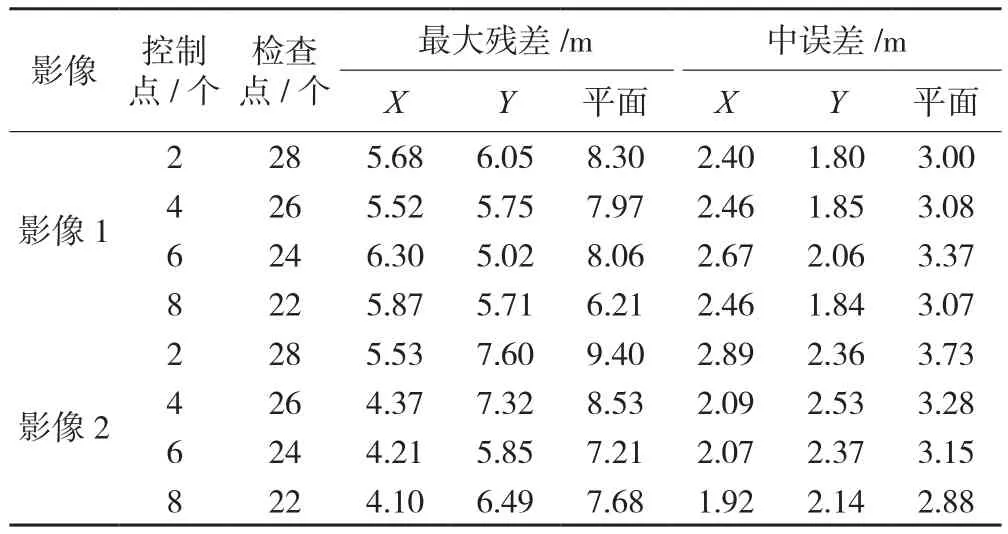
表3 不同控制点数目下姿态角常差补偿后的对地定位精度

5 结 语

本文针对天绘一号高分辨率影像，探讨了利用少量地面控制点解算偏置矩阵，从而提高影像对地定位精度的理论与方法，可得出如下结论：①天绘一号高分辨率影像对地定位中，直接使用附属的姿态轨道数据会产生系统定位误差；②本文采用的基于共线方程的偏置矩阵求解方案正确可行，在少量地面控制点参与下就能完成偏置矩阵的解算；③偏置矩阵对于本景影像的纠正效果最好，同时对一定时间跨度范围内的影像也具有一定的纠正能力。

由于实验数据的限制，本文的方法和结论还需要采用更多区域的影像数据进行更为全面的研究。

[1] 张艳,王涛,冯伍法,等.“天绘一号”卫星三线阵CCD影像自检校区域网平差[J].遥感学报,2015,19(2)∶219-227

[2] 袁修孝,曹金山.高分辨率卫星遥感精确对地目标定位理论与方法[M].北京∶科学出版社,2012

[3] 袁修孝,余翔.高分辨率卫星遥感影像姿态角系统误差检校[J].测绘学报,2012,41(3)∶385-392

[4] 徐建艳,侯明辉,于晋,等.利用偏移矩阵提高CBERS图像预处理几何定位精度的方法研究[J].航天返回与遥感,2004,25(4)∶25-29

[5] 王任享,胡莘,王新义,等.“天绘一号”卫星工程建设与应用[J].遥感学报,2012,16(增刊)∶2-5

[6] 曹彬才.多片TDI-CCD卫星影像拼接方法研究[D].郑州∶信息工程大学,2014

[7] 张永军,郑茂腾,王新义,等.“天绘一号”卫星三线阵影像条带式区域网平差[J].遥感学报,2012,16(增刊)∶84-89

[8] SPOT 123-4-5 Geometry Handbook[DB/OL].http∶// www-igm.univ-mlv.fr/～riazano/publications/GAEL-P135-DOC-001-01-04.pdf, 2004-08-20/2015-04-17

10.3969/j.issn.1672-4623.2016.05.002

P228.1

B

1672-4623（2016）05-0005-03

曹彬才，博士，主要研究方向为高分辨率卫星影像几何处理。

2015-06-25。

项目来源：国家自然科学基金资助项目（41101396）；上海市科学技术委员会科研计划资助项目（14590502200）。