基于模拟退火的量化空间关联规则挖掘

杜泽欣，李宏伟，连世伟，周 海，范瑞杰

（1.信息工程大学 地理空间信息学院，河南 郑州 450000；2. 61206部队，北京 100042）

基于模拟退火的量化空间关联规则挖掘

杜泽欣1，李宏伟1，连世伟1，周 海1，范瑞杰2

（1.信息工程大学 地理空间信息学院，河南 郑州 450000；2. 61206部队，北京 100042）

目前在空间关联规则挖掘研究中，对数据的处理和算法的改进主要针对布尔关联规则挖掘，存在对空间关联规则的量化表示不够重视等问题。在FP-growth算法的基础上增加规则的事务信息，并使用模拟退火算法，对得到的规则进行进一步挖掘，得到量化空间关联规则。

空间关联规则；量化关联规则；FP-growth；模拟退火

关联规则挖掘最先由Agrawal[1]等提出，并应用于商业活动[2]，旨在挖掘形如A→B（support，confidence）形式的规则。然而当面对结构复杂同时隐含着丰富而又不明确空间关系的空间数据[3]时，这些方法无法有效地从中得到空间数据的关联规则。针对此问题，Koperski[4]和Han首次将关联规则扩展并引入空间数据挖掘领域，提出了一种空间关联规则挖掘方法，后来逐步形成了空间关联规则挖掘[5-6]。目前大多数的空间关联规则挖掘方法只能得到形如A→B定性的关系，无法得到其定量关系。然而在实际生产生活中定量的关联规则对决策更有帮助，如利用城市内地址点定量关联规则指导城市规划和地址选址。

1 基于FP-growth的包含事务信息关联规则挖掘

FP-growth即频繁模式增长，是由Han[7]等在2000年提出的。该算法为提高挖掘效率、解决关联规则提取时需要重复扫描数据库而产生大量候选项集的问题而提出的。它采取如下策略：首先，将代表频繁项集的事务数据库压缩到一棵FP-tree，该树仍保留频繁项集的关联规则；然后，将压缩后的FP-tree划分成一组条件数据库，其中每一个数据库关联一个频繁项或“模式段”，对每个数据库进行挖掘。因此，对于每个频繁项，只需考察与其相关联的数据库，随着被考察的模式的“增长”，这种方法可以显著压缩被搜索的数据集大小。

由于构建FP-tree时，只针对事务数据库中项的类型计数，并不记录每个节点对的事务数据，因此最后得到的关联规则也没有对应的事务信息，无法进行量化规则挖掘。本文针对该问题，对现有FP-tree进行了部分改进，为树中每个节点增加了其对应的事务信息。对表1中的事务数据构建包含事务信息的FP-tree结构，如图1所示。图中每个节点信息中{}内为事务信息，具体对应如表2所示。

表1 事务数据

图1 包含事务信息的FP-tree

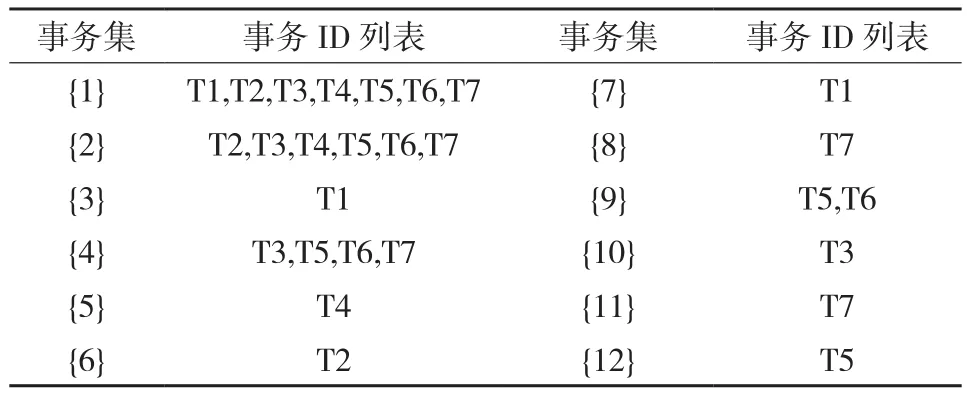
表2 FP-tree事务集对照表

对数据构建包含事务信息的FP-tree后，便可使用FP-growth提取包含事务信息的频繁模式，例如由图1中FP-tree可以得到后缀C7的频繁模式，其中，“C2,C1,C6,C7”为频繁模式；“3”为支持度计数；“”为频繁模式对应的事务数据。对于事务T1{C2,C4,C6}，其构成的FP-tree分支为C2-C6-C4，该分支内每个节点对应的事务数据均为T1，因此最后组成的FP-tree中C2-C6-C4分支内每个节点都包含事务数据T1。

2 基于模拟退火的量化关联规则提取

本文提取量化关联规则的基本思路为：假设进行关联规则挖掘的数据总个数为N，挖掘时设定的最小支持度和最小置信度分别为min_support和min_ confidence，则一条关联规则最少需要n条数据支持（n=min_support×N）。对于一条已得到的关联规则AR，共有m条事务符合该条关联规则，要提取该关联规则AR的量化表示，即从支持AR的m条数据中选出n条数据，同时使这n条数据的属性区间尽可能小，使用最终得到的n条数据的数据区间作为关联规则AR的量化表示。由于该量化关联规则使用n条数据的数据区间，所以至少有n条数据满足该量化关联规则，也就满足了关联规则的最小支持度限制；同时这n条数据本身就满足关联规则AR，也就保证了其满足最小置信度阈值。因此，量化关联规则的提取也就转换成了从m条数据中挑选n条数据，并使n条数据的数据区间尽量小的问题。假设m=100，n=50，如果要遍历所有选择可能，则需要计算种组合，这已经是一个天文数字，当数据量增加时，组合的情况会更多，因此要使用组合优化算法进行量化信息的提取。本文选用模拟退火算法进行组合优化选择。

模拟退火[8]算法的基本思想是模拟热力学中的退火过程，整个过程符合Metropolis准则[9]。该准则可以使算法在进行组合选择时跳出局部最优解，得到全局最优解。在使用模拟退火过程中，需要设定退火过程中的状态能量函数f（T）来判断每种组合的优劣。假设需要量化的关联规则前件和后件共有m项，模拟退火选取的n个事务分别为T1，T2，…，Tn，对于事务Ti，i∈（1，n），其m个项的值分别为，，…，在量化关联规则提取中，得到的量化区间越小，规则的可用性就越强，因此，参照多维空间距离公式设计了n条事务组合的状态能量函数f（T）为：

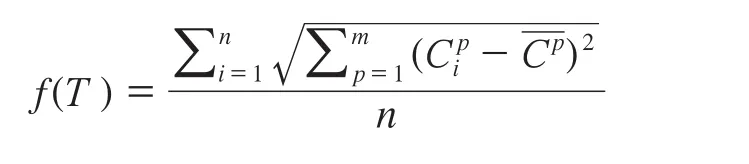
其中，

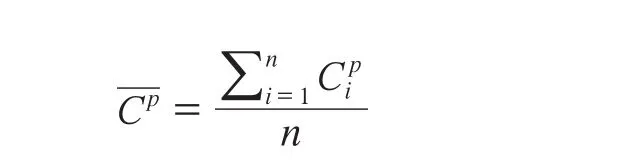
若m个项表示有m维，n个事务数据表示n个m维空间的点，则该公式可看作是n个m维空间的点到这n个点的中心的距离的平均值。f（T）越小，说明n个点分布越集中，n条事务数据的数值区间也就越小。最后通过模拟退火对包含事务信息的关联规则进行进一步挖掘，可以得到形如的关联规则，关联规则中每项后边都包含该项的量化区间信息。

3 实验分析

3.1 数据准备

本文使用某市市区内各类地址数据进行量化空间关联规则挖掘，共计8类地址数据，34 405个数据点，各类数据的代号和数量如表3所示。

表3 实验数据类别和数量情况

为了进行量化关联规则挖掘，将所有的数据点按该市的社区一级行政区划分成230个区域，每个区域看作一个事务，并构建对应的事务数据库。行政区划示意图见图2。

图2 社区行政区划示意图

3.2 提取包含事务的量化关联规则

在进行关联规则挖掘时，当支持度相同、置信度较高时得到的关联规则集一定是置信度较低时得到关联规则集的子集；当置信度相同、支持度较高时得到的关联规则集一定是支持度较低时得到关联规则集的子集；当支持度不变时，得到的关联规则数量随置信度的增加而减少；当置信度不变时，得到的关联规则数量随置信度的增加而减少。

于是，在进行关联规则挖掘时，为了研究支持度和置信度对关联规则产生结果的影响，只需抽取几个置信度和支持度的值进行实验即可获得在此区间内产生关联规则的整体趋势。本文实验分别采用的支持度为30%、40%、50%、60%、70%、80%，置信度为40%、50%、60%、70%、80%、90%。以前文得到的事务数据库为数据，对支持度和置信度交叉配对依次进行关联规则挖掘，共进行36次实验，每次所得关联规则个数如表4所示。

表4 不同支持度和置信度下得到的规则数量

由表4可以看出，当置信度不变时，支持度由30%增长到50%，规则的数目变化不大，而从50%到80%的每次增长规则数目都会急剧减小；当支持度不变时，置信度增加，规则数目减少幅度较小。由此可见，该关联规则挖掘得到的所有结果置信度基本趋于稳定且置信度较高，因此，使用置信度无法有效地对规则进行筛选；同时，在支持度小于50%时，支持度变化对规则数目影响也很小，只有支持度从50%增长到60%和从60%增长到70%两次变化时，规则数目下降较快，达到了对规则很好的筛选效果。本文选取支持度为70%，置信度为80%时得到的32条规则进行进一步挖掘。对生成的32条规则进行整理，如果规则A与规则B的后件相同，且B的前件是A的前件的子集，则只保留规则A，最后得到3条典型的关联规则，如表5所示。由于在挖掘过程中始终保留着事务信息，因此得到的量化规则也保留了其对应事务数据集。

表5 关联规则

3.3 提取量化规则

得到关联规则后，根据其对应的事务数据集可直接找到其对应的关系数据。表6中所示为规则{医院，餐饮，娱乐}→商店对应的5条事务数据。

表6 事务数据

由于按行政区划划分后得到的规模大小不一，因此每个区域内包含的数据总量也不一样。当区域的规模相差较大时，2个区域内包含的数据总量也相差较大，转换得到的关系数据库中，同一类型项目的绝对数量也就可能相差较大，如表6中第1条数据与第2条数据相差10倍之多。当项目数量相差较大时，无法根据关系数据库得到各项目间的准确绝对数量关系。因此需要对数据进行变化，对每一条事务数据进行数据归一，注重每条事务中各项的比例关系，忽略事务中所有项的数据总量，将所有的事务数据的数据总量统一，使所有事务数据具有相同的权重。因此，对规则对应的事务数据进行归一化，表6中的数据归一化后如表7所示。

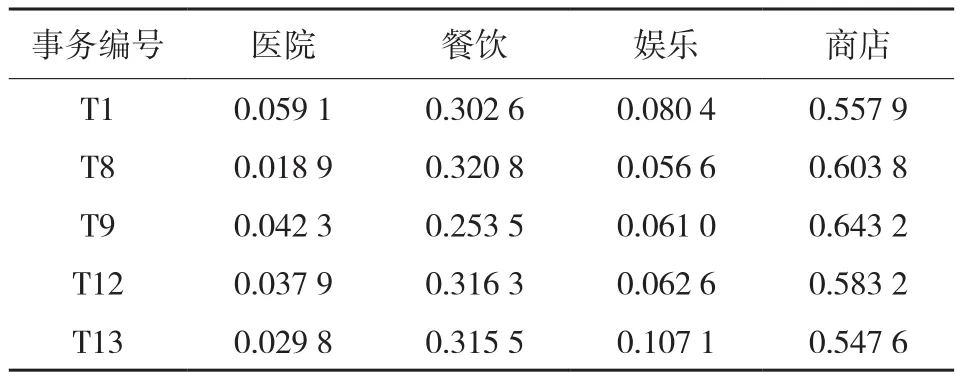
表7 归一化后的事务数据

表8 量化关联规则

量化关联规则中，每项后小括号内2个数值表示该项在量化关联规则所有项中所占比例的上下阈值。例如，表8中第1条量化关联规则{学校（0.01,0.12），医院（0.02,0.12）}→商店（0.78,0.97），某区域内学校、医院和商店三者中，学校所占比例在0.01～0.12，且医院所占比例在0.02～0.12时，商店所占比例应该在0.78～0.97。根据得到的量化关联规则，可以找到该市商店数量过剩的区域，如图3中红色区域所示。根据此结果，在为新商店选址时可以避开这些区域，为选址提供参考信息。

P208

B

1672-4623（2016）05-0008-03

10.3969/j.issn.1672-4623.2016.05.003

2015-04-10。

项目来源：国家自然科学基金资助项目（41271392）；国家自然科学基金青年基金资助项目（41401463）；河南省科技攻关计划（高新技术领域）资助项目。