站姿人体与轻质结构水平耦合振动单自由度等效模型参数研究

杨 予，薛圣雅，蔡其茅

（浙江理工大学 建工学院土木系，杭州 310018）

站姿人体与轻质结构水平耦合振动单自由度等效模型参数研究

杨 予，薛圣雅，蔡其茅

（浙江理工大学 建工学院土木系，杭州 310018）

给出了一种通过实验获得人与轻质结构水平耦合振动单自由度等效模型参数的方法。首先采用单自由度振动台对人与结构水平方向耦合自由振动位移时程进行测试，然后在推导出振动台水平振动阻尼比计算公式的基础上通过最小二乘法拟合得出人体等效自振频率和等效阻尼比。测试中考虑了人体正面与振动方向夹角分别为0度、45度和90度三种状态以及有无抓握扶手对测试结果的影响。分析结果表明，在结构/人体质量比约为0.25时人体等效自振频率在0.1 Hz～0.48Hz，等效阻尼比在0.05～0.39之间变化，当人双手抓握扶手时等效自振频率和等效阻尼比最大。

振动与波；水平耦合振动；单自由度模型；参数识别；等效阻尼比

随着材料和技术的发展，建筑结构有轻量化发展趋势。工程经验显示，当建筑物质量较轻，接近其承托人群的质量，甚至比后者还要轻时，人与结构耦合振动效应不容忽视[1]。在进行振动评价时，其中一个关键问题是对人体结构进行合理的简化并给出适当的模型参数[2]。

从目前研究成果来看，常用的人体简化模型可分为三类：第一类为多自由度模型，如Subashi[3]等和吴静波等[4]采用的多个质点与多个弹簧-阻尼器相连接的复杂多自由度人体站姿模型，这类模型理论上具有较高的精度，能够模拟人体各部分的复杂运动，还可以根据各个部分的动力响应分析结果来进行人体舒适性设计，然而由于涉及人体多个部分的质量、刚度、阻尼参数的确定，这些模型实际应用时相对困难，且在进行人与结构耦合振动计算时自由度数量庞大，建模复杂程度也最高；第二类为单自由度简化模型，例如：Matsumoto、Wei和Griffin[5-6]比较分析了将竖向振动站姿人体简化为单自由度和2自由度简化模型对应的拟合误差，结果表明单自由度模型与2自由度模型相比仅在相位计算和5 Hz主共振频率上精度稍差；第三类为等效附加质量模型，例如付明科等[7]将站姿人体简化为前后向的等效附加质量模型来模拟人对结构水平振动频率的影响，并通过试验验证了此模型的有效性。

根据上述分类可知，由于单自由度模型具有能够反映人体的频率和阻尼特性，且在分析计算上相对便利的特点，在各类研究中广泛被采用，例如：Dougill8]，G.Busca[9]，秦敬伟[10]等人分别在各自的研究中采用了人体单自由度模型。然而，从各个文献所采用的具体参数来看，目前人体水平单自由度简化模型在实验研究方面的积累还相对不足，例如：在曹文斌等[11]进行的研究中，认为人体水平前后向频率范围为0.236 Hz～3.748 Hz，人体水平左右向频率范围为0.194 Hz～5.32 Hz；在Matsumoto等[12]进行的研究中，得到人体水平前后向频率为0.125 Hz左右，人体水平左右向频率为0.5 Hz左右，而文献[11]和[12]中均未给出工程分析所需的人体模型阻尼比取值范围。由此可见，人与结构水平耦合振动时(例如建筑结构在承受人群荷载时同时受到水平风振或地震作用)单自由度模型参数的取值问题尚需深入研究。

综上所述，本研究的目的是通过实验和数值分析推导人体站姿水平振动单自由度模型参数，主要方法和手段是通过振动实验台观察记录人与结构耦合自由振动时程，并采用合理的拟合方法得出具有最佳近似度的等效自振频率和等效阻尼比。

1 耦合振动模型

本研究采用的人体站姿水平振动单自由度模型如图1所示，即把人体简化为水平连接在结构上的单自由度体系。在与下方结构一起构成2DOF体系后，其自由振动方程组如式(1)所示。

图1 人体站姿水平振动单自由度模型示意图

当初始条件为已知时，可采用数值积分方法(如Wilson-θ法等)对式(1)进行求解，从而得到该体系在任意时刻的瞬时自由振动位移、速度和加速度值。

根据文献[13]中的论述可知，由于人体对振动的响应十分复杂，按一维简化模型分析所得结果一般情况下很难与实际振动完全一致，为使其具有工程应用价值，应使按简化模型求出的振动反应为实际振动反应的某一最佳数值逼近。为便于工程应用，本研究中Mh和Ms分别取人体和结构的实际质量，而将人体等效刚度Kh、阻尼Ch视为待定参数。通过将数值计算求出的下部结构位移时程Us(Ch、Kh、t)与实测得到的位移时程us(t)做最小二乘法拟合，使得式(2)所示的误差函数F取极小值，即可求得出具有最佳近似度的Kh、Ch或人体等效频率fh和等效阻尼比ξh，具体步骤可参考文献[13]。

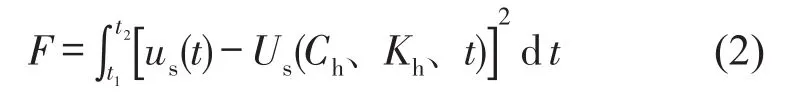
2 实验概况

2.1 试验台设计

实验中采用单向水平振动的平板小车作为振动台，其设计简图如图2所示，通过更换小车端部的弹簧或在小车上固定砝码可以在一定范围内调整其水平振动参数。由图2可知，小车受到的水平滚动摩擦阻力并非常数而与其受到的压力等因素有关。

图2 单自由度振动台示意图

为便于考察人体对振动台侧向振动的影响，研究中取相对较轻的结构重量(结构/人体质量比在0.25附近)和较低的结构自振频率(4.61 Hz附近)，其具体参数见表1。

表1 人与结构耦合振动实验参数条件

测试期间采用联能YE7600型动态采集系统和YBD-200型位移传感器以及便携PC机等设备对小车的水平位移时程进行记录，采样频率设置为2kHz。

2.2 试验参数

考虑到建筑物中人的站立朝向有多种可能性，为分析其对振动参数的影响，令志愿者站立朝向分别与小车振动方向成0°、45°和90°，尽量保持双手下垂的上体自然状态，对小车赋予一固定大小的初始位移(A=10 cm)后突然释放做自由振动并进行多次测试，如图3(a)-图3(c)所示，考虑到生活中常见的人体站立扶栏杆状态，还对测试者面向振动方向手抓握扶手并保持上体自然状态下的小车水平位移时程进行了测试，如图3(d)所示。

图3 人体在小车上的站立朝向与姿态示意图

3 结果初步分析

作为初步对比，图4中给出了小车自由振动、人面朝小车振动方向站立扶手/未扶手三种状态下测得的规格化自由振动位移时程曲线。

图4 小车三种工况下振动时程对比

由图4可见，与空载时的自由振动位移时程相比，小车载人后其振幅衰减很快，而当人双手抓握扶手时，振幅衰减速率又比未握扶手时有明显增加。从同一时间段内往复振动次数(频率)上看，人静止站立与小车耦合振动时测得小车振动次数相比小车空载略有增加。

上述振动时程测量结果还表明小车载人后整个系统的阻尼有所增加，其原因有：

(1)小车受压时(不计人体质量惯性力影响)，轮子的水平滚动摩擦阻力增大导致小车自由振动阻尼比增加；

(2)人体与小车耦合振动产生的系统阻尼效应。

对于后者，研究中根据耦合振动位移时程采用式(2)进行拟合；而对前者，由于很难在施加压力时不同时改变小车整体质量，所以采用下面的理论方法进行估计：

假定空载状态下的小车阻尼比为ξs，则黏滞阻尼系数为小车自振圆频率。根据黏滞阻尼系数的定义，设小车水平位移为x，则小车在做自由振动时，任意时间段t内阻尼力做功为

其中L为t时间内小车运动的总水平距离，μr为滚动摩擦系数，N为车轮受到的竖向压力。令阻尼力和滑动摩擦力所做耗散功相等可得W1=W2，如取t=0时刻初始位移和速度分别为x(0)=A，(0)=0，并取t= 0～1/4周期时间段即[0，π/2ω]内的耗散功相等，易知此时有L=A，由上述关系可得

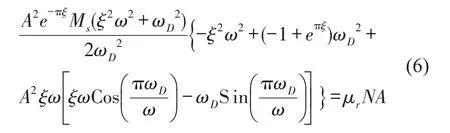
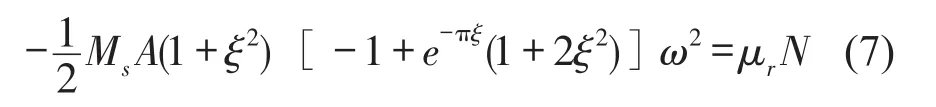
将小车空载情况下的振动参数ωξs和小车质量产生的竖向压力N1=Msg代入式(7)，并根据实验给定的初始位移A值，即可求出滚动摩擦阻力系数μr，再将μr和小车与人共同产生的竖向压力N2=(Ms+Mh)g

考虑到阻尼比很小时ω≈ωD，上式还可简化为代入式(7)，采用数值方法求解方程即可得到小车因滚动摩擦阻力增大而增加的阻尼比，最终结果列于表2。

表2 小车载人前后阻尼比分析结果

由表中数值可知，小车载人时由于受到的竖向压力增加而使其自身的阻尼比提高了约6倍。

4 振动参数拟合结果

在考虑了竖向压力使得小车水平自由振动阻尼比增大的因素后，将人-车系统在自由振动状态测得的小车位移时程按式(2)进行最小二乘法拟合，得到的典型单次自由振动拟合曲线如图4所示(志愿者一，0°方向自然站立，拟合误差均方根RMS=0.009 1)。由拟合情况可知，给出的模型参数在分析结构耦合振动幅值和频率上具有较好的工程实用价值。

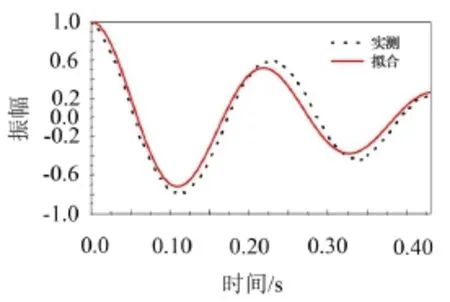
图5 实测位移时程的最小二乘法拟合情况

将人体朝向与小车运动方向成0°、45°、90°以及双手放在扶手上的参数拟合结果取多次实验的平均值绘制成直方图进行对比可得到图6。由图6可见，当志愿者站立朝向不同、抓握扶手状态不同时得到的等效频率在0.1 Hz～0.48 Hz之间变化，等效阻尼比在0.05～0.39之间变化。

图6 等效频率和阻尼比对比

由图6中的对比可知，当志愿者面向振动方向自然站立时等效频率最小，抓握扶手时等效频率最大；而对于等效阻尼比来说，志愿者面向振动方向抓握扶手时等效阻尼比最大，面向90°方向自然站立时等效阻尼比最小。对比45°和90°朝向站立的频率和阻尼比拟合结果可知，这两个姿态的振动参数变化无明显规律。

将上述结果与实验过程中观察记录到的志愿者身体摇摆状况相对照分析可知，人体具有一定的无意识平衡调节能力，不同的志愿者个体之间有明显差异，所以应通过大量实验取平均值确定振动参数。

5 结语

从2DOF体系自由振动的定义出发，给出了一种通过对实测自由振动时程曲线做拟合求出人体水平振动单自由度简化模型参数的方法，原理简单明确。在此基础上根据多次实验测试结果研究了在结构/人体质量比约为0.25、结构自振频率为4.61 Hz时人体与结构耦合振动的等效频率和等效阻尼比。虽然研究中所采用的时域拟合方法与Matsumoto[12]、陆建等[14]采用的振动台激振扫频识别原理不同，但在结果中仍可找到一些共同点：

(1)未抓握扶手时，人体各向站姿等效自振频率识别结果在0.1 Hz～0.48 Hz范围内变化，这与Matsumoto等人通过扫频得出的人体直立时水平共振频率在0.125 Hz～0.5Hz范围内变化的结论[12]接近(该文献中人体平均质量76.5 kg，但未给出人体/结构质量比)；

(2)Matsumoto等人在研究中发现的受测者个体阻尼特性相差较大的结论与本研究中得出的测试者个体等效阻尼比波动的情况相吻合，而本研究中等效阻尼比的最大值与陆建等[14]采用的值相近。

利用文中方法，还进行了一些具有特色的研究与探讨：实验中考虑了人体正面朝向与振动方向的夹角分别取0°、45°和90°以及双手有无抓握扶手的影响，根据实验结果可得如下结论：

(1)本研究给出的模型参数在分析结构耦合振动幅值和频率上具有较好的工程实用价值。

(2)结构/人体质量比约为0.25时的人体站姿等效水平自振频率在0.1 Hz～0.48 Hz范围变化，抓握扶手时自振频率最大。

(3)结构/人体质量比约为0.25时的等效阻尼比在未抓握扶手时在0.05～0.39范围变化，在双手抓握扶手时阻尼比最大。

[1]马斐，张志强，李爱群.大跨钢楼盖人群荷载激励下减振控制分析[J].振动、测试与诊断，2013，33(3)：514-520.

[2]张志飞，徐中明，贺岩松，等.人体全身振动评价研究[J].噪声与振动控制，2010，30(2)：149-155.

[3]SUBASHI G H M J,MATSUMOTO Y,GRIFFIN M J. Modelling resonances of the standing body exposed to vertical whole-body vibration:Effects of posture[J].Journal of Sound and Vibration,2008,317:400-418.

[4]吴静波，谌勇，李兆俊，等.抗冲地砖对立姿舰员的冲击防护效能分析[J].噪声与振动控制，2011，31(4)：6-10.

[5]MATSUMOTO Y,GRIFfiN M J.Mathematical models for the apparent masses of standing subjects exposed to vertical whole-body vibration[J].Journal of Sound and Vibration,2003,260:431-451.

[6]WEI L,GRIFFIN M J.Mathematical models for the apparent mass of the seated human body exposed to vertical vibration[J].Journal of Sound and Vibration.1998,212(5):855-874.

[7]付明科，叶茂，曹文斌，等.基于人-结构耦合振动试验的等效人体模型[J].结构工程师，2015，31(2)：194-201.

[8]DOUGILL J W,WRIGHT J R,PARKHOUSE J G,et al. Human structure interaction during rhythmic bobbing[J].Structural Engineer,2006,84(22):32-39.

[9]BUSCA G,CAPPELLINI A,MANZONI S,et al. Quantification of changes in modal parameters due to the presence of passive people on a slender structure[J].Journal of Sound and Vibration.2014,333(21):5641-5652.

[10]秦敬伟，杨庆山，杨娜.人体-结构系统静态耦合的模态参数[J].振动与冲击，2012，31(15)：150-157.

[11]曹文斌.人-结构系统水平振动试验和理论模型研究[D].广州：广州大学，2014：36-38.

[12]MATSUMOTO Y,GRIFFIN M J.The horizontal apparent mass of the standing human body[J].Journal of Sound and Vibration,2011,330(13):3284-3297.

[13]杨予，杨云芳，洪震，等.人体站姿竖向振动等效单自由度模型参数研究[J].振动与冲击，2012，31(23)：154-157.

[14]陆建，周叮，李枝军，等.直立人体-结构侧向相互作用动力学特性分析[J].南京工业大学学报（自然科学版）. 2015，37(6)：61-68.

Study on Equivalent Single-DOF Horizontal Vibration Parameters for the Standing Human Body Coupling with Light Structures

YANG Yu,XUE Sheng-ya,CAI Qi-mao
(School of Civil Engineering,Zhejiang Sci-Tech University,Hangzhou 310018,China)

A method to identify the parameters of an equivalent single-DOF horizontal vibration model for a standing human body coupling with light structures is provided.A single DOF test rig is used to test the horizontal free vibration timehistory of human body-structure interaction.The damping ratio of the rig is estimated.Least square method is applied to identify the equivalent human body free vibration frequencies and the damping ratios.The influencing factors such as human body orientations including 0,45,and 90 degrees and gesture of grasping handrail are considered.The result shows that the equivalent frequencies of the human body vary from 0.1 to 0.48 Hz and the damping ratios vary from 0.05 to 0.39 when the mass ratio of the structure to the human body is nearly 0.25.It also shows that the posture of grasping handrail yields the maximum equivalent free vibration frequency and damping ratio of the human body.

vibration and wave;horizontal coupling vibration;single-DOF model;parameter identification;equivalent damping ratio

TU311.3

：A

：10.3969/j.issn.1006-1335.2016.06.038

1006-1355(2016)06-0192-05

2016-06-17

浙江省教育厅资助项目(Y201122128)

杨予（1975-），男，南宁市人，副教授，主要研究方向为结构动力学。E-mail:yangyu@zstu.edu.cn