考虑投标者后悔的一级密封拍卖的最优投标策略
高广鑫,樊治平
东北大学 工商管理学院,沈阳 110167
考虑投标者后悔的一级密封拍卖的最优投标策略
高广鑫,樊治平
东北大学 工商管理学院,沈阳 110167
许多实验研究表明,投标者在拍卖过程中表现出的预期后悔心理行为会对投标策略产生影响,在这种情况下如何确定最优投标策略是一个值得关注的问题。
针对一级密封拍卖的最优投标策略确定问题,分别采用线性函数和非线性函数刻画投标者的获胜者后悔和失败者后悔心理行为,构建非线性拍卖模型,通过模型求解分析最优投标策略;进一步地,给出确定拍卖模型中描述投标者后悔心理行为参数的实验方法,并通过一个关于SO2排污权拍卖的实例分析说明非线性拍卖模型及实验方法的可行性和潜在应用。
研究结果表明,最优投标策略与投标者价值和后悔行为有关;最优投标策略为获胜者后悔参数的减函数,且为失败者后悔参数的增函数;完全理性的最优投标策略是所得最优投标策略的特例;当投标者人数非常多时,完全理性的最优投标策略是报出自身的真实估价;在仅考虑投标者获胜后悔情形下,其最优投标策略与线性拍卖模型所得结果相同,且低于完全理性的最优投标策略;在仅考虑投标者失败后悔情形下,其最优投标策略高于完全理性的最优投标策略;与线性拍卖模型比较,由非线性拍卖模型得到的最优投标策略更接近于真实投标报价。提出的非线性拍卖模型为解决现实拍卖中考虑投标者心理行为的最优投标策略确定问题提供借鉴。
一级密封拍卖;预期后悔心理行为;非线性拍卖模型;投标策略;实验方法
1 引言
在现实生活中,古董交易、农畜产品买卖、矿产开采权转让等经济活动大多是通过拍卖实现的[1],此外,拍卖也常被用于定向购买商品或服务[2]。通常,拍卖有多种形式,如英式拍卖、荷式拍卖、一级密封拍卖和二级密封拍卖等[3],不同拍卖形式下的投标者价值、拍卖定价及配置效率均存在差异[4]。其中,一级密封拍卖是最为常见的拍卖形式[5],是指投标者以书面密封形式出价竞标,且出价最高者以其报价获取标的物[6]。关于一级密封拍卖投标策略的行为实验研究表明[7],在拍卖过程中投标者往往表现出预期后悔心理行为,并且投标者的后悔心理行为会对投标策略产生影响。因此,本研究在考虑投标者预期后悔心理行为的情况下,通过构建并求解考虑投标者后悔心理行为的一级密封拍卖模型,对最优投标策略进行分析,并给出确定拍卖模型中描述投标者后悔心理行为的参数的实验方法。
2 相关研究评述
关于考虑投标者后悔心理行为的一级密封拍卖问题的研究成果中,与本研究最直接相关的是ENGELBRECHT-WIGGANS et al.[7-8]针对一级密封拍卖中投标者后悔心理行为对投标策略影响的研究,他们认为在现实拍卖中,出现偏离风险中性纳什均衡投标价(risk neutral Nash equilibrium, RNNE)的超投标或低投标现象是由投标者的后悔心理行为引起的。ENGELBRECHT-WIGGANS[9]认为在一级密封拍卖中,投标者获得的效用不仅依赖于其期望的货币收入,同时也依赖于获胜者后悔和失败者后悔两方面的情感因素,也就是说投标者的后悔心理行为将会对其投标策略产生影响。通常情况下,当投标者对于获胜者后悔敏感时会降低平均投标价,而当投标者对于失败者后悔更敏感时便会提高平均投标价[8]。而FILIZ-OZBAY et al.[10]侧重于研究预期失败者后悔对于投标策略的影响,认为超投标现象主要是由失败者后悔导致的,而在投标者获胜的情形下,其一般不会预期后悔,并且不会出现明显的低投标现象。
此外,还有学者进行投标者后悔对投标策略影响的实验研究。ENGELBRECHT-WIGGANS et al.[11]利用与后悔心理行为相关的反馈信息作为变化的实验条件,分析在不同实验条件下投标者后悔与其投标策略的关系;DU et al.[12]通过实验方法研究投标者在投标过程中预期后悔与实际经历的后悔之间的差异,分析预期后悔对投标策略的影响,并得到预期后悔大于实际经历的后悔的结论;ASTOR et al.[13]从心理学的视角研究获胜者和失败者后悔,并通过心理学实验操纵投标者情感进程来验证ENGELBRECHT-WIGGANS et al.[8]研究工作中不同类型的后悔参数的准确性。
综上,已有研究解释了在拍卖中出现的不等于RNNE的超投标或低投标等非理性现象,对考虑投标者行为的一级密封拍卖的投标策略研究做出了重要的贡献。需要特别指出的是,ENGELBRECHT-WIGGANS et al.[8]是在投标者对于后悔感知是风险中性的假设基础上,通过采用线性函数刻画投标者的获胜者后悔和失败者后悔心理行为,并分析其对于投标策略的影响,他们认为次高价与投标者获胜价或获胜价与投标者价值的差值的增长与投标者后悔值的增长均成等比关系。但是,已有研究表明[10],在现实拍卖中,相对于投标所获得的期望效用,投标者往往更关心自己是否获胜,因此,其通常会事先预期失败者后悔,而对于获胜者后悔一般不会有所预期,且不会出现明显的低投标现象。也就是说,投标者对于失败者后悔是敏感的,而对于获胜者后悔是相对不敏感的,这是由于获胜者后悔影响的是投标者获得的期望效用大小,而失败者后悔影响的则是投标者的最终获胜状态[8]。进一步地,投标者认为其对获胜价与投标者价值之间的差值愈大愈敏感[14],即投标者预期失败者后悔值的变化程度要大于获胜价与投标者价值的差值的变化程度,在这种情况下,采用线性后悔函数刻画投标者的失败者后悔行为是有局限性的。此外,在已有研究中,关于确定描述投标者后悔心理行为参数的具体实验方法尚不多见。因此,有必要针对ENGELBRECHT-WIGGANS et al.[8]的工作进行深入的扩展研究。
基于上述分析,本研究进一步研究针对考虑投标者后悔心理行为情况下的一级密封拍卖的投标策略确定问题,通过分别采用线性函数和非线性函数刻画投标者的获胜者后悔和失败者后悔心理行为,并通过构建拍卖模型及模型求解,对最优投标策略进行分析,同时给出确定拍卖模型中描述投标者后悔心理行为的参数的实验方法。
3 问题描述
这里考虑不可分割的单物品一级密封拍卖最优投标策略确定问题。记A为参与投标的n个投标者的集合,A={A1,A2,…,An},其中,Ai为第i个投标者,且投标者Ai与其他(n-1)个竞标者同时参与投标。令vi为投标者Ai对标的物的估价(即投标者价值),0≤vi≤1;bi为投标者Ai针对标的物的投标价,且0≤bi≤vi,若投标者Ai获胜,则其收益为(vi-bi)。令v-i为除Ai外的其他(n-1)个竞标者中的任一估价,b-i为除Ai外的其他(n-1)个竞标者中任一估价的投标价,v-i的分布函数为G(·),z为其他(n-1)个竞标者中针对标的物的最高投标价,假设z服从概率分布,其分布函数为F(·),且密度函数为f(·)。
在做出决策时,人们通常会被一种反事实想法所困扰,即如果其选择不同的决策方案,将可能会有更有利的结果,从而产生后悔的负面心理行为[15]。这里,考虑投标过程中投标者的两种预期后悔心理行为,即获胜者后悔行为[8]和失败者后悔行为[16],具体描述如下。
(1)获胜者后悔。假设拍卖结束后,投标者Ai不仅会得知获胜状态,当其投标获胜时,还可以知道次高价信息。这种情况下,若该投标者预期此次拍卖投标获胜,即P(bi>z),则意味着投标者Ai为了赢得标的物将多支付(bi-z)个单位数量的货币。实际上,其只要出比z高最小单位数量的投标价便可获胜,并且支付将会减少。通过与次高价z比较得知,Ai会为可能多支付的不必要的货币而产生后悔预期,进而在实际拍卖中,Ai便会相应地降低投标价,通过缩小与次高价之间的差距来增加自己的收益。
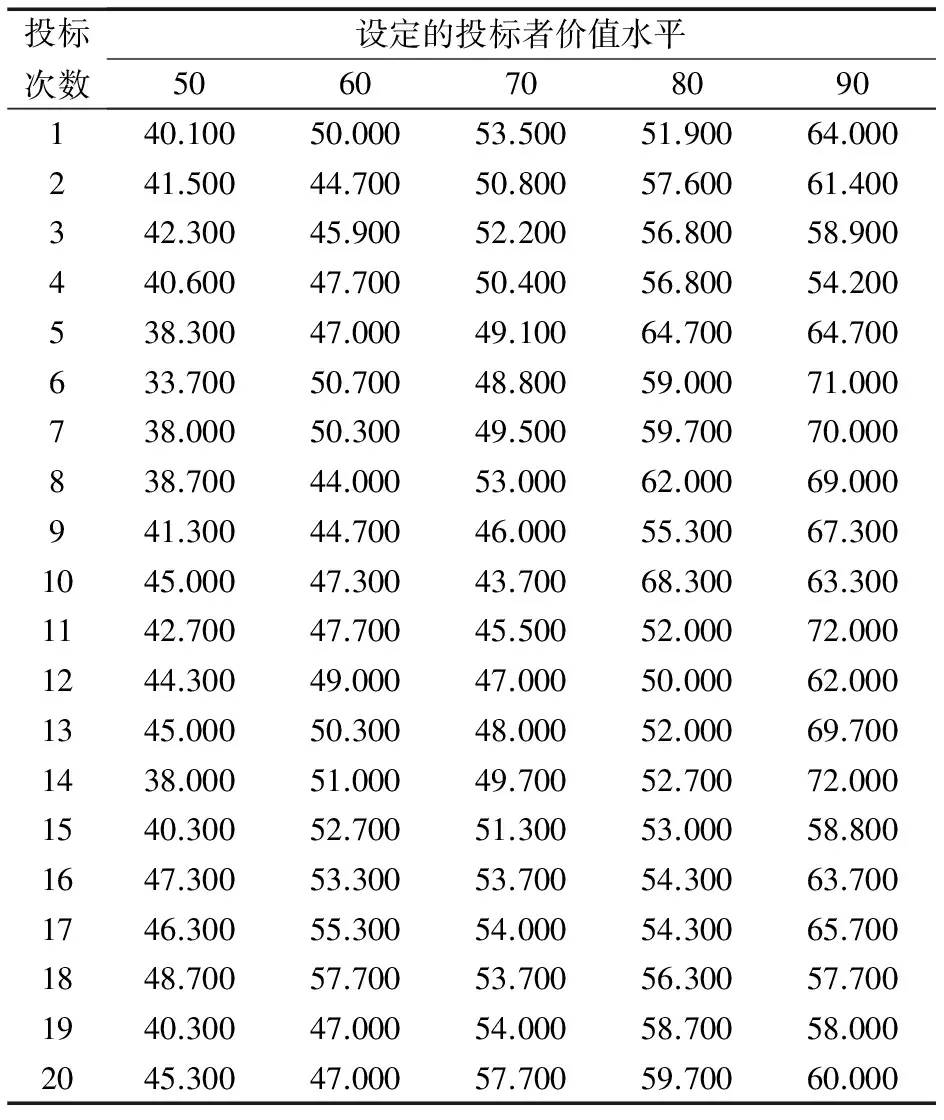
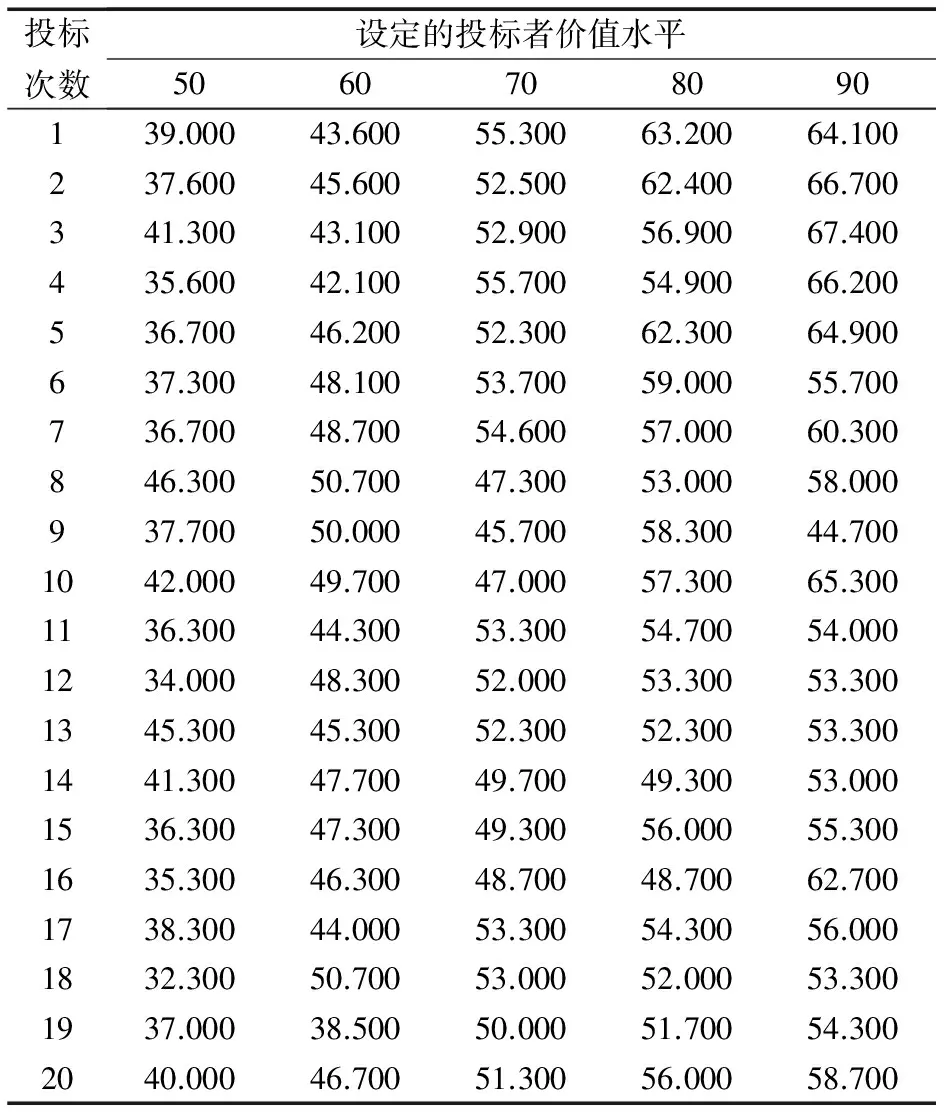
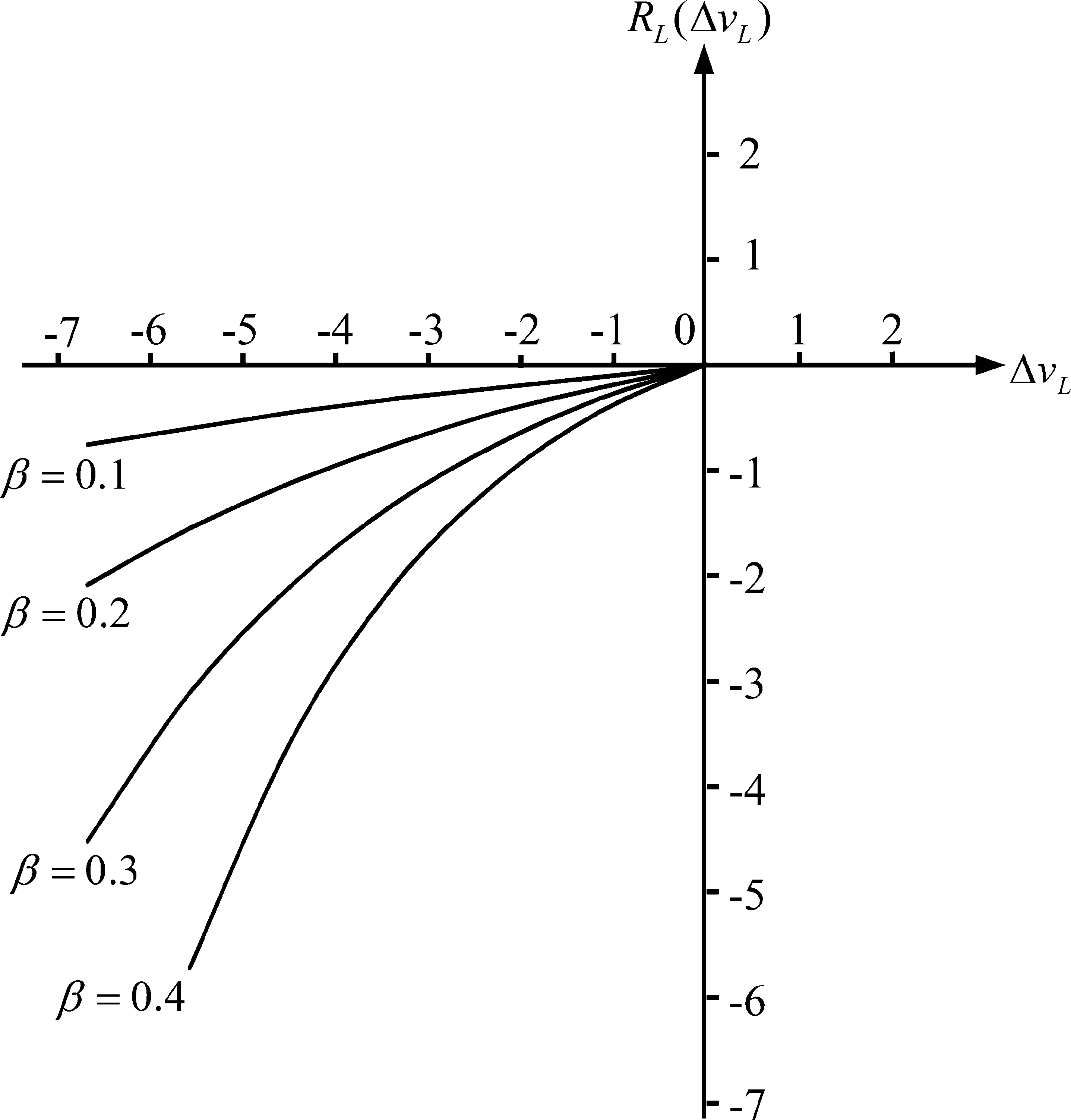
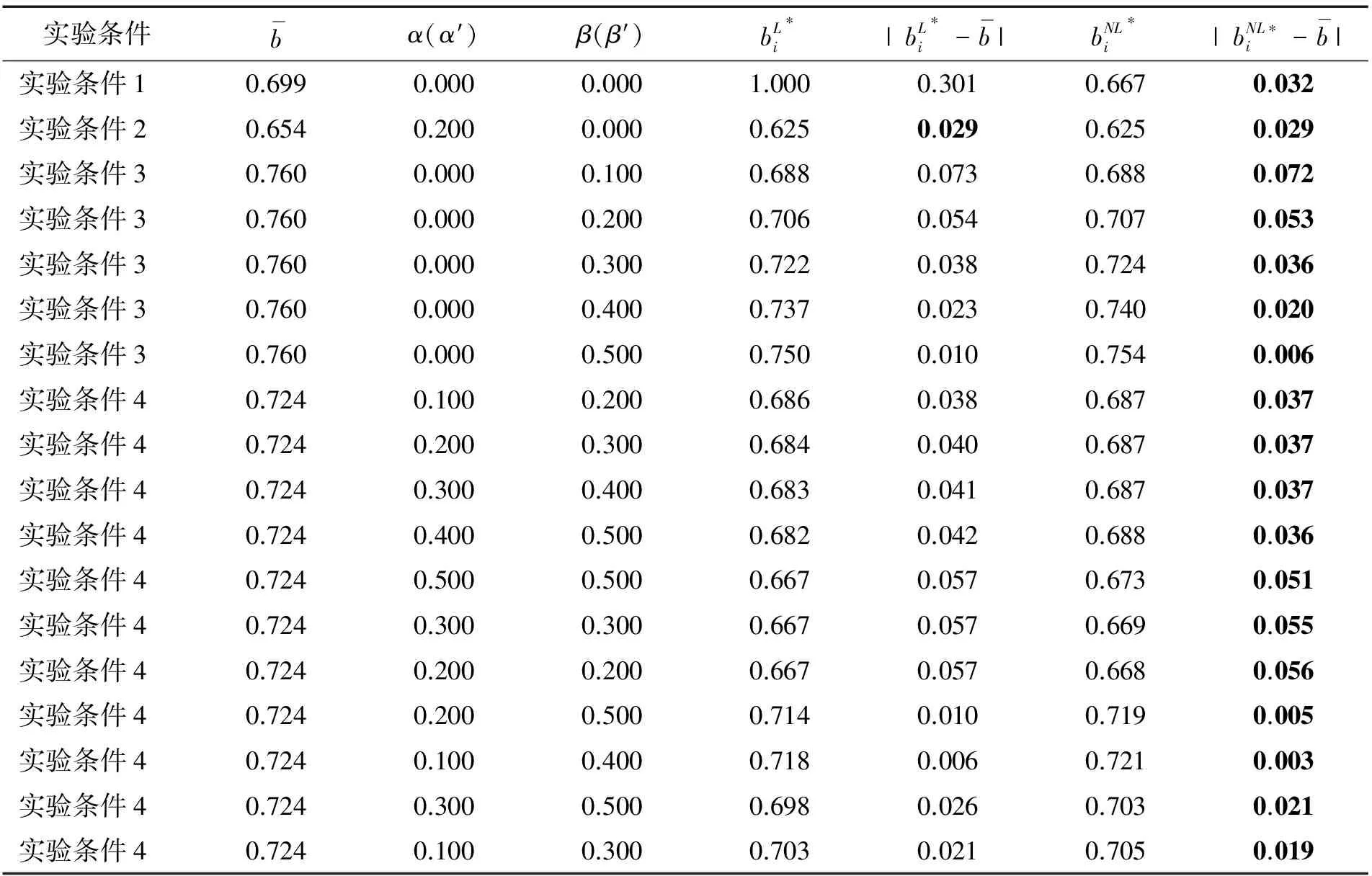
(2)失败者后悔。假设拍卖结束后,投标者Ai不仅会得知获胜状态,当其投标失败时,还可以知道获胜价信息。这种情况下,若该投标者预期此次拍卖投标失败,且获胜价是在其可承受的范围内,即P(bi 显然,影响投标者事前期望效用的因素体现在两个方面,一个是投标者获胜的期望收益;另一个是投标者的预期后悔感知,这里可能是获胜者后悔或者是失败者后悔。本研究要解决的问题是,在考虑影响投标者事前期望效用的因素的情况下,如何构建考虑投标者后悔行为的一级密封拍卖模型,并通过模型求解确定最优投标策略。相应地,还要考虑如何确定模型中的相关参数值。 为了解决上述提及的问题,下面分别给出投标者后悔心理行为刻画、拍卖模型构建以及最优投标策略确定的描述。 在实际拍卖过程中,投标者并非是完全理性的[17],其不仅关心获胜的期望收益,而且关心选择不同投标策略时可能产生的相对效用,即投标者预期后悔[18]。在这种不确定的决策环境下,相对效用值通常可以通过不同方案之间的比较来测量[19],即投标者在投标获胜时的投标价与可能的次高价之间的差值,或者其投标失败时的投标者价值与可能的获胜价之间的差值。为了便于分析,下面给出投标者Ai的获胜者后悔函数RW(ΔvW)和失败者后悔函数RL(ΔvL)构建过程的描述。 由上述获胜者后悔行为和失败者后悔行为的描述可知,获胜者后悔将对投标者获得的期望效用大小产生影响,而失败者后悔将对投标者的最终获胜状态产生影响[8]。在现实拍卖中,投标者通常更关注于自己的获胜状态,也就是说,相对失败者后悔而言,投标者对获胜者后悔的预期感知并不敏感[10]。因此,这里考虑采用已有的线性后悔函数刻画投标者的获胜者后悔心理行为[7],即 RW(ΔvW)=αΔvW ΔvW=z-bi 其中,ΔvW为次高价与投标者获胜价的差值,且ΔvW≤0;α为投标者获胜的后悔参数,0≤α≤1,且α越大,表示投标者预期的获胜者后悔程度越大。 RL(ΔvL)=1-exp(-βΔvL) ΔvL=z-vi 其中,β为投标者失败的后悔参数,0≤β≤1,且β越大,表示投标者预期的失败者后悔程度越大[25]。失败者后悔函数RL(ΔvL)的示意图见图1,由图1可知,随着β值的增大,|RL(ΔvL)|也随之增大,且|RL(ΔvL)|增大的变化比例明显大于|ΔvL|增大的变化比例。 图1 失败者后悔函数RL(ΔvL)Figure 1 The Loser′s Regret Function RL(ΔvL) 为了构建考虑投标者后悔行为的一级密封拍卖模型,做出如下假设。 假设1 拍卖者不设置保留价; 假设2 在拍卖过程中,投标者Ai存在预期后悔心理行为,且其对于获胜者后悔是风险中性的,而对于失败者后悔是风险敏感的[10],除Ai外的其他(n-1)个竞标者是风险中性的[26]; 假设3 投标者Ai预期后悔心理行为对其事前期望效用的影响与后悔值的大小成反比,即在投标者获胜收益一定时,后悔值越大,则投标者的事前期望效用越小,反之亦然; 假设4 除Ai外的其他(n-1)个竞标者的估价被视为私人信息,且相互独立。同时,估价是对称的,即其他(n-1)个竞标者的估价在某一区间内服从同一概率分布,其分布函数记为G(·)。 这里需要指出的是,依据经典拍卖理论可知[27],假设1与传统拍卖假设一致;一级密封拍卖的行为实验表明[7],投标者在投标过程中存在后悔心理行为,并且相对于获胜者后悔,投标者对于失败者后悔更敏感,依据实际投标情况可知,假设3意味着投标者的期望效用与自身的后悔心理行为有关,因此假设2和假设3是合理的;某些拍卖物品并不存在确定的价值(如式样唯一的手工艺品),其对每个投标者的价值都不相同,投标者的报价只依赖于自身对于此拍卖物品的估价[28],因此假设4不仅满足独立私人估价条件,而且符合拍卖实际。 F(bi)] i=1,2,…,n (1) 进一步地,(1)式可以被简化为 (2) (2)式就是本研究建立的考虑投标者后悔心理行为的一级密封拍卖模型。在模型(2)式中,分布函数F(z)与其他(n-1)个竞标者的估价分布函数G(v-i)相关,在关于最优投标策略的研究中,通常假设v-i服从[0,1]范围内的均匀分布[8],即G(v-i)=v-i。在一级密封拍卖环境下,每个投标者仅根据自己的私人信息对拍卖品进行估价,与其他竞标者的私人信息无关,因此,有限个投标者的估价在某个区间内拥有相同的概率,即假设其他(n-1)个竞标者的估价服从均匀分布符合拍卖实际。此外,投标价与估价(投标者价值)之间存在增函数关系[29],为了便于分析,这里考虑其他(n-1)个竞标者的投标价b-i与v-i之间呈线性正比关系,令θ为相关性系数,则存在b-i(v-i)=θv-i,显然b-i(v-i)∈[0,θ]。若记x为n个投标者中的任一投标价,则关于x的分布函数F(x)可以写成 F(x)=P(z≤x)=P(θv-i≤x)n-1 (3) 针对模型(2)式,可以确定最优投标策略,即贝叶斯-纳什均衡投标策略[30],为此,有如下结论。 证明:依据bi的取值范围,下面就3种情况分别讨论投标者Ai的最优投标策略。 (1)当bi≤0时,意味着其他(n-1)个投标者给出的投标价均不低于投标者Ai的投标价,即投标者Ai投标失败,则Ai的获胜概率为0,因此,Ai在投标前仅能感知到失败者后悔。在这种情况下,由(2)式表示的投标者Ai期望效用可变为 (4) 由(4)式可知,期望效用与投标价bi无关,且在现实中bi是非负的,因此可将bi=0视为期望效用最大化时的投标价,即投标者Ai选择不参与竞拍是占优策略。 (2)当bi≥1时,意味着投标者Ai给出的投标价大于或等于其他(n-1)个投标者所给出的投标价,即投标者Ai获胜,则Ai的获胜概率为1,其投标获胜收益为(vi-bi),因此,投标者Ai在投标前会产生获胜者后悔预期。在这种情况下,由(2)式表示的投标者Ai期望效用可变为 (5) 若将(3)式代入(5)式,则(5)式可变为 (6) (3)当bi∈(0,1)时,意味着投标者Ai投标可能获胜也可能失败,在这种情况下,投标者Ai的期望效用是由(2)式所表述的。若将(3)式代入(2)式,Ai的期望效用函数可表示为 vi)]}zn-2dz (7) (8) 为方便起见,(8)式可以写成 (9) (10) 由(10)式可推导出:当如下不等式 (11) 根据定理1,可得到如下5个推论。 推论1 投标者的最优投标策略为获胜者后悔参数α的减函数,且为失败者后悔参数β的增函数。 针对(8)式两边分别对α求导,可得 故投标者的最优投标价为获胜者后悔参数的减函数。 类似地,针对(8)式两边分别对β求导,可得 故投标者的最优投标价为失败者后悔参数的增函数。证毕。 推论2 当bi∈(0,1)时,由(8)式可以看出,投标者Ai关于最优投标策略bi的确定不仅与投标者价值vi有关,而且与描述投标者心理行为的后悔参数α和β有关。 推论3 在考虑投标者是完全理性的情况下,即投标者后悔值R(Δv)=0(α=β=0),由(8)式可知投标者Ai的最优投标策略为 这一结果与VICKREY[27]得到的风险中性纳什均衡投标策略(RNNE)相同,推论3意味着本研究的拍卖模型能够推广到完全理性的假设条件下,即完全理性投标策略是考虑后悔行为的投标策略的特例。 由(8)式可以看出,后悔参数α和β对最优投标策略是有影响的,并且后悔参数的确定取决于投标者的投标者价值和投标价。在投标者价值既定的情况下,投标者的投标价通常可以通过实验方法来确定[31]。因此,为了确定后悔参数,这里给出获取投标者投标价的实验方法,该实验方法是一个拍卖模拟实验方法。为了进行拍卖模拟实验,可事先运用面向对象的程序设计开发一级密封拍卖系统[32]。在完成系统开发后,让参与实验的被试使用该系统进行模拟实验。具体地,参与实验的被试进入实验室后首先领取实验说明,并根据随机分配的计算机编号,找到相应机位以等待实验的进行。每个被试登陆系统后需在计算机上独立完成所有操作,在实验过程中,将采用真实的货币激励方式,付给被试一定的出场费;此外,如果被试严格按照实验要求进行投标且所提供数据均为有效数据,那么其还将会获得额外奖励。实验方法由被试、实验设计、实验程序等3个部分组成,下面分别对这3个部分给予说明。 以某一个特定的物品作为拍卖标的物进行一级密封拍卖的模拟实验,该模拟实验由一名实验组织者或实验操作者组织完成。在实验过程中,选取40名被试参与模拟拍卖实验,并要求被试事先了解拍卖和投标的相关知识,并熟悉该标的物的拍卖过程。 本研究的实验设计参照ENGELBRECHT-WIGGANS et al.[8]针对考虑投标者心理行为的投标策略研究中给出的实验设计,依据实验组织者对被试提供或不提供获胜者和失败者后悔反馈信息,设计如下4种实验条件。 实验条件1 拍卖组织者对被试不提供其投标获胜时的次高价信息和投标失败时的获胜价信息; 实验条件2 拍卖组织者对被试提供其投标获胜时的次高价信息,不提供其投标失败时的获胜价信息; 实验条件3 拍卖组织者对被试提供其投标失败时的获胜价信息,不提供其投标获胜时的次高价信息; 实验条件4 拍卖组织者对被试提供其投标获胜时的次高价信息和投标失败时的获胜价信息。 针对上述每个实验条件,均要求随机选择10个被试参与拍卖模拟实验,且每个被试仅在一种实验条件下进行拍卖模拟实验。 实验程序主要由实验操作和参数确定两部分组成,实验操作是指拍卖模拟实验的具体操作要求和实验过程,参数确定是指依据通过实验获取的数据并运用计算公式来确定具体的后悔参数值。 5.3.1 实验操作 在实验前,事先设定5个较大的投标者价值取值水平(如50、60、70、80、90,这里投标者价值的最大取值设定为100)。实验中,要求每个被试在每个设定的投标者价值取值水平下,依据自身对标的物的心理出价水平重复投标20次,但要求被试的出价水平不能高于设定的投标者价值,这样,一个被试共需要进行100次投标出价决策;在每一次投标过程中,设计每个被试与两个计算机模拟投标者竞标(即n=3),实验组织者将告知被试,计算机模拟投标者采取的是使其预期收益最大化的投标策略(即纳什均衡投标策略),但具体投标价对于被试是未知的,从而为所有被试创造一个相同的信息环境。本实验为被试提供了一个大量拍卖的环境,这样能使被试进一步理解自身投标决策对拍卖结果的影响,从而在进行每次投标出价决策之前会更加慎重,同时通过重复实验也能够使被试加速学习。下面给出实验操作中的两点说明。 (1)实验前事先设定5个较大投标者价值取值水平的原因在于:一方面,拍卖中投标获胜者通常具有较大投标者价值,通过设定较大的投标者价值,能够更加明确后悔心理行为对拍卖结果的影响;另一方面,具有较小投标者价值的投标者,通常意味着其投标价也相对较低,这样其投标获胜的概率就会较小,继而一些投标者将不认真进行实验,从而对实验产生干扰数据。因此,设定较大的投标者价值能够很好地避免干扰数据的产生。 (2)实验中,设计每个被试与两个计算机模拟的竞争对手竞标的原因在于:首先,是能够有效消除其他外源变量(如相互勾结、围标等)的影响;其次,利用计算机模拟投标者能够满足与被试竞标的其他投标者是风险中性和独立估价的假设。 5.3.2 后悔参数确定 (12) (13) 为了说明上文给出的考虑投标者后悔心理行为的一级密封拍卖最优投标策略确定方法,这里给出确定SO2排污权拍卖的最优投标策略的一个实例。 SO2排污权交易或拍卖在中国的发展还处于起步阶段[33],排污权拍卖是应用经济手段优化环境容量资源配置、控制环境污染的一种新型的环境政策[34],是控制企业排污量、预防环境污染的一种有效措施[35]。在排污权交易中,政府环境监管部门依据对环境的监测和环境质量目标,推算出环境允许污染物的最大排放量,并将最大排放量划分为若干规定的排放量,通常称为若干的排污权,政府可将一定比例的排污权进行拍卖交易[36],而不同的企业可根据自身实际利益和对环境的污染程度决定是否买入相应的排污权[37]。由于企业对于排污权的估价是与自身的治污能力相关的,所以不同企业对于排污权的估价和出价是不同且相互独立的,并且每个企业是密封投标的,因此可将此种交易机制视为一种一级密封拍卖交易机制。这里,考虑中国东北地区S市政府拟将SO2排污权按一级密封价格拍卖方式向该地区的n个厂商进行暗标拍卖,即要求各厂商根据自身对于排污权的估价将其报价写下来装入信封,以密封的形式交给政府,最高投标价者将获得排污权并支付其投标价。环境监管部门在对S市SO2排污权交易市场调查研究后,发现共有15个厂商准备参与投标。假设厂商(投标者)Ai以外的其他14个厂商对排污权估价的累积分布函数为G(v-i)=v-i,投标价范围为[0,1](单位:10万元/吨);投标者Ai对于排污权的估价为0.800/10万元/吨。这里,考虑如何确定投标者Ai的最优投标策略,首先进行投标者的后悔参数的确定,然后通过求解拍卖模型确定最优投标策略。 根据上文给出确定后悔参数的实验方法,这里针对SO2排污权拍卖为实际背景进行模拟实验,以便确定影响SO2排污权拍卖最优投标策略的后悔参数值。下面简要给出模拟实验的相关说明。 (1)实验环境 在实验之前,通过雅奇MIS设计开发了专用的一级密封拍卖系统[38],利用Access 2003存储数据。本次实验在东北大学工商管理学院实验室进行,被试为40人,均为该学院管理科学与工程专业的博士研究生和硕士研究生,男生22人,女生18人,年龄在22岁~27岁之间(M=23.760,SD=1.360)。被试进入实验室后首先领取实验说明(见附录A),并根据随机分配的计算机编号找到相应机位,然后按照实验说明在一级密封拍卖系统中独立进行拍卖模拟实验。 (2)实验数据分析 利用最小二乘法[39]分析可知,在提供获胜者后悔反馈信息条件下平均投标价随时间而降低(p值为0.001),在提供失败者后悔反馈信息条件下平均投标价随时间升高(p值为0.005);然而,在其他实验条件下则不会出现这种情况,可见重复实验的过程也是被试逐渐学习的过程。 依据上文给出参数确定中的数据处理方法,将不同实验条件下被试的投标价进行均值规范化处理,结果见表1。由表1可知,在4种实验条件下,提供两种后悔反馈信息实验条件下的平均投标价低于提供失败者后悔反馈信息条件下的平均投标价,且高于提供获胜者后悔反馈信息条件下的平均投标价;类似地,不提供后悔反馈信息实验条件下的平均投标价同样低于提供失败者后悔反馈信息条件下的平均投标价,且高于提供获胜者后悔反馈信息条件下的平均投标价。 图2 在4种实验条件下相同投标者价值水平时的投标价与投标者价值比值的均值Figure 2 Average Bid Prices in Line with the Same Bidder′s Value under Four Different Experimental Conditions 表1 实验数据的规范化处理结果Table 1 Normalization Treatment Results of the Experiment Data 在拍卖模拟实验过程中,一些被试认为,除非他们获胜,否则他们将不会获得任何收益,而另一些被试则从获胜概率的角度认为低的投标价可能会导致错失一个以合适的价格赢得标的物的良好机会,但几乎很少有人在实验中会预期获胜者后悔的概率。因此,可以看出被试趋向于考虑失败者后悔,直到被试经历了很多次投标以后才会趋向于考虑获胜者后悔,所以投标者在提供获胜者后悔反馈信息条件下将会随着时间的推移降低投标价。同时,投标者在提供失败者后悔反馈信息条件下也会随着时间的推移提高投标价。通过图2和表1可以看出,在提供获胜者后悔反馈信息和提供失败者后悔反馈信息两种实验条件下投标价确实按着预期的方向发展。但是,如果获胜者后悔反馈信息随着时间推移有更强的影响作用,那么在提供两种后悔反馈信息实验条件下投标价则会随着时间降低,但没有在单纯提供获胜者后悔反馈信息实验条件下降低的多。 已有研究中,FILIZ-OZBAY et al.[10]认为投标者在投标之前一般会预测失败者后悔,而对于获胜者后悔一般不会预测,也不会出现明显的低投标现象。这一结论与本研究上述实验数据分析结果相一致,即被试在实验中更趋向于考虑失败者后悔,直到被试经历了很多次实验以后才会趋向于考虑获胜者后悔。因此,为了便于分析和计算,这里设定在不提供后悔反馈信息条件下,α=0;将处理后的实验数据代入(13)式可得,在不提供后悔反馈信息条件下,β=0.157。α=0的含义是投标者在不能获取与后悔相关的反馈信息情况下,其不会预期获胜者后悔;β=0.157的含义是投标者在这种实验条件下会对失败者后悔有所预期,且后悔感知程度较小。该参数估计值对制定投标策略的影响是,投标者在这种信息条件下会在一定程度上提高实际投标价。特别地,在提供失败者后悔反馈信息条件下,β′为投标者失败时的后悔参数,β′=0.549,其含义是投标者在可以得知投标的获胜价情况下,会对失败者后悔有比较高的心理预期。该参数估计值对制定投标策略的影响是,投标者在这种信息条件下会显著提高实际投标价。类似地,依据(12)式可计算得到在提供获胜者后悔反馈信息条件下,α′为投标者获胜时的后悔参数,α′=0.216,其含义是投标者在可以得知投标的次高价情况下,会对获胜者后悔有一定的心理预期。该参数估计值对制定投标策略的影响是,投标者在这种信息条件下会在一定程度上降低实际投标价。 通过本研究实验分析可知,在考虑拍卖者是否对投标者提供获胜者后悔反馈信息的情况下,投标者获胜时的后悔参数值不同;类似地,在是否为投标者提供失败者后悔反馈信息的情况下,投标者失败时的后悔参数值也是不同的。因此,针对本节给出的实例,将从提供4种不同反馈信息的拍卖机制角度进行分析计算。 (1)拍卖结束后,拍卖者对投标者除提供获胜状态外同时提供失败时的获胜价和投标者获胜时的次高价信息(即向投标者提供两种后悔反馈信息),这时投标者Ai的事前期望效用为 (14) 此时,投标者的最优投标策略为 (15) (2)拍卖结束后,拍卖者对投标者除提供获胜状态外同时提供投标者获胜时的次高价信息(即向投标者提供获胜者后悔反馈信息),这时投标者Ai的事前期望效用为 表2 针对不同实验条件和参数取值水平的非线性投标模型和线性投标模型的实验数据对比分析Table 2 The Comparative Analysis of the Non-linear and Linear Auction Model under Different Experimental Conditions and Parameter 注:相对获胜者后悔,投标者在拍卖中对失败者后悔更加敏感,在同一实验条件下参数取值设置为α≤β,参照已有研究和本研究实验得到的后悔参数值,设置获胜者后悔参数α(α′)和失败者后悔参数β(β′)分别以0.100为步长从0.000增加到0.500进行灵敏度分析。 (16) 此时,投标者的最优投标策略为 (17) (3)拍卖结束后,拍卖者对投标者除提供获胜状态外同时提供投标者失败时的获胜价信息(即向投标者提供失败者后悔反馈信息),这时投标者Ai的事前期望效用为 (18) 此时,投标者的最优投标策略为 (19) 从上述提供不同反馈信息的结果中可以看出,当提供与失败者后悔相关的获胜价信息时,投标者的最优投标价为7.660万元/吨,其投标价是最高的;当提供与获胜者后悔相关的次高投标价信息时,投标者的最优投标价为7.440万元/吨,其投标价是最低的;而同时提供与获胜者后悔相关的次高价和与失败者后悔相关的获胜价信息时,其投标价介于上述两个结果之间,为7.590万元/吨;拍卖之后不提供任何与后悔相关的反馈信息时,投标者的最优投标价为7.540万元/吨。由此可以看出,提供与失败者后悔相关的信息后,投标者的投标价确实比不提供任何后悔相关信息时的最优投标价高;而提供与获胜者后悔相关的信息后,投标者的投标价确实比不提供任何后悔相关信息时的最优投标价低。这也进一步解释了现实中出现的超投标和低投标的现象。尽管上述投标者对于SO2排污权最优投标价单位价格相差不是很大,但当考虑到具体的拍卖量时,投标者最终支付的金额会有相当大的差异,这对于投标者(厂商)来说将会是相当可观的一笔“收入”。 最后,从拍卖者的角度来说,根据上述4种不同反馈信息实验条件下产生的最优投标价的大小关系,可以选择合适的拍卖机制,通过选择为投标者提供不同的反馈信息来使自身的收益最大化。可以看出,拍卖者对投标者仅提供与失败者后悔相关的获胜价信息时能够使自身的收益最大化,这对于实际拍卖中连续拍卖机制的设计具有很强的指导意义。 本研究针对一级密封拍卖的最优投标策略确定问题,将投标者后悔心理行为与传统拍卖理论相结合,给出一种考虑投标者后悔心理行为的最优投标策略确定方法。在该方法中,分别采用线性函数和非线性函数刻画投标者的获胜者后悔和失败者后悔心理行为,并在此基础上构建综合考虑投标者预期获胜后悔和失败后悔的非线性拍卖模型,同时通过模型求解分析最优投标策略,进一步地,给出确定模型参数的实验方法,并通过一个实例分析说明本研究给出方法的潜在应用价值。 理论研究结果表明,投标者的最优投标策略不仅与投标者价值有关,而且与投标者的后悔心理行为有关;投标者的最优投标策略为获胜者后悔参数的减函数,且为失败者后悔参数的增函数;在仅考虑投标者预期获胜后悔时,最优投标策略与线性拍卖模型所得结果相同,并且将低于完全理性的最优投标策略,而在仅考虑投标者预期失败后悔时,最优投标策略将高于完全理性的最优投标策略;完全理性的最优投标策略是考虑投标者后悔行为的投标策略的特例,且当投标者人数非常多时,完全理性的最优投标策略是报出自身的真实估价。 实验研究结果表明,与线性拍卖模型比较,由非线性拍卖模型得到的最优投标策略更接近于真实投标报价,并且将非线性后悔函数引入到拍卖模型中能够较好地反映实际拍卖中投标者的心理行为。 通过本研究得到如下管理启示和现实意义。投标者在制定投标策略时,需要综合考虑自身对预期后悔的感知,特别是对失败者后悔的敏感性;拍卖组织者在拍卖机制设计时,若选择仅向投标者提供与失败者后悔相关的获胜价信息,则能够增加自身收益,而若选择仅向投标者提供与获胜者后悔相关的次高价信息,则将使自身收益减少。 本研究仅针对一级密封拍卖机制下考虑投标者后悔心理行为的最优投标策略确定方法进行研究,今后将探讨针对二级密封拍卖、组合拍卖等其他拍卖机制下的情形;另外,还可以关注不同拍卖机制对考虑投标者心理行为的最优投标策略的影响。 [1]KLEMPERER P.Auction theory:a guide to the literature.JournalofEconomicSurveys,1999,13(3):227-286. [2]王彦,李楚霖.拍卖中的串通出价.管理工程学报,2004,18(3):16-21. WANG Yan,LI Chulin.Bidding rings at second price and first price auctions.JournalofIndustrialEngineeringandEngineeringManagement,2004,18(3):16-21.(in Chinese) [3]陈剑,陈熙龙,宋西平.拍卖理论与网上拍卖.北京:清华大学出版社,2005:2-6. CHEN Jian,CHEN Xilong,SONG Xiping.Auctiontheoryandonlineauction.Beijing:Tsinghua University Press,2005:2-6.(in Chinese) [4]李建标,汪敏达,王鹏程.多物品共同价值拍卖的信息产生与效率.管理科学,2014,27(1):120-130. LI Jianbiao,WANG Minda,WANG Pengcheng.Information generation and efficiency of multi-unit common value auction.JournalofManagementScience,2014,27(1):120-130.(in Chinese) [5]汪定伟.网上拍卖的模型与机制设计.北京:电子工业出版社,2014:15-16. WANG Dingwei.Onlineauctionmodelandmechanismdesign.Beijing:Publishing House of Electronics Industry,2014:15-16.(in Chinese) [6]保尔·米格罗姆.拍卖理论与实务.北京:清华大学出版社,2006:9-15. MILGROM P.Puttingauctiontheorytowork.Beijing:Tsinghua University Press,2006:9-15.(in Chinese) [7]ENGELBRECHT-WIGGANS R,KATOK E.Regret in auctions:theory and evidence.EconomicTheory,2007,33(1):81-101. [8]ENGELBRECHT-WIGGANS R,KATOK E.Regret and feedback information in first-price sealed-bid auctions.ManagementScience,2008, 54(4):808-819. [9]ENGELBRECHT-WIGGANS R.The effect of regret on optimal bidding in auctions.ManagementScience,1989,35(6):685-692. [10] FILIZ-OZBAY E,OZBAY E Y.Auctions with anticipated regret:theory and experiment.TheAmericanEconomicReview,2007,97(4):1407-1418. [11] ENGELBRECHT-WIGGANS R,KATOK E.A direct test of risk aversion and regret in first price sealed-bid auctions.DecisionAnalysis,2009,6(2):75-86. [12] DU S,ABENDROTH L,CHANDRAN S.Bidders′ regret in auctions.AdvancesinConsumerResearch,2006,33:516. [13] ASTOR P,ADAM M,JHNIG C,et al.Measuring regret:emotional aspects of auction design∥Proceedingsof2011EuropeanConferenceonInformationSystems.Helsinki,2011:88. [14] TUROCY T L,WATSON E.Reservation values and regret in laboratory first-price auctions:context and bidding behavior.SouthernEconomicJournal,2012,78(4):1163-1180. [15] BOSSUYT E,MOORS A,DE HOUWER J.Exploring the relations between regret,self-agency,and the tendency to repair using experimental methods and structural equation modeling.ThePsychologicalRecord,2014,64(4):841-857. [16] FILIZ-OZBAY E,OZBAY E Y.Anticipated loser regret in third price auctions.EconomicsLetters,2010,107(2):217-219. [17] JIANG Z Z,FANG S C,FAN Z P,et al.Selecting optimal selling format of a product in B2C online auctions with boundedly rational customers.EuropeanJournalofOperationalResearch,2013,226(1):139-153. [18] XIA M,CHEN J,ZHANG J.Multi-criteria decision making based on relative measures.AnnalsofOperationsResearch,2015,229(1):791-811. [19] KOU G,LIN C.A cosine maximization method for the priority vector derivation in AHP.EuropeanJournalofOperationalResearch,2014,235(1):225-232. [20] BELL D E.Regret in decision making under uncertainty.OperationsResearch,1982,30(5):961-981. [21] LOOMES G,SUGDEN R.Regret theory:an alternative theory of rational choice under uncertainty.TheEconomicJournal,1982,92(368):805-824. [22] HAN B,ALESSANDRA C,ENRICO D.A quantitative measurement of regret theory.ManagementScience,2010,56(1):161-175. [23] CHORUS C G.Regret theory-based route choices and traffic equilibria.Transportmetrica,2012,8(4):291-305. [24] 张晓,樊治平,陈发动.基于后悔理论的风险型多属性决策方法.系统工程理论与实践,2013,33(9):2313-2320. ZHANG Xiao,FAN Zhiping,CHEN Fadong.Method for risky multiple attribute decision making based on regret theory.SystemsEngineering-Theory&Practice,2013,33(9):2313-2320.(in Chinese) [25] 张晓,樊治平,陈发动.考虑后悔规避的风险型多属性决策方法.系统管理学报,2014,23(1):111-117. ZHANG Xiao,FAN Zhiping,CHEN Fadong.Risky multiple attribute decision making with regret aversion.JournalofSystems&Management,2014,23(1):111-117.(in Chinese) [26] 李建标,汪敏达,王鹏程,等.风险规避与一级密封拍卖的有限腐败:模型及实验.管理科学,2011,24(4):95-104. LI Jianbiao,WANG Minda,WANG Pengcheng,et al.Risk aversion and the limited corruption in first-price sealed auctions:model and experiments.JournalofManagementScience,2011,24(4):95-104.(in Chinese) [27] VICKREY W.Counterspeculation,auctions,and competitive sealed tenders.TheJournalofFinance,1961,16(1):8-37. [28] 杜黎,胡奇英.一类网上英式拍卖:顾客投标行为研究.管理科学学报,2006,9(3):31-38. DU Li,HU Qiying.Study on bidding strategies in online auctions.JournalofManagementScienceinChina,2006,9(3):31-38.(in Chinese) [29] DANG C,HU Q,LIU J.Bidding strategies in online auctions with different ending rules and value assumptions.ElectronicCommerceResearchandApplications,2015,14(2):104-111. [30] 王明喜,刘树林,汪寿阳.带佣金率和保留价的一级和二级价格拍卖.管理评论,2012,24(3):24-32. WANG Mingxi,LIU Shulin,WANG Shouyang.The first-price and second-price auction with both commission rate and reserve price.ManagementReview,2012,24(3):24-32.(in Chinese) [31] 刘旭旺,齐微,汪定伟,等.多属性逆向拍卖分组评标行为的实验研究.数学的实践与认识,2014,44(19):40-47. LIU Xuwang,QI Wei,WANG Dingwei,et al.The experimental study of grouped bid evaluation behavior about multi-attribute reverse auction.MathematicsinPracticeandTheory,2014,44(19):40-47.(in Chinese) [32] 王书爱.面向对象程序设计的应用.电脑知识与技术,2011,7(29):7289-7290. WANG Shu′ai.The application of object-oriented programming.ComputerKnowledgeandTechnology,2011,7(29):7289-7290.(in Chinese) [33] 杨海亮.初始排污权拍卖分配方式研究.南京:南京林业大学,2014:33. YANG Hailiang.Researchontheallocationofinitialemissionpermitsauction.Nanjing: Nanjing Forestry University,2014:33.(in Chinese) [34] 刘亚沛.陕西省二氧化硫排污权交易体系建设研究.西安:西安工业大学,2012:19-20. LIU Yapei.ResearchontradingsystemofemissionquotaofSO2inShaanxiprovince.Xi′an:Xi′an Technological University,2012:19-20.(in Chinese) [35] 汪星,陶长琪,唐国吉.基于环境约束和要素集聚因素下的企业间博弈分析.管理科学,2014,27(4):51-58. WANG Xing,TAO Changqi,TANG Guoji.Analysis of firms games under the influence of environmental constraints and factor agglomeration.JournalofManagementScience,2014,27(4):51-58.(in Chinese) [36] 陈德湖.基于一级密封拍卖的排污权交易博弈模型.工业工程,2006,9(3):49-51. CHEN Dehu.Bidding game model of tradable emission permits based on first-price sealed auction.IndustrialEngineeringJournal,2006,9(3):49-51.(in Chinese) [37] 陈德湖,徐大伟.排污权拍卖理论研究综述.经济问题探索,2011(8):170-174. CHEN Dehu,XU Dawei.A review of auction theory of emission permits.InquiryintoEconomicIssues,2011(8):170-174.(in Chinese) [38] 王韬,许评.基于数据挖掘的税收决策支持系统设计.管理科学,2003,16(1):56-60. WANG Tao,XU Ping.The frame of tax decision supporting system based on data mining.JournalofManagementScience,2003,16(1):56-60.(in Chinese) [39] 冯力.回归分析方法原理及SPSS实际操作.北京:中国金融出版社,2004:23-29. FENG Li.PrincipleofregressionanalysismethodandactualoperationsofSPSS.Beijing:China Financial Publishing House,2004:23-29.(in Chinese) 附录A:实验说明 (1)实验概要 您将参加一个关于SO2排污权的拍卖模拟实验。如果您按照本实验说明并进行投标决策,那么依据您的良好实验结果,得到相应的货币奖励。在实验过程中,如果有问题可以随时举手提问,届时实验操作者会及时回答您所提出的问题。在实验室操作过程中,请不要相互交谈,独立进行实验。 在实验过程中,您将会与计算机模拟的两个投标者进行投标,即共有3个投标者。计算机模拟的投标对手将采取使其期望收益最大化的策略进行投标,整个实验您需要进行100次投标出价决策。实验桌上有一张实验表格,需要您在每次投标出价之后将实验结果填入相对应的实验表格(见附表1)。 附表1要求被试填写的实验数据表格 Appendix1TheExperimentalFormRequiredtoBeFilledinbySubjects 投标次数获胜收益获胜者后悔失败者后悔12︙99100 (2)如何获得收益 在每次投标决策开始时,系统会自动显示您本次投标决策的投标者价值(单位:千元/吨)。同时,计算机模拟的竞争对手的投标者价值由系统自动随机产生,并服从[0, 100]的分布,所有投标者的投标者价值是相互独立的,计算机模拟的竞争对手的投标策略(即如何出价)是由系统事先设定的,不会受到您投标决策的影响。 对于本次关于SO2排污权拍卖模拟实验的投标者价值(单位:千元/吨)有50、60、70、80、90共5个取值水平,每个投标者价值会连续循环20次,在这20次投标决策中,您的投标者价值是不变的,唯一变化的是计算机模拟投标者的投标者价值和投标价,以上5个投标者价值的顺序不是固定的,是由计算机随机产生的。在每一次投标决策中,您的投标者价值和输入的投标价会与计算机模拟的竞争对手进行博弈,在博弈的过程中,竞争对手的投标者价值和投标价是变化的。因此,请慎重确定您的投标价,本实验规定您输入的投标价应该大于零且不超过您的投标者价值。您获得收益的方式是赢得SO2排污权。 (3)拍卖实验系统的操作说明 本实验条件下主要包括输入界面、确认界面和结果反馈界面3个操作界面,即分别用来进行投标价的输入、投标信息的确认、投标结果的反馈。 在“输入界面”显示相关控件的意义和操作说明如下。 投标者价值:系统会自动显示您本次投标决策的投标者价值; 清空按钮:完成数据指针的动态移动,实现投标者价值的动态改变(注:再次进入输入界面需点击该按钮); 请输入您的投标价:在此编辑框输入您的投标价; 更改投标价:更改已输入的投标价; 确认投标:确认本次投标决策。 在点击“确认投标”之后进入“信息确认界面”,在该界面同样显示了相关信息和操作要求,具体如下。 投标者价值:与输入界面的投标者价值相同; 您已输入的投标价:显示您在输入界面所输入的投标价; 如果获胜,您的收益:投标获胜时您的收益来自投标者价值与投标价之间的差值; 如果失败,您的收益:投标失败时收益设定为0; 点击“确认信息”按键之后进入“信息反馈界面”,该界面上显示本次投标决策的信息如下。 获胜状态:是或否; 收益:投标者价值-投标价; 获胜价:所有投标者中最高投标价; 次高价:所有投标者中第二高投标价; 获胜者后悔:当您投标的获胜状态为“是”时,次高价与您的投标价之间的差值; 失败者后悔:当您投标的获胜状态为“否”时,获胜价与您的投标者价值之间的差值,反映了您错失了一个以合适的投标价赢得该虚拟资产的良好机会。 点击“继续投标”按钮,在关闭确认界面和结果反馈界面的同时回到输入界面,进行下一次投标决策循环试验。 附录B:实验数据 4种实验条件下被试针对设定的投标者价值水平的平均投标价分别见附表2~附表5。 附表2 实验条件1下被试针对设定的投标者价值水平的平均投标价 附表3 实验条件2下被试针对设定的投标者价值水平的平均投标价 附表4 实验条件3下被试针对设定的投标者价值水平的平均投标价 附表5 实验条件4下被试针对设定的投标者价值水平的平均投标价 OptimalBiddingStrategyinFirst-priceSealedAuctionConsideringtheBidder′sRegret GAO Guangxin,FAN Zhiping School of Business Administration, Northeastern University, Shenyang 110167, China Numerous experimental studies have shown that the bidders usually exhibit the anticipated regret psycological behaviors in first-price sealed auctions and such behaviors will have impacts on the final bidding strategies. Thus, how to determine the optimal bidding strategy with consideration of the bidder′s anticipated regret is a noteworthy topic. For the problem of the optimal bidding strategy in first-price sealed auction, a linear function and a non-linear function are adopted to describe the winner regret with respect to paying much higher price than the second highest bid price and the loser regret with respect to missing opportunities to win at a favorable price respectively. On such bases, a non-linear auction model is constructed. Then, the optimal bidding strategy is analyzed based on the above model. Further, an experimental method is carried out to determine the corresponding parameters for describing the bidder′s regret behavior. Moreover, a case study in the field of the auctions of SO2emission permits is introduced to illustrate the feasibility and its potential application of the study. Through the theoretical analysis, we find that the optimal bidding strategy is related to not only the bidder′s value but also the bidder′s regret, which bridges the gap between the bidding strategy and the bidder′s psychological behavior. The optimal bidding strategy is the descending function of the winner regret parameter and the increasing function of the loser regret parameter. In addition, when the bidder′s regret behavior is not considered, the optimal bidding strategy is the same as the one under the perfect rationality. It means that the optimal bidding strategy under the perfect rationality is a special case of the one determined by the non-linear auction model. In particularly, when the number of bidders is large enough, the optimal bidding strategy under the perfect rationality is just the bidder's true value. In the situation where the winner regret is considered only but the loser regret is ignored, the optimal bidding strategy is the same as the one determined by the linear auction model and is lower than the one under the perfect rationality. Otherwise, the optimal bidding strategy is higher than the one under the perfect rationality. Compared with the optimal bidding strategy determined by the linear auction model, the one determined by the non-linear auction model is much closer to the real auction bid price. The non-linear auction model proposed in this paper provides guidance for determining the optimal bidding strategy in the real auction considering the bidder′s regret. first-price sealed auction;anticipated regret psycological behavior;non-linear auction model;bidding strategy;experimental method Date:June 29th, 2015 DateNovember 19th, 2015 FundedProject:Supported by the National Natural Science Foundation of China(71271051) and the Fundamental Research Funds for the Central Universities(N140607001) Biography:GAO Guangxin is a Ph.D candidate in the School of Business Administration at Northeastern University. His research interests cover bidding decision analysis and operations management. His research work was published in international journals such asKybernetesandJournalofSystemsEngineeringandElectronics. E-mail:guangxin_gao@126.com FAN Zhiping, doctor in engineering, is a professor in the School of Business Administration at Northeastern University. His research interests include management decision analysis and operations management. His research work can be referred in academic journals such asEuropeanJournalofOperationalResearch,InternationalJournalofProductionEconomicsandJournaloftheOperationalResearchSociety. E-mail:zpfan@mail.neu.edu.cn F713.359 A 10.3969/j.issn.1672-0334.2016.01.001 1672-0334(2016)01-0001-14 2015-06-29修返日期2015-11-19 国家自然科学基金(71271051);中央高校基本科研业务经费专项资金(N140607001) 高广鑫,东北大学工商管理学院博士研究生,研究方向为投标决策分析和运作管理等,曾在《Kybernetes》和《Journal of Systems Engineering and Electronics》等期刊发表论文,E-mail:guangxin_gao@126.com 樊治平,工学博士,东北大学工商管理学院教授,研究方向为管理决策分析和运作管理等,曾在《European Journal of Operational Research》《International Journal of Production Economics》和《Journal of the Operational Research Society》等期刊发表论文,E-mail:zpfan@mail.neu.edu.cn □4 拍卖模型
4.1 投标者后悔心理行为刻画
4.2 拍卖模型构建
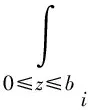
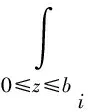



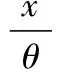
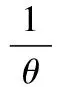
4.3 最优投标策略确定

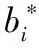
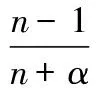
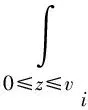
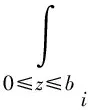

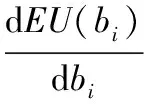

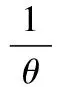
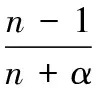
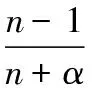
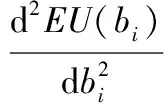
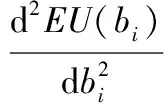
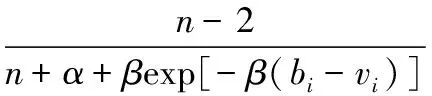
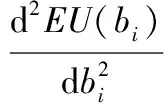

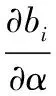
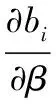
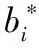
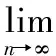
5 拍卖模型中后悔参数确定的实验方法
5.1 被试
5.2 实验设计
5.3 实验程序
6 实例分析
6.1 后悔参数的确定


6.2 参数分析
6.3 最优投标策略的确定




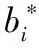
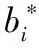
7 结论