纳米流体在板式换热器中传热特性的实验研究
孙 斌 左瑞良 杨 迪
(东北电力大学能源与动力工程学院)
纳米流体在板式换热器中传热特性的实验研究
孙 斌*左瑞良 杨 迪
(东北电力大学能源与动力工程学院)
实验使用平均粒径为50nm的Cu、Fe2O3和Al2O3纳米颗粒制备质量分数分别为0.1%、0.3%和0.5%的纳米流体,通过测量不同纳米流体的温度、流量及压力等相关参数,计算各流体在不同雷诺数下的对流换热系数和相应的熵产。实验结果表明:Cu-水纳米流体的对流换热系数相比去离子水增加的最多,Fe2O3-水次之, Al2O3-水最少;系统熵产与雷诺数的关系类似抛物线,存在最小熵产。
板式换热器 纳米流体 对流换热系数 熵产
随着科学技术的发展和能源问题的日益突出,传统的换热工质已很难满足高传热强度、微系统散热等特殊条件下的传热与冷却要求。众所周知,悬浮有固体颗粒的两相流体的换热性能明显优于传统的单相流体,然而两相流体缺乏稳定性,容易发生沉积、堵塞及磨损等不良现象,限制了它在实际生产中的应用。1995年,Choi S提出纳米流体的概念,这种流体是以一定的方式和比例在液体中添加纳米级金属或金属氧化物颗粒,形成的一类新型传热介质[1]。
近些年,国内外很多学者研究纳米流体在换热器中的传热特性,如朱建军等测量了水平微细圆管内蒸馏水和不同质量浓度的多壁碳纳米管纳米流体在低雷诺数下的强制对流换热特性[2]。李金凯等采用瞬态热线法测量了SiO2和SiO2-乙二醇两种纳米流体在不同体积分数和温度下的导热系数,分析研究了纳米SiO2体积含量、温度和悬浮稳定性对纳米流体导热系数的影响[3]。研究发现将碳纳米管(CNT)[4]、A12O3[5]及CuO[6]等纳米颗粒加入水、醇、油之后,传热系数较原基液有了明显提高。宫玉英等利用两步法制备了体积分数为0.2%~2.0%的SiO2-水纳米流体,实验结果表明:SiO2-水纳米流体在热管内具有良好的等温性能[7]。韩建荒等在对大型翅片管式换热器结构合理简化的基础上,应用CFD和数值传热学方法建立了翅片管式换热器内部流动与传热的数学模型,得到了其内部流场和温度场的分布规律[8]。倪振伟等提出以换热器的总熵增率作为换热器的经济性指标[9,10]。余敏等分析了换热器特性参数与热力性能熵产[11]。林红良等揭示了换热器能耗产生的原因,确定了最佳的热力参数匹配[12]。柳雄斌等以“仅以传递热量为目的”和“参与不可逆布雷顿循环”的逆流换热器为例,比较了熵产极值准则和火积耗散极值准则在换热器参数优化问题中的适用性[13]。对参与热功转换的换热器,换热器的热力学优化准则取为熵产极值较好。
本课题组将高效传热工质——纳米流体和高效传热设备——板式换热器整合到一个传热实验系统中,对流体的对流换热特性进行研究并计算板式换热器的熵产,希望能找到纳米流体最经济适用的应用途径,获得换热器能效最高的工况,促进我国节能减排事业的深入开展。
1 实验系统
纳米流体流动与对流换热性能的测试一般采用稳态法,实验装置是一个流动循环系统,主要由储液装置、循环动力系统、加热装置、数据采集装置、冷却系统及换热器等组成(图1)。实验主要由两条循环回路完成,冷水回路:储液罐中的纳米流体→泵1→流量控制阀→板式换热器→流量计→冷却水箱→储液罐。热水回路:热水箱→泵2→板式换热器→热水箱。

图1 实验系统示意图
1.1实验装置
储液罐由有机玻璃制成,用来储存纳米流体,同时方便观察实验中纳米颗粒的悬浮状态。从冷却水箱进口流入冷却用水,并将冷却铜管呈蛇形布置,以便充分冷却,维持恒定的纳米流体入口温度。主流路中的闸阀用作总开关。流量控制阀用于控制实验系统中纳米流体的流量。实验系统中的连接管路均为内径10mm、壁厚1mm的紫铜管。为了消除沿管壁轴向的传导热损失,铜管进出端皆用塑料套管与管路相连,并在连接处用密封胶密封;为了消除热量向环境扩散,铜管外套黑色橡胶保温管并包裹铝箔胶带。为了消除入口效应的影响,使实验管内纳米流体处于充分发展区,在换热器冷进入口前300mm处增设一个长200mm的预热段,预热段管壁外以螺旋状均匀缠绕带有绝缘瓷碗的镍铬电阻丝,电阻丝直径为1.2mm,通直流电对管内纳米流体进行加热。为防止高温发生意外,在电阻丝外包裹耐火材料;在管壁外层包裹硅酸铝保温材料和铝箔胶带,防止热量散失并起保温、绝缘作用。预热段中,紧贴管壁安装温控器,实验时设定温度的上、下限,实现智能温度控制,预热段剖面图如图2所示。

图2 预热段剖面图
实验段安装8个Pt100热电阻,分别测量换热器冷进、冷出、热进、热出和管壁温度。热水箱内有电加热棒,为实验提供稳定的热源;冷却水箱内有循环冷却水,用于保持纳米流体入口温度恒定。数据采集系统相关设备参数见表1。

表1 实验设备参数
钎焊板式换热器购于广州热尔热工设备有限公司,型号为BRQ035-20,参数如下:
换热面积 0.7m2
换热片数 20
板片材料 304不锈钢
质量 4.2kg
板片厚度 0.6mm
工作压力 3.0MPa
板间距 2mm
1.2实验流程
组建实验台,集备平均粒径为50nm的Cu、Fe2O3、Al2O3纳米颗粒和去离子水,并对系统进行气密性检测与校核;用两步法制备质量分数分别为0.1%、0.3%和0.5%的纳米流体,搅拌30min,超声波震荡60min;为热水箱中的加热棒通电,同时打开与之相连的温控器,启动数据采集系统,监测水箱温度;待热水升至设定温度后,启动冷却水系统,检查各管道阀门;实验阶段,启动泵1、2,同时启动预热装置,待监测点的温度、压力及流量等稳定后,采集数据,然后改变流量,测量同一质量分数的流体在不同流量下的实验数据,重复此过程;为将实验误差控制在允许范围内,避免各组实验相互影响,在更换不同质量分数的纳米流体进行实验前,应使用去离子水冲洗实验系统,再用打气筒将去离子水打出,多次操作,并再次检查气密性;最终进行数据处理。
1.3实验装置校核
在实验开始之前,应对实验装置进行检测,验证装置的精确度。装置校核方法是测量去离子水在湍流状态下的管内对流换热系数,将实验结果与Dittus-Boelter实验关联式进行比较。将去离子水在湍流状态下所得的实验结果与运用理论公式(Nu=0.38Re0.8Pr0.3)所得的结果进行比较,由图3可知,实验结果与计算结果有较好的吻合度,误差较小,总体误差基本控制在4%左右,实验装置精度要求合格。

图3 纯水实验值与Dittus-Boelter公式计算值比较
2 实验数据处理
2.1对流换热系数
实验采用对流传热的基本计算式即牛顿冷却公式:
q=h×(tw-tnf)
式中h——对流换热系数,W/(m2·K);
q——实验段的平均热流密度,W/m2;
tw——管壁温度,℃;
tnf——纳米流体温度,℃。
其中:
q=Q/S
Q=Cnf×qm×ΔT
ΔT=Th,in-Th,out

式中Cp——纳米颗粒的比热容,J/(kg·℃);
Cbf——基液的比热容,J/(kg·℃);
Cnf——纳米流体的比热容,J/(kg·℃);
Q——实验段的加热平均热流量,W;
S——实验段有效换热面积,m2;
Th,in——换热器热进温度,℃;
Th,out——换热器热出温度,℃;
ρp——纳米颗粒的密度,kg/m3;
ρbf——基液的密度,kg/m3;
φ——纳米流体的浓度。
水的比热容比纳米颗粒的比热容大,随着纳米颗粒质量分数的增加,纳米流体整体的比热容呈减小趋势。纳米流体的平均质量流量qm为:
qm=qv×ρnf
ρnf=(1-φ)ρbf+φρp
式中qv——纳米流体的体积流量,m3/h;
ρnf——纳米流体的密度,kg/m3。
由于纳米颗粒的体积通常难以精确测定,因此纳米流体中的粒子体积份额可根据粒子的质量百分比计算,即:

式中ω——纳米流体的质量分数。

式中Tc,in——换热器冷进温度,℃;
Tc,out——换热器冷出温度,℃。
一定尺寸的纳米流体,其导热系数的计算式为:
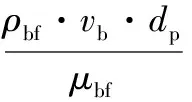

式中CB——Boltzmann常数,取1.38066×10-23J/K;
dp——纳米颗粒的平均粒径,m;
Kbf——基液的导热系数,W/(m·K);
Knf——纳米流体的导热系数,W/(m·K);
Kp——纳米颗粒的导热系数,W/(m·K);
Pr——基液的普朗特数;
Red——纳米颗粒的雷诺数;
vb——纳米颗粒的布朗速度,m/s;
μbf——基液的运动粘度,Pa·s。


2.2熵产
换热器中的总熵产Sgen,T由两部分组成:
Sgen,T=Sgen,t+Sgen,f
其中:
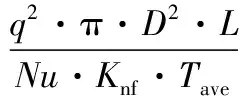

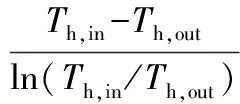
f=[0.79·ln(Re)-1.64]-2
式中f——系统的摩擦因子;
Sgen,t——由温差引起的熵产,W/K;
Sgen,f——由流动阻力引起的熵产,W/K;
Tave——换热器进口与入口的平均温度,℃;
Nu——纳米流体的努塞尔数。
3 实验结果分析与讨论
3.1对流换热系数
流体的对流换热系数是一个宏观的物理量,用来描述流体在流过温度不同的固体表面时的换热能力。以一组去离子水实验作为对比实验,分析不同质量分数相同纳米流体的对流换热系数与雷诺数关系(图4)和相同质量分数不同纳米流体的对流换热系数与雷诺数关系(图5)。
由图4、5可知,与去离子水相比,加入纳米颗粒后流体的对流换热系数有所提高,比较同种纳米颗粒流体,对流换热系数随纳米颗粒质量分数的增加而增加;比较不同纳米颗粒流体,就对流换热系数而言,Cu-水纳米流体增加的最多,Fe2O3-水次之,Al2O3-水最少。表2列出了纳米流体对流换热系数的增长情况。
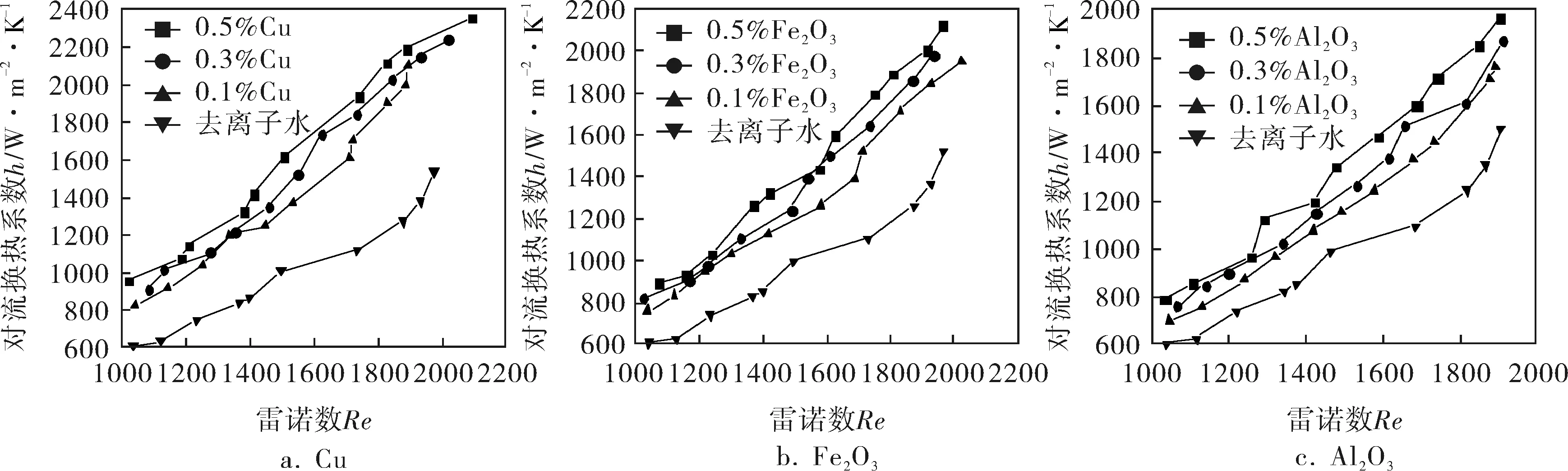
图4 不同质量分数相同纳米流体的对流换热系数与雷诺数关系

图5 相同质量分数不同纳米流体的对流换热系数与雷诺数关系

表2 纳米流体对流换热系数增长率
3.2熵产
根据相关实验数据计算换热器的总熵产,得到换热器总熵产与雷诺数的关系如图6所示。由图6可知换热器对流换热过程的总熵产随管内纳米流体雷诺数Re的变化关系:换热器的熵产图总体类似抛物线,且总熵产随着Re的增大,先减小后增大,都存在一个Re对应着最小的熵产,即最小的不可逆损失。究其原因可知,在低Re下,温差引起的熵产的影响大于流动阻力引起的熵产;而在高Re下,则是流动阻力引起的熵产占主导地位。换热器是不可逆损失较为集中的热力系统,强化传热的过程能使传热效能提高,减小温差引起的熵产,同时会使流动阻力引起的熵产增加,因此应考虑系统的总熵产,比较强化传热前后的总熵产,如果强化传热后总熵产减小,则才算达到强化传热的目的。

图6 换热器总熵产与雷诺数的关系
4 结束语
笔者用两步法制备3种纳米流体,通过实验研究了纳米颗粒种类、浓度对纳米流体在板式换热器中对流换热特性的影响。研究结果表明:当纳米颗粒种类相同时,纳米颗粒的浓度对纳米流体的对流换热系数影响较大,随着浓度的增加,不同种类的纳米流体的传热系数均有增加;当纳米颗粒的浓度相同时,相比去离子水来说,Cu-水纳米流体的传热系数增加最多,Fe2O3-水次之,Al2O3-水最少。通过对纳米流体在板式换热器中的熵产的研究发现:在低Re下,温差引起的熵产的影响大于流动阻力引起的熵产;而在高Re下,则是流动阻力引起的熵产占主导地位。
[1] Choi S.Enhancing Thermal Conductivity of Fluids with Nanoparticles[J].ASME-Publications-Fed,1995,231(66): 99~106.
[2] 朱建军,王建立,李震,等.微细管碳纳米管悬浮液强制对流换热实验研究[J].工程热物理学报,2011,32(7):1211~1214.
[3] 李金凯,赵蔚琳,刘宗明,等.氧化硅纳米流体的导热性能研究[J].化工机械,2010,37(4):405~408,417.
[4] Kumaresan V,Mohaideen Abdul Khader S,Karthikeyan S,et al.Convective Heat Transfer Characteristics of CNT Nanofluids in a Tubular Heat Exchanger of Various Lengths for Energy Efficient Cooling/Heating System[J]. International Journal of Heat and Mass Transfer,2013,60:413~421.
[5] Aly W I A.Numerical Study on Turbulent Heat Transfer and Pressure Drop of Nanofluid in Coiled Tube-in-Tube Heat Exchangers[J].Energy Conversion and Management,2014,79:304~316.
[6] Sarafraz M M,Hormozi F.Convective Boiling and Particulate Fouling of Stabilized CuO-ethylene Glycol Nanofluids Inside the Annular Heat Exchanger[J].International Communications in Heat and Mass Transfer,2014,53:116~123.
[7] 宫玉英,赵蔚琳,朱保杰,等.SiO2-水纳米流体热管传热性能的实验研究[J].化工机械,2013,40(3): 302~305,405.
[8] 韩建荒,刘扬,李君书,等.翅片管式换热器传热与流场流动特性的数值模拟[J].化工机械,2013,40(3):347~350,392.
[9] 倪振伟,焦芝林.换热器的熵增计算法与总熵增率[J].工程热物理学报,1988,9(1):4~6.
[10] 倪振伟.换热器的热力学第二定律分析与评价方法[J].工程热物理学报,1985,6(4):311~314.
[11] 余敏,马俊杰,杨茉,等.换热器特性参数与热力性能熵产分析[J].热能动力工程,2007,22(4):399~403,67~68.
[12] 林红良,李志,祝广场.换热器熵产分析[J].船电技术,2012,32(z1):35~37,41.
[13] 柳雄斌,孟继安,过增元.换热器参数优化中的熵产极值和火积耗散极值[J].科学通报,2008,53(24):3026~3029.
ExperimentalStudyonHeat-transferCharacteristicsofNanofluidsinPlateHeatExchangers
SUN Bin, ZUO Rui-liang, YANG Di
(CollegeofEnergyandPowerEngineering,NortheastDianliUniversity,Jilin132012,China)
In experiments, the 50nm-sized nanoparticles (Cu, Fe2O3and Al2O3) were adopted to prepare the nanofluid which boasting of 0.1%, 0.3% and 0.5% mass fractions respectively; and through measuring related parameters like the temperature, flow rate and the pressure of different nanofluids, their convective heat transfer coefficient and corresponding entropy production under different Reynolds numbers were calculated. The experimental results show that, as compared to the deionized water, the Cu-water nanofluid has the highest convective heat transfer coefficient, then comes to Fe2O3- water nanofluid and Al2O3- water nanofluid in turn; and the system entropy production behaves in a parabola with the change of Reynolds numbers.A minimum entropy production can be seen there.
plate heat exchanger, nanofluid, convective heat transfer coefficient, entropy production
* 孙 斌,男,1972年1月生,教授。吉林省吉林市,132012。
TQ051.5
A
0254-6094(2016)02-0148-06
2015-03-16,
2016-03-10)

