两相横向流诱发换热器管束振动的研究进展*
刘宝庆 陈小阁 陈 涛 黄博林 郑毅骏
(1.浙江大学化工机械研究所;2.浙江和田化工有限公司)
两相横向流诱发换热器管束振动的研究进展*
刘宝庆1陈小阁1陈 涛2黄博林1郑毅骏1
(1.浙江大学化工机械研究所;2.浙江和田化工有限公司)
介绍了两相横向流诱发换热器管束振动的破坏形式和机理,总结了实验研究中两相横向流诱发换热器管束振动的主要影响因素及其相关计算公式,同时回顾了现阶段的一些有关两相横向流诱发换热器管束振动的实验研究和实验获得的成果。
换热器 管束振动 两相横向流 含气率 两相阻尼
管壳式换热器的壳程流体在管束间的流动冲刷会引起管束振动,在U形管处尤其明显。而换热器管束振动会引起管子的微量磨损和疲劳,增加了换热管的维修和更换费用。对于紧凑型换热器来说,换热管磨损甚至有可能使之整体报废。一般而言,纵向流诱发换热管振动的振幅较小,对管子的磨损和疲劳影响可以忽略。而目前过程工业中绝大部分换热器内部设有折流板,壳程流体在受到折流板的限制后将改变路径横向掠过管束,这比未设置折流板的轴向流更易诱发管子振动,因此横向流诱发换热管振动是流体诱发振动的主要形式。
工业中常用的换热器(如核蒸汽发生器、冷凝器)和锅炉中均存在两相流体诱发的振动,相比单相流体来说,两相流体诱发的振动更为复杂。为此,国内外研究人员从实验和工程的角度对两相流体诱发换热器振动的原因和影响因素进行了研究。基于换热器管束间的气液两相流特性,陈斌和邱锋归纳了流型、含气率及压降等因素诱发换热器管束振动的研究进展[1]。洪文鹏等介绍了基于实验结果建立的流型图、预测含气率、摩擦压降半经验公式和各种预测方法的差异[2]。笔者在分析两相横向流诱发换热器管束振动的破坏形式和机理的基础上,从两相流、含气率及两相阻尼等多个角度总结了影响两相横向流诱发换热器管束振动的因素。
1 换热器管束振动的破坏形式
换热器管束振动的破环形式主要有碰撞损伤、折流板切割、管与管板连接处泄漏、疲劳破坏及声振动等[3]。相邻的换热管之间或换热管与管板之间由于振幅较大而相互碰撞,长此以往将导致管子壁厚减薄,甚至破裂。当换热管与折流板的管孔间存在间隙时,换热管在管孔处振动时如同受到折流板的切割。换热管振动易引起管子松动,导致管子从管板连接处脱离而发生泄漏。换热管振动时受到交变应力的作用,长时间的累积会引起换热器管束疲劳。壳程中存在气体且气柱振荡产生的驻波频率与旋涡频率一致时,会引起强烈的噪声,过高的声压会损坏换热器的壳体。
图1为某冷凝器的第一块折流板与换热管的损坏情况,可以看出,强烈的振动已经导致折流板管孔处断裂,换热管受到严重磨损[4]。图2为某大乙烯装置中由管束振动引起的泄漏情况,可以看出,随着换热器的大型化和流动的高速化,振动引起换热器破坏的可能性随之增加。

图1 某冷凝器的折流板与换热管损坏情况

图2 某大乙烯装置中管束振动引起的泄漏情况
2 两相横向流诱发换热器管束振动的机理
在管壳式换热器中,相比单向流或两相轴向流,两相横向流更加常见。通过多年研究可知,两相横向流诱发振动的机理目前比较一致的观点是旋涡脱落、湍流抖振和流体弹性不稳定性[5]。
2.1旋涡脱落
通常认为,在含气率小于0.15时,两相流才存在周期性脱落的旋涡。当旋涡脱落的频率与管束固有频率相近时,管子发生共振,产生大幅度振动。单相流的旋涡脱落频率可根据斯特劳哈尔由实验得到的公式计算[6]:
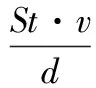
式中d——管子外径,m;
f——旋涡周期性脱落频率,Hz;
St——斯特劳哈尔数,与雷诺数Re有关的无量纲数;
v——流速,m/s。
苏新军等提出在两相流横掠错列管束诱发旋涡脱落的实验研究数据不足时,可近似应用单相流的漩涡脱落频率计算公式,其中,v是气液两相流的平均速度[7]。两相流中的斯特劳哈尔数StTP随含气率的增大而减小。
2.2湍流抖振
湍流使换热管表面的流场压力和速度产生随机性的脉动,不断供给换热管能量,当脉动的主频率接近管子的固有频率时,管子会发生强烈的振动。虽然湍流抖振引起的振动不规律,无法进行线性分析,但可以用振幅来预测振动是否会引起磨损。
2.3流体弹性不稳定性
流体弹性不稳定性一般是在其他机理(如旋涡脱落或湍流抖振)激发起管子运动的情况下产生的,它是最危险的诱发因素。动态的流体力和管子的运动相互作用,流速一旦达到临界值,极易引起大幅度振动而导致管子在支撑处被快速磨损。两相横向流的临界流速vc可用Connors提出的半经验关联式确定[6]:

式中b——指数;
f′——两相流中换热管的固有频率,Hz;
K——不稳定常数,为判定换热管是否振动的常数;
m——包括流体附加质量在内的单位管长的质量,kg/m;
ρTP——两相流的密度;
ζ——管子的总阻尼。
Pettigrew M J和Taylor C E总结了大量的实验数据后推荐[8],当节径比p/d>1.47时,不稳定常数K可取3;当节径比p/d<1.47时,不稳定常数K=4.76(p-d)/d+0.76。
3 两相横向流诱发换热器管束振动的影响因素
3.1两相流
工业用换热器和核蒸汽发生器内部的气液两相流一般是蒸汽-水,其使用环境为高温高压,对设备要求严格且成本较高,因此目前研究人员普遍选择使用空气-水、R-11(氟氯昂-11)和R-22(氟氯昂-22)代替蒸汽-水。其中,空气-水两相流最简单经济,因而,研究两相横向流诱发换热器管束振动时的工质大部分为空气-水。
表1为两相横向流诱发换热器管束振动研究中常用的4种两相流体系属性对比表[9]。可以看出,R-11和R-22的液体表面张力和运动粘度系数比空气-水的更接近蒸汽-水。而且,在液相转换为气相时,R-11需要的能量是水转换为蒸汽的8%,降低了经济成本。综合考虑,在研究两相横向流诱发换热器管束振动时,在条件允许的情况下应优先选用R-11或R-22。
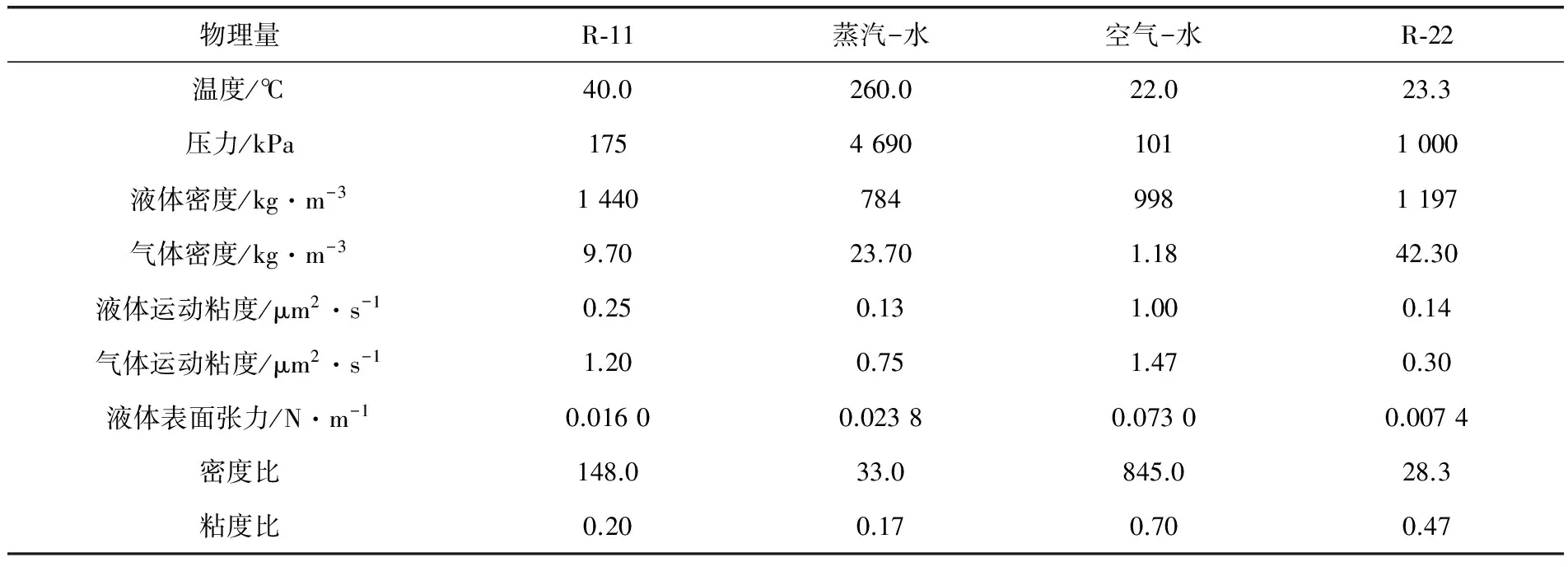
表1 R-11、蒸汽-水、空气-水和R-22的属性对比
Mitra D等分别在蒸汽-水和空气-水两相流中研究了流体弹性不稳定性诱发的管束振动,发现在低流速下,管束振幅随流速的增大而增大,蒸汽-水中的管子振幅增大速率低于空气-水,这是因为密度比越大,流速增大速度越慢[10]。而且,蒸汽-水的流体弹性不稳定性的临界流速比空气-水的低,原因是在蒸汽-水两相流中存在核状沸腾,在相变过程中管束表面的泡沫改变了换热管表面的阻力特性,由此影响了作用在管束上的流体弹性力。
Pettigrew M J和Taylor C E在R-22中研究了横向流诱发换热器管束振动,发现在相同的含气率和质量流量下,湍流在R-22中引起的激振力的振动响应低于空气-水,原因是氟利昂的表面张力和密度比明显低于空气-水[11]。
3.2含气率
Feenstra P A等提出了含气率α的一般表达式[9]:

式中S——气相和液相的速度比;
X——流体质量;
ρG——气相密度;
ρL——液相密度。
3.2.1均质流模型
均质流模型假设两相流的混合是均匀的,即S=1,这样可简化计算。在卧式换热器中,这种假设的影响不大,但在立式换热器中,由于浮力的影响较大,所以均质流模型的假设是不合理的。Pettigrew M J等使用双光纤探针法测量了立式转置三角形实验装置的含气率和流体力,并将结果与均质流模型法进行了对比,发现两相流近乎均匀,两相间的速度比可以忽略[12]。因此,由含气率计算得到的两相流密度和速度能否忽略还需要其他测量方式的进一步佐证。
3.2.2漂移流模型
辐射衰减法是漂移流模型中典型的一种含气率测量方法,其测量原理是:伽马射线的吸收量取决于两相流的平均密度。则含气率的表达式为:
α=ln(N/NL)/ln(NG/NL)
式中N——伽马射线吸收量;
NG、NL——100%气相和液相时的伽马射线吸收量。
数学核心素养主要指学生在学习时可以合理运用数学知识解决问题、思考问题,进而形成良好的学习能力、习惯与品质,为学生在日后发展奠定良好基础.
Moran J E和Weaver D S在相同的条件下,使用均质流模型和辐射衰减测量法分别测量了不同节点流速下的含气率[13]。由图3可知,同等情况下(节点质量流量Gp相同),均质流模型法得到的含气率比辐射衰减测量法得到的高,说明均质流模型法高估了两相流的含气率。

图3 均质流模型法和辐射衰减测量法测量的含气率
除上述两种方法外,梁法春等提出了基于液体取样的多相流量测量方法,即根据取样液体流量确定管路中两相流的质量含气率[14]。该方法的测量精确度和稳定性较以往有明显改善,但液体取样器与两相流诱发换热器管束振动实验仪器的配合程度有待完善。
3.2.3两相流流型
两相流流型对两相流动压力损失、传热传质特性、流动参数的准确测量和流动系统的运行特性有着不可忽略的影响。按含气率从小到大将空气-水两相流在垂直管中上升时的两相流流型(图4)分为5种:细泡型(α<30%)、气塞型(30%~50%)、块型(50%~80%)、条-环型(80%~90%)和环型(α>90%)。蒸汽-水两相流具有相同的流型[15]。

图4 空气-水两相流在垂直管中上升时的两相流流型
Ulbrich R和Mewes D通过实验研究发现,在换热器壳程流体中只存在细泡型、间歇型和弥散型[16]。贾峰等基于实验得出了流动沸腾条件下横向流冲刷管束的两相流流型,按折算速度分为泡状流、块状流和环状流[17],与文献[16]阐述的流型有较大不同。由于实验条件的限制,现阶段间歇流流型的实验数据较少,无法得出普遍性规律。
3.3两相阻尼
阻尼是流体诱发换热器管束振动的重要影响因素,当管束阻尼足够大时,可以抵抗壳程流体冲刷引起的振动。早期研究中,尽管换热器管束振动能量耗散机制可以用阻尼来解释,但由于阻尼的测定十分困难,研究人员并没有分析阻尼这一影响因素。目前,学者们提出了多种阻尼测量方式,使阻尼的测量成为可能。
3.3.1测量方法
两相阻尼的测量方法主要有半功率带宽法、对数衰减法和指数拟合法。
半功率带宽法中,阻尼ζ是频率带宽的函数,即:

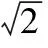
式中Amax——响应峰值;
fn——固有频率。
对数衰减法利用应变仪跟踪衰变,得到管子的响应时间后,划分为不同的部分,用各部分计算对数衰减率。当阻尼ζ小于4%时:


式中n——峰值周期数;
x1、xn——峰值;
δ——对数衰减率。
指数拟合法同样是基于管子的响应衰减用指数函数对衰减过程进行跟踪的,且在估算阻尼时能获得连续、可靠的数值。但指数拟合法拟合的敏感性不如对数衰减法。用Matlab程序拟合出一系列的峰值点得到函数y,利用该函数可计算简单谐响应的粘滞阻尼ζ:
y=Ae-Bt
B=ζωn
式中A——常数;
t——时间;
ωn——周期。
Moran J E和Weaver D S等利用辐射衰减测量法测量了含气率,并比较了不同含气率下对数衰减法和指数拟合法的阻尼值,发现对数衰减法的结果比较分散,而指数拟合法的结果相对连续[13]。原因是流体附加质量变化和两相流湍流激振的不规则响应引起频率变化,从而导致对数衰减法不可靠。指数拟合法拟合理论理想衰减曲线,因此得到的数值连续。另外,Moran J E和Weaver D S还使用均质流模型法和辐射衰减测量法测量了含气率,并比较了不同含气率下半功率带宽法和指数拟合法得到的阻尼值,发现两者得到的数据相差较小。一般,在低含气率下,半功率带宽法对频率变化更敏感,测得的阻尼变化趋势更明显。因此,半功率带宽法测量效果优于其他两种方法。
3.3.2计算方法
Pettigrew M J和Taylor C E总结了两相流的阻尼,认为在两相流中多跨度的换热管总阻尼ζT由3部分组成,分别是支撑阻尼ζS、粘滞阻尼ζV和两相阻尼ζTP[8]:
ζT=ζS+ζV+ζTP
Pettigrew M J和Taylor C E得到的半经验公式基于有限的实验数据,并不具有普适性。在无其他更优方式时可以作为参考,但需要考虑流型和两相流的影响。
3.3.3影响因素
两相流中的阻尼十分复杂,而且影响因素很多,如含气率、流速、限制因子和两相流性质。
含气率是影响阻尼的主要因素。Pettigrew M J和Taylor C E总结了两相阻尼ζTP半经验公式[18]:
ζTP∝f(α)
其中,f(α)是含气率的函数,根据含气率40%、70%可划分为3个阶段:

由图5可以看出,在正三角形、转置正三角形和正方形排列装置中,阻尼在含气率为40%~70%时有最大值[19]

图5 两相横向流中含气率与阻尼的关系
在临界流速下,流速(即质量流量)不是影响阻尼的主要因素。随着流速的增加,升力方向的阻尼小于阻力方向的。所以,流体弹性不稳定性一般发生在升力方向。
粘滞阻尼是限制因子的函数,而限制因子又是节径比p/d的函数,对于不同的管子排列方式,限制因子计算公式不同。Sim W G和Mureithi N W对比了节径比分别为1.2、1.4、1.6时的管束,发现随节径比的增大,阻尼明显下降[20]。
阻尼与两相流本身性质有关,即与两相流的表面张力密切相关,阻尼一般随表面张力的增大而增大。210℃的蒸汽-水混合物的表面张力仅为20℃空气-水混合物的一半。因此,在阻尼分析过程中,表面张力是选择两相流的重要参考因素之一。
4 结论
4.1从两相流中获得准确的含气率是研究两相流诱发振动的前提,相比于单相流诱发换热管振动,两相横向流的实验数据不多,而且大多数研究人员的实验数据都集中在含气率小于40%的范围内。而且在间歇流流型中数据比较分散,无法得出公认统一的结论,相关数据亟待补充。
4.2实验研究得出了有关阻尼的半经验公式,这些成果将为后续研究工作的展开和换热器工程设计标准的完善提供有效指导。
4.3随着换热器结构的大型化、流动的高速化和结构紧凑性的增加,流体诱发管束振动研究的热点不仅集中于两相流的流型、密度比、含气率和阻尼,相位滞后、时间滞后等影响因素也将成为新的研究视角。
4.4随着计算机技术的发展,数值模拟方法也被应用于流体诱发振动的研究中,但现在使用的数值模拟方法主要适用于空气、水等单相流,两相流模拟的有关数学模型亟需设计。
[1] 陈斌,邱锋.管束间气夜两相流动特性研究进展[J].化工机械,1999,26(2):105~109.
[2] 洪文鹏,滕飞宇,刘燕.管束间气液两相流动特性的研究进展[J].化工机械,2012,39(2):124~130.
[3] 聂清德,谭蔚.管壳式换热器流体诱发振动[M].北京:中国石化出版社,2014.
[4] Klein U,Zunkel A,Eberle A.Breakdown of Heat Exchangers Due to Erosion Corrosion and Fretting Caused by Inappropriate Operating Conditions[J].Engineering Failure Analysis,2014,43(8):271~280.
[5] 谭蔚,聂清德,段振亚.横向流中两相流体诱发的振动[J].化工设备与管道,2006,42(5):11~17.
[6] 钱颂文,岑汉钊,曾文明.换热器流体诱导振动[M].北京:烃加工出版社,1989.
[7] 苏新军,张修刚,王栋,等.气液两相流横掠错列圆柱形成旋涡脱落诱发管束振动的试验研究[J].热能动力工程,2004, 19(1):14~16.
[8] Pettigrew M J,Taylor C E.Vibration Analysis of Shell-and-Tube Heat Exchangers:An Overview——Part 1:Flow,Damping, Fluidelastic Instability[J].Journal of Fluids and Structures,2003,18(5):469~483.
[9] Feenstra P A,Weaver D S,Judd R L.Modelling Two-Phase Flow-excited Damping and Fluidelastic Instability in Tube Arrays[J].Journal of Fluids and Structures,2002,16(6):811~840.
[10] Mitra D,Dhir V K,Catton I.Fluid-elastic Instability in Tube Arrays Subjected to Air-Water and Steam-Water Cross-Flow[J].Journal of Fluids and Structures,2009,25(7):1213~1235.
[11] Pettigrew M J,Taylor C E.Vibration of a Normal Triangular Tube Bundle Subjected to Two-Phase Freon Cross Flow[J]. Journal of Pressure Vessel Technology,2009,131(5):051302.
[12] Pettigrew M J,Zhang C,Mureithi N W,et al.Detailed Flow and Force Measurements in a Rotated Triangular Tube Bundle Subjected to Two-Phase Cross-Flow[J].Journal of Fluids and Structures,2005,20(4):567~575.
[13] Moran J E,Weaver D S.On the Damping in Tube Arrays Subjected to Two-Phase Cross-Flow[J].Journal of Pressure Vessel Technology,2013,135(3):030906.
[14] 梁法春,王栋,林宗虎.气液两相流体流量或质量含气率的液体取样测量方法[J].热能动力工程,2008,23(3):256~258.
[15] 林宗虎.气液两相流旋涡脱落特性及工程应用[M].北京:化学工业出版社,2001.
[16] Ulbrich R,Mewes D.Vertical,Upward Gas-Liquid Two-Phase Flow Across a Tube Bundle[J].International Journal of Multiphase Flow,1994,20(2):249~272.
[17] 贾峰,黄兴华,王利,等.垂直向上横掠水平管束两相流型的实验研究[J].上海交通大学学报,2006,40(2):346~350.
[18] Pettigrew M J,Taylor C E.Damping of Heat Exchanger Tubes in Two-Phase Flow:Review and Design Guidelines[J]. Journal of Pressure Vessel Technology,2004,126(4):523~533.
[19] Pettigrew M J,Taylor C E,Kim B S.Vibration of Tube Bundles in Two-Phase Cross-Flow.Part 1.Hydrodynamic Mass and Damping[J].Journal of Pressure Vessel Technology,1989,111(4):466~477.
[20] Sim W G,Mureithi N W.A Two-Phase Damping Model on Tube Bundles Subjected to Two-Phase Cross-Flow[J].Journal of Mechanical Science and Technology,2014,28(2):553~563.
ProgressinResearchofTubeBundleVibrationofHeatExchangerInducedbyTwo-phaseCross-flow
LIU Bao-qing1, CHEN Xiao-ge1, CHEN Tao2, HUANG Bo-lin1, ZHENG Yi-jun1
(1.InstituteofProcessEquipment,ZhejiangUniversity,Hangzhou310027,China; 2.ZhejiangHetianChemicalCo.,Ltd.,Hangzhou310027,China)
The mode of failure and mechanism thereof of the tube bundle’s vibration in heat exchangers which
* 国家自然科学基金资助项目(201206144),中央高校基本科研业务费专项基金资助项目(2012QNA4018)。
** 刘宝庆,男,1978年10月生,副教授。浙江省杭州市,310027。
TQ051.5
A
0254-6094(2016)02-0131-07
2015-04-25,
2015-05-15)
(Continued on Page 177)

