小容积流量下汽轮机调节级动叶三维流场与级后工质温度的研究*

李 勇 王涵北

(东北电力大学能源与动力工程学院)

小容积流量下汽轮机调节级动叶三维流场与级后工质温度的研究*

李 勇**王涵北

(东北电力大学能源与动力工程学院)

以某300MW汽轮机调节级为研究对象，介绍了比例系数法和数值模拟法的基本原理。对不同相对容积流量比和不同工况下的调节级动叶三维流场进行了分析。将数值模拟方法得到的调节级级后工质温度与比例系数法、速度三角形法的计算结果进行对比，得到不同计算方法间的相对误差，并对不同相对容积流量下级后工质温度的计算方法进行了探讨。

汽轮机 动叶三维流场 级后工质温度 相对容积流量比

随着风能、太阳能等清洁能源在电力能源系统中所占比例的不断增加，要求参与调峰的大容量火电机组必须通过降低负荷，甚至是启停调峰的方式来适应新能源发电的介入。因此，火电机组的快速启停工作受到国内外学者的广泛关注。在确定火电机组启停速度和寿命损耗中，汽轮机调节级后的温度变化率对优化火电机组启停具有重要影响。为确定主蒸汽流量较小时的级后工质参数，文献[1～4]提出当汽轮机负荷低于80%额定负荷时，采用比例系数法进行参数计算，然而这种估算方法并未考虑汽轮机冲转流量变化带来的影响，必然引起调节级级后温度变化率产生较大误差。

随着CFD技术的兴起与日渐成熟，数值模拟方法在汽轮机调节级和小容积流量研究中获得了广泛应用。文献[5～7]通过模拟调节级三维流场，分析了工质经过调节级堵塞区域时通道中静压的变化情况。谢金伟等通过建立完整的调节阀至调节级段模型，对不同工况下该段的三维流动与压力损失特性进行了研究[8]。文献[9～12]对汽轮机调节级气动性能和气流激振突变方面进行了研究，提出了优化调节级结构的可行方案。文献[13,14]通过对低负荷运行的汽轮机末几级进行数值模拟，得到当容积流量小到一定程度时末级动叶会做负功的结论。张仲彬等对多级流动进行了数值分析，结果表明，小容积流量工况时上级流场的分离流动会导致下级流场内分离区域增多[15]。

目前国内外学者普遍关注的是小容积流量工况下汽轮机的末级流动状态，而调节级小容积流量方面的研究却鲜有报道。在此，笔者对不同相对容积流量比和不同工况下的调节级动叶三维流场进行分析，并将采用数值模拟方法得到的调节级级后工质温度与比例系数法、速度三角形法计算结果进行对比，得到不同计算方法间的相对误差，以指导不同容积流量下级后工质温度的计算。

1 比例系数法

比例系数法中首先根据热力特性说明书查出汽轮机额定负荷下的主蒸汽温度、压力，再进行计算：

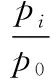
(1)

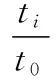
(2)

式中p0、p01——额定工况和变工况下的主蒸汽压力，MPa；

pi、pi1——额定工况和变工况下某一级特征面的蒸汽压力，MPa；

t0、t01——额定工况和变工况下的主蒸汽温度，℃；

ti、ti1——额定工况和变工况下某一级特征面的蒸汽温度，℃。

由式(1)、(2)可知，比例系数法存在两方面问题。首先，对于汽轮机冲转阶段而言，主蒸汽参数基本不变，因此该方法计算出的调节级级后工质参数也不随时间改变。而事实上，汽轮机冲转时需要调节阀全开来保证汽缸和转子受热均匀，因此多数电厂采用高压主汽阀控制汽轮机转速以便进行低速检查和中速暖机，这就使主汽阀开度在冲转阶段随时间变化，进而引起调节级入口、出口工质参数随时间改变。其次，式(1)、(2)中没有体现冲转流量改变对调节级级后工质参数的影响。

2 物理模型和数值方法

2.1 物理模型

笔者对某300MW汽轮机调节级叶片及其流域进行建模，叶片几何尺寸见表1。

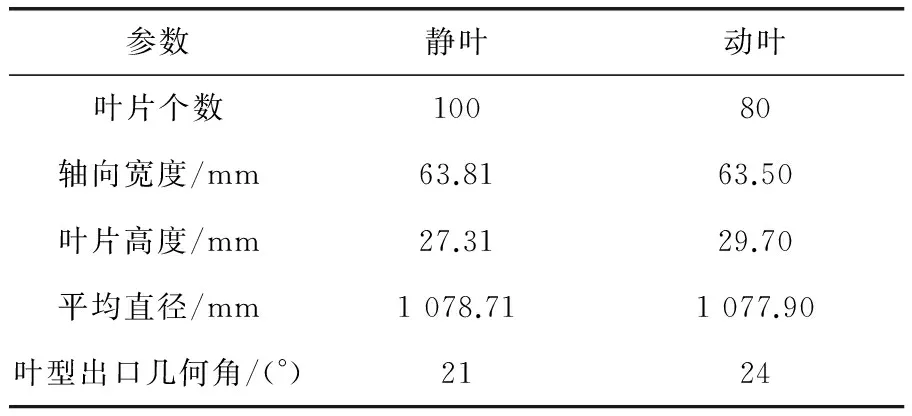
表1 某300MW汽轮机调节级叶片几何尺寸

采用Gambit软件建模时，由表1可知，调节级动、静叶片数不同，同一工况下单位静叶流道与单位动叶流道的质量流量不同，因此不能采用单叶片模型进行研究，而建立整周模型所需网格数量大，容易导致计算机内存超限并延长计算时间，经观察发现，5个静叶与4个动叶构成的流域具有相同质量流量，遂建立如图1所示的物理模型。笔者选用的调节级模型部分进汽度高达0.96，建模时可忽略其影响。

在调节阀全开的情况下，过热蒸汽通过汽轮机蒸汽室进入调节级静叶，经喷嘴加速、动叶做功后流入调节级汽室进行充分混合。为保证建立的

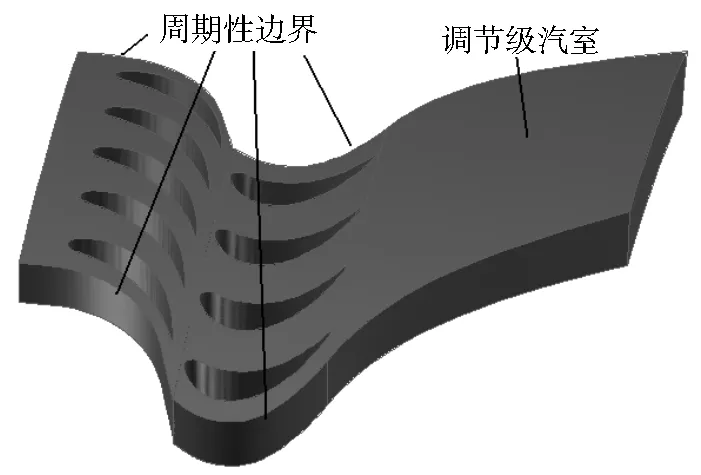
图1 某300MW汽轮机调节级物理模型

模型与实际情况相似，同时考虑到网格划分的需要，设置动叶入口截面距动叶前缘点0.2mm，动叶出口截面距动叶尾缘点0.2mm，并在动叶后建立轴向距离等于真实长度的调节级汽室模型，在保证动叶出口流体充分发展的同时使流动更加真实。汽室部分在动叶生成流域的基础上切割而成，不但提高了动叶与汽室连接处的顺滑性，也为划分高质量网格提供了保证。叶栅通道网格(结构化网格)划分情况如图2所示。

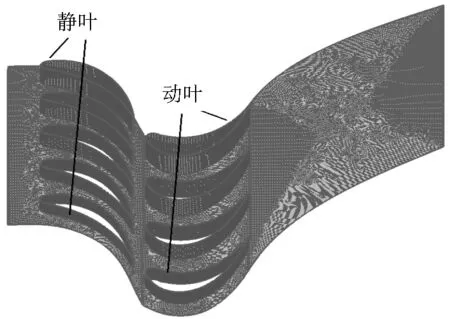
图2 叶栅通道网格划分情况

2.2 网格无关性讨论

为兼顾计算速度和准确度，笔者对模型进行了网格无关性讨论。在保证计算方法、边界条件不变的前提下，分别对网格数为184万、292万、346万、422万的模型进行数值模拟。结果表明，当网格数大于346万后，随着网格数的增加模拟结果几乎不变，故综合考虑后取346万网格的方案。

2.3 数值方法

采用Fluent软件进行计算，选择适用于参数研究的标准k-ε湍流模型，应用Simplec算法和二阶迎风离散格式，采用旋转周期性边界条件，动叶流域及其固体壁面均绕x轴以给定转速旋转，静叶、汽室流域及其固体壁面保持静止。静叶、动叶、调节级汽室三者交界面采用滑移网格技术进行数据交换。入口边界条件为压力入口，出口边界条件为质量流量出口(mass-flow inlet中的outward normals)，过热蒸汽采用相较于理想气体更接近真实水蒸气性质的Redlich-Kwong气体模型，能量方程收敛精度为10-6，速度方程收敛精度为10-3。

3 计算结果分析

3.1 动叶三维流场的分析

由文献[15]可知，当本级静叶入口工质均匀时，容积流量减小很难引起静叶流域发生明显的流动分离，故主要分析动叶三维流场的情况。为了排除汽轮机转速对流场的影响，将动叶及其流域转速均设为3kr/min。相对容积流量比k为：

k=G1v1/(Gv)

(3)

式中G、G1——阀门全开和变工况下调节级动叶出口蒸汽质量流量，kg/s；

v、v1——阀门全开和变工况下调节级动叶出口蒸汽比容，m3/kg。

以阀门全开工况为基准，图3为不同k下同一动叶流道50%叶高截面处的流线图，图4为k为0.290时同一工况下不同叶高截面处的流线图。

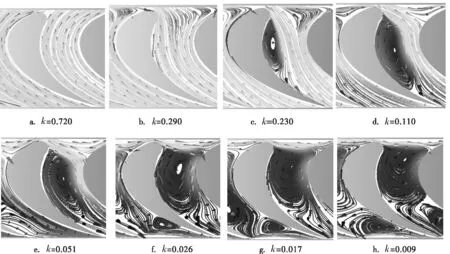
图3 不同k下同一动叶流道50%叶高截面处的流线图

图4 同一工况下不同叶高截面处的流线图

由图3可知，随着k值的减小，调节级动叶压力面前缘点附近会出现流动分离，分离区与主流之间有一条明显的分离线。出现流动分离的原因是容积流量较小时调节级静叶出口汽流绝对速度较小，由于动叶高速旋转，导致汽流以较大负攻角进入动叶流域并被吸力面分为两支，其中一支在旋转叶片的作用下沿本流道继续向下游运动，另一分支流入相邻流道并在动叶压力面附近产生漩涡。当k>0.026时，压力面漩涡轴向影响范围随k值的减小而增大，这是因为此时负攻角较大，而且容积流量相对较高，工质经堵塞段加速后具有较大的轴向分速度，使再附点逐渐远离分离点；当k<0.026时，动叶出口吸力面附近出现了流动分离且分离区随k值的减小而增大，此分离区的出现使动叶内工质横向流动明显加剧，加之此时容积流量过小，汽流轴向分速度较低，使压力面回流区轴向影响范围稍有减小。

由图4可知，同一工况下不同叶高截面处的流动状态存在差异，压力面流动分离现象首先在动叶根部前缘点附近产生，且当k=0.290时回流区范围随叶高的增加而减小直至消失。为了进一步说明压力面发生流动分离时的动叶三维流场情况，引入图5所示的不同k值时动叶压力面和下端壁极限流线图。

a． k=0.290

b． k=0.330

图5a中k=0.290时的工况与文献[16]类似，此时在动叶压力面与下端壁附近均发生了流动分离。k=0.290时动叶压力面前缘点附近沿叶高方向形成一条分离线，靠近分离线的下游流体在40%左右轴向弦长内形成了大面积回流区且漩涡占据了整个叶高，导致近壁区域出现强烈的回流和径向流动。40%轴向弦长及其后区域径向流动逐步减弱，但整体流线呈斜下方趋势。此外，k=0.290时下端壁附近也出现了明显的流动分离，分离区内反向流体沿斜上方运动并向分离线靠拢。对比发现，k=0.330时压力面与下端壁附近均未出现回流，流动效果较好。综上所述，k=0.290为调节级动叶流域出现流动分离现象的起始点。

3.2 级后工质温度的分析

速度三角形法和比例系数法都是计算级后工

质参数的传统方法，由于笔者主要介绍数值模拟方法，因此只将新方法与传统方法所得结果进行比较。假设此时主汽阀和调节阀全开，则3种方法计算结果之间的相对误差如图6所示。

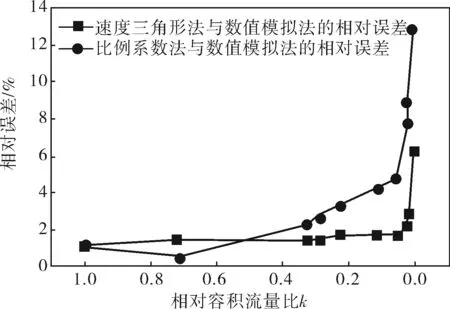
图6 不同级后工质温度计算方法间

由图6可知，在k>0.026范围内数值模拟法与速度三角形法计算结果的相对误差小于2%，且基本保持不变，这是因为调节级径高比较大，流场沿半径方向虽有变化但变化程度较小，平均直径处汽流参数仍适用于变工况的计算，虽然k≤0.290时动叶压力面附近已出现流动分离，但此时仍可用速度三角形法估算级后工质温度；当k≤0.026时，由于动叶出口吸力面附近出现了流动分离，使平均直径处汽流出汽角相比于设计工况发生了较大变化，导致两种方法计算结果的相对误差呈大幅上升趋势，此时速度三角形法得到的级后工质温度存在较大偏差，应采用数值模拟方法进行计算。比例系数法计算结果与数值模拟结果的相对误差在k=0.330时已大于2%，且随k值的减小而增大，在k<0.110范围内增幅更为明显，可见比例系数法所得结果在容积流量较小时并不理想。综上所述，为得到准确的调节级级后工质温度，当k>0.026时可采用速度三角形法进行计算，当k≤0.026时应采用数值模拟方法。

4 结论

4.1对动叶三维流场的分析表明，当k=0.290时，由于入口汽流负攻角较大，下端壁和压力面附近首次出现流动分离。当0.026

4.2对数值模拟结果与速度三角形法计算结果的分析表明，当k>0.026时，两者的相对误差小于2%，虽然在0.026

4.3对数值模拟结果与比例系数法计算结果的分析表明，当k≤0.330时，两者相对误差大于2%，可见容积流量较小时，采用比例系数法所得结果存在较大误差，相比之下，数值模拟结果准确度更高。

[1] 陈坚红,阮伟,任浩仁,等.冷态启动温升率对汽轮机转子寿命影响的研究[J].动力工程,1997,17(6):11～15.

[2] 袁鹏飞,盛德仁,陈坚红,等.汽轮机转子热疲劳寿命损耗监测面的有限元分析[J].电站系统工程,2004,20(2):43～44.

[3] 付忠广,杜志锋,王梦娇.660MW超超临界汽轮机转子热应力的研究[J].现代电力,2012,29(1):60～64.

[4] 袁利军.300MW机组中压缸启动热应力计算与启动优化[D].北京:华北电力大学,2005.

[5] 訾宏达,方韧,徐星仲,等.汽轮机部分进汽调节级三维流场的非定常数值模拟[J].动力工程,2007,27(5):721～724.

[6]Lampart P,Szymaniak M,Rzadkowski R.Unsteady Load of Partial Admission Control Stage Rotor of a Lager Power Steam Turbine[C].ASME Turbo Expo 2004:Power for Land,Sea and Air.Glasgow:American Society of Mechanical Engineers, 2004:237～246.

[7] Hills N J.Whole Turbine CFD Modelling[C].ASME Turbo Expo 2007:Power for Land,Sea and Air.Montreal:American Society of Mechanical Engineers,2007:817～824.

[8] 谢金伟,王新军,廖高良,等.汽轮机调节阀-调节级段三维流动与压力损失数值研究[J].中国电机工程学报,2014,34(20): 3376～3383.

[9] Hushmandi N B,Hu J,Fridh J,et al.Numerical Study of Unsteady Flow Phenomena in a Partial Admission Axial Steam Yurbine[C].ASME Turbo Expo 2008:Power for Land,Sea and Air.Berlin:American Society of Mechanical Engineers,2008: 713～722.

[10] He L.Computation of Unsteady Flow through Steam Turbine Blade Row at Partial Adimission[J].Proceeding of the Institution of Mechanical Engineers Part A:Journal of Power and Energy,1997,211(3):197～205.

[11] 阳虹,杨建道,李军,等.汽轮机调节级气动性能分析和结构优化设计[J].热力透平,2011,40(1):5～10.

[12] 李建兰,郭绪宏,余辰,等.汽轮机调节级汽流激振突变模型研究[J].中国电机工程学报,2013,33(11):39～46.

[13] 杨建道.空冷50MW机组低压缸变工况三维流场数值分析[J].热力透平,2007,36(1):53～56.

[14] Senoo S,Segawa K,Hamatake H,et al.Computation for Unsteady Compressible Flows in a Multi-Stage Steam Turbine with Steam Properties at Low Load Operations[J].Journal of Engineering for Gas Turbines and Power,2011,133(10): 711～722.

[15] 张仲彬,田艳静,曹丽华,等.小容积流量工况下汽轮机级内流场的数值分析[J].化工机械,2013,40(1):94～97.

[16] 朱光宇,俞茂铮,戴丽萍,等.汽轮机调节级动叶栅大负冲角工况下的三维分离流动研究[J].动力工程学报,2004,24(2): 189～194.

Studyof3DFlowFieldsinGoverningStageandSteamTemperatureafterStageofSteamTurbineatSmallVolumetricFlow

LI Yong, WANG Han-bei

(SchoolofEnergyandPowerEngineering,NortheastDianliUniversity,Jilin132012,China)

Taking the governing stage of a 300MW steam turbine as the object of study, the basic principle of proportional coefficient method and numerical simulation method was described; and the 3D flow fields in moving blades at governing stage with different volume flow ratios and at various working conditions were analyzed. Through comparing the steam temperature after governing stage and from the numerical simulation method with the results from the proportional coefficient method and velocity triangle method, the relative error between various calculation methods can be reached. These different calculation methods for steam temperature at different volumetric flows were discussed.

steam turbine, 3D flow field in moving blade, steam temperature after stage, relative volume flow ratio

*国家自然科学基金项目(51376041)。

**李 勇，男，1964年1月生，教授。吉林省吉林市，132012。

TQ053

A

0254-6094(2016)04-0489-06

2015-09-21)