管道缺陷漏磁检测单信道探头提离效应信号修复研究*

宋志强 张 莹 吴 江

(1.后勤工程学院；2.重庆海联职业技术学院)

管道缺陷漏磁检测单信道探头提离效应信号修复研究*

宋志强**1张 莹2吴 江1

(1.后勤工程学院；2.重庆海联职业技术学院)

漏磁检测方法是输油管道无损检测的重要方法，但检测探头提离效应是制约检测效果的重要原因，寻求一种合适有效的方法，对由于提离效应造成的信号畸变进行修复，提高缺陷漏磁检测结果准确度是工程应用研究的重要一环。最小二乘法能较好地实现对提离效应造成的信号畸变的修复，为消除提离效应造成的影响、提高检测的准确度提供了一种有效的方法。

输油管道 无损检测 漏磁检测 提离效应 信号修复 最小二乘法

漏磁检测方法广泛应用在输油管道检测、道路安全检测等工程检测领域。研究发现，在工程实际应用中，由于环境的影响和制约，检测探头提离值并不是分布在一个固定的区域，而是呈现不规律分布趋势，在工程应用过程中导致发生检测探头提离效应，从而造成检测信号的失真或畸变[1～4]。为保证提离值漏磁检测信号的完整性，以确保描述裂纹缺陷漏磁检测信号的正确性，必须对检测信号进行修正。

1 漏磁检测探头提离效应分析

在研究中发现，对于不同的检测探头提离值，随着提离值的变化，检测信号图谱分布在敏感区、线性区和盲区，不同区域有着不同的特性，在检测过程中，应确保检测探头提离值处于线性区域，以保证检测效果[4～6]。

利用漏磁检测实训平台[4]，利用MFL-4032A漏磁/磁记忆检测仪，通过建立提离效应实验平台[5]进行实验测定，检测缺陷试样Y1在不同提离值(0.5～10.0mm)时的漏磁检测信号,将不同提离值信号放置于同一图中，对信号数据进行数据图谱构建，如图1所示。对图1中检测数据进行区域划分：敏感区1～4mm、线性区为4～7mm、盲区和恒定区为8～10mm，其中提离值为0.5mm时，实验过程检测数据变化剧烈，故不做分析。每个传感器通道的基线都不在同一位置上。而对于检测缺陷的漏磁检测磁场梯度是磁场强度在空间中某一点变化量最大的方向与数值。对于常用的信号平均值法来消除提离效应的方法，由于信号处于非线性工作区域，而平均值消除提离效果是建立在线性拟合的基础上，在消除过程中，会间接产生新的更不易识别的噪声信号[7]，必须寻求更为有效的方法对信号进行修正。

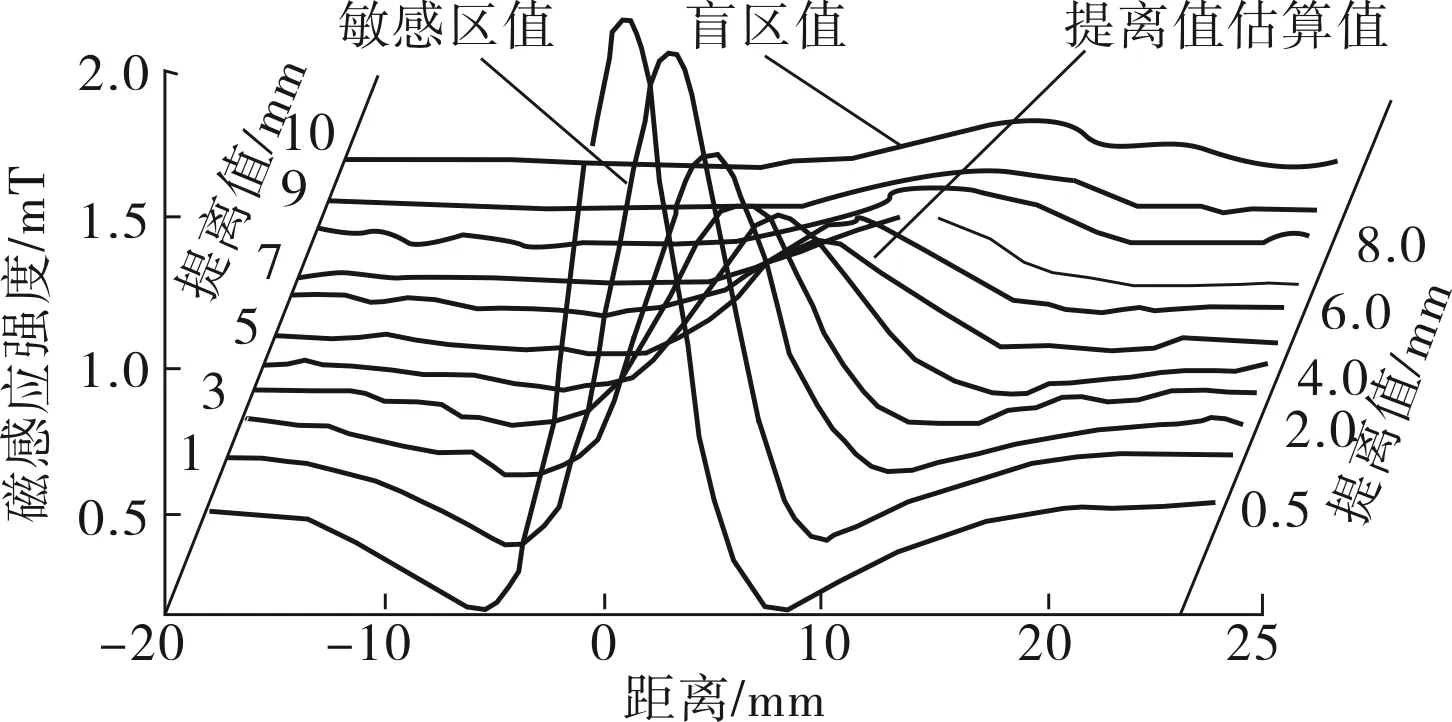
图1 不同提离值漏磁检测信号

2 基于最小二乘法的单信道探头提离效应信号修复

针对传感器探头提离效应的影响问题，一些学者对此进行了大量的研究[8～10]，对因提离效应产生的信号波动常用加权平均值的方法来进行消除[9]。加权平均值消除方法的根本思想是通过平均值将由提离效应带来的误差减小到最小，通过对各测量值的全局性差值运算以消除提离效应。加权平均值前提是提离因素的效应控制在线性变化区域，即控制在极小的固定区域内。

然而在研究中发现，如果仅以消除平均值的方法进行线性关系消除提离效应产生的影响，就会造成漏磁检测信号多余噪声的产生，影响到检测的准确性。要确保检测的准确性与精确度，就必须建立相应的补偿机制进行信号补偿与修正[9，10]。

由研究可知：提离值的大小与检测信号的峰峰值之间呈线性与非线性混合的模式，可以寻找相应算法对信号的提离效应影响进行补偿[5，10]。

设漏磁检测信号全集为X(t):Rd→Rd，消除提离效应后信号为S(t):Rd→Rd(未知)。当提离值为设定提离值时，局部信号为x0(t)，s0(t)为基函数。

对S(·)可以在任意t点取值，但是由于提离效应的存在，有部分信号误差。设xn(t)为第n个局部区域时检测的数据值集合，那么观察值为Yn+1=Sn(t)+εn+1。

εn为测量误差列，可以通过X(t)与H(t)之间的运算来求得，故求S(·)就可以转化为求解随机逼近(Robbins-Monro，RM)问题[11]。依据随机逼近算法[12]，取任意数列{φk}为增益系数，记为：

对s0(t)的第n+1次逼近为：sn+1(t)=sn+φnYn+1。

由RM算法将它转化求解增益系数[13]，即以随机逼近的方式求解，根据KW(Kiefer-Wolfowitz)算法[11]，可以利用它对X(t)数据的相互的差商运算来估计出S(t)的数值，从而求得消除提离效应后信号数据集S(t)，得到消除提离效应后的信号。

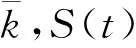
使用斜率法对漏磁检测信号值进行归一化处理，即：

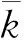
设采样后信号总长度为N，记m为小于或等于N/3的最大整数，对上式进行可离散化处理：

式中，Ts为采样周期；xi为x(t)经采样离散化后的数字信号。

假设在测量中不存在系统误差，同时，在平均斜率法进行校对过程中，已经对相应的部分系统误差进行了修正，则x(t)的观测值x(t)i围绕着期望值 摆动，其分布为正态分布。将利用平均斜率法得到离散信号值定为标准值[12]，利用最小二乘法进行二次计算[12]。

将信号s(t)作为观测量，而把所有的误差只认为是y(t)的误差。设s(t)和y(t)的函数关系为：

y(t)=f(s(t)；C)

C={c1,c2,…,cm}是m个待确定的参数。

则y(t)的观测值yi围绕着期望值摆动，其分布可视为正态分布，则yi的概率密度为：

其中σi是分布的标准误差，i=1，2，3，…，N。

观测值(y1,y2,y3,…,ym,cm)的似然函数：

取似然函数L最大来估计参数，应使：

根据上式要求，应有：

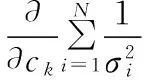
从而得到方程组：

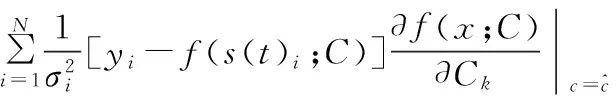
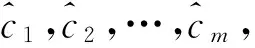
3 单信道提离效应信号数据修复实验验证

利用上述信号修复算法，选取缺陷试样Y2，在提离值实验平台[3，4]用漏磁检测仪器检测，在提离值为1～10mm时取得检测数据，经降噪校正处理后，得到信号图谱(图2)。

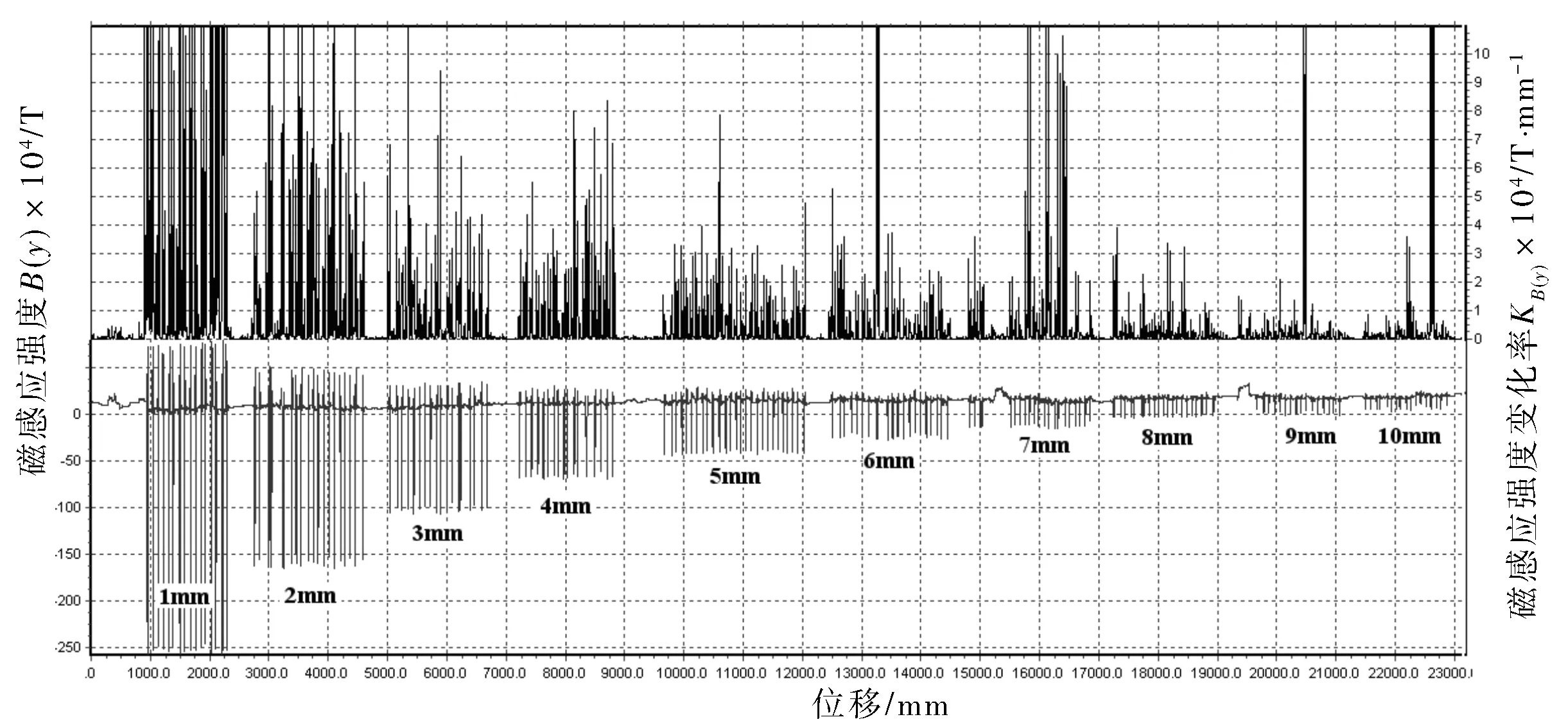
图2 提离值为1～10 mm时的检测信号

分别用平均值加权法与最小二乘法进行修复处理，为了更直观地分析结果，将各种情况的信号集中绘制在同一张图上，在1、10mm处信号的变化幅度剧烈，出现的信号误差太大，不做分析。图3显示了经过常用的平均值加权法消除提离效应后得到的试样Y2在不同的提离值下得到的信号图谱，图4是经过修正的最小二乘法消除提离效应后得到的修复波形。

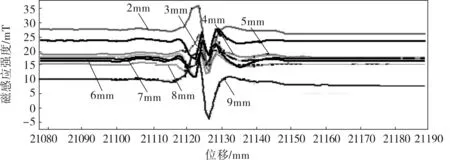
图3 平均值加权修复提离效应后信号图谱

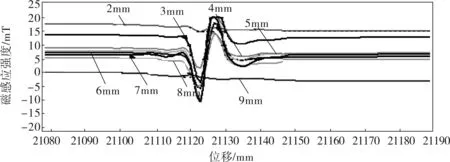
图4 最小二乘法修复提离效应后信号图谱

对图3、4的比较分析中可以看出：

a. 经过修正的最小二乘法在消除提离效应得到的修复信号方面要优于平均值加权法。

b. 平均值加权修复法在敏感区的消除效果不是很理想，存在较大的偏差，而最小二乘修复法效果要理想得多。

c. 在线性区消除效果上看，两种方法都取得了较理想的效果，这由线性区的特性决定。

d. 对盲区的检测信号修复，平均加权修复法效果保持了缺陷信号的特征，但是信号的幅度变化较大，在提离值为2、9mm处出现了较大的误差；而最小二乘修复法修正了信号的幅度，保证了缺陷信号特征的反映，但是在提离值为2、9mm处，出现了失效信号。

4 结束语

最小二乘法修复提离效应信号效果要优于平均值加权法，虽然利用最小二乘法修复时，出现了部分提离效应下信号的湮失，但却保证了总体效果的完整性，有利于对信号的分析，提高检测的精度和准确性。信号的湮失是由于在最小二乘法修复过程中，边缘提离值信号的丢失，造成在修复过程中部分信号数据丢失。因而可以通过加入相应的边缘提离值信号数据的方式进行修复，如在2mm提离值时，添加1mm提离值时的信号数据，即可实现信号的有效修复。

[1] Mandache C，Lefebvre J H V.Transient and Harmonic Eddy Currents：Lift-off Point of Intersection[J].NDT & E International，2006，39(1)：57～60.

[2] Kopp G，Willems H.Sizing Limits of Metal Loss Anomalies Using Tri-axial MFL Measurements：A Model Study[J]. NDT & E International，2013，55(4)：75～81.

[3] Mukherjee D，Saha S，Mukhopadhyay S.An Adaptive Channel Equalization Algorithm for MFL Signal[J].NDT & E International，2012，45(1)：111～119.

[4] 宋志强，李著信，张镇，等.碎片残余提离效应对在役油气管道漏磁检测影响分析研究[J].化工机械，2010，37(5)：539～543.

[5] 宋志强，李著信，张镇，等.检测探头提离效应对管道漏磁检测影响分析[J].后勤工程学院学报，2011，27(1)：29～34.

[6] 宋志强，李著信，张镇，等.基于连续小波变换的输油管道裂纹缺陷漏磁检测研究[J].化工自动化及仪表，2010，37(7)：35～39.

[7] Haueisen J，Unger R，Beuker T.Evaluation of Inverse Algorithms in the Analysis of Magnetic Flux Leakage Data[J].IEEE Transactions on Magnetics，2002，38(3)：1481～1488.

[8] 张玉华，孙慧贤，罗飞路，等.涡流探头提离效应的理论分析与实验研究[J].电机与控制学报，2009，13(2)：197～202.

[9] 王庆红，车威威，王子文.基于神经网络的数据融合算法在管道缺陷损伤识别上的应用[J].全面腐蚀控制，2013，(11)：70～74.

[10] 吴德会，柳振凉，张忠远，等.漏磁检测中提离值影响的三维有限元仿真分析[J].应用基础与工程科学学报，2013，21( 6)：1188～1198.

[11] 姚立东，赖圣，付跃文，等.飞机多层金属结构脉冲涡流检测提离效应的抑制[J].失效分析与预防，2013，8(3)：131～135.

[12] Plotnikov Y A，Bantz W J，Hansen J P.Enhanced Corrosion Detection in Airframe Structures Using Pulsed Eddy Current and Advanced Processing[J].Materials Evaluation，2007，65(4)：403～410.

[13] Tian G Y，Li Y，Mandache C.Study of Lift-off Invariance for Pulsed Eddy Current Signals[J].IEEE Transactions on Magnetics，2009，45(1)：184～191.

[14] Mirapeix J，Garcl'a-Allende P B，Cobo A，et al.Real-time Arc-welding Defect Detection and Classification with Principal Component Analysis and Artificial Neural Networks[J].NDT & E International，2007，40(4)：315～323.

[15] Li Y，Li Y F，Wang Q L，et al.Measurement and Defect Detection of the Weld Bead Based on Online Vision Inspection[J].IEEE Transactions on Instrumentation and Measurement，2010，59(7)：1841～1849.

ResearchonSignalsRepairofSingleChannelProbeLift-offEffectinPipelineMFLDetection

SONG Zhi-qiang1, ZHANG Ying2, WU Jiang1

(1.PLALogisticalEngineeringUniversity,Chongqing401131,China; 2.ChongqingHailianVocationalandTechnicalCollege,Chongqing401120,China)

MFL detection is an important method for nondestructive testing of pipelines, and detection probe’s lift-off restricts the detection effect. Finding a suitable and effective method to repair signal distortion which incurred by the detection probe’s lift-off and to improve leakage magnetic detection accuracy mean great to both engineering application and research. Making use of the least squares method can repair lift-off signals effectively and can eliminate the lift-off effect and improve the detection accuracy.

oil pipeline, NDT, MFL testing, lift-off effect, signal repair, least squares method

*重庆博士后基金项目(XM2014099)。

**宋志强，男，1978年7月生，副教授。重庆市，401311。

TQ055.8+1

A

0254-6094(2016)04-0457-05

2015-07-28，

2016-07-08)