《代微积拾级》的主要内容研究
张必胜
(遵义医学院 医学信息工程系,贵州 遵义 563000)
·科学技术史·
《代微积拾级》的主要内容研究
张必胜
(遵义医学院 医学信息工程系,贵州 遵义 563000)
基于李善兰和伟烈亚力合译著作《代微积拾级》原始文献内容的分析和讨论,为研究19世纪末西方数学传播史提供文献支持。译著的主要内容有解析几何、微分学和积分学。通过内史研究,结果得出解析几何、微分学和积分学是第一次系统地在我国传播,首次从内史角度对其中的解析几何、微分学和积分学进行比较分析。结论得出《代微积拾级》的翻译出版是在中国传统数学的影响下与对西方数学半符号化的接受的历史条件下的产物。《代微积拾级》首次引进了西方分析学的内容体系,并使中国传统数学的发展更具有科学性和系统性。
李善兰(1811—1882);伟烈亚力(Alexander Wylie,1815—1887);《代微积拾级》
1859年,李善兰(1811—1882)和伟烈亚力(Alexander Wylie,1815—1887)合译的著作《代微积拾级》(简称《拾级》)在上海墨海书馆刊行[1]。《拾级》翻译的底本是美国著名数学教育家、数学家罗密士(Elias Loomis,1811—1889)在1851至1852年出版的Elementsofanalyticalgeometryanddifferentialandintegralcalculus(《解析几何与微积分基础》,以下简称《基础》)。《基础》是由美国纽约的哈普兄弟出版公司(New York: Harper & Brothers Publishers)出版发行的,采用英文出版,而当时没有中文发行版[2-4]。李善兰和伟烈亚力合译时,从中英文的差异来看,二人都认为翻译的难度很大,而且其内容对当时国人来说也是首次接触,故而形象地取名为《代微积拾级》[5]。关于《拾级》的翻译出版情况已有论述[5]。
关于李善兰和伟烈亚力合译《拾级》的研究,有学者对其底本的版本进行了考究[6]。通对原始文献的对比研究认为其底本应为1852年版,而1851年版与1852年版在内容上没有实质性的不同。有从历史角度对这一历史事实进行了论述[7-8]。这些都是从历史文化方面来论述《拾级》翻译出版的这一事实。有对其内容中的一些具体问题进行论述[9],这些论述都是对《拾级》中某一题的分析和论述。有学者对其中相关例题和习题进行研究[10]以及对国外数学发展的影响[11],这是一种中外比较的研究。从翻译的符号系统和传统数学表达模式方面进行研究目前仅有一篇博士学位论文[10],本文则从其主要内容来分析和比较其与传统数学的关系,以及其中的数学思想,特别是李善兰通过自己对传统数学的掌握和对西方数学本质内容的理解以及传统数学符号化来审视李善兰对西方数学的接纳,通过内史分析来审视《拾级》对晚清数学科学性和系统性的影响。

图1 《基础》与《拾级》的封面Fig.1 Cover of Elements and Shi Ji
李善兰是我国著名的数学家,对我国晚清数学的西化和中国传统数学的西传做出了历史性的贡献。关于李善兰传播西方符号代数学已经有相关论述[12-13]。同时,关于李善兰传统数学方面的论述已有相关文章[14-17]。伟烈亚力是英国著名的汉学家,关于他向我国传播西方科学和西方科学史以及向西方传播我国传统科学和科学史的论述已经有相关文献。伟烈亚力和李善兰在翻译《拾级》的同时也翻译了我国第一本西方符号代数著作《代数学》,该著作为英国著名数学家和数学史家德·摩根(Augustus De Morgan,1806—1871)在1837年出版的Element of Algebra一书[12]。《拾级》共有18卷,其中第1~9卷是代数几何,主要介绍解析几何。第10~16卷是微分学,主要介绍微分理论。第17~18卷是积分学,主要介绍积分理论。即全书分为三大部分,第一部分代数几何,第二部分微分学,第三部分积分学。《拾级》有两个序言,其中一个是李善兰的自序,李善兰通过序言介绍了中国传统数学,特别是其中四元术与代数的异同,论述了微积分发展史,传统微积分思想及其微积分求解的方法,微积分的数学应用,最后对罗密士及其《基础》一书的结构给予了较高的评价。李善兰在序言中谈到“中法之四元即西法之代数也,诸元诸乘方互乘积,四元别以位次代数别以记号法,虽殊理无异也。康熙朝时,西国来本之、奈端二家又创立微分积分二术,其法亦借经于代数,而其理实发于古未有之奇秘。代数以甲乙丙丁诸元代已知数,以天地人物之诸元代未知数;微分积分以甲乙丙丁之诸元代常数,以天地人物代之诸元代变数。理之大要,凡线面体,均设为由小渐大一刹那中之,所增之积即微分也,其全积即乃积分也。故积分逐层分之为无数微分,乃合无数微分仍为积分也。”[1]李善兰对中外微积分思想做出了一个简洁明了的概括,从古典的微积分思想到莱布尼茨(Gottfried Wilhelm Leibniz, 1646—1716)和牛顿(Isaac Newton, 1642—1727),对传统微积分思想的最后目的作出了解释,并且还说明了其翻译《拾级》的结构与西方不一样的原因和具体做法,用传统的符号系统来表示微积分理论。给定了翻译全书的8个规定和说明,《拾级》的翻译遵循着8个规定和说明,这样读者就能理解《拾级》的相关理论[10]。另一个是伟烈亚力所作的序言,同样对微积分发展史做出了论述。并且对中国数学史也有所评价,伟烈亚力指出微积分学说是西方人发明的,但是他同时也指出微积分思想在中国古代数学著作中不乏出现,但是其不用代数式,其代数的书写模式繁杂,故没有形成系统的学说。并且列举了一些数学家及其著作中出现的微积分思想,这其中特别是李善兰的传统数学著作及其中的经典微积分思想[15]。
14世纪前,我国传统数学理论处于世界领先地位。然而,从此就开始落后于西方近代数学。特别是随着西方符号数学的进入,传统的中算理论开始渐渐地被理论化的符号数学代替[12]。这一时期也出现了一些数学家在坚持传统数学研究的同时也吸收了西方近代数学理论。在这样的情况下也得到了一些成果,有的是独立得到,有的是在西方数学的启发下得到的一些代表性成果[17]。
1 几何学
《拾级》中的几何学指的是代数几何即为解析几何。解析几何系指借助坐标系,用代数方法研究几何对象之间的关系和性质的一门几何学分支,亦叫作坐标几何。解析几何包括平面解析几何和立体解析几何两部分。平面解析几何通过平面直角坐标系,建立点与实数对之间的一一对应关系,即是一种函数关系,以及曲线与方程之间的一一对应关系,运用代数方法研究几何问题,或用几何方法研究代数问题。故李善兰和伟烈亚力翻译“analyticalgeometry”为“代数几何”而未翻译为解析几何。李善兰和伟烈亚力在《拾级》的序言中叙述了解析几何发展史,从阿基米德(Archimedes, 287B.C.—212B.C.)到笛卡尔(René Descartes, 1596—1650)创立解析几何。并且对解析几何的主要内容和研究的对象进行了介绍,对一些特别的曲线进行了说明。17世纪初,由于航海、军事、天文、力学、经济、生产的发展,在数学史上,随着初等几何和初等代数的迅速发展,促进了解析几何的建立,并被广泛应用于数学的各个分支。在解析几何创立以前,几何与代数是彼此独立的两个分支。解析几何的建立在数学史上是第一次真正实现了几何方法与代数方法的结合,使数与形统一起来科学方法,这是数学发展史上的一次重大突破,也是科学史上的一次创举。因为作为变量数学发展的第一个决定性步骤,解析几何的建立对于后来微积分的诞生有着不可估量的作用。我国传统数学中就有解析几何的思想,李善兰在其传统数学著作《火器真诀》中关于解决射程问题的理论就是利用解析几何的思想,即用代数方程解决几何问题。说明李善兰对解析几何的理解,以至于1866年出版了《圆锥曲线说》3卷,该著作是专门研究圆锥曲线的,是属于解析几何的内容范畴[10]。从后来的著作可以看出李善兰对解析几何理论的掌握情况,故李善兰在对《拾级》中解析几何内容的翻译时,运用了他自己对解析几何的理解和中国传统数学中的解析几何思想和西方系统化理论相结合的翻译模式。

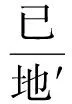
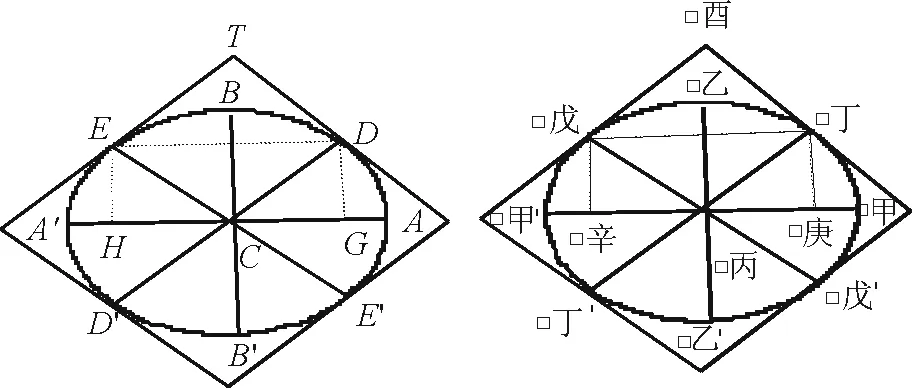
图2 椭圆Fig.2 Ellipse

表1 《拾级》中的代数几何目录
Tab.1 Contents of analytical geometry inShiJi

第一部分代数几何PartOneAnalyticalGeometry卷一以代数推几何Applicationofalgebratogeometry卷二作方程图法ConstructionofEquations卷三论点、论线、论纵横轴法Onthepointandstraightline卷四论圆OntheCircle卷五论抛物线OntheParabola卷六论椭圆OntheEllipse卷七论双曲线OntheHyperbola卷八诸曲线依代数式分类Classificationofalgebraiccurves卷九论越曲线、双曲螺线、对数曲线、摆线、螺线、亚奇默德螺线、对数螺线TranscendentalCurves
第8~9卷论述曲线分类和一些特殊的曲线。第8卷论诸曲线依代数式分类,共2款。表1所示,详细地讨论了二次曲线,首先将一般的二次方程通过旋转变换与坐标平移变换平方项的特殊形式,然后再对不同的曲线进行对应的分类。给出二次式的一般表达式,并且指出有圆、椭圆、抛物线和双曲线,▯甲地二┷▯乙天地┷▯丙天二┷▯戊天┷▯已=○,其类型由系数确定。还指出了三次曲线有四大类曲线,通过各类曲线相关历史研究和总结最后得出结论为80种。而对于四次曲线而言,比三次曲线更为复杂,四次曲线的一般式如图3所示,表示比较复杂。欧拉(Leonhard Euler, 1707—1783)分四次曲线146类,共有5 000多种。因随次数增加,曲线类型更加复杂,故五次及五次以上的则不知。

图3 四次曲线Fig.3 Quartic curve
通过《拾级》中几何学内容的分析和李善兰传统几何学理论可以得出《拾级》中的几何学更系统化和公理化,而传统数学中的几何学注重其应用性,强调数值解,故而没有系统化。难度上也没有《拾级》深,但是李善兰关于圆锥曲线理论比《拾级》更深入。总体来说,《拾级》中的几何学比传统数学中的几何学更全面和更系统化。
2 微分学
在微分学史上,很早就有人用极限的方法来定义微分。17世纪,人类对该理论的认识也有很大的突破。费马(Fermat,1601—1665)在一封给罗贝瓦尔(Roberval,1602—1675)的信中,提及计算函数的极大值和极小值的方法和步骤,而这实际上已相当于微分学中所用导数法,设函数导数为零的点,然后求出函数极点的方法。另外,巴罗(Isaac Barrow,1630—1677)亦已经懂得微分思想,通过“特征三角形”,即相当于以dx,dy,ds为边的三角形,求出切线的方程,这和微分学中利用导数来求切线的方法是一致的。由此可见,人类早在17世纪已经掌握了微分的思想。李善兰在其传统数学著作《方圆阐幽》中就有无限微分的思想[15]。
《拾级》中第10~16卷为微分学,为其第二部分。主要介绍微分学的基本概念和微分运算,主要内容涉及有常数、变数、函数、显函数、隐函数、增函数、减函数、极限、微分等相关概念,导数称之为微系数。主要内容如表2所示。给出导数定义,并给出一些函数的导数及其微分公式。同时,也给出了微分公式及其运算后,最后给出了微分的应用。
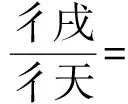
第13卷论初等超越函数和初等函数的微分,共10款。主要给出了指数函数、对数函数、正弦函数、余弦函数、正切函数、余切函数、复合函数和反三角函数等诸函数的微分公式,并且还给出了相关微分运算的结果,还给出了这些函数构成的复合函数微分的求法。

图4 泰勒级数Fig.4 Taylor series
Tab.2 Contents of differential calculus inShiJi

第二部分微分学PartTwoDifferentialCalculus卷十论函数微分DefinitionsandfirstprinciplesDifferentiationsofalgebraicfunctions卷十一叠微分SuccessivedifferentialsMaclaurin′stheoremTaylor′stheoremFunctionsofseveralindependentvariables卷十二第一次微系数解、论函数极大极小、求函数极大极小捷法SignificationofthefirstdifferentialcoefficientMaximaandMinimaoffunctions卷十三越函数、指函数微分、对函数微分、圆函数微分Transcendentalfunctions卷十四曲线义、用微分推曲线之四法、论极曲线之切线、次切线、论曲线及曲线之面积、论极曲线及其面积之微分、曲线之体积诸微分、论曲线之渐近线Applicationofthedifferentialcalculustothetheoryofcurves卷十五曲率半径、渐伸线诸例、渐伸线、摆线理RadiusofcurvatureEvolutesofcurves卷十六论一切曲线中诸理Analysisofcurvelines
第14~16卷主要论述微分应用问题。第14卷论述用微分推曲线四法、论极曲线的次切线、切线、论曲线及曲线的面积和曲线的体积诸微分、论极曲线及其面积之微分、论曲线的渐近线,及其在极坐标系下的应用,共13款。给出了相关的公式和在极坐标下的对应公式,主要内容如表3所示。包括了切线、法线、次切线、次法线、弧长微分、曲面、旋转曲面的面积微分、旋转体的体积微分、以及曲线的渐近线问题,如表3所示。第15卷讨论了曲率、曲率半径、渐曲线。共5款。第16卷论曲线的凹凸性和奇异点,共9款。首先给出了曲线上一点的切线与横轴平行或者垂直时曲线与函数微分之间的关系,其次讨论了函数图象的凹凸性与二阶微分之间的关系,最后讨论了曲线上各种点的性质,重点、拐点、孤立点和歧点与导数之间的关系。本卷主要是用导数的方法来研究函数图象特征[10]。通过导数这个工具可以解决很多实际问题,不管是在几何学上,还是在实际应用中的相关问题,都可以用导数来解决相关问题。这种系统化的成套理论对李善兰传统数学思想有着很大的影响,同时,李善兰采用了中西数学思想相互渗透的方法进行论述。
表3 公式对照表
Tab.3 Formula correspondence table

微分直角坐标系下微分公式极坐标系下微分公式切线地二┷彳地二地二彳天二y2+y2dx2dy2未二┷彳未未彳酉()二r2+rdtdr()2次切地彳地彳天ydxdy彳未未二彳酉r2dtdr法线地二┷彳天二地二彳地二y2+y2dy2dx2未二┷彳酉未彳未()二r2+rdrdt()2次法地彳天彳地ydydx彳酉未二彳未r2drdt弧长彳天二┷彳地二dx2+dy2彳天二┷未二彳酉二dr2+r2dt2曲面地彳天ydx二未二彳酉r22dt旋曲彳▯申=二周地彳天二┷彳地二 dS=2πydx2+dy2旋体彳▯亥=周地二彳天 dV=πy2dx
中国传统数学中很早就有无限分割的思想,从数学发展史来看,特别是中国传统数学有了微分学前两个阶段的出色工作,其中许多微分思想和微分公式都可以用来描述简单的微分。但是,由于数学符号表示系统上的八股取士和封建统治的文化专制,还有盲目排外等因素使其在微分学的最后关键一步落伍了。
3 积分学
积分概念是微积分学与数学分析里的一个核心概念。通常分为不定积分和定积分两种。从图形上直观地说,对于一个给定的正实值解析函数,在一个实数区间上的定积分可以理解为是在平面直角坐标上,由曲线、直线以及坐标轴所围成的曲边梯形的面积值。然而,积分的一个严格的数学定义由数学家黎曼(Riemann,1826—1866)给出。黎曼的定义运用了极限的概念,把曲边梯形设想为一系列矩形组合的极限。从19世纪起,更高级的积分定义逐渐出现,有了更多关于积分的定义,有对各种积分域上的各种类型的函数的积分[18]。比如,路径积分是多元函数的积分,积分的区间不再是一条线段,即不再是积分区间,而是一条平面上或空间中的曲线。在面积积分中,曲线被三维空间中的一个曲面代替。对微分形式的积分是微分几何中的基本概念等。李善兰的积分思想主要是在其传统数学著作《方圆阐幽》中,在这一著作里给出的“尖锥术”是李善兰创造的一种求解面积和体积的普遍算法,通过这一算法进而用来解决诸如对数计算和级数展开之类的数学问题。李
善兰称其为“尖锥求积术”简称为“尖锥术”,这实际上就是一种求和方法,一种无限积分的思想[15]。李善兰给出了一些简单函数的积分公式、一些函数的幂级数展开等结果,而这些理论是要通过系统的积分理论才能得到的结果和内容。

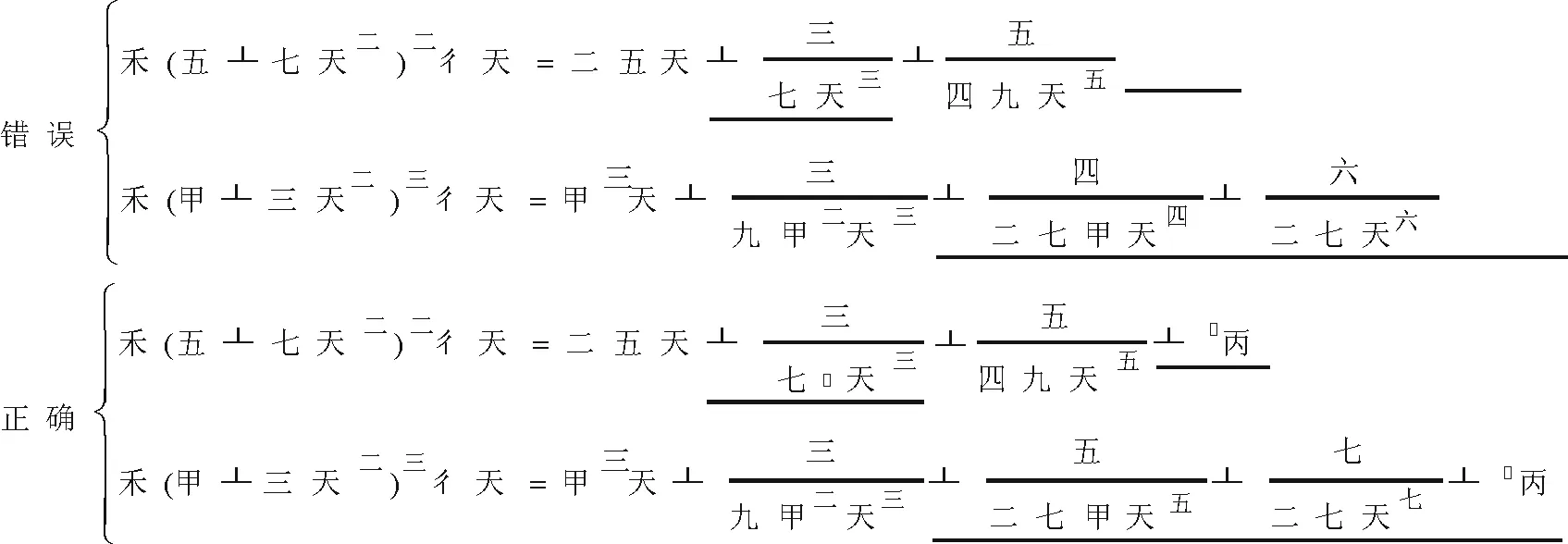
图5 错误比较Fig.5 Comparison error
第18卷主要讨论了求曲线长、面积和体积,旋转曲面的面积,旋转体的体积,本卷没有分款。《拾级》开篇论述到“用积分术令曲线改直线之理、求曲线面积、求曲面积、求曲线体积[1]”, 主要内容如表4所示。即主要是应用积分理论解决实际问题。其中主要解决曲线长,曲线构成的平面面积,曲面积及曲面旋转构成的旋转体体积等。本卷没有进行分款,一共有四个部分,分别给出了曲线长公式、曲面面积公式、旋转曲面公式、旋转体体积公式等。
表4 《拾级》中的积分学目录
Tab.4 Contents of integral calculus inShiJi

第三部分积分学PartThreeIntegralCalculus卷十七总论、论各微分之积分、论弧线微分之积分、用级数求积分法、论合名微分之积分IntegrationofmonomialdifferentialsOfbinomialdifferentialsOfthedifferentialsofcirculararcs卷十八用积分术令曲线改直线之理、求曲线面积、求曲面积、求曲线体积Applicationsoftheintegralcalculus

李善兰的传统积分思想主要体现在其著作《方圆阐幽》中,李善兰在其中给出了一种名为“尖锥术”的算法,这实际是李善兰创造的一种关于确定面积或体积的无限分割与极限求和的一般性算法,并且用该方法还可以解决诸如对数计算、近似值计算、级数求和、级数展开之类的重要问题。李善兰的极限思想表现在无限分割和求和的极限计算中,《方圆阐幽》中有“盈尺之书由迭纸而得,盈丈之绢由积丝而成”这一无限求和的积分思想。从这种无限分割和求和的思想来看,李善兰认为这些点、线、面、体是有实体的形状或客观存在,而且点、线、面、体诸多元素只是有其形状大小不同。李善兰极限思想就体现在“点者体之小儿微者也,而线者体之长而细者也,故面者体之阔而薄者也。”[15]从本质上看,李善兰根据这一无限分割求和思想从根本上揭示了点、长度、面积、体积之间的关系。李善兰认为前者是后者的单位微元,即最小元素,后者就是前者的无限求和[16]。点就是线的单位微元,线就是面积的单位微元,面积就是体积的单位微元。李善兰通过这种单位微元之间的关系和计算可以得出无限求和并取极限的表达式,李善兰得出了一个无穷级数展开式,即给出的关于π表示为无穷级数的关系式:
通过此方法,李善兰还得到了一些函数的幂级数展开式和一些积分表达式的展开式之间相互关系式:
李善兰的积分求和思想主要是体现在其给出的十个“当知”中,这十个“当知”实际上是给极限一个全面的定义。并且李善兰给出了公式:
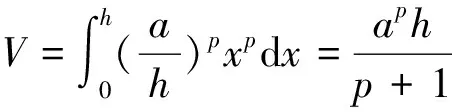

这实际上是垛积术理论中“拟p-1乘方垛”的体积应该为空间的p乘尖锥。采用了极限理论来求其积。李善兰在《对数探源》和《垛积比类》中给出了一些结论[17]。
李善兰传统数学理论中的积分思想以及独立给出的几个积分公式显然与《拾级》中的积分公式相同,而李善兰运用的是传统数学思想方法,得出的相关结论是李善兰的个人数学创造,而《拾级》则给出的是系统化的一套理论。李善兰在翻译《拾级》后,其对积分学的理解更加深刻,这一点可以从《拾级》翻译的历程和《拾级》翻译系统的数学语言符号系统中得以体现。
4 结 语
《拾级》的主要内容有解析几何、微分学和积分学3部分。内容上比较浅显,都是一些基本的定义和运算公式。但是《拾级》介绍的是一种变量数学和用解析的方法研究数学问题。在解析几何方面,《拾级》中代数几何部分介绍的都是解析几何基础方面的内容,其中特别是对几何作图和圆锥曲线的方程和图像方面作了深入地研究。解析几何是演绎数学的范畴,具有公理化的体系,是一门具有系统性的科学,这与中国传统数学中的算法有着很大的差别。中国古代传统数学是一种算法,是为了满足各种天文计算需要,例如历法的需要。其强调的只是一种结果,对这一系统和运算法则及其过程似乎不太重视。而解析几何的引进使得国人从分析的角度对几何有了新的认识。李善兰在笔译时,遇见一些公理,都会赞赏其美妙之处。这来自于他对中国传统数学的熟悉。解析几何的引进,也使得中算家对几何的研究有了更深的探索。在微分学方面,介绍了西方微分学发展的历史,介绍了微分的定义及其一些定理和微分的求法。同时,伟烈亚力也给西方学者介绍了中国传统数学中微分思想和方法,指出了中国传统数学中的微分思想与西方微分理论在思想的根源上是一致的,对中国传统数学中微积分思想给予了高度的评价。在积分学方面,伟烈亚力也给西方学者介绍了中国传统数学中积分思想和方法,指出了中国传统数学中的积分思想与西方积分理论在思想的根源上同样也是一致的,对中国传统数学中积分思想给予了高度的评价。《拾级》主要介绍的是不定积分的求法和牛顿-莱布尼茨公式。从《拾级》的内容上看,其理论深度不够,但是应该从历史的角度来评价《拾级》的意义。《拾级》是我国最早全面介绍西方分析数学的著作,虽然《拾级》的翻译出版离莱布尼茨和牛顿创立微积分理论已经过去近200年,但是这毕竟是中国第一次接触西方系统化的数学,是中国近现代数学的起步。《拾级》不仅对我国数学有着深远的影响,还对日本数学有着一定的影响。从历史的角度来看,《拾级》深深地影响着中国近现代数学的理论研究,并且还推动了近现代数学教育的发展。从后来中国传统数学家对《拾级》的研究和后续著作对《拾级》的解读可以看出《拾级》对中国传统数学西化的影响很大,从整个中国数学发展史的角度也可以看出中国数学现代化的历程。
[1] 罗密士.代微积拾级[M].伟烈亚力,李善兰,译.上海:墨海书馆,1859.
[2] LOOMIS E. Elements of Analytical Geometry and Differential and Integral Calculus[M]. New York: Harper & Brothers Publisher, 1851.
[3] LOOMIS E. Elements of Analytical Geometry and Differential and Integral Calculus[M]. New York: Harper & Brothers Publisher, 1852.
[4] LOOMIS E. Elements of the Differential and Integral Calculus[M]. New York: Harper & Brothers Publisher, 1874.
[5] 张奠宙.《代微积拾级》的原书和原作者[J].中国科技史料,1992,13(2):86-90.
[6] 高红成.《代微积拾级》的底本年代考辩[J].中国科技史杂志,2014,35(1):26-31.
[7] 梅荣照.中国第一本微积分学的译本——《代微积拾级》出版一百周年[J].科学史集刊,1960,3:60.
[8] 汪晓勤.微积分在中国的最初岁月——纪念《代微积拾级》出版140周年[J].文献,2000,22(4):219-229.[9] 汪晓勤.关于《代微积拾级》的一个注记[J].浙江大学学报(理学版),2001,28(4):384-393.
[10] 张必胜.《代数学》和《代微积拾级》研究[D].西安:西北大学,2013:1-250.
[11] 冯立升.《代微积拾级》在日本的流传和影响[J].自然辩证法通讯,1999,21(4):41-47.
[12] 张必胜.李善兰与伟烈亚力合译《代数学》的主要内容研究[J].西北大学学报(自然科学版),2013,43(6):1021-1026.
[13] 张必胜,姚远.《中西闻见录》与其数学传播[J].西北大学学报(自然科学版),2011,41(5):935-940.
[14] 张必胜.李善兰考数根法的研究[J].贵州大学学报(自然科学版),2011,28(2):1-5.
[15] 张必胜.李善兰微积分思想研究[J].贵州大学学报(自然科学版),2013,30(6):1-5.
[16] 张必胜,袁权龙.李善兰极限思想研究[J].贵州大学学报(自然科学版),2015,32(3):7-9.
[17] 张必胜.李善兰组合思想研究[J].贵州大学学报(自然科学版),2016,33(1):5-8.
[18] 李文林.关于牛顿制定微积分若干史实的注记[J].自然科学史研究,1989,8(2):138-146.
(编 辑 亢小玉)
Analysis on the main contents ofDaiWeiJiShiJi
ZHANG Bisheng
(Department of Medical Information Engineering, Zunyi Medical University, Zunyi 563000, China)
This research analyzes and discusses the main contents of the original document of theDaiWeiJiShiJitranslated by Li Shanlan and Alexander Wylie, which provides documentation for the spread of Western Mathematics of the 19thcentury. The book mainly contains analytic geometry, differential and integral calculus. Through its historical research, it finds that analytic geometry, differential and integral calculus spread in China and have analytic geometry, differential and integral calculus compared and analyzed from the perspective in the history for the first time. A conclusion that the translation and publication ofDaiWeiJiShiJiis a product of the lower half of Western mathematics symbolic acceptance of historical conditions under the influence of Chinese traditional mathematics.DaiWeiJiShiJiintroduced western analytics mathematics contents system for the first time, and made the traditional Chinese mathematics more scientific and systematic.
Li Shanlan(1811—1882);Alexander Wylie(1815—1887);DaiWeiJiShiJi
2016-03-15
国家社会科学基金资助项目(16XSS003)
张必胜,男,贵州思南人,遵义医学院副教授,博士,从事数学史研究。
O11
A
10.16152/j.cnki.xdxbzr.2016-06-023

