基于欧拉梁的准零刚度隔振系统动力特性分析
高 双 朱 翔 谌宗琦 李天匀
华中科技大学,武汉,430074
基于欧拉梁的准零刚度隔振系统动力特性分析
高 双 朱 翔 谌宗琦 李天匀
华中科技大学,武汉,430074
将两端受轴向压力的欧拉梁和线性弹簧并联,组成一个具备高静刚度和低动刚度的准零刚度隔振器。通过对隔振系统进行静力分析,给出系统具备准零刚度特性所需的条件。利用谐波平衡法求解系统的振动微分方程,分析系统的幅频特性,给出了系统的力传递率,讨论了阻尼、激励力等参数对系统传递率的影响。最后分析了该隔振系统的跳跃频率。研究结果表明:激励力以及初始偏移量的增大会使系统的隔振效果变差,因此要控制激励力的大小并尽量避免超载;阻尼比的选取需要综合考虑高频的隔振效果和有效隔振频率范围。
欧拉梁;准零刚度系统;谐波平衡法;力传递率;跳跃频率
0 引言
本文以两端受压的欧拉梁为负刚度机构,将它和线性弹簧并联,在一定条件下组成一个准零刚度隔振系统,对该系统进行了静力和动力特性分析,评价其隔振性能并分析系统参数对于隔振性能的影响。
1 准零刚度隔振系统的静力分析
准零刚度隔振系统由两端受压的欧拉梁和线性弹簧并联构成,两端受轴向压力的欧拉梁模型如图1所示,假设压杆长为l,弹性模量为E,惯性矩为I,垂向力为Fs,轴向压力为F。则该欧拉梁的弯曲微分方程为
(1)

图1 两端受压的欧拉梁模型
F→π2EI/l2时,梁中点挠度趋于无穷大,无法描述欧拉梁的后屈曲行为,因此将上述系统等效为由2根刚性杆和中间的扭转弹簧组成、具有几何非线性特点的系统[13],如图2所示。

图2 等效的非线性系统
对于梁的小变形,根据能量等效原则可以求得扭转弹簧的刚度ke=3EI/l。当梁的中点挠度为d时,系统的总位能为
(2)
由位能驻值原理可知∂V(d)/∂d=0,从而得到垂向力Fs的表达式,量纲一化后可以得到:
(3)
求导得到欧拉梁的垂向量纲一刚度:
(4)

图3 不同值时的不同特性
mg=kVd0
(5)

2 准零刚度隔振系统的动力特性分析
结合隔振系统的静力特性分析,建立系统动力分析模型,推导并分析准零刚度隔振系统的幅频特性、力传递率和跳跃频率特性,考虑不同参数对隔振性能的影响。
2.1 准零刚度隔振系统的幅频特性分析
根据式(3)可以得到系统的回复力(垂向力):
(6)
再根据式(5),可以得到梁中点挠度为x时整个隔振系统的回复力(垂向力):
(7)
考虑阻尼作用,引入线性阻尼(阻尼系数为c),若承载的物体受到简谐力FAcosωt的作用(FA为简谐力幅值),建立动力分析系统,则准零刚度隔振系统的受迫振动方程为
(8)
(9)
(10)
(11)
(12)
从式(12)可以看出:欧拉梁变形较小时,无论是否超载,欧拉梁与线性弹簧并联形成的准零刚度隔振系统都具备Duffing振子的特点,超载会使得系统回复力中二次项的系数不为零,即系统关于平衡点不具备对称形式。
(13)
利用谐波平衡法近似求解式(13),假设式(13)的解X(τ)=A0+A1cos (Ωτ+φ),即认为系统的稳态响应幅值为A1,同时还有一个附加的位移A0。将X(τ)的表达式代入式(13)并整理,得到[14]:
(14)
忽略式(14)中的二次谐波、三次谐波,由等式两边的谐波系数相等,可以得到:
(15)
整理式(15),得到关于A0的一元九次方程:
(16)
根据式(16)不难得到:
(17)
根据式(17)、式(15)的第三式可以得到关于A1的方程:
(18)
根据式(16)、式(18),作出A0-Ω和A1-Ω幅频响应图(图4、图5)。从图4a可以看出:系统的幅频曲线具有多值性,即一个激励力频率可能对应着多个稳态响应幅值A1,因此系统会出现频率跳跃现象;幅频曲线是向右弯曲的,并且γ越大,曲线弯曲程度越大,这说明系统的回复力具有渐硬特性;共振峰值随着量纲一激励力γ的增大而增大,对应共振频率也随之增大。从图4b可以看出:随着量纲一阻尼系数δ的增大,幅频曲线向右弯曲的程度变小,并且共振峰值和共振频率都随之减小,当δ增大到一定程度时,曲线不再具有多值性,此时系统不再会发生频率跳跃现象。


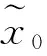



(c) γ=0.05,δ=0.1
分析该系统受迫振动的幅频曲线可以发现:在某些频率段,一个激励力频率对应多个振动的幅值,这种多值性会引起系统发生频率跳跃现象,如量纲一阻尼系数δ的变化会影响系统的共振峰值和共振频率,改变幅频曲线的弯曲程度,甚至使得多值性特点消失。
2.2 准零刚度隔振系统的力传递率分析
传递率是评价隔振系统的一个十分重要的指标,通常采用的传递率有力传递率和位移传递率,它们能很好地描述振动通过隔振器后减小的程度。力传递率Tf为
式中, Ft1、Ft2分别为弹性力和阻尼力的幅值;Fe为激励力。
本文需要分析的是准零刚度隔振系统的力传递率。
对于超载的准零刚度系统,式(12)的解可以由式(13)的解表示:
(19)

(20)
因为主要考虑的是动态力中的一次谐波分量,所以取弹性力的幅值[10]
将式(19)代入系统的阻尼力表达式,得到阻尼力幅值Ft2=δA1Ω,于是得到系统的力传递率:
(21)
(22)


图6 不同γ时系统的力传递率曲线

图7 不同δ时系统的力传递率曲线

图8 不同时系统的力传递率曲线(δ=0.1,γ=0.05)
从图6可以看出:保持其他参数不变,当量纲一激励力幅值γ增大时,系统的力传递率峰值也随之增大,并且对应的频率同时增大,在图中表现为峰值向右上方移动。另外,系统的跳跃频率也随γ的增大而增大。这说明激励力会影响系统的隔振性能,而且激励力增大会使得系统的隔振性能变差。
从图7可以看出:保持其他参数不变,当阻尼比δ增大时,系统的力传递率峰值会变小,对应的频率(下跳频率)也会减小,即峰值向左下方移动,阻尼比增大到一定程度如δ=0.3时,可能会使得曲线不具备多值性,频率跳跃现象消失。此外,应注意到阻尼的增大减小了力传递率峰值并拓宽了有效隔振的频率范围,但是这会使得系统在高频段的隔振效果变差,因此选取阻尼时,需要综合考虑高频的隔振效果和系统的有效隔振频率范围。
2.3 准零刚度隔振系统的跳跃频率分析
跳跃是非线性振动中很重要的一个特性,由2.2节分析可知,当系统的阻尼比增大到一定程度时,可能会使系统的跳频现象消失,激励力的大小也会影响系统的跳跃频率。因此需要分析该系统在未超载时的跳跃现象。根据式(15)很容易得到系统未超载时的幅频关系式:
(23)
从式(23)求解得到:
(24)
从式(24)可以看出,在一定范围内,有两支A1-Ω曲线,如图9所示。当激励力频率比Ω从点1开始减小到点2时,幅值A1沿着下方的曲线向左上移动;当Ω继续减小时,A1仍然沿着下方的曲线向左上移动直到点3;当频率再减小时,A1会从点3直接跳跃到点4,此时的Ω称为上跳频率,记为Ωu。随后A1会随着Ω的减小沿着上方曲线移动到点5。如果是从点5开始增大Ω,A1则是从点5经点4到点6,随后从点6向下跳跃到点2,随后从点2移动到点1。点6对应的频率称为下跳频率,记为Ωd。点3和点6之间的这一段曲线代表的是不稳的运动状态,通常是观察不到的。

图9 γ=0.1,δ=0.1时系统的幅频曲线
下面根据式(23)、式(24)来求解上跳频率Ωu和下跳频率Ωd。从图9易知,Ω的增大,A1由点6下跳至点2;Ω减小,A1由点1至点2,两曲线在Ωd相交,即下跳频率Ωd就是式(24)代表的两支曲线的交点:
(25)
式中,A1d为系统在下跳频率Ωd下的响应幅值A1。
从式(25)求得:
(26)
(27)


图10 Ωd-δ曲线

图11 Ωd-γ曲线
系统的上跳频率Ωu就是dΩ/dA1=0对应的频率。根据式(24)求解导数为零的条件:
(28)
式中,A1u为系统在上跳频率Ωu下的响应幅值A1。
显然式(28)中取负号才可能有解,由式(28)得到δ关于γ、A1u的解,代入到式(24)中取正号的表达式,化简可以得到:
(29)


图12 Ωu-δ曲线
图12中,实际有效的只是水平的那一部分(显然δ→0+时,Ωu→∞是不可能的)。从Ωu-δ曲线中有效的那一部分可以看出,当保持其他参数不变时,δ对Ωu的影响很微小,甚至可以忽略。所以可以令δ=0代入式(28)求得A1u,进而代入式(29)求得Ωu:
(30)
(31)
当上跳频率和下跳频率相等时,系统的跳跃现象消失,利用Ωd=Ωu可以得到此时的关系式:
(32)
根据式(32)作出Ωd=Ωu时的γ-δ曲线,如图13所示。

图13 跳跃现象刚好消失时的γ-δ曲线
由上文分析可知,γ很小时,系统的跳跃现象可能消失,再结合γ对Ωd和Ωu影响的分析,不难知道:在图13中的曲线上,对于某一给定的δ,对应的γ正好是系统的跳跃现象出现的临界值,曲线左上方的区域表示量纲一激励力γ超过了临界值,此时系统会出现跳跃现象;曲线右下方的区域表示量纲一激励力γ小于临界值,此时系统不会出现跳跃现象。如果要抑制跳跃现象,可以通过增大阻尼比δ来实现,而且阻尼比越大,γ允许变化的范围也越大。前文力传递率的分析指出,阻尼比的增大会降低隔振器高频范围的隔振性能,因此阻尼比δ并不是越大越好,仍然需要综合考虑多个方面的因素。
3 结论
(1)该隔振系统具有渐硬弹簧的特点,承载质量未超载时,可以看作是弹性力中一次项系数为零的Duffing振子;超载时,可以转化为受常力和简谐力共同作用的Duffing振子。此外,由于非线性的特点,系统会出现跳跃现象,但在一定条件下,跳跃现象会消失。
(2)该隔振系统的力传递率峰值和跳跃频率随量纲一激励力γ的增大而增大。激励力太大会使系统的隔振效果变差,因此要控制激励力的大小。
(3)阻尼比的增大可以有效降低系统的传递率峰值并拓宽有效隔振的频率范围,但会使高频段的隔振效果变差,因此阻尼系数的选取需要综合考虑高频的隔振效果和有效隔振频率范围。
(4)系统初始的偏移量是不利于隔振的,因此要尽量避免超载。
[1] Carrella A, Brennan M J, Waters T P, et al. Force and Displacement Transmissibility of a Nonlinear Isolator with High Static Low Dynamic Stiffness[J]. International Journal of Mechanical Sciences, 2012, 55(1): 22-29.
[2] Zhou J, Wang X, Xu D, et al. Nonlinear Dynamic Characteristics of a Quasi-zero Stiffness Vibration Isolator with Cam-roller-spring Mechanisms[J]. Journal of Sound and Vibration, 2015, 346(1):53-69.
[3] Xu D, Yu Q, Zhou J, et al. Theoretical and Experimental Analyses of a Nonlinear Magnetic Vibration Isolator with Quasi Zero Stiffness Characteristic[J]. Journal of Sound and Vibration, 2013, 332(14):3377-3389.
[4] Le T D, Ahn K K. A Vibration Isolation System in Low Frequency Excitation Region Using Negative Stiffness Structure for Vehicle Seat[J]. Journal of Sound and Vibration, 2011, 330(26):6311-6335.
[5] 白晓辉, 白鸿柏, 郝慧荣, 等. 正负刚度并联机构动力学分析及隔振仿真[J]. 机械工程师, 2009(11):87-89. Bai Xiaohui,Bai Honkbai, Hao Huirong, et al. The Dynamic Analysis and Simulation of Positive and Negative Stiffness in Parallel[J]. Mechanical Engineer, 2009(11):87-89.
[6] 彭献, 张施详. 一种准零刚度被动隔振系统的非线性共振响应分析[J]. 湖南大学学报(自然科学版), 2011, 38(8):34-39. Peng Xian, Zhang Shixiang. Nonlinear Resonance Response Analysis of a Kind of Passive Isolation System with Quasi-zero Stiffness[J]. Journal of Hunan University(Natural Sciences), 2011, 38(8):34-39.
[7] 徐道临, 余奇平, 周加喜, 等. 准零刚度隔振系统跳跃频率区间隔振研究[J]. 中国机械工程, 2014, 25(2): 230-235. Xu Daolin, Yu Qiping, Zhou Jiaxi, et al. Study on Vibration Attenuation in Jumping Frequency Interval of Quasi-zero Stiffness Vibration Isolator[J]. China Mechanical Engineering,2014, 25(2):230-235.
[8] Lan C, Yang S, Wu Y. Design and Experiment of a Compact Quasi-zero-stiffness Isolator Capable of a Wide Range of Loads[J]. Journal of Sound and Vibration, 2014, 333(20):4843-4858.
[9] Liu X, Huang X, Hua H. On the Characteristics of a Quasi-zero Stiffness Isolator Using Euler Buckled Beam as Negative Stiffness Corrector[J]. Journal of Sound and Vibration, 2013, 332(14):3359-3376.
[10] 刘兴天, 黄修长, 张志谊, 等. 激励幅值及载荷对准零刚度隔振器特性的影响[J]. 机械工程学报, 2013, 49(6):89-94. Liu Xingtian, Huang Xiuhang, Zhang Zhiyi, et al. Influence of Excitation Amplitude and Load on the Characteristics of Quasi-zero Stiffness Isolator[J]. Journal of Mechanical Engineering, 2013,49(6):89-94.
[11] 刘兴天, 孙靖雅, 肖锋, 等. 准零刚度微振动隔振器的原理和性能研究[J]. 振动与冲击, 2013, 32(21):69-73. Liu Xingtian,Sun Jingya, Xiao Feng, et al. Principle and Performance of a Quasi-zero Stiffness Isolator for Micro-vibration Isolation[J]. Journal of Vibration and Shock, 2013, 32(21):69-73.
[12] Huang X, Liu X, Sun J, et al. Vibration Isolation Characteristics of a Nonlinear Isolator Using Euler Buckled Beam as Negative Stiffness Corrector: A Theoretical and Experimental Study[J]. Journal of Sound and Vibration, 2014, 333(4):1132-1148.
[13] 徐博侯, 曲绍兴. 非线性力学导论[M].杭州: 浙江大学出版社, 2012.
[14] 高雪,陈前,滕汉东.液固混合介质隔振系统的主共振分析[J]. 机械工程学报, 2012, 48(15):90-95. Gao Xue, Chen Qian, Teng Handong. Primary Resonance Analysis of Solid and Liquid Mixture Vibration Isolation System [J]. Journal of Mechanical Engineering, 2012,48(15):90-95.
(编辑 张 洋)
Analyses on Dynamics Characteristics of a Quasi-zero-stiffness Vibration Isolation System Based on Euler Beam
Gao Shuang Zhu Xiang Shen Zongqi Li Tianyun
Huazhong University of Science and Technology,Wuhan,430074
Combining the Euler beam under axial pressures with a positive stiffness spring, a quasi-zero-stiffness vibration isolation system was obtained, which had high static stiffness and low dynamic stiffness characteristics. The requirements of the quasi-zero-stiffness system were achieved through the static characteristic analyses. The harmonic balance method was used to solve the dynamic differential equations. The steady state and amplitude frequency response of the system were also analysed. The influences of parameters such as damping and exciting forces on the force transmissibility of the system were discussed. At last, the jumping frequencies of the system were analysed. The results show that the increase of the exciting force and the initial offset make the effects of vibration isolation of system worse, therefore the amplitude of the exciting force should be controlled, and the overload should be avoided. To choose the proper damping ratio, the vibration isolation effect at high frequencies and the effective isolation frequency range should be considered comprehensively.
Euler beam; quasi-zero-stiffness system; harmonic balance method; force transmissibility; jumping frequency
2015-09-10
国家自然科学基金资助项目(51479079)
O328
10.3969/j.issn.1004-132X.2016.21.006
高 双,男,1990年生。华中科技大学船舶与海洋工程学院硕士研究生。主要研究方向为结构振动与噪声控制。发表论文2篇。朱 翔,男,1980年生。华中科技大学船舶与海洋工程学院副教授。谌宗琦,男,1989年生。华中科技大学船舶与海洋工程学院硕士研究生。李天匀,男,1969年生。华中科技大学船舶与海洋工程学院教授、博士研究生导师。

