整式加减“警示牌”

□王西峰

整式加减“警示牌”

□王西峰

在整式加减的运算中，一些同学对整式加减的概念不理解，运算法则掌握不熟练，计算过于马虎，因而会出现一些错误.现归纳几例，供大家反思.

误区一、概念错误

例1试判断下列各组单项式是否是同类项：①3x3y2与－5x2y3；②4ab2与－2xy2；③3x3y2与－y2x3.

错解：由同类项的概念可知，①、②、③都是同类项.

剖析：由于同类项必须同时满足两个条件：（1）所含字母相同；（2相同字母的指数分别相同，二者缺一不可.同类项与系数大小、字母的排列顺序无关.①中，3x3y2与－5x2y3字母相同但相同字母的指数不同，故不是同类项；②中，4ab2与－2xy2由于字母不同，故也不是同类项；③中，3x3y2与－y2x3字母相同且相同字母的指数分别相同，故是同类项.

正解：因为③中3x3y2与－y2x所含字母相同，而且相同字母的指数又分别相同，所以只有③是同类项.

误区二、括号前是负号时只改变首项符号

例2计算：2a－（5a－3b）＋（7a－b）.

错解：2a－（5a－3b）＋（7a－b）

＝2a－5a－3b＋7a－b

＝4a－4b.

剖析：错解的原因是括号前是负号时，去括号只改变了首项的符号.去括号的法则：当括号前是负号时，把括号和括号前面的负号一同去掉，括号里的各项都改变符号.

正解：2a－（5a－3b）＋（7a－b）

＝2a－5a＋3b＋7a－b

＝4a＋2b.

误区三、多项式相减，没有用括号括起来

例3 已知A＝x3－3x2－1，B＝2x2＋5，求：（1）A－B；（2）2A＋B.

错解：（1）A－B

＝x3－3x2－1－2x2＋5

＝x3－5x2＋4；

（2）2A＋B

＝2x3－3x2－1＋2x2＋5

＝2x3－x2＋4.

剖析：在本题中A与B表示的是两个代数式，每个代数式是一个整体，式子A－B表示的是两个代数式的差，代入时要先用括号括起来，故A－B＝（x3－3x2－1）－（2x2＋5）.同样（2）式中2A表示2与A的乘积，即2A＝2（x3－3x2－1），因此要用2去乘以A中的每一项.在实际应用中，常常先把一个整体用括号括起来再运算，以保证解题正确.

正解：（1）A－B

＝（x3－3x2－1）－（2x2＋5）

＝x3－3x2－1－2x2－5

＝x3－5x2－6；

（2）2A＋B

＝2（x3－3x2－1）＋（2x2＋5）

＝2x3－6x2－2＋2x2＋5

＝2x3－4x2＋3.

误区四、忽略分数线的作用

例4计算：3a2b＋（2ab2－a2b）－

错解：3a2b＋（2ab2－a2b）－

＝3a2b＋2ab2－a2b－a2b－

＝a2b＋

剖析：分数线不但具有除号的作用，而且还有括号的作用，所以如果分数的分子是一个多项式，在进行化简时，应注意分子是一个整体，运算时要用括号括起来，本题的错误正是忽略了分数线的括号作用.

正解：3a2b＋（2ab2－a2b）－

＝3a2b＋2ab2－a2b－（2a2b－ 3ab2）

＝3a2b＋2ab2－a2b－a2b＋

＝a2b＋

误区五、忽视多项式中不含项的意义

例5 当k取（）时，多项式2x2－3kxy－3y2＋xy－8中不含xy项.

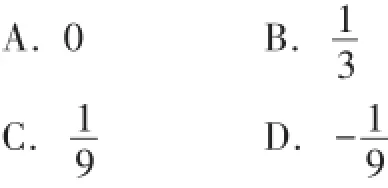
错解：因为多项式2x2－3kxy－ 3y2＋xy－8中不含xy项，所以－3k＝0，即k＝0.故应选A.

剖析：求解一个与多项式有关的问题，首先要对同类项作出正确的判断，然后进行合并.本题中－3kxy与xy为同类项，应先合并，合并后不含xy项，即xy项的系数为0，从而正确求解.

正解：因为2x2－3kxy－3y2＋8＝2x2＋（－3k＋）xy－3y2－8，

而多项式不含xy项，

误区六、合并不是同类项的项

例6 计算：2a2b－3a2b＋

错解：2a2b－3a2b＋

剖析：错解的原因是将不是同类项的项也随意地合并.判断同类项必须抓住两个条件：一是字母相同；二是相同字母的指数也相同，两者缺一不可.

正解：2a2b－3a2b＋

＝（2－3）a2b＋

＝－a2b＋

误区七、把字母和字母的指数相加减

例7 计算：3x2＋2x2＋5x2y－2x2y

错解：3x2＋2x2＋5x2y－2x2y

＝（3x2＋2x2）＋（5x2y－2x2y）

＝5x4＋3.

剖析：错解的原因是违背了合并同类项的法则，把字母和字母的指数也进行了加减.合并同类项的法则有两层意思：一是把同类项的系数相加，所得结果作为系数；二是字母和字母的指数不变.

正解：3x2＋2x2＋5x2y－2x2y

＝（3x2＋2x2）＋（5x2y－2x2y）

＝5x2＋3x2y.