考虑风速和导线高度影响的高压直流输电线下离子流场计算
许松枝,汪 沨,李 敏,邓 晓,2,谢望君,陈晓林
(1.湖南大学电气与信息工程学院,长沙 410082;2.近地空间电磁环境监测与建模实验室(长沙理工大学),长沙 410114)
考虑风速和导线高度影响的高压直流输电线下离子流场计算
许松枝1,汪 沨1,李 敏1,邓 晓1,2,谢望君1,陈晓林1
(1.湖南大学电气与信息工程学院,长沙 410082;2.近地空间电磁环境监测与建模实验室(长沙理工大学),长沙 410114)
为了预测高压直流输电线下的电磁环境,对不同条件下的地面离子流场分布进行了计算研究。采用Kaptzov假设,通过模拟电荷法计算人工边界处的标称电位,再结合泊松方程计算出空间电荷产生的电场,同时提出一种新的空间电荷密度更新公式,基于上流有限元方法求解离子电流密度方程。通过同轴圆柱电极电场问题验证了该算法的有效性,并利用考虑风速的单极高压直流输电线路模型说明了该算法的可靠性。最后,将其应用到不同导线对地高度和不同风速影响下的双极高压直流导线离子流场问题,结果表明导线对地高度和风速都会影响地面最大合成场强和离子流密度,且风速会使其发生偏移。
高压直流;离子流场;导线高度;风速;上流有限元法
随着电压等级的提高、输电容量的增加,高压直流输电线路给周边环境带来了诸多问题,如电磁场效应、无线电干扰、可听噪声等环境问题。这些问题一直是高压直流HVDC(high voltage direct current)输电线路设计[1]、运行和管理中必须着重考虑的。离子流场的计算分析对于HVDC输电线路前期的电磁环境评估和运行预测均具有重要的指导意义。
国内外学者对HVDC输电线路的离子流场计算问题进行一系列研究分析。Sarma等人[2]最早提出采用解析法来计算直流输电线下的离子流场,但该方法实际采用Deutsch假设,忽略了空间电荷对电场方向的影响,引入了一定的误差。美国电力科学院通过大量模拟实验,总结了离子流场与线路基本参数的关系,拟合出了反应合成场强和离子流密度的半经验公式[3],计算过程简单,但只适用于一些特定的输电线路。对离子流场的研究采用最多的是有限元类方法[4-7],该方法不再依靠Deutsch假设,而是采用更接近实际的Kaptzov假设[8],即导线表面起晕后,导线表面场强保持起晕值不变。日本学者Takuma等人[9-10]提出的上流有限元法,解决了离子流场计算中出现的数值不稳定问题。国内学者卢铁兵等人[11]将上流有限元应用到考虑风速存在时的离子流场计算当中,但只研究了对单极HVDC导线离子流场的影响。甄永赞等人[12]将边界电场约束方程法引入到了上流有限元法中,可以更准确地计算导体表面电荷密度和空间电荷产生的电场。罗兆楠等人[4,13]研究了直流输电线路有限元解法及三维合成场强的快速有限元计算方法,并将其应用于考虑临近建筑物下的离子流场问题。周象贤等人[14]基于有限体积与有限元法研究了直流输电线路合成场强的计算,并对地面合成场强进行了预测计算。
本文采用上流有限元方法对离子流场进行求解,基于Kaptzov假设,利用模拟电荷法计算人工边界处的标称电位,提出一种新的空间电荷密度更新公式,每次更新值都与导体表面节点场强值相关。通过计算具有解析解的同轴圆柱电极离子流场和单极HVDC导线离子流场问题验证了改进算法的可靠性和有效性。最后将改进算法应用到考虑水平风速和不同导线对地高度下的±800 kV特高压直流输电线路离子流场问题中。
1 离子流场的数学模型
1.1 模型基本假设
实际HVDC输电线路产生电晕的物理机理是非常复杂的,但进行空间离子流场计算时可以采取一定的假设以简化求解,具体如下:
(1)忽略电晕导体周围电离层的厚度;
(2)不考虑空间电荷的扩散,且离子迁移率与电场无关,视为常数;
(3)考虑风速影响时,风速恒定且方向不发生变化;
(4)导线表面起晕后,导线表面场强保持起晕场强不变,即Kaptzov假设。各类离子流的计算方法通常采用类似于预估-校正的方法寻找合适的空间电荷分布,以便使得此时的导线表面电场满足Kaptzov条件[15]。导线表面的电晕起始场强E0采用Peek公式计算[16],即

式中:r为导线半径;m为导线表面的粗糙系数;δ为空气相对密度。
1.2 离子流场的基本方程及边界条件
根据上述假设,对于双极直流线路的离子流场问题在考虑风速的影响下,可以得到直流离子流场问题的基本方程[9,15]为

式中:v+=K+E+w表示正离子的迁移速度;v-=-K-E+w表示负离子的迁移速度;w为水平方向恒定风速;E为空间合成场强;J+为正离子流密度;J-为负离子流密度;ρ+、ρ-为正负空间电荷密度;K+、K-为正负离子迁移率;R为离子的复合系数;ε0为真空介电常数;e为基本电子电量。
将式(4)和式(5)分别代入式(6)和式(7),并结合式(2)和式(3)可以得到

对上述方程的求解需要一定的边界条件,有限元方法的计算需要将输电线路电场的无限区域转化成有限区域考虑。将离导线较远处划出一条人工边界,这样导线表面和地面所围成的封闭平面区域便为计算区域。人工边界半径取为4倍导线高度最合适[17]。在导线表面附近,场强和空间电荷密度梯度很大,所以此部分采用加密三角元剖分,而边界区域电场和电荷密度变化较小采用稀疏三角元剖分,这样可以有效地控制剖分产生的节点和有限元计算形成的刚度矩阵阶数,进而可以有效地减少程序的计算量。HVDC整个区域采用不均匀三角元剖分的结果如图1所示。所需满足的边界条件如下:
(1)导线表面有φ=U,其中U为导线运行电压;
(2)地面满足φ=0;
(3)人工边界上满足φ=Uno,其中Uno为标称电位;
(4)导线表面保持起晕场强E0不变,即

图1 计算区域有限元剖分(6 576个三角元)Fig.1 Computational region with finite element mesh(6 576 triangular elements)
1.3 基于上流有限元法的离子流场计算
计算空间合成场强和更新空间电荷密度时,导线表面场强是否满足Kaptzov假设是确定计算过程是否完成的依据,因此导线表面场强的精确计算非常重要。假设导体表面电荷密度初始值为 ρ0,其表达式[17]为

式中:Eg为导线投影下方的标称场强;U0为导线的起晕电压;H为导线的距地高度。
利用模拟电荷法计算出人工边界的标称电位,再结合有限元方法,采用线性单元离散,求解泊松方程可以得到空间各点电位的数值解,再由式(3)计算出空间合成场强,最后根据求得的电位和场强来求解离子电流密度方程。其中求解空间各点的电荷密度是整个仿真程序中至关重要的一步,如果方法不适当将会导致结果不收敛。为了解决这个问题,本文采用上流有限元法对电流连续性方程进行求解。
这里需要寻找和判断上流单元,如图2所示。如果根据已知电荷密度的节点j和节点m来求节点i的电荷密度,就必须判断与节点i相关的三角形ijm是否构成上流单元(按逆时针方向)。若节点i的空间电荷密度迁移速度v与ji和mi的夹角都小于90°,则该三角形为上流单元。用数学表达式表示为

式中 :bj=ym-yi;bm=yi-yj;cj=xi-xm;cm=xj-xi;vx为x方向的迁移速度;vy为y方向的迁移速度。通过上流有限元计算得到的结果满足0<ρi≤max(ρj,ρm),即速度下方的节点电荷密度总是小于速度上方的节点,保证解的收敛性,也符合实际情况。

图2 节点i的上流单元判断Fig.2 Wind element judgment at node i
由于给定的电荷密度初值并不是实际值,故需要对导体表面电荷密度进行修正,本文经过多次计算分析提出一种导体表面电荷密度修正公式为


图3为本文的空间电荷密度更新公式与文献[15]的迭代误差对比图。
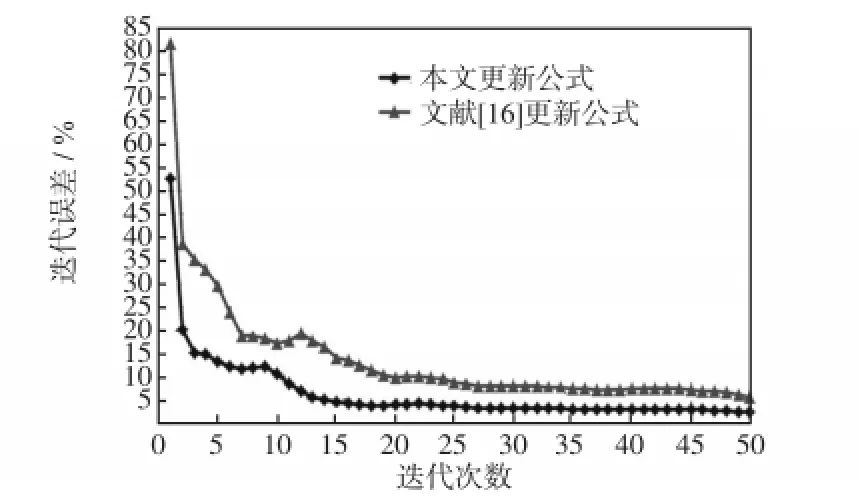
图3 空间电荷密度迭代误差与迭代次数的关系Fig.3 Relationship between iterative error of space charge density and the times of iterations
2 同轴圆柱电极离子流场计算
同轴圆柱离子流场是唯一具有解析解的离子流场计算模型,由Townsend首次给出了解析式[18],可以准确地验证改进算法是否正确。同轴圆柱离子流场的表达式如下:

式中d为空间一点到圆心的距离。
本文使用MATLAB编制了离子流场计算程序,并将计算结果与解析结果进行比较。图4为采用改进算法计算的场强、空间电荷密度和电位数值解与解析解的对比。从图4中可以看出数值解和解析解基本一致,从而验证了该方法的有效性。

图4 解析解与数值解的对比Fig.4 Comparison between numerical and analytical solutions
同轴圆柱电极结构如图5所示,采用文献[18]中的参数设置。

图5 同轴圆柱电极结构Fig.5 Structure of coaxial cylindrical electrode
3 单极HVDC导线离子流场计算分析

图6 不同风速下的离子流密度Fig.6 Ground level profile of ion current density at different wind speeds
本文采用文献[19-20]中的实验数据进行计算分析,实验模型参数为导线半径为0.25 cm,距地高度为2 m,K+为1.4×10-4m2/(V·s),起始电晕场强为45.05 kV/cm,起始电晕电压82.9 kV,分别计算了有风和无风两种情况下的离子流场。风速为w=8 m/s,方向为水平向右,对导线施加200 kV电压进行仿真,得到了不同风速下的地面离子流密度(如图6所示)和地面合成场强分布(如图7所示),以及考虑风速下的二维空间电位分布(如图8所示)和电荷密度分布(如图9所示)。从计算结果可见,本文的算法很好地解决了单极HVDV输电线路离子流场计算问题。地面合成场强和电流密度的计算结果与文献[18]的实验数据非常接近,导线投影下方的计算值与文献数据基本吻合。考虑风速时地面合成场强和电流密度的计算值与文献数据的最大误差分别为5.88%和6.38%。

图7 不同风速下的地面合成场强Fig.7 Ground level profile of electrical field strength at different wind speeds

图8 w=8 m/s时的空间电位分布Fig.8 Potential distribution in space with w=8 m/s

图9 w=8 m/s时的空间电荷密度分布Fig.9 Charge density distribution in space with w=8 m/s
4 双极HVDC导线离子流场计算分析
本文选用向家坝-上海±800 kV特高压直流输电线路为例进行计算[21],该输电线路参数为6xLGJ-720/50,子导线半径为1.72 cm,分裂间距为45 cm,线路极间距为22 m,导线距地高度21 m。正离子迁移率为1.4×10-4m2/(V·s),负离子迁移率为1.7×10-4m2/(V·s),离子复合系数取为2.0×10-12m2/s[9]。通常为了减少计算量,可采用电晕程度等效法将分裂导线等效为单根导线[14,19],同时基于不均匀三角元剖分计算区域(如图10所示),再结合改进算法计算地面离子流场。

图10 计算区域有限元剖分(25 656个三角元)Fig.10 Computational region with finite element mesh(25 656 triangular elements)
4.1 导线高度对离子流场的影响
在其他条件不变的情况下,计算不同导线距地高度对地面合成场强和地面离子流密度的影响如图11和图12所示。由图11可知,随着距地高度的增加,导线在地面产生的最大合成场强有明显减小的趋势。当对地高度分别为17 m、19 m、21 m时地面合成场强最大值分别为31.08 kV/m、26.70 kV/m、22.92 kV/m。当高度为17 m时,地面最大合成场强超过我国规定的±800 kV直流输电线路的限值30 kV/m,经计算导线最小距地高度不低于18 m。由图12可知,导线距地高度为17 m时,地面最大离子流密度为105.32 nA/m2;导线距地高度为19 m时,地面最大离子流密度为71.76 nA/m2;导线距地高度为21 m时,地面最大离子流密度为48.3 nA/m2。导线距地高度升高时,离子流密度逐渐减小,每升高1 m,大约下降11.37 nA/m2。由此得出提高直流架空线路高度可以有效地减小地面合成场强和离子流密度。线路架设高度每提高1 m就会使工程总造价提升很多,因此对导线架设高度的选择也是比较重要的方面。

图11 导线高度对地面合成场强的影响Fig.11 Influence of wire height on ground level profile of electrical field strength

图12 导线高度对地面离子流密度的影响Fig.12 Influence of wire height on ground level profile of ion current density
4.2 风速对离子流场的影响
导线对地高度取21m,其他导线参数不变,计算不同水平风速影响下地面合成场强和离子流密度,结果如图13和图14所示。从图13、14中结果可以发现水平风速从0 m/s逐渐增大到8 m/s时,地面合成场强和离子流密度的波峰值都往右平移,且正极导线投影下方的最大值也明显增大。考虑风速为8 m/s时,地面最大合成场强比无风增加了12.28 kV/m,且地面最大离子流密度是无风时的1.6倍。因此,考虑环境风速影响时,地面合成场强及离子流密度均会发生偏移和增大,且最大值不出现在导线投影下方。
从图13可知,当风速达到6 m/s时,负极导线投影处的地面合成场强峰值已经达到31.34 kV/m,离子流密度达到67.51 nA/m2。虽然导线对地高度为21 m,但是地面合成场强已经超过了我国规定的±800 kV直流输电线路的限值30 kV/m,此时合成场强峰值偏移了约1.07 m。当风速达到8 m/s时,正负极导线投影处的峰值分别为35.2 kV/m和33.23 kV/m,峰值分别偏移了约29.53 m和2.43 m。从图13和图14可知,随着水平风速的增大,地面合成场强和离子流密度的分布曲线和峰值均向右偏移,且正极导线下的合成场强和离子流密度比负极导线增大更明显。由于风速为水平向右,迫使空间电荷受风速影响往右迁移,且风速越大往右偏移也严重,特别是地面合成场强容易超过限值。因此在架设高压导线时,需要考虑不同地方存在的水平风速影响。对于风速较大地区,应该适当增加线路走廊宽度,以免背风面的地面合成场强超标。

图13 不同风速对地面合成场强的影响Fig.13 Influence of wind speed on ground level profile of electrical field strength

图14 不同风速对地面离子流密度的影响Fig.14 Influence of wind speed on ground level profile of ion current density
5 结论
(1)基于上流有限元方法求解泊松方程与离子电流密度方程耦合的HVDC输电线下离子流场问题。通过该方法与有解析解的算例比较,验证了方法的有效性,同时将该方法与考虑风速的单极HVDC导线模型比较,得出与文献近乎一致的结果。
(2)仿真计算时采用适当假设简化计算模型,计算区域采用不均匀三角元剖分,在保持计算精度的情况下减少了程序计算量。文中提出一种新的导线表面电荷密度更新公式,该公式能够充分利用每次迭代的导体表面节点场强值,考虑导体表面场强与起晕场强的关系,增加了一个修正系数。
(3)通过计算实际的双极HVDC导线离子流场问题,得出提高导线对地高度可以有效抑制地面最大合成场强和离子流密度。考虑风速时,地面合成场强和离子流密度均会比无风时增大,且最大值会发生偏移。因此,在实际架设高压直流输电线路时应当考虑当地的环境风速影响。
[1]焦彦军,于江涛,王增平(Jiao Yanjun,Yu Jiangtao,Wang Zengping).计算架空线路分布参数的新方法(New calculation method of overhead transmission line distributed parameters)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2015,27(4):55-60.
[2]Sarma M P,Janischewsky W.Corona loss characteristics of practical HVDC transmission lines-1[J].IEEE Trans on Power Apparatus and Systems,1970,89(5):860-867.
[3]Johnson G B.Degree of corona saturation for HVDC transmission lines[J].IEEE Trans on Power Delivery,1990,5(2):695-707.
[4]甄永赞,崔翔,罗兆楠,等(Zhen Yongzan,Cui Xiang,Luo Zhaonan,et al).直流输电线路三维合成电场计算的有限元方法(FEM for 3D total electric field calculation near HVDC lines)[J].电工技术学报(Transactions of China Electrotechnical Society),2011,26(4):153-160.
[5]袁海燕,傅正财(Yuan Haiyan,Fu Zhengcai).基于有限元法的±800 kV特高压直流输电线路离子流场计算(Corona ionized field analysis of±800 kV HVDC transmission lines)[J].电工技术学报(Transactions of China Electrotechnical Society),2010,25(2):139-146.
[6]Du Zhiye,Huang Guodong,Ruan Jianjun,et al.Calculation of the ionized field around the DC voltage divider[J].IEEE Trans on Magnetics,2013,49(5):1933-1936.
[7]Zhen Yongzan,Cui Xiang,Lu Tiebing,et al.High efficiency FEM calculation of the ionized field under HVDC transmission lines[J].IEEE Trans on Magnetics,2012,48(2):743-746.
[8]Kapzow N A.Elektrische Vorgänge in Gasen und im Vakuu[M].Berlin:VEB Deutscher Verlag der Wissenschaften,1955.
[9]Takuma T,Ikeda T,Kawamoto T.Calculation of ion flow fields of HVDC transmission lines by the finite element method[J].IEEE Trans on Power Apparatus and Systems,1981,100(12):4802-4810.
[10]Takuma T,Kawamoto T.A very stable calculation method for ion flow field of HVDC transmission lines[J].IEEE Trans on Power Delivery,1987,2(1):189-198.
[11]Lu Tiebing,Feng Han,Cui Xiang,et al.Analysis of the ionized field under HVDC transmission lines in the presence of wind based on upstream finite element method[J].IEEE Trans on Magnetics,2010,46(8):2939-2942.
[12]甄永赞,崔翔,罗兆楠,等(Zhen Yongzan,Cui Xiang,Luo Zhaonan,et al).直流输电线下存在建筑物时合成电场计算的有限元方法(Finite element method for calculating total electric field of HVDC lines with underneath building)[J].中国电机工程学报(Proceedings of the CSEE),2011,31(9):120-125.
[13]罗兆楠,崔翔,甄永赞,等(Luo Zhaonan,Cui Xiang,Zhen Yongzan,et al).直流线路邻近建筑物时合成电场的计算方法(Calculation method for the ionized field under HVDC transmission lines with building nearby)[J].中国电机工程学报(Proceedings of the CSEE),2010,30(15):125-130.
[14]周象贤,卢铁兵,崔翔,等(Zhou Xiangxian,Lu Tiebing,Cui Xiang,et al).基于有限元与有限体积法的直流输电线路合成电场计算方法(A hybrid method for the simulation of ion flow field of HVDC transmission lines based on finite element method and finite volume method)[J].中国电机工程学报(Proceedings of the CSEE),2011,31(15):127-133.
[15]冯晗(Feng Han).高压直流输电线路离子流场计算及其工程应用(Calculation of the ionized field under high voltage direct current transmission lines and engineering application)[D].保定:华北电力大学电气与电子工程学院(Baoding:School of Electrical and Electronic Engineering,North China Electric Power University),2006.
[16]Peek F W.Dielectric Phenomena in High-Voltage Engineering[M].New York:McGraw-Hill Book Company,1929.
[17]崔翔,周象贤,卢铁兵(Cui Xiang,Zhou Xiangxian,Lu Tiebing).高压直流输电线路离子流场计算方法研究进展(Recent progress in the calculation methods of ion flow field of HVDC transmission lines)[J].中国电机工程学报(Proceedings of the CSEE),2012,32(36):130-141.
[18]Janischewskyj W,Gela G.Finite element solution for electric fields of coronating DC transmission lines[J].IEEE Trans on Power Apparatus and Systems,1979,98(3):1000-1012.
[19]Hara M,Hayashi N,Shiotsuki K,et al.Influence of wind and conductor potential on distribution of electric field and ion current density at ground level in DC high voltage line to plane geometry[J].IEEE Trans on Power Apparatus and Systems,1982,101(4):803-814.
[20]Yu Ming,Kuffel E.New algorithm for evaluating the fields associated with HVDC power transmission lines in the presence of corona and strong wind[J].IEEE Trans on Power Apparatus and Systems,1992,29(2):1985-1988.
[21]余峰(Yu Feng).高压直流输电线下合成场强及离子流密度的计算(Calculation of ground level total electric field strength and ion current density under HVDC transmission lines)[D].北京:中国电力科学院(Beijing:China Electric Power Research Institute),1998.
Calculation of Ionized Field under HVDC Transmission Lines Considering the Influence of Wind Speed and Wire Height
XU Songzhi1,WANG Feng1,LI Min1,DENG Xiao1,2,XIE Wangjun1,CHEN Xiaolin1
(1.College of Electrical and Information Engineering,Hunan University,Changsha 410082,China;2.Laboratory for Electromagnetic Environment Monitoring and Modeling of Near Earth Space(Changsha University of Science and Technology),Changsha 410114,China)
In order to predict the electromagnetic environment under high voltage direct current(HVDC)transmission lines,the distribution of ionized field under different conditions is calculated.With Kaptzov hypothesis,the potential near artificial boundary is calculated by charge simulation method,and the electric field generated by space charge is obtained using Poisson equation.Moreover,a new updating formula of space charge density is proposed,and the equation of ion current density is solved by upstream finite element method.The validity of the proposed algorithm is verified by calculating the coaxial cylindrical electrode electric field,and its reliability is verified by solving the model of monopolar HVDC transmission lines considering wind speed.Finally,the ionized field of bipolar HVDC transmission lines under the influence of different heights and wind speeds is calculated,showing that both height and wind have a great influence on the maximum ground level profiles of field and ion current density,which are prone to shift due to wind.
high voltage direct current(HVDC);ionized field;wire height;wind speed;upstream finite element method
TM723
A
1003-8930(2016)12-0057-07
10.3969/j.issn.1003-8930.2016.12.010
许松枝(1990—),男,硕士研究生,研究方向为高电压试验与测试技术、电力设备故障诊断与在线监测技术。Email:xusongzhi1990@126.com
汪 沨(1972—),男,博士,教授,博士生导师,研究方向为高电压试验与测试技术、气体放电及其应用技术、电力设备故障诊断与在线监测技术。Email:wangfeng55@263.net
李 敏(1989—),男,硕士研究生,研究方向为特高压直流输电线路电磁场数值计算。Email:liminzhenqi@163.com
2015-05-08;
2016-06-07
教育部新世纪优秀人才支持计划资助项目(NCET-11-0130);长沙理工大学近地空间电磁环境监测与建模湖南省普通高校重点实验室开放基金资助项目(20150101)

