基于双端数据和算法融合的输电线路故障测距新方法
罗 毅,田吉华
(华北电力大学控制与计算机工程学院,北京 102206)
基于双端数据和算法融合的输电线路故障测距新方法
罗 毅,田吉华
(华北电力大学控制与计算机工程学院,北京 102206)
针对输电线路故障测距中工频法和行波法在不同情况下的缺点,本文提出了一种基于双端数据和算法融合的输电线路故障测距的新方法。首先根据故障发生的位置将输电线路划分为5个区间,利用双端数据结合双端不同步工频法进行初步测距,确定故障发生的区段,为行波法识别行波波头提供可靠性保证;然后根据工频法确定的故障区段采用不同的测距策略,利用波头到达时间与波速、线路长度之间的关系建立方程组消除波速不准的影响,同时引入比率变量表示测距结果以降低因线路长度变化造成的影响,进而提高了测距的准确性和可靠性。仿真实验表明了算法的有效性。
输电线路;故障测距;双端数据;算法融合;工频法;行波法
输电线路是电力系统中发生故障频率最高的地方。准确的故障测距技术可以减轻巡线负担,加快线路恢复供电,提高电力系统稳定性[1-3]。因此,提高故障测距的准确性和可靠性对电力系统具有重要的意义。
输电线路故障测距已成为国内外热门的研究课题之一。文献[4]利用故障相电路和零序等值电路提出了一种单端工频故障测距法。文献[5]使用基于分布参数模型的单端测距算法,提出适用于单相接地的单端相位测距法和幅值测距法。文献[6]单端行波法测距利用波速和行波的时间差计算故障距离。文献[7]将单端行波法和常规量测距法相结合,利用两种方法进行优势互补。文献[8-9]采用双端行波测距法,配备全球定位系统GPS(global positioning system)进行同步采样,充分利用了线路两端的数据。
由上述分析可知,分布参数模型更接近实际输电线路的运行状况;单端工频法无法从根本上避免故障位置、过渡电阻等因素的影响,存在原理上的劣势;行波法可以从原理上杜绝这些因素的影响,但同时也引入新的影响因素,如波速、时间误差、线路长度等;双端行波法虽在原理上有绝对的优势,但是实现中受GPS同步装置的精度影响较大,经济造价较高,未能很好地发挥双端数据的优势。组合算法是一个很好的尝试,但只利用单端数据,在区间确定和波头的识别中存在精度问题。
综上所述,本文提出了一种基于双端数据的工频-行波组合算法。首先,采样线路两端数据结合双端不同步工频法进行初步测距,充分利用线路两端数据,且避免使用GPS同步装置,降低故障测距设备造价,确定故障点所在区间为行波法判断反射波极性提供依据。然后,在初步测距的基础上,利用不计波速和线路长度影响的行波法进行精确测距,降低输电线路受环境温度、气候条件影响导致的测距误差。
1 测距算法原理
1.1 工频法
工频法是在系统运行方式确定和输电线路参数已知的条件下,根据故障时测距装置测量到的电压、电流,计算出所需特征量,然后依据输电线路长度与该特征量的关系,求出装置安装处到故障点的位置[10]。
图1中,UM、UN为线路两端的三相电源,其母线处安装有测量装置;F为故障发生处;DMf为故障距离。故障发生时可通过线路两端测得的电压和电流,按照双端不同步的故障测距原理,消除过度电阻对测量精度的影响,且无需GPS同步设备,大大降低设备方面的资金投入。同时,双端不同步算法在保证可靠性的同时比单端法具有更好的准确性,能满足初步测距需求。
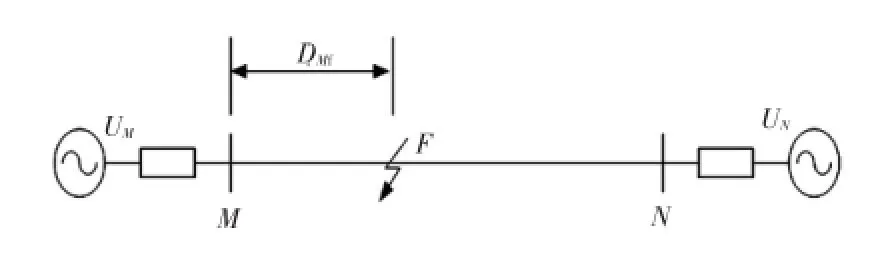
图1 双端电源系统三相输电线路Fig.1 Three-phase transmission line of double-ended power system
1.2 行波法
行波法是通过准确识别故障行波到达的时间差值来计算故障距离[11],原理如图2所示。
输电线路F处故障时,产生沿输电线路向两端母线传播的故障行波,tM1、tN1为到达M、N两端的时刻。由于阻抗不连续点的存在,故障行波在对端母线和故障点经折射和反射产生折射波和反射波,tM2、tM3为故障点反射波和对端母线折射波到达时间。行波法由于原理上的优势使得该方法测距精度高,但在近端测距时可靠性差,结合工频法的初步测距可提高测距的可靠性。
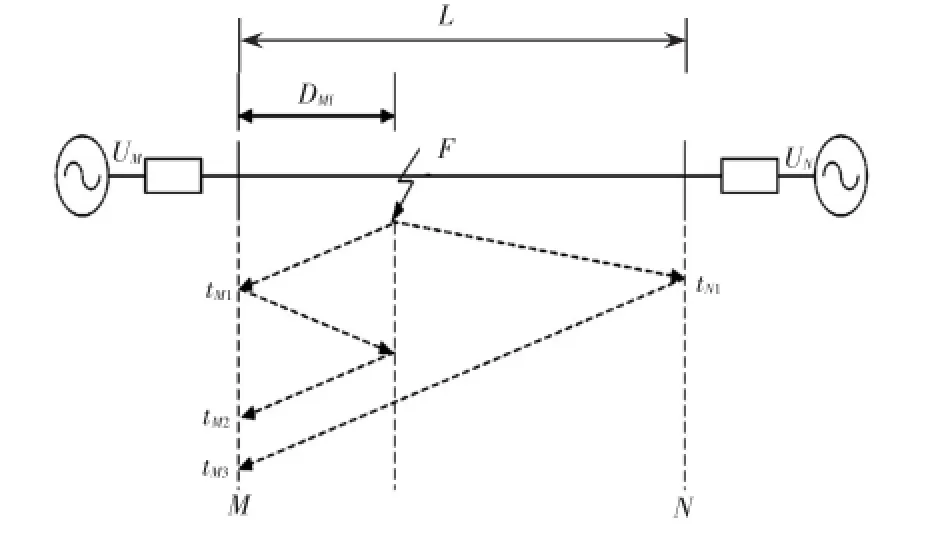
图2 故障行波折射、反射Fig.2 Refraction and reflection of traveling wave caused by fault
1.3 基于双端数据的组合算法
本文所用算法,首先利用电压、电流的工频特征量求得初步故障距离DMf1及区间。当线路没有发生故障时,有

式中:δ为M、N两端采样不同步角;UMj、IMj分别为线路M端的电压、电流;UNj、INj分别为线路N端的电压、电流;为传播常数;为输电线路的波阻抗;j= 0、1、2,分别表示零序、正序、负序;L为线路长度。
当线路发生故障时,利用对称分量法中正序分量在任何类型故障下都存在的特点,根据电路理论及长线方程原理,有
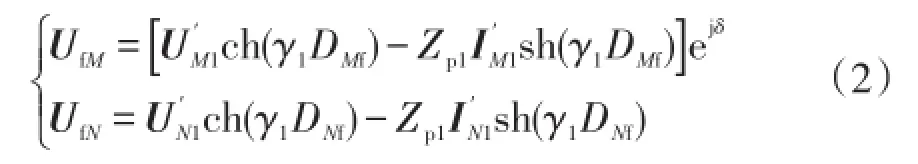
由于输电线路上电压具有连续性,所以在故障点处电压幅值相等,即同时将式(1)得到的UN1e-jδ表达式,代入式(2)消除不同步角的影响,可得
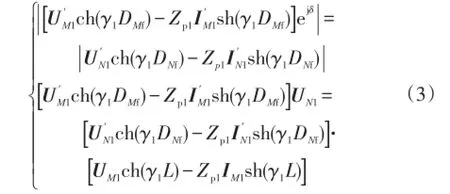
由此可求出故障距离公式为

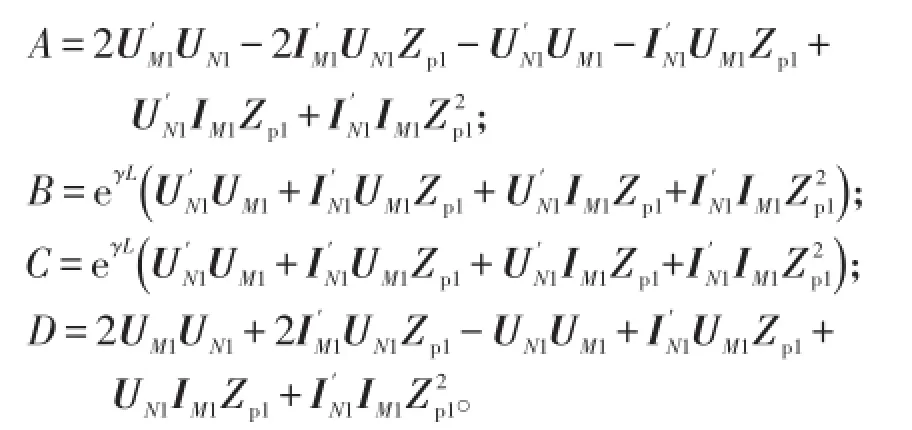
根据式(4)可得初步测距结果,但在实际运行的极端情况下会出现线路某一端因设备或传输等原因导致采集不到数据的情况,此时双端阻抗法将失效。因此本文算法设计在此种特殊情况下采用基于一端电气量的测量阻抗法进行测距,故障距离可由式(5)计算得出。
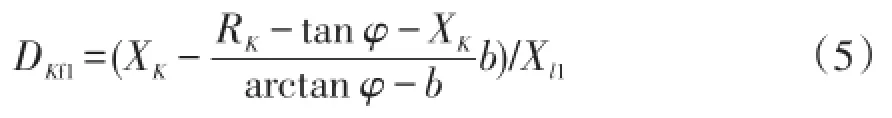
式中:Xl1为线路单位长度正序电抗;φ为线路正序阻抗角;a+jb=IKf/IK;RK+jXK=UK/IK为测量阻抗;K为M或N端电气量;IKf为故障分量电流;IK、UK分别为测量电流和测量电压。
计算得到的初步测距结果DMf1,用来划分故障点的线路区间,为了更加明确地划分故障区段,将整条输电线路划分为5个区段,如表1所示。

表1 输电线路区段Tab.1 Segments of transmission line
在初步测距结束后,取M和N端的故障电流进行小波变换求出行波前3个奇异点对应的时间,结合初步测距所确定的区间对各个波头属性进行判断[12-14],根据区段的不同采用不同的行波测距公式。由于输电线路运行条件复杂多变,使得行波波速v的准确计算比较困难,往往产生较大的误差[15],因此本算法采用不受波速影响的测距方法。同时,为了避免线路长度变化对测距结果的影响,令k=DMf/L为故障距离占线路全长的比例,各区段的具体测距公式如下:
(1)当故障点属于类型Ⅰ,即故障点离M端较近时,则可根据图2所示的行波折射、反射原理测距,建立方程组为

式(6)中两个方程相比可消除波速v和线路长度L,得

(2)当故障点属于类型Ⅱ,即故障点离N端较近时,则可根据图3所示的行波折射、反射原理测距。

图3 类型Ⅱ故障行波折射、反射示意Fig.3 Refraction and reflection of traveling wave caused by typeⅡfault
建立方程组为

式(8)中两个方程相比可消除波速v和线路长度L,得

(3)当故障点属于类型Ⅲ,即故障点位于M端和N端中间区域时,由于计算误差的存在,这个区段的划分是考虑当工频法所得结果为线路中点时,不能轻易地将故障距离x确定为,这是本算法分区思想优越性的体现。当发生类型Ⅲ故障时,需使用行波法做进一步验证,若则该点必定在中点处;若则当时采用公式(7)来求解故障距离,当时采用公式(9)来求解故障距离。
(4)当故障点属于类型Ⅳ,即故障点紧靠M端时,由于行波法的缺陷就是近端测距不准确,因此距离公式(7)不再适用。此时,初步测距优势便可更好地发挥,因为近端在25%的范围内,则M端测得的前4个奇异点时间分别是故障点向M端传播行波到达时间tM1、故障点反射波到达时间tM2、故障点2次反射时间tM3及对端母线反射波到达时间tM4。根据图4所示的行波折射、反射原理,可建立行波折反射方程组为
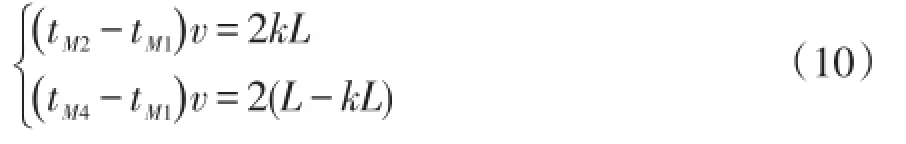
式(10)中两个方程相比可消除波速v和线路长度L,得

(5)当故障点属于类型Ⅴ,即故障点紧靠N端,原理与类型Ⅳ相同,根据图5所示的行波折射、反射原理测距。
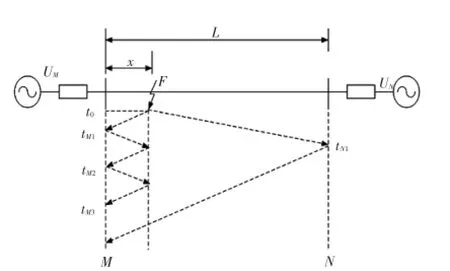
图4 类型Ⅳ故障行波折射、反射示意Fig.4 Refraction and reflection of traveling wave caused by typeⅣfault

图5 类型Ⅴ故障行波折射、反射示意Fig.5 Refraction and reflection of traveling wave caused by typeⅤfault
建立方程组为

式(12)中两个方程相比可消除波速v和线路长度L,得

在式(13)计算中,可在消除行波波速和因环境温度、气候条件变化导致线路长度变化造成的影响。若存在未检测到时间点或漏检时间点,则行波法所得结果与工频法所得结果有较大的偏差,此时可进行离线小波分析再次求取模极大值点。如果仍然失败仍可输出DMf1作为最终结果,故障测距流程如图6所示。
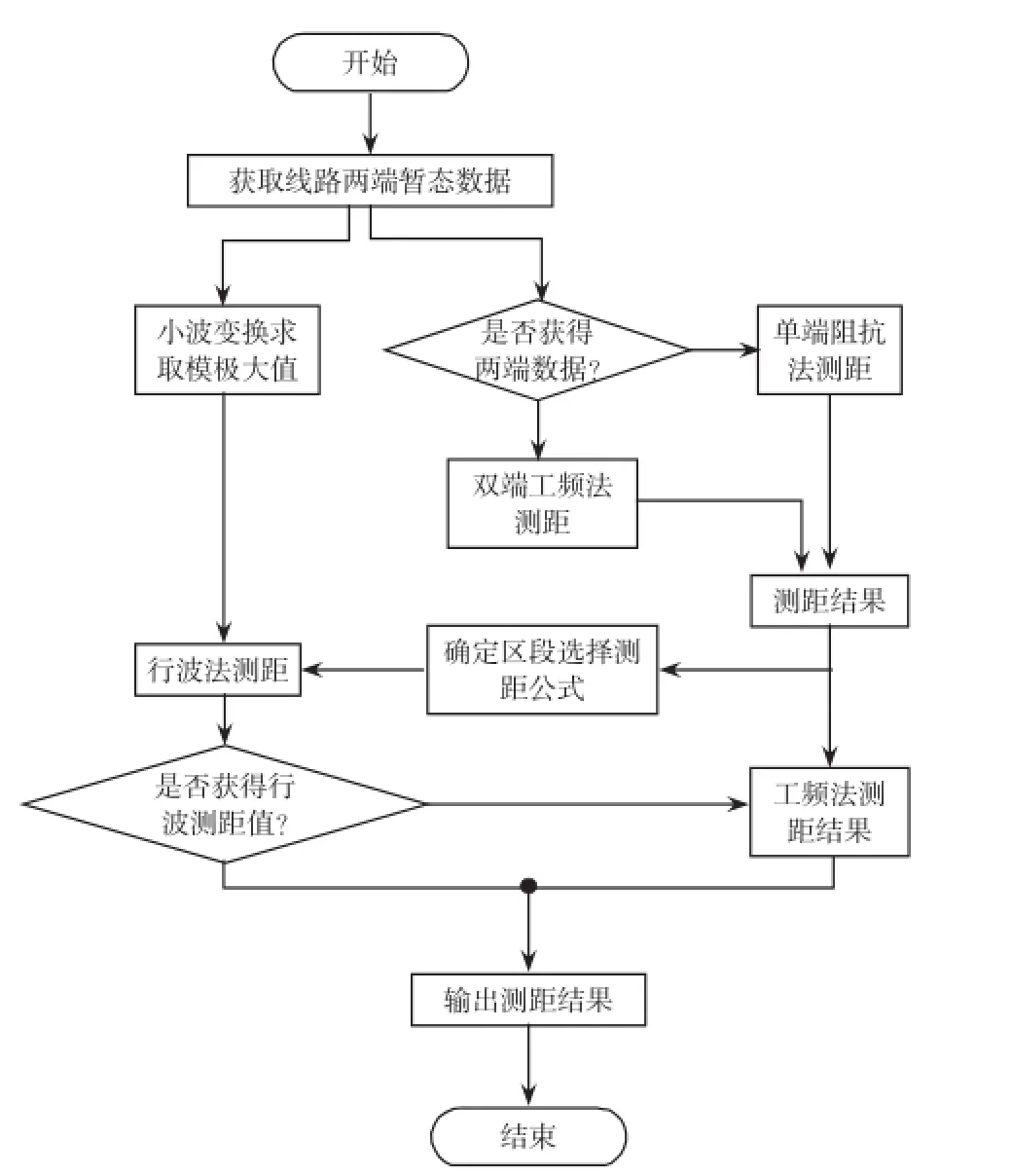
图6 故障测距流程Fig.6 Flow chart of fault location
2 仿真分析
2.1 输电线路的仿真模型
本文仿真中利用ATPDraw电磁暂态仿真软件建立输电线路仿真模型,如图7所示。

图7 ATPDraw建立输电线路仿真模型Fig.7 Simulation model of transmission line established by ATPDraw
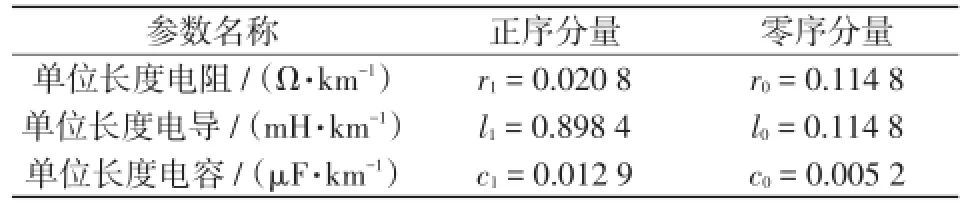
表2 仿真模型参数Tab.2 Parameters of simulation model
线路相关参数如表2所示,其中输电线路总长度为L=300 km,电压等级为U1=U2=500 kV,电源内阻参数为Z1=1.05+j43.18 W、Z2=1.06+j44.92 W,F点为线路发生故障位置,Rf为过渡电阻,开关K1、K2、K3和K4的闭合与断开的时间可以改变线路故障的类型,RLC为线路电阻、电感、电容参数。线路采用频率相关模型进行仿真,更接近实际,可信度更高。
2.2 故障仿真
高压输电线路的绝大多数故障属于短路故障,而其中单相短路最常发生,也最具代表性,因此本文以A相接地短路为例,设定当t=0.02 s时F点发生故障,距M端120 km,过渡电阻为200 Ω。
将所提取的仿真数据结合工频法进行初始测距,所得的结果为DMf1=0.396 4。根据表1知故障区间属于类型Ⅰ,针对该区间的故障采用测距公式(7)进行精确测距,利用M端电压值和电流值进行相模变换提取正向行波和模极大值如图8所示,得到最终测距结果为DMf2=0.399 7,如采用行波法测距所得的结果为0.399 6,而本文采用的组合算法所得的最终测距结果为DMf2=0.399 7,等效为实际距离误差缩小30 m。
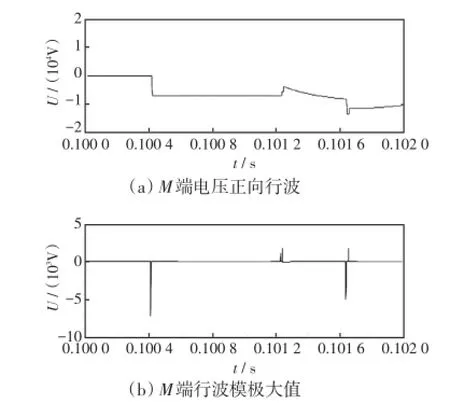
图8 M端电压正向行波及模极大值Fig.8 Forward traveling wave and maximum modulus at M end
本文在大量仿真实验的基础上验证了方法的有效性,通过改变故障距离、过渡电阻、输电线路长度,重复上述过程可得到一系列测距结果,如表3—表7所示。为了便于比较,同时进行工频法和行波法测距,并将二者测距结果换算为比例的形式列入表中,使比较更加直观。这两种方法的前提条件是线路长度等于300 km,线路各个参数等于给定值。表中k0为故障距离占线路全长的比例;k1、e1为工频法测距结果和误差;k2、e2为传统行波法测距结果及误差;k3、e3为本文组合算法测距结果和误差。测距误差公式为


表3 过渡电阻为200 Ω,线路长度为300 km时的测距结果Tab.3 Fault location results with 200 Ω transition resistance and 300 km line length
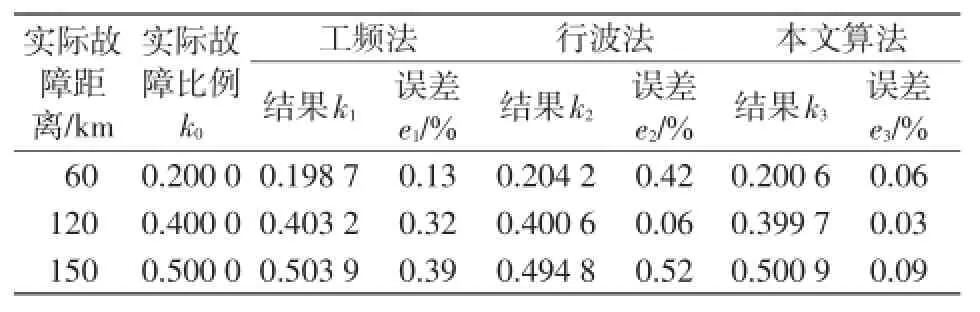
表4 过渡电阻为100 Ω,线路长度不变时的测距结果Tab.4 Fault location results with 100 Ω transition resistance and the same line length

表5 过渡电阻为300 Ω,,线路长度不变时的测距结果Tab.5 Fault location results with 300 Ω transition resistance and the same line length

表6 过渡电阻不变,线路长度变化+5%时的测距结果Tab.6 Fault location results with the same transition resistance and+5%error of line length
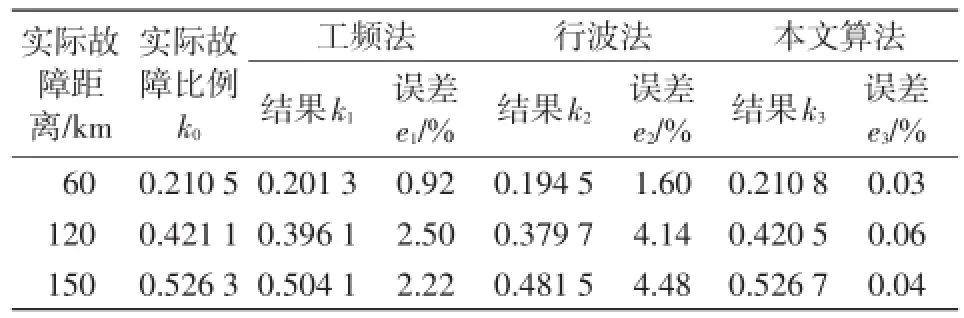
表7 过渡电阻不变,,线路长度变化-5%时的测距结果Tab.7 Fault location results with the same transition resistance and-5%error of line length
由仿真结果可以看出:
(1)表3、表4、表5中,在线路长度不发生变化的情况下而过渡电阻变化的情况下,工频法测距结果受到的影响较大,行波法测距结果较稳定但也稍逊于组合算法所得的测距结果。
(2)表3、表6、表7中,在过渡电阻不发生变化而线路长度发生5%的变化时,单独使用工频法和行波法所得测距结果受到影响,而本文算法得到的测距结果相对比较稳定。
(3)表3、表7中,本文提出的组合算法改善行波法近端测量不准的问题,而且受过渡电阻和输电线路长度变化的影响较小。
3 结语
通过分析工频法和行波法故障测距所存在的不足,如行波波速不确定和近端故障测距盲区等问题,提出了一种利用双端数据和算法融合的故障测距方法。通过仿真实验证明这种组合测距方法是可行的,并提高了测距精度。
本文所提方法能够充分利用故障发生时的数据特征量,并能克服单一测距算法测距时存在的不足,降低行波波速、过渡电阻及线路长度变化对测距结果的影响,对于线路故障准确定位和快速恢复具有重要意义。
[1]李一峰,陈平(Li Yifeng,Chen Ping).一种输电线路故障测距新方法(New method of fault location for transmission lines)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2008,20(4):125-128.
[2]何正友,钱清泉(He Zhengyou,Qian Qingquan).电力系统暂态信号的小波分析方法及其应用(The electric power system transient signal wavelet analysis method and its application)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2002,14(4):1-5,9.
[3]徐伟宗,唐昆明(Xu Weizong,Tang Kunming).利用行波经验模态分解实现线路故障测距(Fault location of transmission line by empirical mode decomposition of traveling wave)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2011,23(4):67-71.
[4]吴萍,张尧(Wu Ping,Zhang Yao).基于单端电气量的故障测距算法(Location using one-terminal data for transmission line)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2003,15(4):5-7,31.
[5]程伟,徐国卿,牟龙华(Cheng Wei,Xu Guoqing,Mu Longhua).基于分布参数模型的牵引网故障测距新算法(A novel fault location algorithm for traction network based on distributed parameter line model)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(6):63-66.
[6]束洪春,田鑫萃,董俊,等(Shu Hongchun,Tian Xincui,Dong Jun,et al).利用故障特征频带和TT变换的电缆单端行波测距(A single terminal cable fault location method based on fault characteristic frequency band and TT transform)[J].中国电机工程学报(Proceedings of the CSEE),2013,33(22):103-112.
[7]翟永昌(Zhai Yongchang).实用高压直流输电线路故障测距方法(Practical fault location method of HVDC power transmission line)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2008,20(5):70-73.
[8]曲广龙,杨洪耕,吴晓清,等(Qu Guanglong,Yang Honggeng,Wu Xiaoqing,et al).考虑电网拓扑结构的行波故障定位方法(Fault location with traveling wave considering network topological structure)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2013,25(6):117-122.
[9]徐伟宗(Xu Weizong).D型行波测距原理在辐射状配电线路中的应用(Application of D-type traveling wave location principle in radial distribution wires)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2012,24(5):138-143.
[10]陈铮,董新洲,罗承沐(Chen Zheng,Dong Xinzhou,Luo Chengmu).单端工频电气量故障测距算法的鲁棒性(Robustness of one-terminal fault location algorithms based on power frequency quality)[J].清华大学学报(自然科学版)(Journal of Tsinghua University(Science and Technology)),2003,43(3):310-313,317.
[11]徐湘忆,盛戈皞,刘亚东,等(Xu Xiangyi,Sheng Gehao,Liu Yadong,et al).输电线路分布式行波检测的故障定位方法(Fault location method for transmission line based on distributed traveling wave detection)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2012,24(3):134-138.
[12]林圣,何正友,陈鉴,等(Lin Sheng,He Zhengyou,Chen Jian,et al).基于行波时频特征的单端故障测距方法(A single terminal fault location method based on timefrequency characteristic of traveling wave)[J].电网技术(Power System Technology),2012,36(1):258-264.
[13]刘巍,湛大千(Liu Wei,Zhan Daqian).基于反向行波的故障测距(Fault location method on backward traveling wave)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2006,18(5):62-65.
[14]黄忠棋(Huang Zhongqi).采用行波固有频率的混合线路故障测距新方法(New method of fault location for hybrid lines by using traveling wave natural frequencies)[J].电力系统及其自动化学报(Proceedings of the CSUEPSA),2015,27(11):73-79.
[15]申文,刘亚东,盛戈皞,等(Shen Wen,Liu Yadong,Sheng Gehao,et al).输电线路实际运行状态对行波波速的影响(Influence of operating state of overhead transmission line on traveling wave velocity)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2014,26(9):12-16,29.
Transmission Line Fault Location Method Based on Double-ended Data and Algorithm-fusion
LUO Yi,TIAN Jihua
(School of Control and Computer Engineering,North China Electric Power University,Beijing 102206,China)
Considering the disadvantages of frequency method and traveling wave method,this paper presents a new transmission line fault location method based on double-ended data and algorithm-fusion.Firstly,the transmission line is divided into five intervals by the location of the fault,then frequency method can determine the fault zones using unsynchronized data at the two ends of line,which will guarantee the reliability for identifying the wave front of traveling wave.Secondly,a different location strategy will be applied according to the fault section,which can use the relationship among the arrival time of wave front,wave velocity and line length to establish an equation to eliminate the influence of wave speed.Moreover,the location result is replaced by ratio variable to reduce the influence of length change,which improves the accuracy and reliability.The simulation result indicates the effectiveness of the proposed method.
transmission lines;fault location;double-ended data;algorithm-fusion;frequency method;traveling wave method
TM77
A
1003-8930(2016)12-0001-06
10.3969/j.issn.1003-8930.2016.12.001
罗 毅(1969—),男,博士,教授,研究方向为复杂系统优化控制与决策。Email:lyphzh@163.com
2014-10-20;
2016-03-01
国家自然科学基金资助项目(61273144)
田吉华(1986—),男,硕士研究生,研究方向为智能输电线路及故障测距。Email:tjh254@163.com

