轨道非线性能量阱阻尼减震性能研究

王菁菁，浩文明

（湖南工业大学 土木工程学院，湖南 株洲 412007）

轨道非线性能量阱阻尼减震性能研究

王菁菁，浩文明

（湖南工业大学 土木工程学院，湖南 株洲 412007）

针对脉冲荷载优化得到的轨道非线性能量阱（轨道NES）的减震效果略差于调谐质量阻尼器（TMD）的问题，为了进一步提高轨道NES的减震性能，对轨道NES阻尼进行了分析，研究其对轨道NES减震性能的影响。模拟结果表明：通过改变轨道NES阻尼，可以提高其减震性能，在主体结构刚度发生变化时，轨道NES阻尼的改变可以改善其刚度鲁棒性。

非线性能量阱；数值模拟；阻尼；鲁棒性

0 引言

自1972年以来，结构控制技术被成功应用于降低结构在各类动力作用下的反应，如地震作用、风荷载等。墨西哥的Torre Mayor大厦是世界上首批使用阻尼器减震的高层建筑之一，它经受了2003年墨西哥7.6级地震的考验[1]，这也使结构被动控制方法得到了更多的认可。采用调谐质量阻尼器（tuned mass damper，TMD）减震是最常用的结构被动控制方法之一。当TMD频率调至与主体结构频率相近时，TMD可通过质量块的反相振动消耗能量。TMD高效减震的关键在于TMD调谐，即让TMD的自振频率与主体结构基频相同或相近[2]。

与TMD不同的是，非线性能量阱（nonlinear energy sink，NES）产生的非线性回复力，使其在结构动力特性发生变化时依然保持较好的减震效果。NES一方面作为阻尼器吸收和耗散能量，另一方面使能量在主体结构各模态间传递，将能量从低阶模态传递至耗能更快的高阶模态[3-4]靶能量传递）。

本文研究的轨道非线性能量阱（轨道NES）是一种新型的NES，由轨道和附加质量块组成。通过改变轨道形状可产生所需的非线性回复力，轨道与顶层相连，质量块沿着轨道运动。本文将推导轨道NES的回复力表达式和轨道NES系统的运动方程，并对附加轨道NES的两自由度主体结构在地震作用下的反应进行数值模拟，研究轨道NES阻尼对其减震性能的影响。

1 轨道非线性能量阱

轨道NES示意图如图1所示。轨道NES的非线性回复力由其特殊设计的轨道形状提供，轨道NES可以通过一组平行轨道上运行的小车实现。假设轨道NES质量块不转动且时刻保持与轨道接触，轨道NES的自由体受力图如图2所示。其中，mN为NES的质量，uN和vN分别为NES相对于轨道的水平位移和竖向位移，为轨道的水平位移，h(uN)为轨道的形状函数，Fnomal为NES作用在轨道上的法向反力，为轨道切线角度，g为重力加速度。

图1 轨道NES示意图Fig. 1 Configuration of track NES

图2 轨道NES的自由体受力图Fig. 2 Free body diagram of track NES

采用牛顿方法可得到轨道NES的运动方程[5]。由图2得水平方向上的力平衡方程为

竖直方向上的力平衡方程为

且有

将式（3）和式（4）代入力平衡方程式（1）和式（2），并联立式（5）可得

2 系统运动方程

采用如图3所示的轨道NES系统的结构模型来推导系统的运动方程。图中mi, ci, ki（i=1,2,…,n）分别表示第i层的质量、阻尼和刚度；cN表示轨道NES的阻尼。

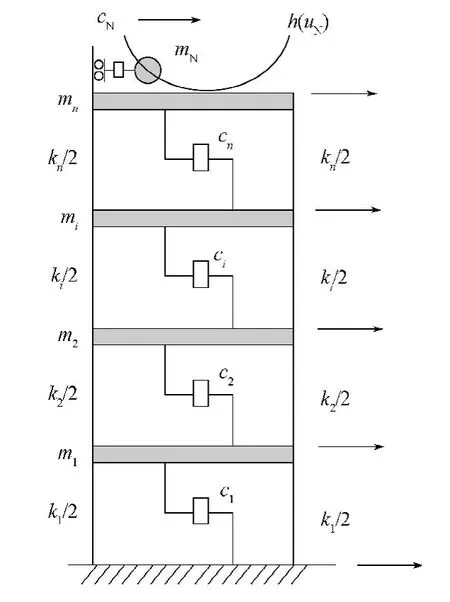
图3 轨道NES系统模型示意图Fig. 3 Schematic diagram of track NES system model

当未附加轨道NES时，该系统的运动方程可由以下矩阵形式表示

x为各层相对于地面的位移；

当附加轨道NES时，由于只有顶层与轨道NES相连，而其他层不直接与NES相连，因此它们的运动方程保持改变，可由以下矩阵形式表示

当顶层与轨道NES相连时，顶层的运动状态与轨道的运动状态相同，NES相对于顶层的位移可以由相对于轨道的位移代替。因此，对于整个系统中轨道NES的运动方程，只需将轨道加速度以顶层的绝对加速度代替，并加入阻尼力项，即可得到

式中xn表示第n层相对于地面的位移。

考虑NES的作用，在顶层的运动方程中添加非线性回复力和来自NES的阻尼力，可得到

式中：cnn, knn分别表示阻尼矩阵和刚度矩阵第n行、第n列的阻尼项和刚度项。

3 反应分析

NES的质量和轨道形状，采用文献[6-8]中使用脉冲荷载得到的优化结果；而阻尼根据相似试验取经验值，未经过优化。其中，。

轨道NES系统、TMD系统和锁住系统在4号地震下的顶层位移反应见图4。

图4 4号地震作用下100%刚度时的顶层位移反应Fig. 4 Top floor displacements with 100% stiffness under the action of No.4 earthquake

由图4可知，轨道NES系统的顶层位移峰值甚至超过了锁住系统，其减震性能明显不如TMD系统。

在4号地震作用下，主体结构刚度减小50%后的各系统的顶层位移反应见图5。由图5可知，轨道NES和TMD的减振性能均明显下降。

图5 4号地震作用下50%结构刚度时的顶层位移反应Fig. 5 Top floor displacements with 50% stiffness under the action of No.4 earthquake

4 轨道NES阻尼优化

为了提高轨道NES的减震性能，本文研究轨道NES阻尼对其减震性能的影响。在地震作用下的轨道NES优化阻尼，以及在原始阻尼和优化阻尼下的顶层位移均方根值见表1。

由表1可知：在不同的地震作用下，轨道NES最优阻尼产生了一定的波动，说明可以把调整NES阻尼作为改善其减震性能的一种手段。

7号地震在50%刚度时，轨道NES反而放大了地震的反应。这是由于优化阻尼过大，导致轨道NES的减振性能不能适应刚度的变化，可以考虑通过减小轨道NES阻尼来提高其刚度鲁棒性。如考虑优化阻尼为9.6 N·s·m-1。此时，在100%结构刚度时，轨道NES结构反应可以减小为33.85%；而当结构刚度下降50%时，轨道NES减小结构反应可以达到20.97%。

轨道NES系统、TMD系统和优化后的轨道NES系统，在4号地震作用下的顶层位移反应见图6。由图6可知，优化后轨道NES系统的最大顶层位移明显下降，优化后轨道NES的减震效果明显优于TMD系统。

表1 轨道NES系统顶层位移反应结果Table 1 Top floor displacement response results of track NES

图6 4号地震作用下100%刚度时阻尼优化前后的顶层位移反应Fig. 6 Top floor displacements before and after the damping optimization under the action of No.4 earthquake

轨道NES系统、TMD系统和优化后轨道NES系统，在主体结构刚度下降50%后的顶层位移反应见图7。从图中可以看出：优化后轨道NES的减震性能明显提高，在20 s左右，顶层位移已经降低至较低的水平，能够达到减震的效果。

轨道NES阻尼存在最优值使结构减震效果最佳，并能改善其刚度鲁棒性。因此，在以后的研究中，可以考虑通过调整轨道NES阻尼（如半主动方法）来改善其刚度鲁棒性。

图7 4号地震作用下50%刚度时阻尼优化前后的顶层位移反应Fig. 7 Top floor displacements with 50% stiffness before and after the damping optimization under the action of No.4 earthquake

5 结语

本文研究的轨道NES是一种被动的能量控制装置，它通过改变轨道形状产生所需的非线性回复力。因为通过脉冲荷载优化得到的轨道NES的减震效果略差于TMD，为了提高轨道NES的减震性能，研究了轨道NES阻尼对其减震性能的影响。研究结果表明：轨道NES阻尼存在最优值使其减震效果最佳，因此，可以通过调节轨道NES阻尼来提高其减震性能。当主体结构刚度发生变化时，最优阻尼依然可以提高轨道NES的减震性能，即可以通过改变轨道NES阻尼来改善其刚度鲁棒性。

[1]陈永祁，高 正，博 阳. 抗震阻尼器在墨西哥Torre Mayor高层建筑中的应用[J]. 钢结构，2011，26(1) ：50-54. CHEN Yongqi，GAO Zheng，BO Yang. Seismic Damper for the Torre Mayor High Rise Building at Mexico City[J]. Steel Construction，2011，26 (1) ：50-54.

[2]SADEK F， MOHRAZ B，TAYLOR A W, et al. A Method of Estimating the Parameters of Tuned Mass Dampers for Seismic Applications[J]. Earthquake Engineering & Structural Dynamics，1997，26(6) ： 617-635.

[3]MCFARLAND D M， BERGMAN L A， VAKAKIS A F. Experimental Study of Non-Linear Energy Pumping Occurring at a Single Fast Frequency[J]. International Journal of Non-Linear Mechanics，2005，40 (6) ：891-899.

[4]MCFARLAND D M，KERSCHEN G，KOWTKO J J，et al. Experimental Investigation of Targeted Energy Transfers in Strongly and Nonlinearly Coupled Oscillators [J]. The Journal of the Acoustical Society of America，2005，118 (2) ：791-799.

[5]CRAIG R R，KURDILA A J. Fundamentals of Structural Dynamics[M]. 2nd ed. Hoboken：Wiley，2006：396-404. [6]WANG J J，WIERSCHEM N，SPENCER B F，et al. Track Nonlinear Energy Sink for Rapid Response Reduction in-Building-Structures[J]. Journal of Engineering Mechanics，2015，141(1) ：1-10.

[7]AL-SHUDEIFAT M A， WIERSCHEM N， QUINN D D，et al. Numerical and Experimental Investigation of a Highly Effective Single-Sided Vibro-Impact Non-Linear Energy Sink for Shock Mitigation[J]. International Journal of Non-Linear Mechanics, 2013，52：96-109.

[8]WIERSCHEM N E. Targeted Energy Transfer Using Nonlinear Energy Sinks for the Attenuation of Transient Loads on Building Structures[D]. Illinois：University of Illinois at Urbana-Champaign，2013.

（责任编辑：邓光辉）

Study on the Trap Damping of Nonlinear Energy Sink for Seismic Reduction

WANG Jingjing，HAO Wenming
（School of Civil Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China）

In the light of the slight inferiority of the damping effect achieved by the nonlinear energy sink (track NES) under the pulse load optimization compared with that of the tuned mass damper (TMD), and with a view to further improving the damping performance of the track NES, an analysis has been made of the track NES and a research has been conducted on its effect on the damping performance. Simulation results show that track NES for seismic reduction can be improved by changing the track NES damping. With the structural stiffness of the primary structure having been altered, the robustness against the structural stiffness can be greatly improved by changing the damping of the track NES.

nonlinear energy sink；numerical simulation；damping；robustness

O328；O322

A

1673-9833(2016)05-0001-05

10.3969/j.issn.1673-9833.2016.05.001

2016-07-06

国家自然科学基金资助项目（51608190），湖南省教育厅科学研究基金资助项目（16C0485）

王菁菁（1986-），女，湖南株洲人，湖南工业大学讲师，主要从事结构控制方面的教学与研究，E-mail：plantplant0050@163.com