考虑可移动电荷的双栅隧穿场效应晶体管电流模型

孟庆之,李尊朝,关云鹤,张也非

(西安交通大学电子与信息工程学院,710049,西安)



考虑可移动电荷的双栅隧穿场效应晶体管电流模型

孟庆之,李尊朝,关云鹤,张也非

(西安交通大学电子与信息工程学院,710049,西安)

为了解决隧穿场效应晶体管(TFET)在强反型区表面势和漏电流精度下降的问题,建立了一种考虑可移动电荷影响的双栅TFET电流模型。首先求解考虑可移动电荷贡献的二维电势泊松方程,推导出表面势、电场的解析表达式;然后利用求得的电场表达式和Kane模型得到载流子的隧穿产生率;最后利用切线近似法计算隧穿产生率在隧穿区域的积分,建立了漏电流的简洁解析模型。利用器件数值仿真软件Sentaurus在不同器件参数下对所建模型进行了验证,仿真结果表明:考虑可移动电荷的影响能够提高强反型区漏电流模型的精度;在相同器件参数条件下,考虑可移动电荷的模型比忽略可移动电荷的模型精度提高了20%以上。

隧穿场效应晶体管;可移动电荷;表面势;漏电流;解析模型

随着特征尺寸趋近物理极限,金属氧化物半导体场效应晶体管(MOSFET)面临更加严峻的挑战,如短沟道效应加剧、泄漏电流过高以及60 mV/dec的亚阈值摆幅限制[1-5]等。研究表明,隧穿场效应晶体管(TFET)能有效地解决上述MOSFET问题。由于TFET有一个内建的隧穿势垒,因此它能有效地抑制短沟道效应,拥有更陡峭的亚阈值特性[6],并且在关态时隧穿势垒变窄,使得泄漏电流很小。由于TFET具有这些优点,从而被认为是最有希望取代MOSFET的候选器件之一,因此对TFET建立精确且可用于电路仿真的解析模型具有重要的意义。

建立TFET的电流模型,需要首先求解沟道二维泊松方程以获得表面电势和隧穿产生率的解析表达,再计算隧穿产生率在隧穿范围内的体积分。根据隧穿产生率在隧穿范围内积分的计算方法,将隧穿电流模型分为数值模型[7-9]和解析模型[6,10-14]。数值模型需要对隧穿产生率在沟道进行数值积分计算隧穿电流,其结果虽然较为精确,但计算量大,难以在电路仿真中使用。解析模型又分为平均电场法[10-13]和切线近似法[6,14]。平均电场法用最短隧穿路径上的平均电场代替隧穿范围内的电场分布,借助平均隧穿产生率与隧穿区域体积的乘积计算隧穿电流。由于隧穿区域内实际电场和隧穿产生率分布并不均匀[6-7],导致该模型精度不足。切线近似法将隧穿产生率在隧穿区域的积分用隧穿产生率曲线上若干点切线下三角形面积之和来近似,从而建立隧穿电流的解析模型。切线近似法的误差随着计算点数量的增加快速减少,因而具有较高的精度,并且该模型是一个连续的解析模型,可以应用于电路仿真中。

Vishnoi等人基于切线近似法为围栅和双栅TFET建立了隧穿电流解析模型[15],但没有考虑可移动电荷(载流子)的贡献,使该模型在高栅压下强反型区的精度受到影响。本文考虑可移动电荷对电场分布的影响,利用切线近似法对双栅TFET建立了漏电流解析模型。首先用电势叠加原理求解包含可移动电荷项的二维电势泊松方程,得到电场和隧穿产生率的解析表达式,再利用切线近似法对隧穿产生率积分建立漏电流解析模型。将采用本文解析模型的计算结果与采用二维数值仿真软件Sentaurus的仿真结果进行对比,在不同器件参数条件下验证了解析模型的有效性。仿真结果表明:考虑可移动电荷的影响能够提高强反型区漏电流类型的精度;在相同器件参数条件下,考虑可移动电荷的模型比忽略可移动电荷的模型精度提高了20%以上。

1 模型建立

1.1 电势模型

本节从双栅TFET的结构图出发,推导包含可移动电荷项的泊松方程,求解沟道电势和电场分布。

图1显示了N型对称双栅TFET的截面图。其中源区和漏区分别为P和N掺杂,为了避免仿真过程中出现不收敛问题,本征区沟道通常采用一定浓度(<1016mm-3)的弱掺杂[7,19],而在源掺杂浓度相同的情况下,当TFET处于关态(Vgs=0)时,弱P型沟道比弱N型沟道的TFET隧穿势垒宽度更大,能够获得更小的泄漏电流,因此本文采用弱P掺杂沟道。

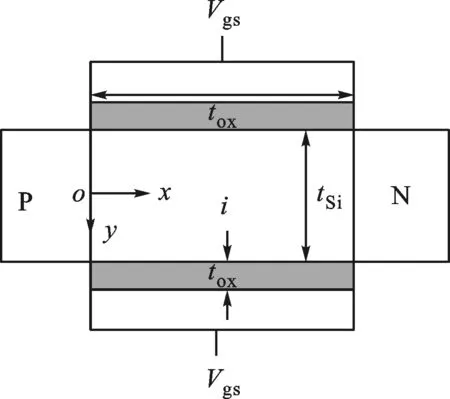
Vgs:栅压;L:沟道长度;tSi:硅层厚度;tox:栅氧化层厚度图1 N型对称双栅隧穿器件截面图

沟道内的电势分布由包含可移动电荷项的二维泊松方程描述[16]

(1)

式中:φ(x,y)为沟道内二维电势分布;εSi为硅介电常数;n和NA分别为沟道内反型层电荷浓度和P型掺杂浓度;ni为本征载流子浓度;Vt为热电势;φfn为电子准费米势。之所以引入准费米势来描述沟道中的电荷分布,是由于当源沟道之间有隧穿电流流过时,沟道中存在非局部电荷。仿真结果[11]表明,除了在源端附近外,准费米势沿沟道方向基本是常量。为了简化模型推导,通常将准费米势在整个沟道中取为常量[17],并且随后的仿真结果也证实了其正确性。为了便于求解,根据电势叠加原理[18],φ(x,y)可以表示为

(2)

式中:v(y)为一维泊松方程(3)的解;φ1(x,y)为二维拉普拉斯方程的解

(3)

(4)

首先对式(3)中v(y)求解,利用抛物线近似法[16],v(y)可以表示为

v(y)=a+by+cy2

(5)

将v(y)代入式(3)中,令y=tSi/2,利用边界条件得[16]

(6)

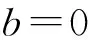
(7)

(8)

式中:Δφ=(φm-φs)/q为平带电压,其中φm和φs分别为栅极和半导体的功函数;tox为栅氧化层厚度;tSi为硅层厚度;εox为栅介质介电常数。对于给定的Vgs,即可确定c和a的值,进而确定v(y)的表达式。

接下来对式(4)二维拉普拉斯方程中的φ1(x,y)求解,φ1(x,y)可以写为

(9)

式中uL和uR分别为满足源和漏端边界条件的电势,uL和uR可分别写为[18]

(10)

(11)

特征值λn可由下式确定

(12)

uL、uR第一项系数的解为[17]

(13)

(λ1ctsi/π)tan(πtSi/2λ1))/(tSi/λ1+sin(πtSi/λ1)]

(14)

式中:φSC为源端和沟道的内建电势;φCD为沟道和漏端的内建电势。

利用式(12)求出对应的特征值λi,替换b1和c1表达式中的λ1,即可求得系数bi和ci(i=1,2,…,n)。事实上,对于对称双栅结构TFET,偶数阶系数b2,c2、b4,c4,…均为0,并且bi和ci随着i的增加衰减很快,因此电势模型只需保留第一项系数即可[18]

(15)

将y=tSi/2带入式(14),即可得到沿沟道方向的表面势模型

(16)

表面电场强度可对(15)式求导获得。由于隧穿电流与电场强度呈指数关系,电场强度的精度对电流的精度有很大的影响。为了获得更精确的电场分布,需要考虑电势模型的高阶项。数值仿真结果显示,当阶数n取至7时,电场模型与数值仿真结果已非常吻合。因此,表面电场分布为

(17)

1.2 电流模型

计算隧穿电流通常使用Kane模型[19]

(18)

Id=q∫GbtbtdV

(19)

式中:Gbtbt为隧穿产生率,代表单位体积单位时间产生的载流子数目;A、B为隧穿参数;E为电场强度;D为指数因子,对直接隧穿机制D=2,间接隧穿机制D=2.5[19],本文中所用的硅材料是间接带隙材料,因此取D=2.5;V代表沟道内载流子发生隧穿区域的体积。

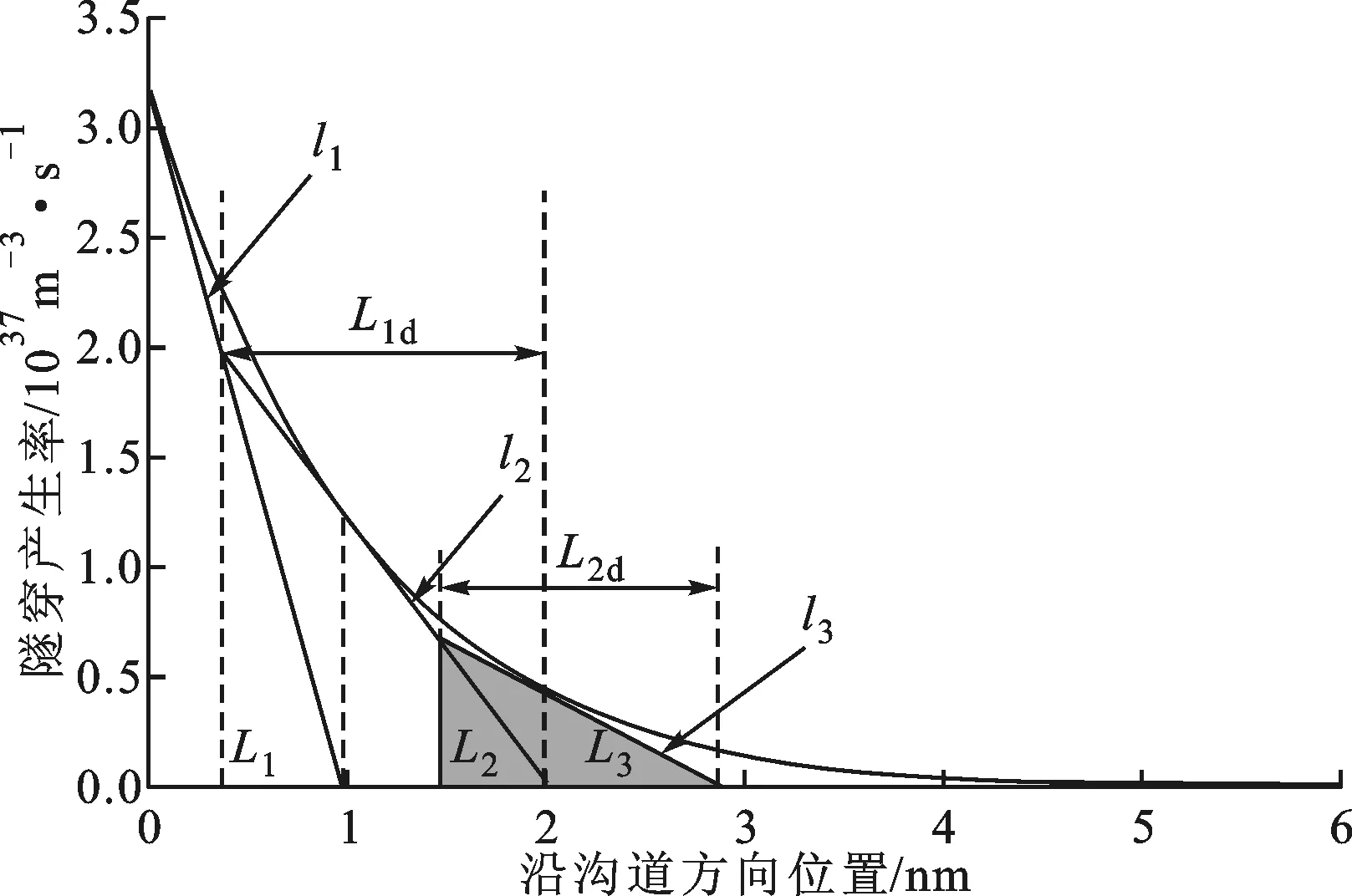
各器件参数为Vgs=1.4 V,Vds=0.5 V,tsi=10 nm,tox=1.5 nm,εox=7.5ε0。图2显示了源/沟道结附近的表面隧穿产生率Gbtbt沿沟道方向的变化曲线。Gbtbt沿沟的积分值即为图2a～图2e中Gbtbt曲线与坐标轴围成的面积,这里采用一种近似方法来计算该面积。如图2a所示,首先在x=0处作Gbtbt的切线l1,l1与x轴的截距记为L1,其计算公式为

(20)

l1下面阴影部分的三角形面积G1的计算式为

(21)

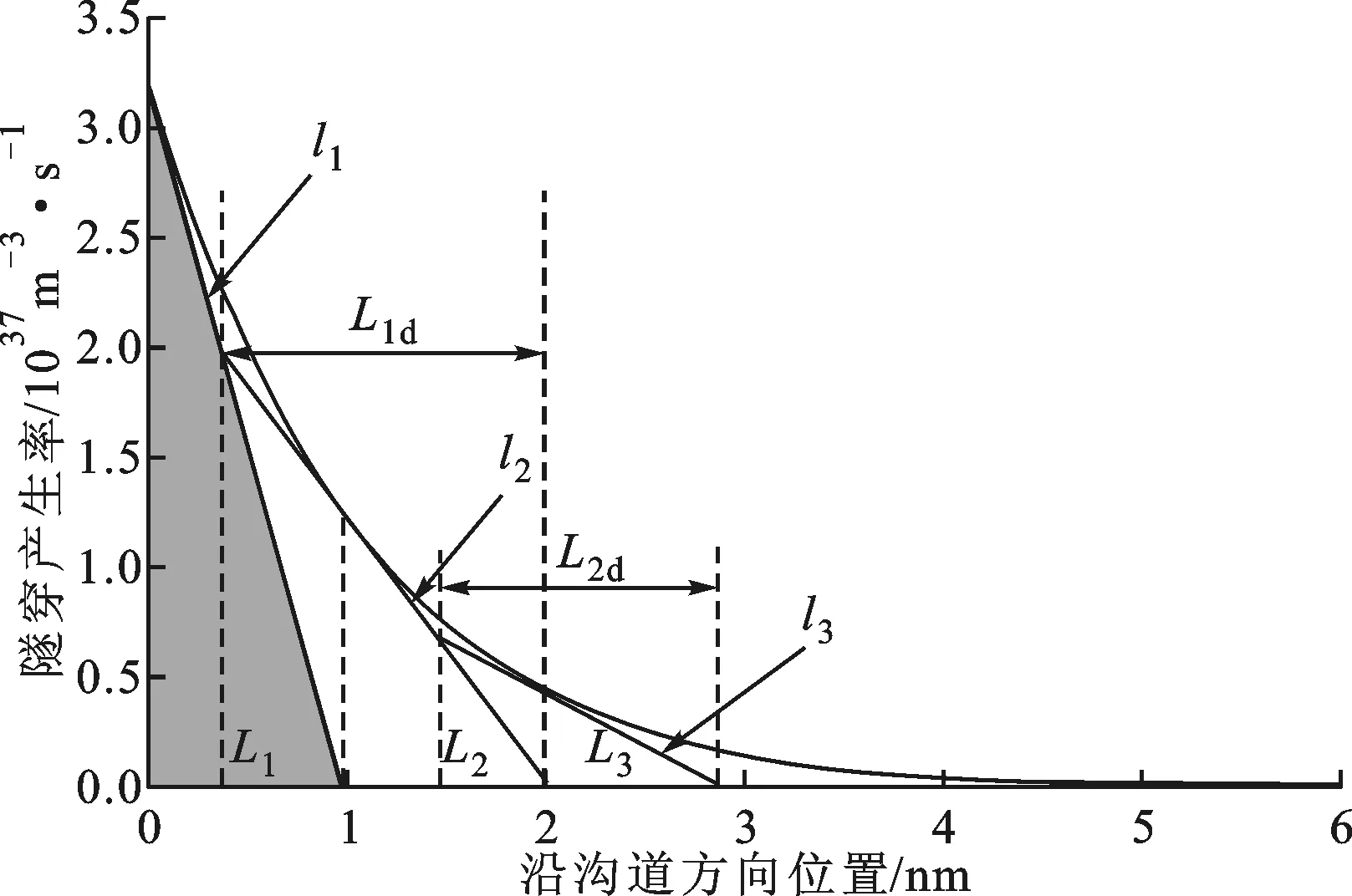
(a)阴影面积G1

(b)阴影面积G2

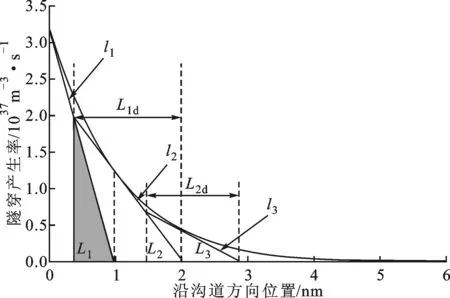
(c)阴影面积G1d

(d)阴影面积G3

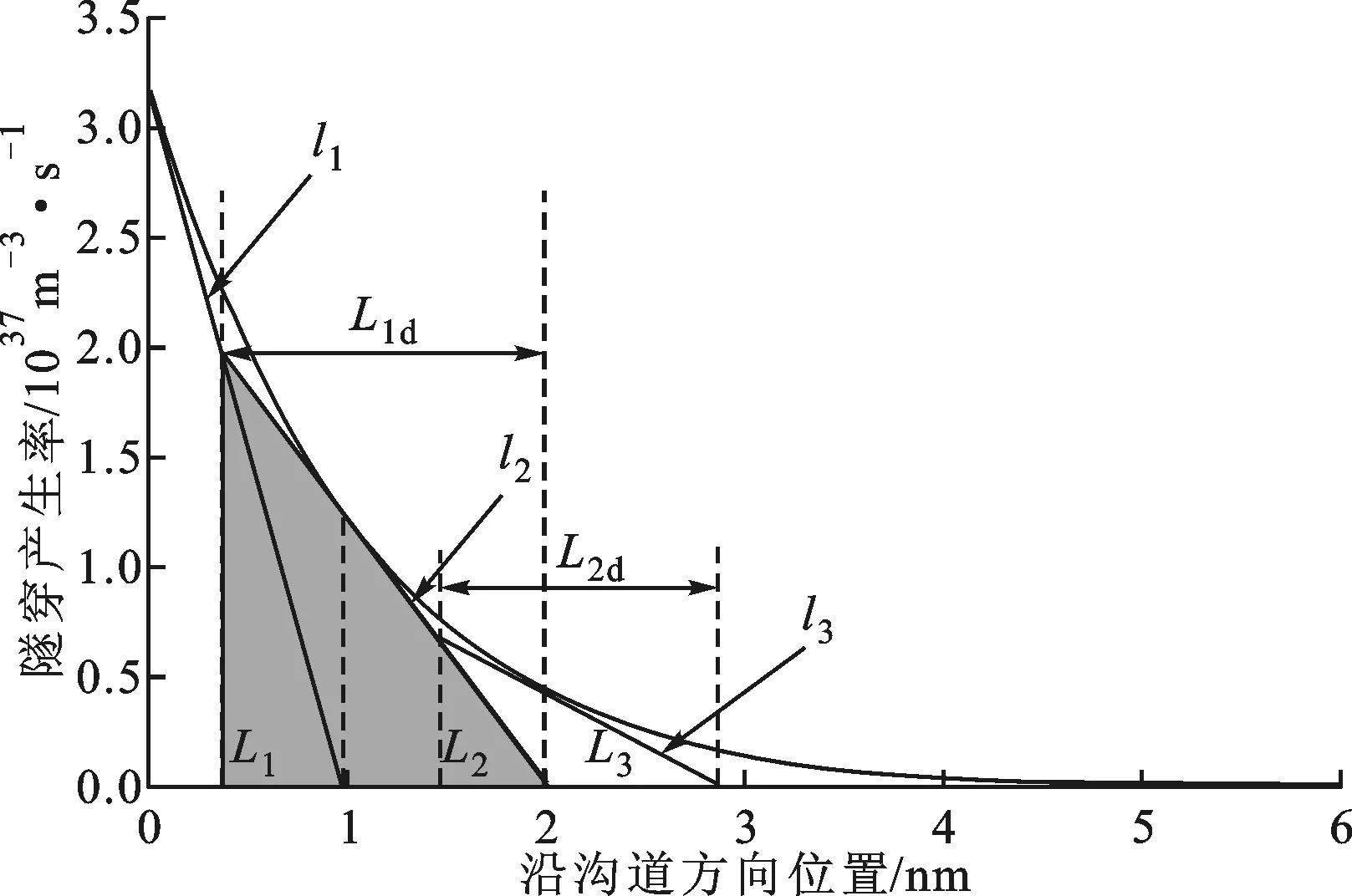
(e)阴影面积G2d图2 源/沟道结附近的表面隧穿产生率Gbtbt沿沟道方向的变化曲线及相应的阴影面积

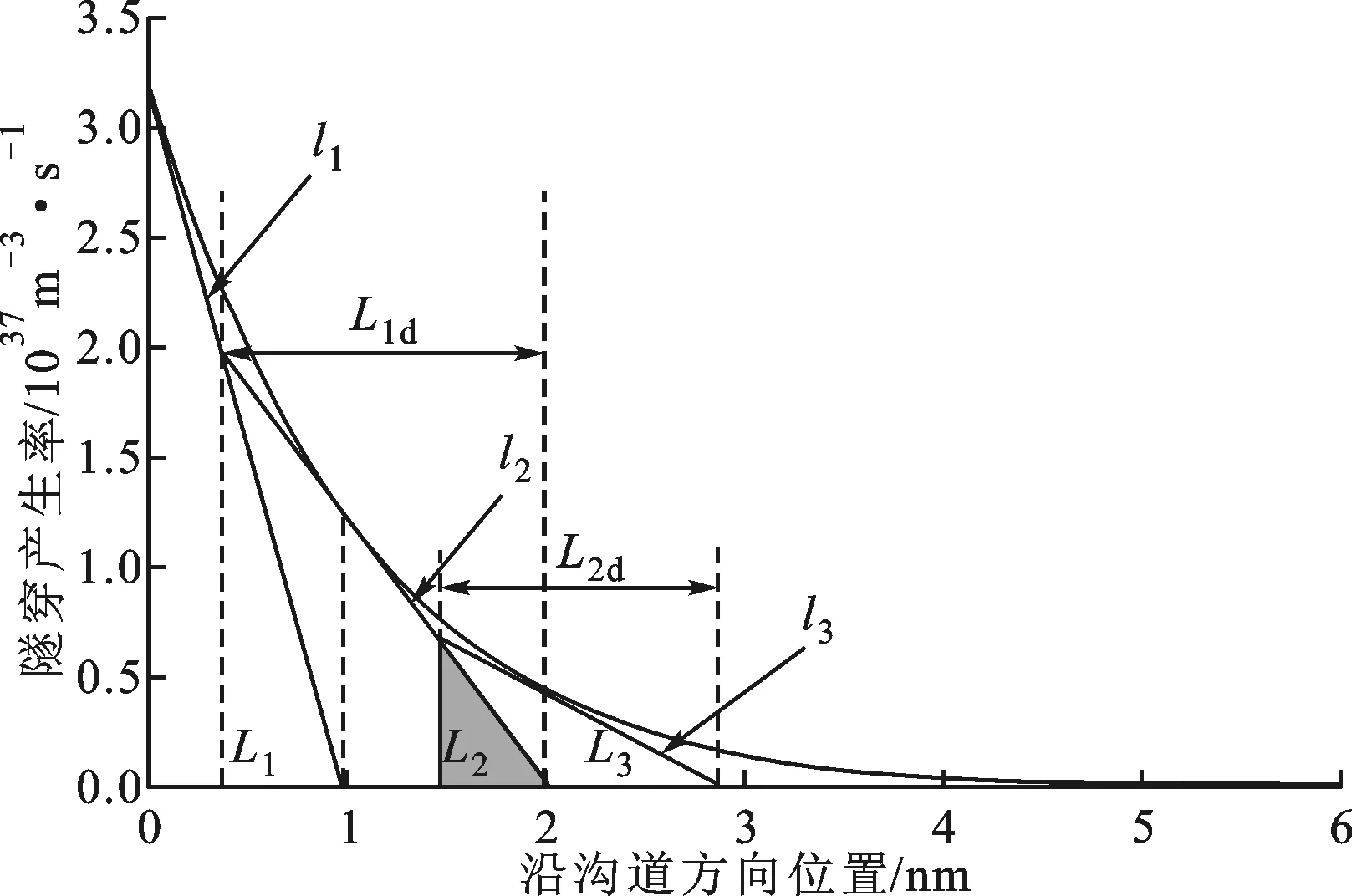
再在x=L1处作Gbtbt的切线l2,如图2b所示。l2与x轴的截距记为L1+L2,其中

(22)

l2下面阴影部分的三角形面积记为G2,其计算式为

(23)

式中

(24)

G1与G2重叠部分的面积记为G1d(图2c),计算式为

(25)

继续在x=L1+L2处作Gbtbt的切线l3,如图2d所示,l3与x轴的截距记为L1+L2+L3,其中

(26)

l3下面阴影部分的三角形面积记为G3,计算式为

(27)

(28)

G2与G3重叠的部分记为G2d(图2e),计算式为

(29)

重复此步骤,归纳出作了n次切线后的通项式

(30)

(31)

(32)

(33)

重复n次后隧穿产生率沿沟道方向总的积分GT的表达式为

(34)

在实际计算中,只要做到第4次就已经很接近真实值了[6,14],因此总阴影面积GT为

GT=G1+G2+G3+G4-G1d-G2d-G3d

(35)

隧穿区域的厚度可取反型层的厚度[6,14]。综上所述,隧穿电流为

Id=qtinvGT

(36)

式中:tinv为反型层厚度。该电流模型是一个连续的解析模型,可应用于电路仿真中。

2 模型验证和讨论

下面将本文所建电流解析模型与二维数值仿真软件Sentaurus的仿真结果进行对比,验证本文模型在不同器件参数条件下的有效性,并给出了文献[14]所建立的忽略可移动电荷的解析模型结果。本文使用Kane带带隧穿模型,隧穿参数为A=4×1014,B=1.9×107V/cm[20]。源区和漏区N型掺杂浓度为1018cm-3,沟道P型掺杂浓度Na=1016cm-3,栅极功函数φm=4.5 eV。

图3显示了栅压从0～1.6 V每隔0.4 V表面势沿沟道方向的变化曲线,器件各参数为tsi=10 nm,tox=2 nm,εox=3.9ε0,Vds=0.5 V,L=50 nm。从图中可以观察到:考虑可移动电荷模型与数值仿真结果吻合很好;当栅压不大时,文献[14]所建立的忽略可移动电荷模型与数值仿真结果基本吻合;当栅压逐渐增大时(Vgs≥0.8 V),文献[14]模型逐渐偏离数值仿真结果。其原因是:当栅压不大时,可移动电荷的影响可以忽略,而当栅压逐渐增大时,沟道进入强反型区,可移动电荷密度随栅压的增加快速增加,增加的栅压主要降落在栅氧化层,表面势的增加越来越缓慢,并逐渐趋于饱和值[21],而不是文献[14]模型所得到的表面势随栅压继续较快增加。

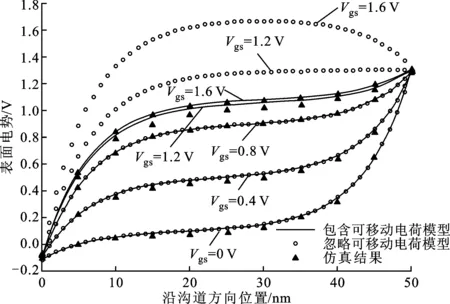
图3 不同栅压下的表面电势曲线

图4显示了2种模型下的转移特性曲线。与表面势情况类似,考虑可移动电荷模型及数值仿真结果吻合很好;当栅压不大时,文献[14]所建立的忽略可移动电荷模型与数值仿真结果基本吻合;当栅压逐渐增大时(Vgs≥0.8 V),文献[14]模型逐渐偏离数值仿真结果。其原因是当栅压不大时,可移动电荷的影响可以忽略,而当栅压逐渐增大时,可移动电荷密度随栅压的增加快速增加,表面势的增加越来越缓慢,并逐渐趋于饱和值,源端附近的电场及线漏电流也逐渐趋向饱和,而文献[14]模型所得到的线漏电流随栅压继续较快增加。因此,在强反型区考虑可移动电荷模型比文献[14]的模型更精确。如Vgs=1 V时,仿真所得的线漏电流为1.931 2×10-6A/μm,文献[14]的模型所得的电流值与仿真值相差0.683 7×10-6A/μm,占仿真值的35.40%,而考虑可移动电荷模型所得的电流值与仿真值相差0.285 6×10-6A/μm,占仿真值的14.79%,与文献[14]相比,考虑可移动电荷模型精度提高了20.61%。

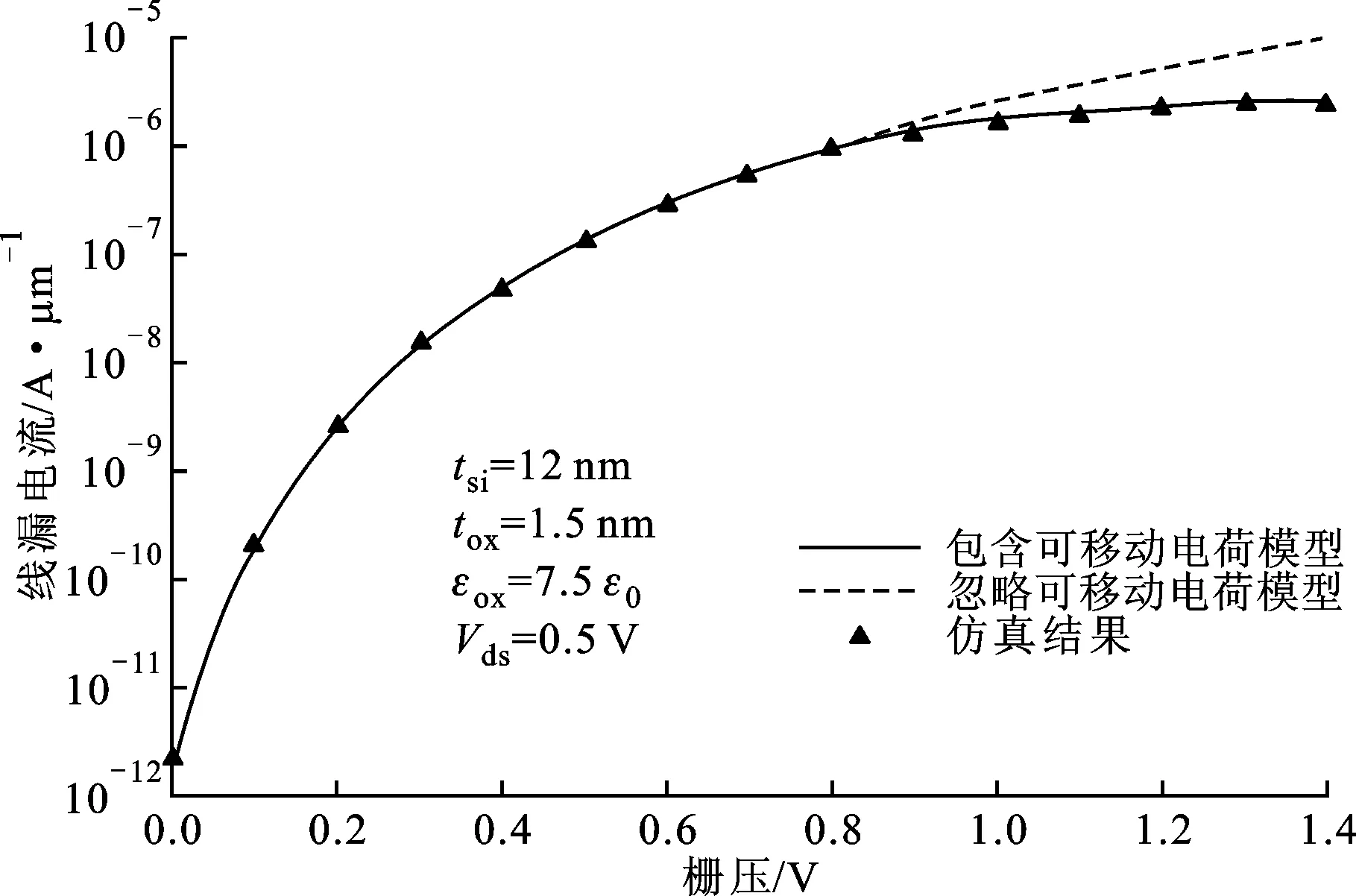
图4 2种模型下的转移特性曲线

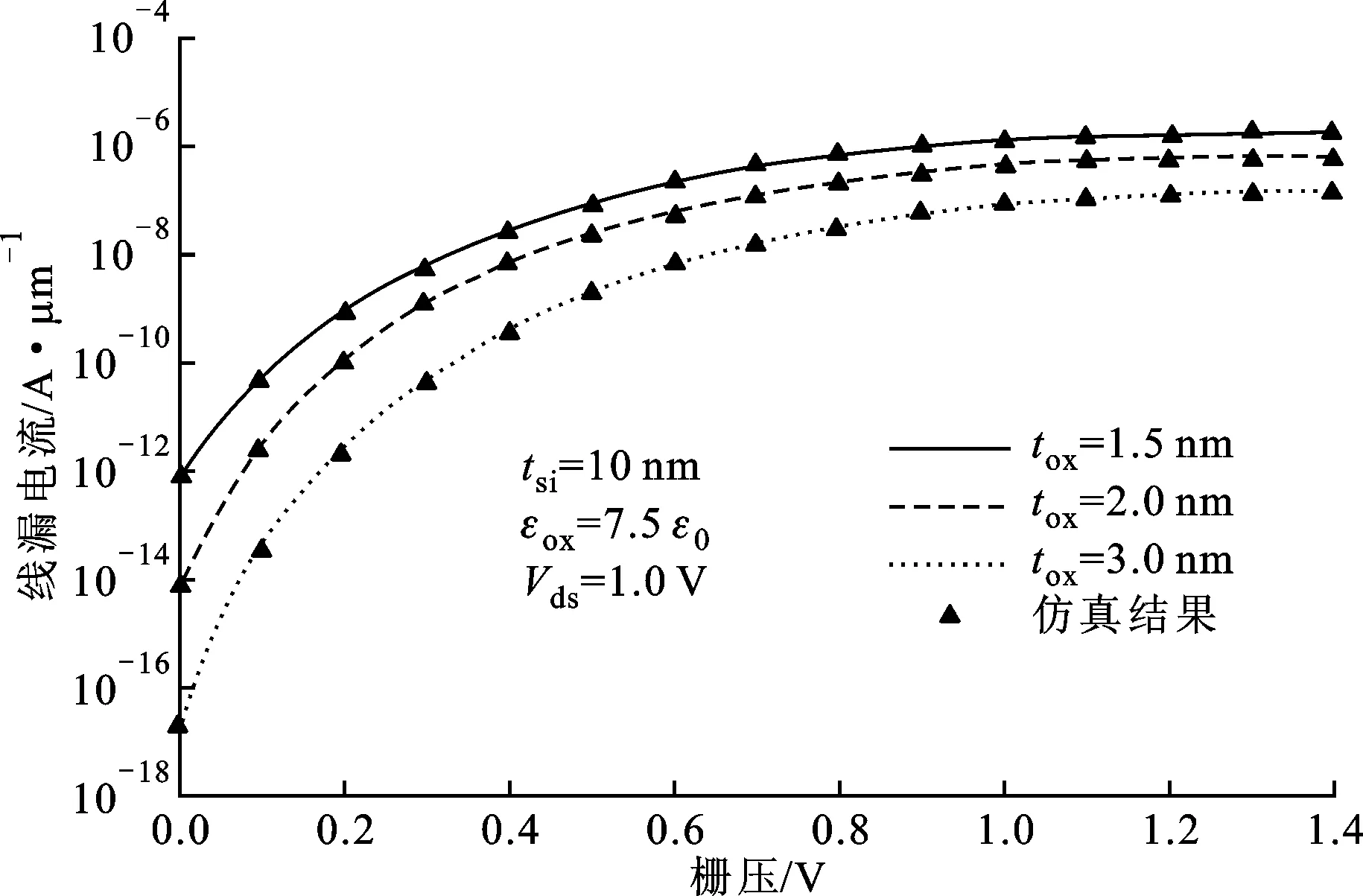
图5 不同栅氧化层厚度下的转移特性曲线

图5显示了不同栅氧化层厚度下的转移特性曲线。从图中可以观察到,减小氧化层厚度能够获得更大的漏电流。这是由于随着栅氧化层厚度的减小,栅压在栅绝缘层上的分压减小,在沟道中的分压增加,导致势垒区场强变大,漏电流增大。

图6显示了不同栅介质材料下的转移特性曲线。从图中可以观察到,栅介质的介电常数越高,漏电流越大。造成这种现象的原因是高介电常数的提高了栅和隧穿势垒的耦合能力,减小了隧穿势垒宽度,从而提高了线漏电流[26]。

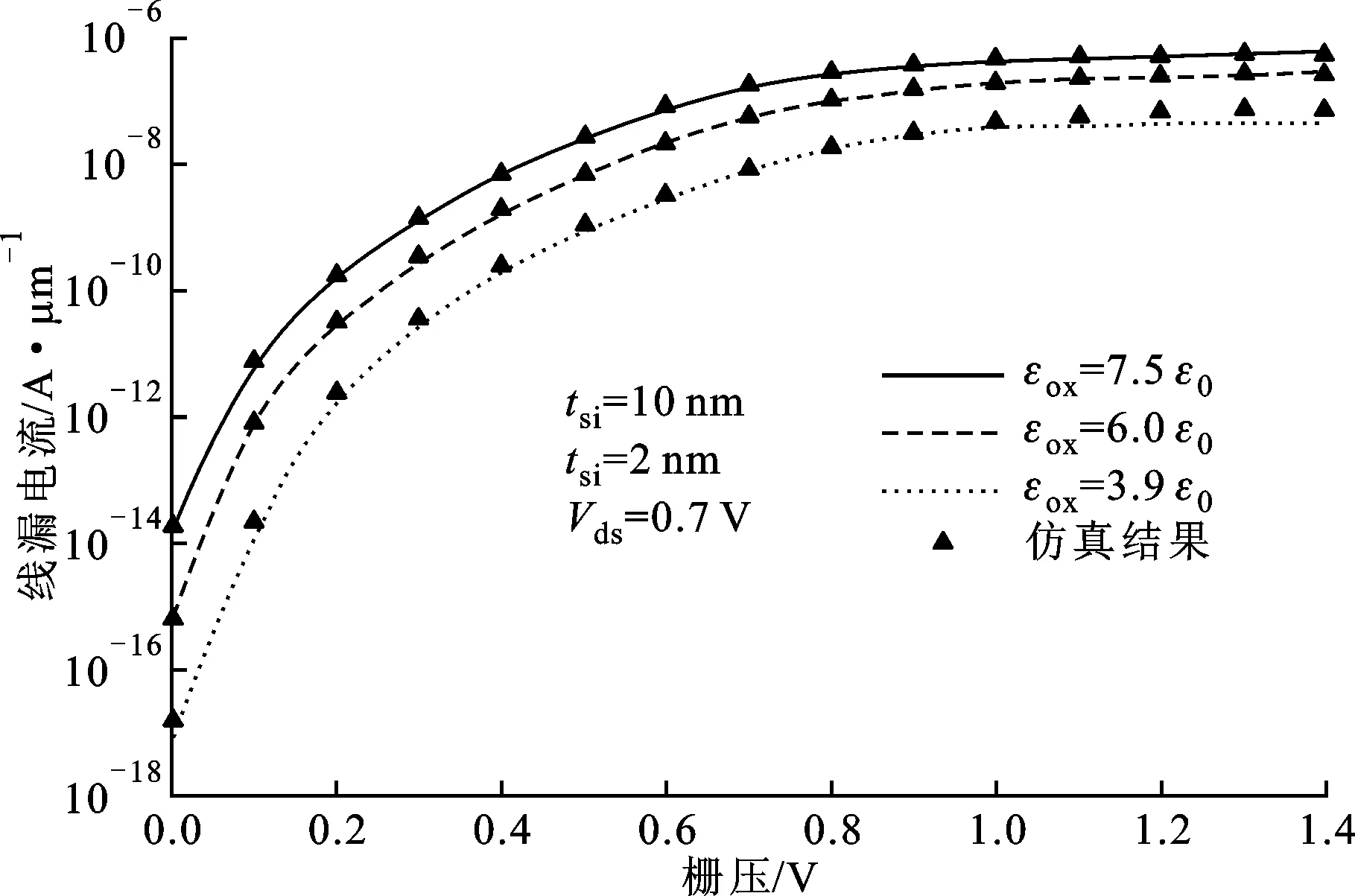
图6 不同栅介质介电常数下的转移特性曲线

图7显示了不同硅层厚度下的转移特性曲线。从图中可以观察到,更薄的硅层厚度能减小体电容效应,提高线漏电流。

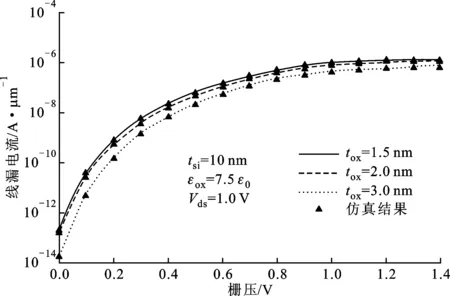
图7 不同硅层厚度下的转移特性特性曲线

由图3～图7可以得出结论:当栅压较高时,沟道进入强反型区,可移动电荷的影响不可忽略;本文所建立的考虑可移动电荷的解析模型从亚阈区到强反型区均与数值仿真结果吻合;可以通过采用更薄的氧化层厚度、高K栅介质材料和更薄的体硅厚度来提高漏电流。

3 结 论

本文在考虑可移动电荷效应的基础上建立了一种双栅TFET的漏电流简洁解析模型。通过电势迭代原理求解二维电势泊松方程,表面势电势、电场和载流子隧穿产生率的解析表达式,再用切线近似法计算隧穿产生率在隧穿区域的积分,得到漏电流的解析模型。用数值仿真软件对所建模型进行了验证,对比分析了不同器件参数条件下漏电流的转移特性,结果显示:从亚阈值区到强反型区所建模型均与仿真结果相吻合,精度提高了20%以上;在强反型区可移动电荷的影响已不可忽略。

[1] KOSWATTA S O, LUNDSTROM M S, NIKONOV D E. Performance comparison between p-i-n tunneling transistors and conventional MOSFETs [J]. IEEE Transactions on Electron Devices, 2009, 56(3): 456-465.

[2] CHOI W Y, PARK B G, LEE G D, et al. Tunneling field effect transistors (TFETs) with subthreshold swing(SS) less than 60 mV/dec [J]. IEEE Transactions on Electron Devices, 2007, 28(8): 743-745.

[3] 韩名君, 柯导明, 迟晓丽, 等. 超短沟道电势的二维半解析模型. [J]. 物理学报, 2013, 62(9): 1-7. HAN Mingjun, KE Daoming, CHI Xiaoli, et al. A two-dimensional semi-analytical potential model for ultra short channel. [J]. Journal of Physics, 2013, 62(9): 1-7.

[4] 甘学温, 王旭社, 张兴. 双栅和环栅MOSFET中短沟效应引起的阈值电压下降 [J]. 半导体学报, 2001, 22(12): 1581-1585. GAN Xuewen, WANG Xushe, ZHANG Xing. Threshold voltage dropping caused by the short channel effect in double-gate and surrounding-gate MOSFET. [J]. Journal of Semiconductors, 2001, 22(12): 1581-1585.

[5] 骆东旭, 李尊朝, 关云鹤, 等. 一种新型GaAs基无漏结隧穿场效应晶体管 [J]. 西安交通大学学报, 2016, 50(2): 68-72. LUO Dongxu, LI Zunchao, GUAN Yunhe, et al. A new type of GaAs base TFET without channel/drain junction. [J]. Journal of Xi’an Jiaotong University, 2016, 50(2): 68-72.

[6] VISHNOI R, KUMAR M J. An accurate compact analytical model for the drain current of a TFET from subthreshold to strong inversion [J]. IEEE Transactions on Electron Devices, 2015, 62(2): 478-484.

[7] BARDON M G, NEVES H P. Pseudo two dimensional model for double-gate tunnel FETs considering the junctions depletion regions [J]. IEEE Transactions on Electron Devices, 2010, 57(4): 827-834.

[8] PANDEY P, RAJAT V, KUMAR M J. A full range dual material gate tunnel field effect transistor drain current model considering both source and drain depletion region band-to-band tunneling [J]. Journal of Computational Electronics, 2015, 14: 280-287.

[9] SAMUEL T S A, BALAMURUGAN N B. An analytical modeling and simulation of dual material double gate tunnel field effect transistor for low power applications [J]. Journal of Electrical Engineering & Technology, 2014, 9(1): 247-253.

[10]WAN J, ROYER C L, ZASLAVSKY A, et al. A tunneling field effect transistor model combining interband tunneling with channel transport [J]. Journal of Applied Physics, 2011, 110(10): 104503.

[11]GHOLIZADEH M, HOSSEINI S E. A 2-D analytical model for double-gate tunnel FETs [J]. IEEE Transactions on Electron Devices, 2014, 61(5): 1494-1500.

[12]PAN A, CHEN S, CHUI C O. Electrostatic modeling and insights regarding multigate lateral tunneling transistors [J]. IEEE Transactions on Electron Devices, 2013, 60(9): 2712-2720.

[13]VERHULST A S, LEONELLI D, ROOYACKERS R, et al. Drain voltage dependent analytical model of tunnel field effect transistors [J]. Journal of Applied Physics, 2011, 110(2): 024510.

[14]VISHNOI R, KUMAR M J. A compact analytical model for the drain current of gate-all-around nanowire tunnel FET accurate from sub-threshold to on-state

[J]. IEEE Transactions on Electron Devices, 2015, 14(2): 358-362.

[15]韩忠方. 隧穿晶体管的模拟研究 [D]. 上海: 复旦大学, 2012.

[16]CHO E N, SHIN Y H, YUN L. Channel doping-dependent analytical model for symmetric double gate metal-oxide-semiconductor field-effect transistor: II Continuous drain current model from subthreshold to inversion region [J]. Journal of Applied Physics, 2013, 113(21): 214507.

[17]QIANG C, EVANS M H, JAMES D M. A physical short channel threshold voltage model for undoped symmetric double-gate MOSFETs [J]. IEEE Transactions on Electron Devices, 2003, 50(7): 1631-1637.

[18]TAUR Y, LIANG X, WANG W, et al. A continuous, analytic drain current model for DG MOSFETs [J]. IEEE Electron Device Letter, 2004, 25(2): 107-109.

[19]KANE E O. Theory of tunneling [J]. Journal of Applied Physics, 1961, 32(1): 83-91.

[20]HURKX G A M, KLAASSEN D B M, KNUVERS M P G. A new recombination model for device simulation including tunneling [J]. IEEE Transactions on Electron Devices, 1992, 39(2): 331-338.

[21]LI Zunchao, ZHANG Ruizhi, LIANG Feng, et al. Analytical and numerical study of the impact of HALOs on surrounding-gate MOSFETs [J]. IEICE Transactionson Electronics, 2009, 92(4): 558-563.

(编辑 刘杨)

Analytical Drain Current Model Considering Mobile Charges for Double-Gate Tunneling Field Effect Transistor

MENG Qingzhi,LI Zunchao,GUAN Yunhe,ZHANG Yefei

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

An analytical drain current model considering mobile charges for double-gate tunneling field effect transistor is proposed to solve the problem that the precision of surface potential and drain current of the tunneling field effect transistor (TFET) declines in strong inversion regions. Firstly, the 2-D potential Poisson’s equation is solved by taking the contribution of mobile charges into account to get the analytical expressions of the surface potential and the electric field. Then the electric field distribution and Kane model are used to get the generation rate of the carriers. Finally a compact analytical drain current model is derived by using the tangent line approximation method to calculate the integration of the tunneling generation rate in the tunneling region. The analytical model is verified by using the device numerical simulation software Sentaurus under different device parameters. Simulation results show that considering the mobile charges improves the precision of the drain current model in strong inversion regions. Comparisons with the models without considering the mobile charges show that the precision of the model considering the mobile charges is improved by more than 20%.

tunneling field effect transistor; mobile charges; surface potential; drain current; compact analytical model

10.7652/xjtuxb201608007

2016-01-17。 作者简介:孟庆之(1989—),男,硕士生;李尊朝(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61176038);陕西省工业科技攻关计划资助项目(2016GY-075)。

时间:2016-05-17

http:∥www.cnki.net/kcms/detail/61.1069.T.20160517.1736.006.html

TN386.6

A

0253-987X(2016)08-0038-07