多参量耦合的电主轴热特性建模及分析

康跃然,史晓军,高建民,李法敬

(西安交通大学机械制造系统工程国家重点实验室,710054,西安)



多参量耦合的电主轴热特性建模及分析

康跃然,史晓军,高建民,李法敬

(西安交通大学机械制造系统工程国家重点实验室,710054,西安)

为了深入研究电主轴热特性,通过分析轴承非线性力学特性与热效应间的耦合作用机制,建立了综合考虑热诱导预紧力和黏温效应的轴承动态生热计算模型;在引入接触热阻的基础上,基于系统内部多参量耦合关系,建立了电主轴热-结构耦合计算方法。以某型号电主轴为试验平台,进行了温升及热变形试验,利用试验数据对所建模型和分析方法进行了验证。最后,采用所建模型,对电主轴进行了热特性分析,结果表明:不同工况下电主轴仿真结果与试验数据吻合度良好,所建模型和分析方法进一步提高了仿真计算精度;电主轴温度场分布表现为外冷内热;轴芯热积聚导致的电主轴轴向热伸长是影响加工精度的主要因素;受到配合方式和装配位置的影响,轴承在温升过程中预紧力不断减小。

热诱导预紧力;黏温效应;热-结构耦合计算;热伸长

电主轴是现代高速、高精度数控机床的核心功能部件,其性能直接决定加工精度与效率。随着电主轴零部件设计、制造和装配等技术的不断进步,诸如几何装配、刀具磨损及伺服控制等引起的误差所占比例逐渐减小,而在高速、高精度极端加工条件下,电主轴热变形导致的加工误差则日益凸显。大量研究与生产实践表明,在高速、高精密加工中,热变形引起的误差占总误差高达60%～80%[1]。因此,建立精确的电主轴热特性分析模型,深入研究不同运行工况条件下电主轴的温升和热变形机理,对进一步发展电主轴技术无疑有着重要的理论意义和工程应用价值。

文献[2]借助有限元分析软件对电主轴进行了温度场的仿真模拟,通过试验验证了有限元方法分析电主轴热特性的可行性。文献[3]通过对转速为40 000 r/min的高速电主轴进行热分析及试验研究,获得了在不同转速下的温度场及热变形。文献[4]建立了一种考虑系统热响应和预紧方式影响的角接触球轴承热-机耦合动力学模型,分析了不同运行状态下主轴轴承的摩擦损耗及动态支承刚度。文献[5]通过构建电主轴瞬态热网络模型,获得了轴系温度场及热参数的瞬态变化特性,并结合试验验证了瞬态模型的准确性。

国内外学者对电主轴热特性分析模型进行了一定研究,但考虑电主轴温度场与热变形耦合机理的分析模型仍有待深入研究,以进一步提高模型准确性。为此,本文通过分析轴承非线性力学特性与热效应间的耦合作用机制,建立了轴承动态生热计算模型。在引入接触热阻模型的基础上,基于系统内部多参量耦合关系,建立了电主轴热-结构耦合计算方法,并通过试验数据与有限元计算结果分析对比,对所建模型和分析方法进行了验证。最后,采用所建模型对电主轴热特性进行了分析。

1 电主轴热特性建模

1.1 轴承动态生热计算模型

电主轴轴承摩擦生热受到轴承结构、外加负载和润滑油黏度等多个复杂因素共同影响,在系统达到热平衡之前,各因素间是动态耦合相互作用的。基于Palmgren整体生热模型,将轴承摩擦力矩分为内、外圈分量Mij、Moj[6]

(1)

式中:Z为轴承滚动体个数;Db为滚动体直径;di、do分别为内、外圈滚道与滚动体接触点处的直径;dm为轴承节圆直径;n为轴承转速;f0为与轴承类型和润滑方式有关的系数;ν是润滑油的运动黏度;P1i、P1o为轴承内、外圈摩擦力矩的计算负荷;f1为与轴承类型和所受负载有关的系数。

由于润滑油本身的黏温效应,其对轴承生热的影响如图1所示,随着润滑油温度升高,其运动黏度逐渐降低,进而导致轴承生热量不断减少。以轴承常用的32#机油为例,其不同温度下的运动黏度可表示为

(2)

式中:T为润滑油温度。

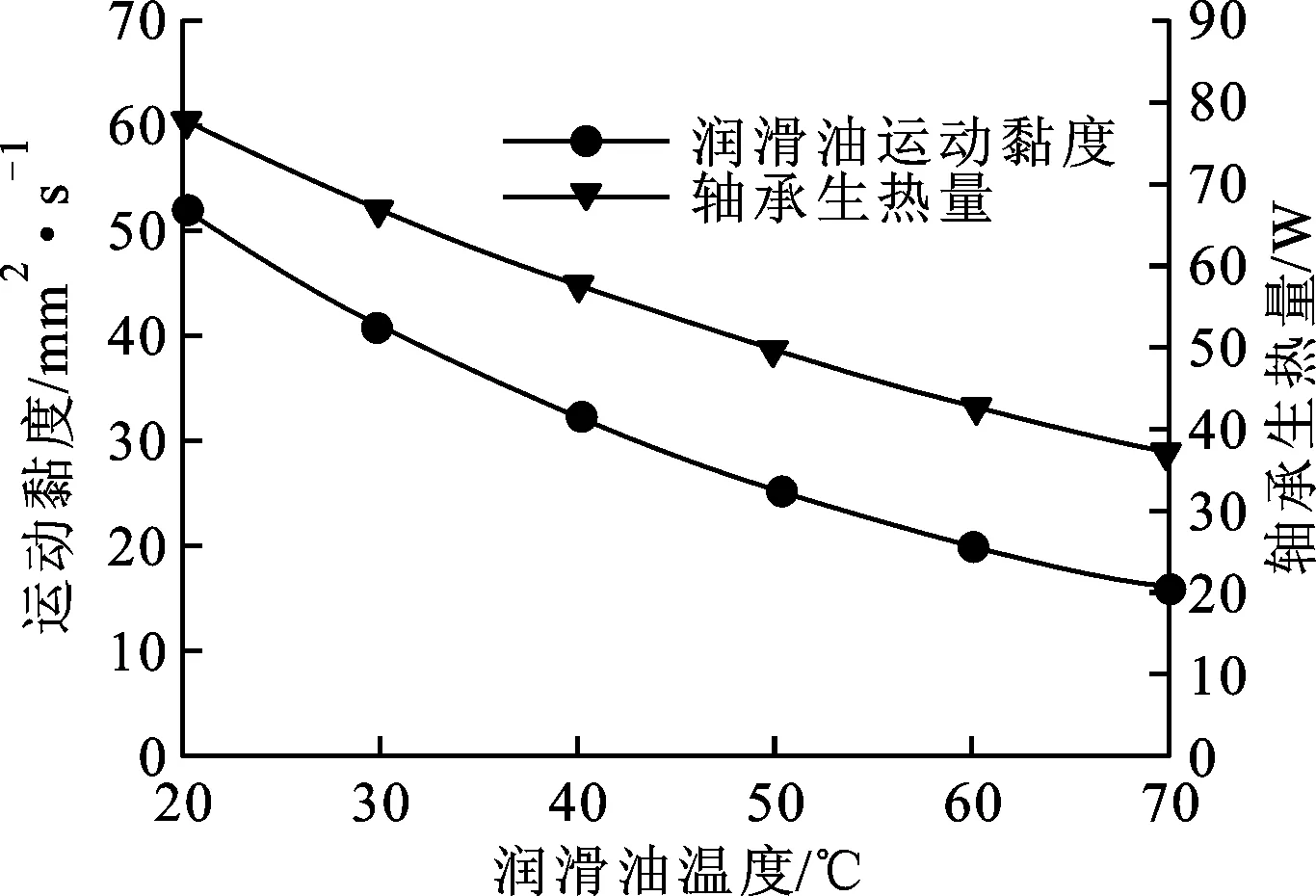
图1 润滑油黏温效应对轴承生热的影响

此外,P1i、P1o和f1均与轴承负载受力有关,以f1为例

(3)

式中:C0为轴承基本额定静载荷;P0为轴承当量静载荷,可由下式获得

P0=0.5Fa+0.46Fr

(4)

其中Fa、Fr分别为轴承的轴向及径向载荷,它们需要根据轴承不同的配置形式做具体的分析计算,如表1所示。

轴承组承受总载荷表达式为

(5)

式中:α为轴承实际接触角;m为轴承个数。

对于采用定位预紧的轴承,其温升过程中的热变形会造成轴承内、外圈相对几何关系的改变,由此产生的热诱导预紧力,反过来会进一步影响电主轴热特性。忽略轴承径向和滚动体变形以及由于离心力带来的轴承内、外接触角不相等,假设轴承只发生刚体位移和局部弹性变形,可建立如下模型。

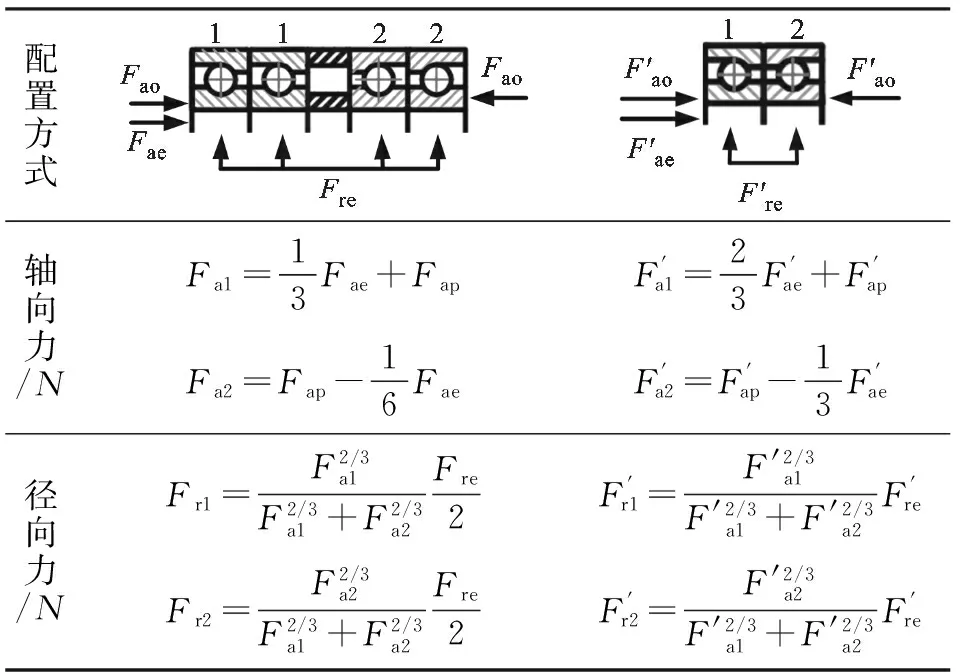
表1 轴承组受力分析

注:Fao为轴承运行过程中的实际预紧力;Fae、Fre分别为轴承组承受的轴向及径向载荷;Fap为轴承组承受的总载荷。

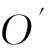
(6)

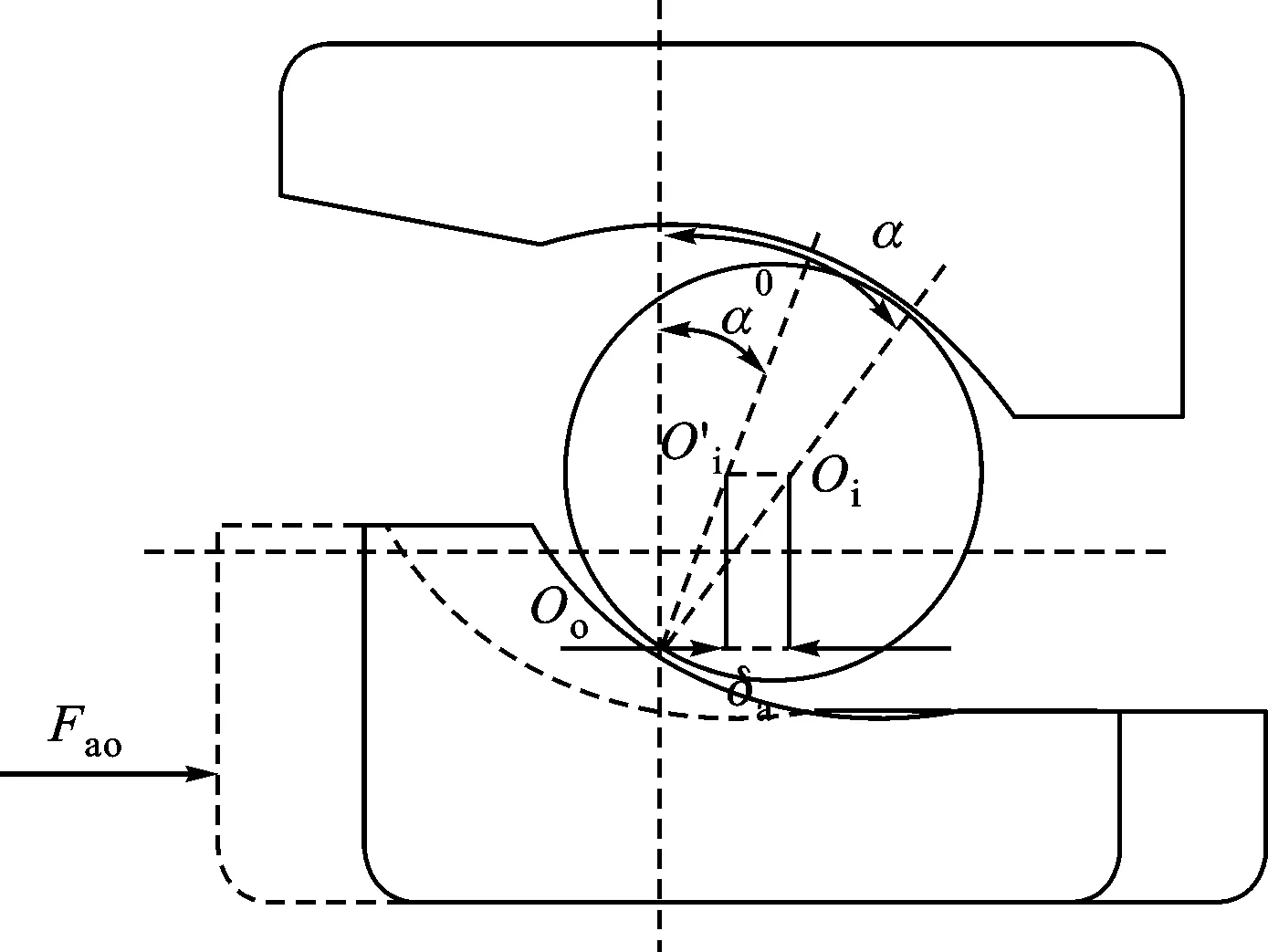
图2 轴承接触角变化

参考轴承内部载荷计算理论,通过轴向位移与接触角的关系式,采用Newton-Raphson法进行迭代,求解出轴承轴向位移δa与实际变形后轴承接触角α的关系式[7]

(7)

式中:B为总曲率。将求得的接触角α代入式(8),可求得轴承热变形后的实际预紧力

(8)

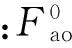
轴承在运转时,滚动体受到外滚道控制,滚动体与内圈之间存在自旋摩擦力矩[4]

(9)

式中:μSi为滚动体与内圈滚道的滑动摩擦因数;aij为滚动体与内圈滚道的赫兹接触椭圆长半轴;L(K)ij为滚动体与内圈滚道赫兹接触椭圆的第二类完全积分。

由此可获得单个滚动体与轴承内、外圈接触区的摩擦生热为

(10)

式中:ωsij为滚动体的自旋角速度。

进一步根据Burton的理论[8],忽略保持架和导引套圈对热的影响,将上述轴承摩擦生热量按1∶1的比例平均分配到滚动体和与其接触的内、外圈接触滚道上，从而有

(11)

式中:Hi、Ho分别为轴承内、外圈滚道表面生热;Hb为滚动体表面生热。

1.2 电主轴内部接触热阻

电主轴各零部件在微观上并未完全接触,存在着一定的空隙,由此产生的接触热阻会使通过的热流产生一部分损失,进而影响电主轴温度场分布及热变形结果。通过在关键部位建立接触热阻计算模型可进一步提高所建模型精度。

(1)轴承滚动体与内外圈接触热阻R由接触面的形状和大小决定[9]

(12)

式中:ψ为与接触面大小有关的几何参数;λ1、λ2分别为轴承内、外圈和滚动体的热导率;a为轴承赫兹椭圆接触区域的长半轴。

(2)轴承内圈与轴芯是过盈配合,其热传导率hs与零件及介质热导率、结合面加工参数有关

(13)

式中:Lg为未接触空间厚度;A为名义接触面积;Ac为实际接触面积;Av为未接触部分的面积;λa及λf分别为轴芯热导率和空隙间介质的热导率。A、Ac、Av均需根据接触理论,综合考虑粗糙表面的微观形貌与微凸体变形来求解获得[10]。

(3)轴承外圈由于与轴承座采用间隙配合,其热传导率与轴承几何结构、配合方式及材料物性参数等因素有关

(14)

式中:hring为轴承外圈的厚度;hgap为轴承外圈与轴承座的平均间隙;λair为空气的热导率。

1.3 电主轴热-结构耦合计算方法

电主轴在达到热平衡前,系统内部多参量间相互耦合,且各参量是随温度、时间变化的非线性函数。基于上述计算模型,通过有限元仿真软件Ansys与Matlab的交互协同,建立电主轴热-结构耦合计算方法,其算法流程如图3所示。

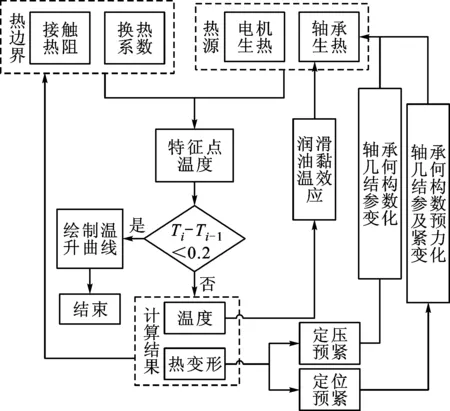
图3 电主轴热-结构耦合计算方法流程图

电主轴热-结构耦合算法的思路为:基于上文所建轴承生热及接触热阻计算模型,以及电主轴内置异步电机热损耗[11]和散热边界条件进行计算[12],获得初始热源及热边界的解析值,然后加载至有限元模型;按一定规律设置电主轴瞬态温升过程中的时间节点,先通过有限元分析求得第一个时间节点的温度场分布和内、外圈的相对热变形,进而在Matlab中对换热系数、润滑液黏度、预紧力及接触热阻等热参量进行修正;然后,将修正后的热参量作为下一个时间节点的热源及边界条件,加载至有限元分析模型上进行下一个时间节点的仿真计算;如此迭代计算,直到系统某一时刻的特征温度与上一时刻的差值小于0.2 ℃,即可认定系统达到热平衡。

2 电主轴热特性模型验证

在建立的电主轴试验平台上,测量某型号磨削电主轴在不同转速工况条件下的温升和轴端热变形[13],利用试验数据对所建模型和分析方法进行验证。该电主轴额定功率为12.4 kW,最高转速为24 000 r/min,其内置电机为三相异步交流电机,轴承串联配置,前轴承B7008定位预紧,后轴承B7007定压预紧,油雾润滑。在电主轴前轴承1外圈布置pt100型温度传感器(见图4),该传感器精度为A级、误差为(0.15±0.000 2|t|) ℃,通过预紧弹簧保证其与目标测试面的紧密接触,保证测温迅速准确。试验时采集仪实时记录轴承温升数据,直到系统达到热平衡为止。在轴芯前端加装电涡流位移传感器来测量轴端面的热变形(见图5)。试验前依据被测面材料特性对传感器进行标定。由于被测端面存在一定的跳动量,所以需要对试验数据进行高频滤波处理,保留低频下随温升变化的热变形量,以保证试验数据测量精度。

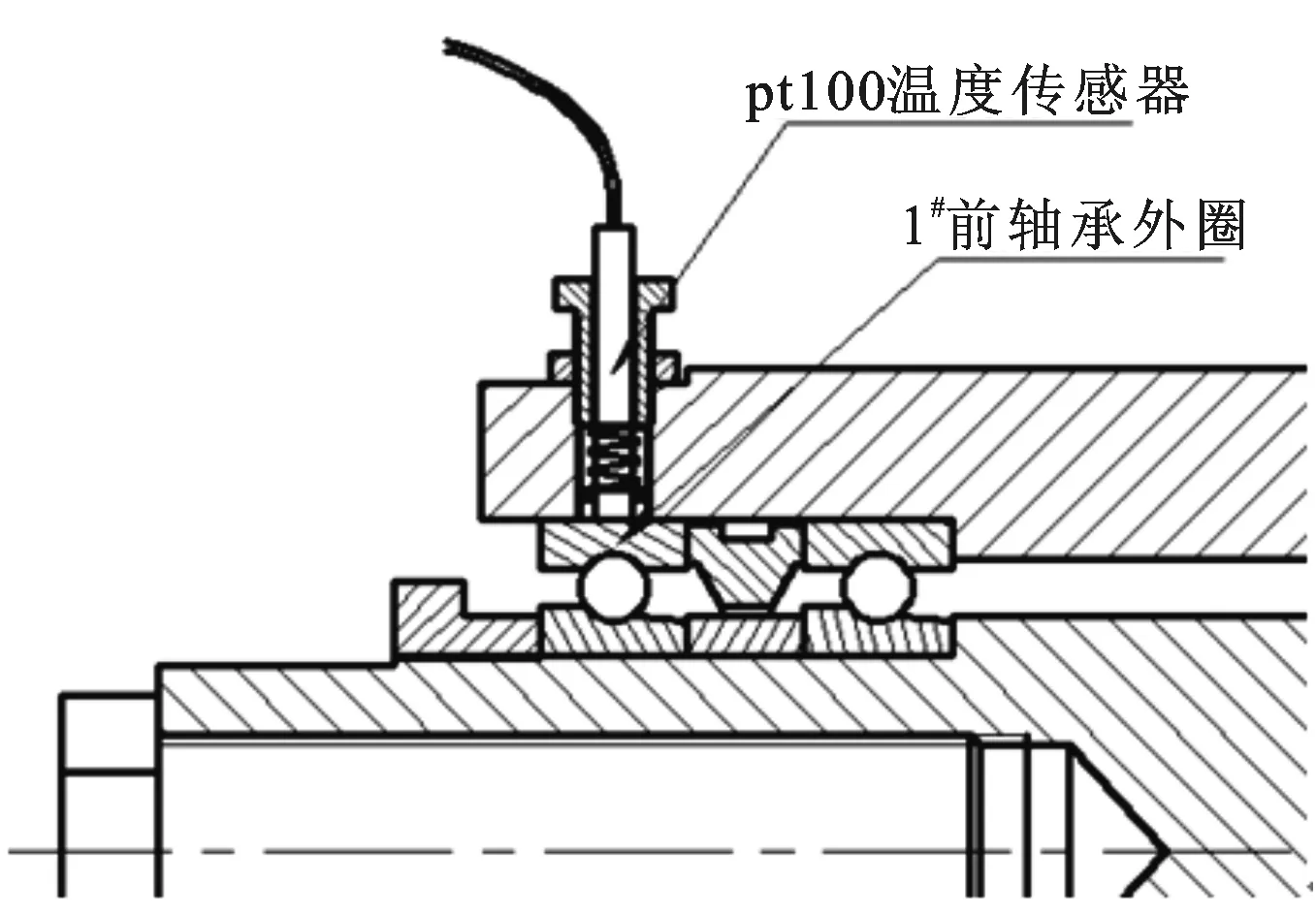
图4 轴承温度传感器布置

图5 轴端热变形测量装置

试验工况如下:定子冷却水套流量为16 L/min,环境温度为23 ℃,系统轴端空载,轴承中度预紧力为300 N,油雾润滑流量为10 L/s。共设定6 000、8 000、10 000、12 000、15 000 r/min 5组不同转速工况。每组试验结束后,确保将电主轴系统冷却至室温,再进行下一组试验。

针对目标对象特征,建立三维简化几何模型,如图6所示。在有限元仿真中,将采用定压预紧方式的轴承外圈与轴承座内圈结合面设为摩擦接触类型,轴承内、外圈与滚动体接触设置为不分离状态,对于采用螺钉连接的结合面,算法设置为MPC。基于上文所建模型,采用热-结构耦合计算方法对电主轴进行有限元分析。

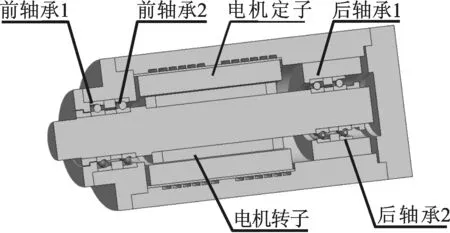
图6 电主轴简化模型

图7为电主轴不同转速下轴承外圈瞬态温升的计算结果和试验数据对比,可见两者温升趋势吻合较好。表2为所建模型与文献[14]模型的计算误差对比,本文所建模型将稳态时温升最大误差由15.5%减小为6.4%。

图7 不同转速下轴系瞬态温升仿真与试验对比

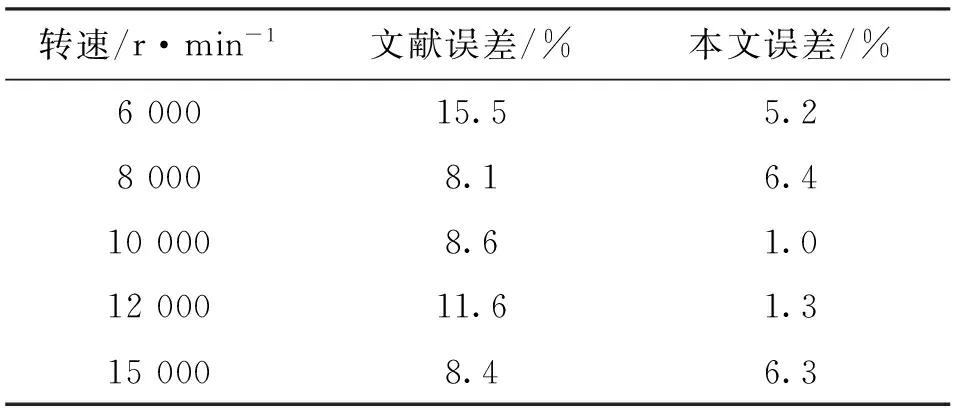
转速/r·min-1文献误差/%本文误差/%600015.55.280008.16.4100008.61.01200011.61.3150008.46.3

图8为不同转速工况下电主轴轴端热变形的计算和试验结果对比。由图可见,随着转速增加,电主轴轴端热变形不断增大,不同工况下试验与仿真数据最大误差为7.8%,与文献[14]中的模型相比,本文所建模型的计算精度有了进一步的提升。

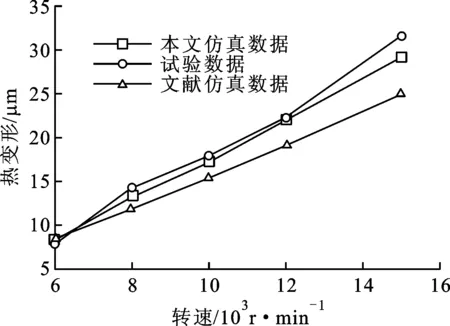
图8 两种模型电主轴热变形仿真与试验结果对比

3 电主轴热特性分析

3.1 电主轴稳态温度场

采用所建模型和方法,分析了该电主轴在特定工况条件(转速为10 000 r/min,空载)下的温度场分布,如图9所示。系统电机转子处的温度最高为63.42 ℃,其次是前、后轴承,而壳体部分由于靠近冷却水套温升最低,在7 ℃左右。由于冷却水套只能作用于相邻部分的电机定子和壳体,无法实现系统内部,特别是轴芯处积聚热的快速引出和高效冷却,从而使整个电主轴形成了外冷内热的温度分布格局。由于存在接触热阻,轴承外圈与轴承座间出现了明显的温度分布不连续。

图9 电主轴内部温度场

3.2 电主轴热变形

将上文求解获得的系统温度场结果作为体载荷导入静力学分析中。在零件螺栓连接面和轴承定位处施加位移约束,对整个系统施加重力场,求解获得电主轴热变形,结果如图10、图11所示。

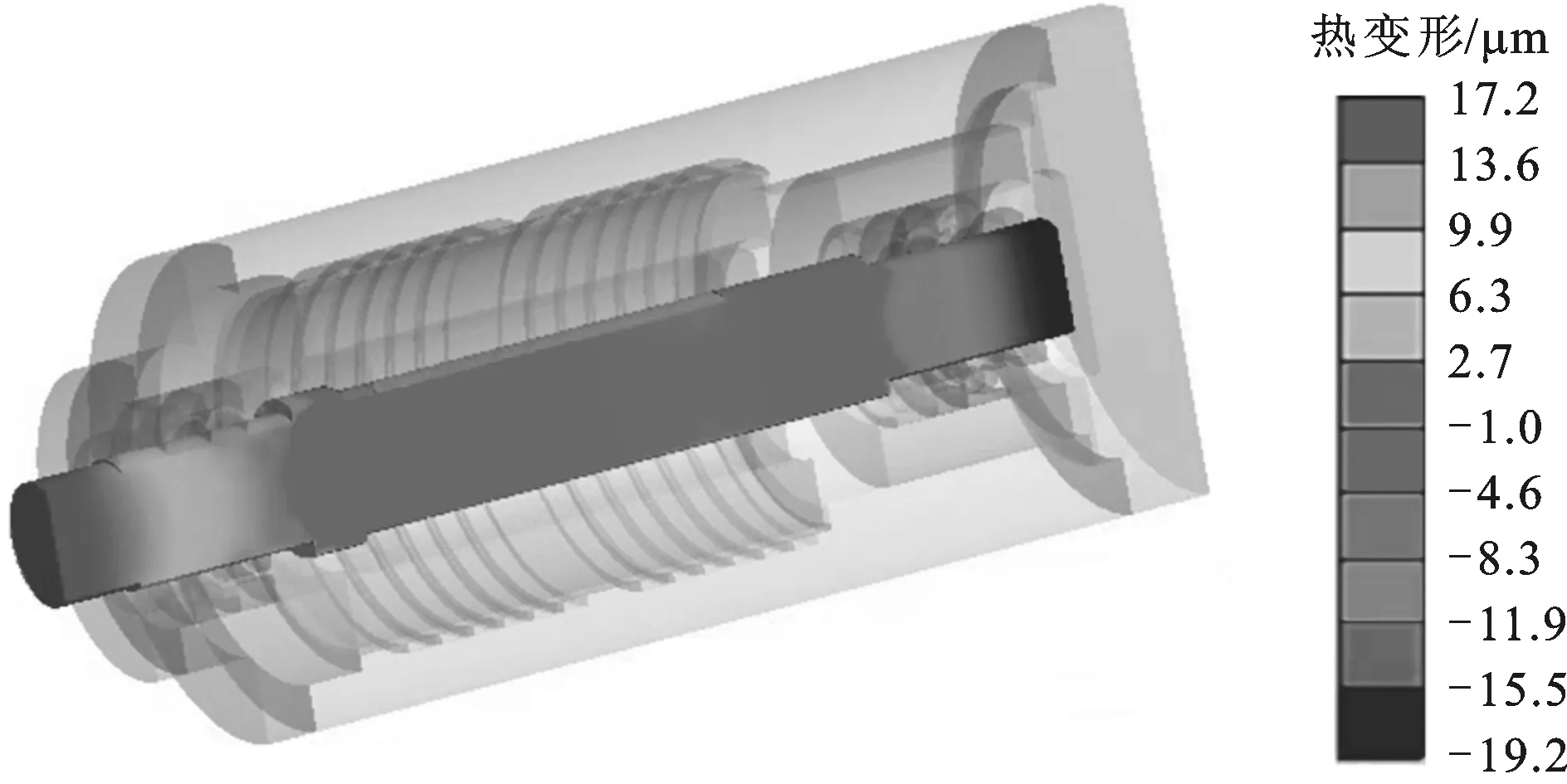
图10 电主轴轴芯轴向热变形

图11 电主轴径向热变形

在热稳态条件下,电主轴轴芯两端轴向热变形较大,后端热伸长最大达19.2 μm,虽然热特性分析显示该区域的温升并不是最大的,但由于轴芯热积聚,使其轴向方向温度梯度变化较大(最大温差达23 ℃左右),再加之各零部件间的配合关系进一步限制了轴向方向的自由度,热变形逐渐累积叠加至前、后端。电主轴径向热变形最大为15.6 μm,由于系统本身的热对称设计,变形沿中轴线对称分布,对加工精度影响相对较小。

3.3 电主轴瞬态热特性分析

图12为电主轴各典型区域最高温度随时间的变化情况。在系统运行初始阶段,各区域温度急速上升,而由于彼此热环境的差异,各部分温升速率不同。待系统稳定运行一段时间后,在油雾、冷却水套等装置连续、有效的运行作用下,系统生热与换热之间趋于平衡,最终达到热稳态。

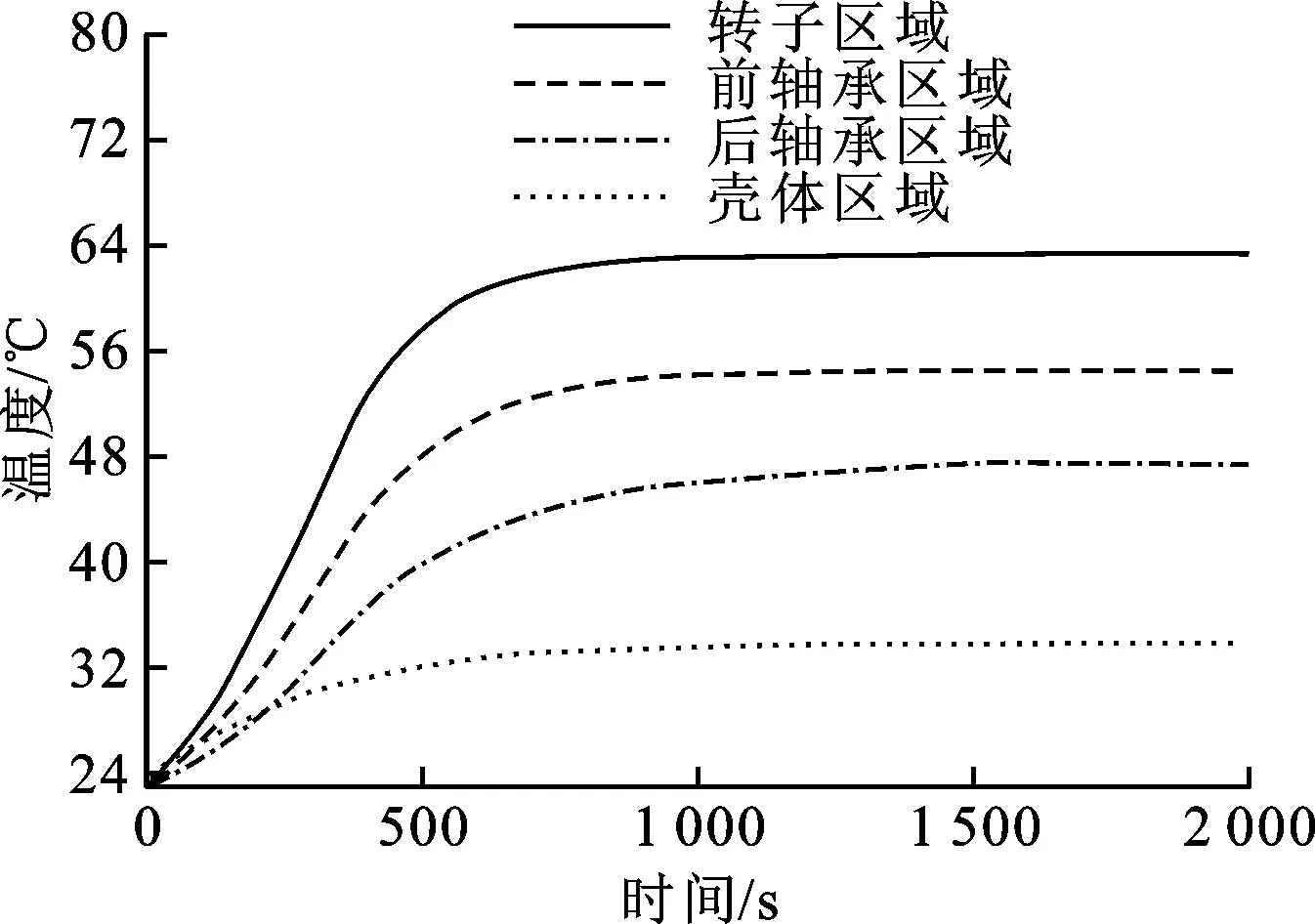
图12 电主轴各区域温度变化

前轴承预紧力随时间的变化如图13所示。在电主轴运行初期,对于采用串联配置的前轴承,由于仅考虑内、外圈的相对轴向热位移,且其变化方向与轴承初始预紧方向相反,产生的热诱导预紧力使轴承预紧力急剧减小,前轴承2由于装配位置临近电机,温升及预紧力变化较大,而随着系统逐渐达到热稳态,轴承预紧力的变化也趋于平缓。

图13 轴承预紧力随时间变化

4 结 论

(1)建立了综合考虑热诱导预紧力和黏温效应的轴承动态生热计算模型,在引入接触热阻计算模型的基础上,基于系统内部多参量耦合关系,建立了电主轴热-结构耦合计算方法。

(2)有限元计算结果与试验数据对比显示:不同转速工况下,两者瞬态温升趋势一致;热稳态时轴承外圈温升偏差最大为6.4%,轴向热变形误差最大为7.8%,所建模型的计算精度进一步提高。

(3)采用所建模型和计算方法,对电主轴进行了热特性分析。结果表明:电主轴表现外冷内热的温度分布;轴芯热积聚导致的电主轴轴向热伸长是影响加工精度的主要因素;受到配合方式和装配位置的影响,轴承在温升过程中预紧力不断减小。

[1] OKAFOR A C, YALCIN M. Derivation of machine tool error models and error compensation procedure for three axes vertical machining center using rigid body kinematics [J]. International Journal of Machine Tools & Manufacture, 2000, 40(8): 1199-1213.

[2] JIN K C, DAI G L. Thermal characteristics of the spindle bearing system with a gear located on the bearing span [J]. International Journal of Machine Tools & Manufacture, 1998,38(9): 1017-1030.

[3] JIAN L, DONG H K. A study on the thermal characteristics and experiments of high-speed spindle for machine tools [J]. International Journal of Precision Engineering and Manufacturing, 2015, 16(2): 293-299.

[4] 陈小安, 刘俊峰, 合烨, 等. 高速电主轴热态性能及其影响 [J]. 机械工程学报, 2013, 49(11): 135-142. CHEN Xiao’an, LIU Junfeng, HE Ye, et al. Thermal properties of high speed motorized spindle and their effects [J]. Journal of Mechanical Engineering, 2013, 49(11): 135-142.

[5] 米维, 闫柯, 吴文武, 等. 考虑热-变形耦合的主轴-轴承系统瞬态热特性分析 [J]. 西安交通大学学报, 2015, 49(8): 52-57. MI Wei, YAN Ke, Wu Wenwu, et al. Transient thermal property analysis for spindle-bearing system considering thermo-deformation coupling [J]. Journal of Xi’an Jiaotong University, 2015, 49(8): 52-57.

[6] 康辉民, 陈小安, 陈文曲, 等. 高速电主轴轴承热分析与实验研究 [J]. 机械强度, 2011, 33(6): 797-802.

KANG Huimin, CHEN Xiao’an, CHEN Wenqu, et al. High speed motorized spindle bearing thermal analysis and experimental research [J]. Journal of Mechanical Strength, 2011, 33(6): 797-802.

[7] HARRIS T A, KOTZALAS M N. 轴承技术的基本概念 [M]. 罗继伟, 马伟, 等译. 北京: 机械工业出版社, 2010: 138-140.

[8] BURTON R A, STAPH H E. Thermally activated seizure of angular contact bearing [J]. ASLE Trans, 1967, 10(4): 408-417.

[9] BERND B, JAY F. A thermal model for high speed motorized spindles [J]. International Journal of Machine Tools & Manufacture, 1999, 39(9): 1345-1366.

[10]刘志峰, 马澄宇, 赵永胜, 等. 基于接触热阻的高速精密电主轴热特性分析 [J]. 北京工业大学学报, 2016, 42(1): 17-23. LIU Zhifeng, MA Chengyu, ZHAO Yongsheng, et al. Analysis of high speed motorized spindle thermal characteristics based on thermal contact resistance [J]. Journal of Beijing University of Technology, 2016, 42(1): 17-23.

[11]BOSSMANNS B, TU J F. A power flow model for high speed motorized spindles: heat generation characterization [J]. Journal of Manufacturing Science and Engineering, 2001, 123(3): 494-505.

[12]MA Chi, YANG Jun, ZHAO Liang, et al. Simulation and experimental study on the thermally induced deformations of high-speed spindle system [J]. Applied Thermal Engineering, 2015, 86: 251-268.

[13]王梦茜. 机床电主轴热特性分析技术研究 [D]. 西安: 西安交通大学, 2014.

[14]WANG Mengxi, HONG Jun, WU Wenwu, et al. An improved model of motorized spindle for transient thermo-structural analysis [C]∥IEEE International Symposium on Assembly and Manufacturing. Piscataway, NJ, USA: IEEE, 2013: 91-96.

(编辑 杜秀杰)

Modeling and Analyzing Multi-Variable Coupling Therma Characteristics for Motorized Spindle

KANG Yueran,SHI Xiaojun,GAO Jianmin,LI Fajing

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710054, China)

Considering the coupling behaviors between the non-linear mechanics character and the thermal effect, a dynamic heat calculation model for rolling bearings taking heat-induced preload and temperature-viscosity effect into account is established. A thermo-structural coupling calculation method introducing the thermal contact resistance is developed according to the coupling parameters in the motorized spindle system. The temperature rising and thermal deformation tests are carried out to verify the accuracy of this model and algorithm, and the thermal characteristics of the motorized spindle are analyzed. It is found that the simulation results coincide well with the experimental data under different working conditions to indicate the effect of the proposed model on improving simulation precision. The temperature field distribution of the spindle trends high inside and low outside. The thermal expansion of spindle caused by the heat accumulation of shaft mainly affects the manufacturing accuracy. During the temperature rising process, the preload of bearings decreases due to the fitting manner and the assembly position.

heat-induced preload; temperature-viscosity effect; thermo-structural coupling calculation; thermal expansion

10.7652/xjtuxb201608006

2016-03-06。 作者简介:康跃然(1991—),男,硕士生;史晓军(通信作者),男,副教授。 基金项目:国家机床重大专项资助项目(2014ZX04001191)。

时间:2016-05-17

http:∥www.cnki.net/kcms/detail/61.1069.T.20160517.1902.012.html

TH113

A

0253-987X(2016)08-0032-06