对称离散事件系统状态树结构模型的控制函数不变性研究

焦亭,甘永梅,肖国春

(西安交通大学电气工程学院,710049,西安)



对称离散事件系统状态树结构模型的控制函数不变性研究

焦亭,甘永梅,肖国春

(西安交通大学电气工程学院,710049,西安)

针对对称离散事件系统中使用监督控制理论计算得到的自动机形式的监督控制器状态数较多且无法清晰反映控制逻辑等问题,提出了基于状态树结构的抽象控制函数计算方法。该方法通过充分利用系统的对称性,对避免缓冲区出现上溢或者下溢的性能指标,采用事件重标记映射提取各组中处于加工完成状态的组件数目,从而省去了各组件复杂的运行细节;然后利用状态树结构计算得到基于抽象状态信息的控制函数;最后,结合各组组件并行工作与串行工作的实例,分析所得控制函数的不变性,即在缓冲区容量固定的前提下,控制函数所需的状态信息与组件总数量无关。实验结果表明:在实际应用中借助控制函数的不变性可在结构相同的组件增减时免于重复计算控制函数;各组中重标记为同一事件的各可控事件可由同一控制函数进行使能,有效减少了控制函数的个数;相比于自动机形式的监督控制器,控制函数状态数更少且能更清晰地描述控制逻辑。

离散事件系统;监督控制理论;状态树结构;控制函数;谓词逻辑

在由Ramadge与Wonham建立的离散事件系统监督控制理论[1-2]中,由多组具有相同结构组件组成的系统具有对称性。对于不关注各组件之间性能指标差异的系统,可利用离散事件系统的对称性对系统进行化简。文献[3]利用群理论描述具有相同结构组件串联所构成系统的对称性,以达到简化控制器的目的。文献[4]对由具有相同结构组件组成的系统执行商自动机构建运算,以简化集中监督控制器规模。对于由同一模板生成的系统,文献[5]分析了系统的死锁与阻塞问题,文献[6]提出了基于广播方式且满足交换律、结合律的系统合成运算算法。这些化简方法均基于商自动机构建算法,计算过程复杂,本文提出通过事件重标记映射提取系统的抽象状态信息以简化系统。事件重标记映射不但能在很大程度上缩减被控对象与监督控制器规模,而且化简的实现过程更加直观简便,且所得的重标记后的监督控制器能直接用于控制。

在利用事件重标记映射提取系统的抽象状态信息后,基于所得的抽象状态信息建立状态树结构模型[7-10],计算得到系统中各可控事件的控制函数。此外,文献[11]通过证明使用supreduce算法计算所得控制同余(control congruence)的不变性以证明控制器的不变性,但此证明过程较为繁琐,而状态树结构中控制函数清晰的控制逻辑使得控制函数的不变性证明变得直观简便。

文献[12-14]中的性能指标主要是参数化模板或谓词表达式,本文主要研究在缓冲区容量固定的前提下防止缓冲区上溢与下溢的性能指标。在缓冲区容量固定的情况下,借助状态树结构计算系统中可控事件的控制函数,可发现控制函数具有不变性,即控制函数不随组件数目的增减而变化。

1 基础知识

1.1 DES自动机模型

离散事件系统利用自动机对系统进行建模,自动机可表示为5元组G=(Q,Σ,δ,q0,Qm),其中Q为状态集合,Σ为事件集合,δ:Q×Σ→Q用于描述系统中状态的变迁关系,q0为初始状态,Qm⊆Q为标识状态集合。一般地,转移函数可扩展为δ:Q×Σ*→Q,其中Σ*表示空字符串ε与Σ上的所有有限长度字符串的并集,并用δ(q0,s)!表示δ(q0,s)有定义。定义自动机G所表示语言的闭特性为L(G)={s∈Σ*|δ(q0,s)!},标识特性为Lm(G)={s∈Σ*|δ(q0,s)∈Qm}。

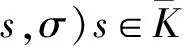
对于G的监督控制可定义为映射V:L(G)→Γ,其中所有控制模式组成的集合Γ记作Γ={γ∈Pwr(Σ)|γ⊇Σu}。G在V的监控下可记作V/G,并用L(V/G)表示V/G的闭特性[1]。令M⊆Lm(G),定义(M,G)的标识非阻塞监督控制为映射V:L(G)→Γ,V/G的标识特性定义为Lm(V/G)=L(V/G)∩M。假设用E⊆Σ*表示性能指标,E中的所有可控语言表示为C(E)={K⊆E|K关于G可控}。因C(E)中的元素形成上晶格结构,存在最大元素supC(E)=∪{K|K∈C(E)},并可由TCT软件中的supcon算法计算得到对应自动机形式的监督控制器。

1.2 状态树结构

对DES进行建模的状态树结构[8-9]可表示为6元组Gst=(St,H,Σ,Δ,St0,Stm),其中状态树St将系统状态集合表示为分层结构,H为被控系统Gst中描述系统局部行为的各组件实时子整体,Σ为事件集合,其被划分为可控事件集合Σc与不可控事件集合Σu。令S(St)表示St上所有的子状态树集合,Δ:S(St)×Σ→S(St)为全局转移函数,St0∈S(St)为初始状态树,Stm⊆S(St)为标识状态树集合。

B(St)⊆S(St)表示所有基本状态树集合,定义B(St)上的谓词P:B(St)→{0,1},其中0、1分别表示逻辑假、逻辑真。谓词P可由基本状态树集合BP:={b∈B(St)|P(b)=1}判定,其中P(b)=1常被记作bP。对于子状态树T∈S(St)定义TP当且仅当(∀b∈B(T))bP,状态树Gst也可记作Gst=(St,H,Σ,Δ,P0,Pm),其中P0、Pm为初始谓词、标识谓词。

定义P(St)为B(St)上的谓词集合。引入偏序关系,使得PP′,当且仅当(P)∨P′,对任意b∈B(St),如果bP⟹bP′,则PP′。可达谓词、协同可达谓词可分别记作R(Gst,P)、Cr(Gst,P),如果R(Gst,P)Cr(Gst,P),则称谓词P关于Gst非阻塞。

对任意σ∈Σ定义映射Mσ(P):P(St)→P(St)来表示bMσ(P),当且仅当Δ(b,σ)P。如果P满足(∀σ∈Σu)PMσ(P),则称谓词P弱可控。将谓词P所有非阻塞且弱可控的子谓词记作NC(P),由于NC(P)非空且在任意并运算∨作用下封闭,故存在最大元素supNC(P):=∨{K|K∈NC(P)}。定义状态反馈控制f:B(St)→Π,Π:={Σ′⊆Σ|Σu⊆Σ′},对任意事件σ∈Σ定义控制函数fσ:B(St)→{0,1},fσ(b)=1当且仅当σ∈f(b),控制函数f可由集合{fσ|σ∈Σ}表示。由定义可知,对于所有不可控事件σ,fσ(b)=1。状态反馈控制f可由控制函数fσ:=Mσ(supNC(P))表示,对任意b∈B(St),fσ(b)=1,当且仅当Δ(b,σ)supNC(P)。控制函数可由STSLib软件计算得到[8]。

1.3 事件重标记映射

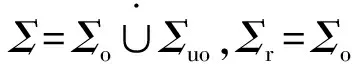
事件重标记映射R的示意图如图1所示,φ的结果代表自动机对应的语言。使用TCT中改进后的relabel算法,用λ表示,计算进行事件重标记后所得的自动机GR=λ(G),使其满足Lm(GR)=R(Lm(G)),L(GR)=R(L(G))。

图1 重标记映射及实现过程示意图

事件重标记算法λ主要分2步实现:将G中所有不可观测事件重标记为空字符ε,其余事件按事先制定的重标记规则进行标记;将事件重标记后得到的不确定有限状态自动机通过子集生成算法[15]转换为确定有限状态自动机,即为所求的结果GR。子集生成算法的功能为将不确定有限状态自动机转换为与其等价的确定有限状态自动机。对于任意字符串t∈Lm(GR),均存在s∈Lm(G),使得R(s)=t;反之,对于任意字符串s∈Lm(G),均有R(s)∈Lm(GR),所以Lm(GR)=R(Lm(G)),同理可得L(GR)=R(L(G))。在具有对称性的离散事件系统G中,被事件重标记映射标记为同一字符串的所有字符串进入的状态将生成一个状态子集。由于系统的对称性,所生成状态子集为对G中状态的一个等价划分[16],因此生成的状态子集总数量少于原系统的状态总数,即进行事件重标记后所得结果GR的状态数比G的状态数少。

2 抽象状态信息提取

本文研究的系统由n∈N组具有相同结构的组件组成,对于各组Gi,i∈{1,…,n}中的任意组件Gij,Gij′j,j′∈{1,…,|Gi|},λ(Gij)=λ(Gij′),即通过事件重标记映射忽略各组中组件个体差异。

本文制造系统如图2所示,系统中的组件划分为G1={Ii},i∈{1,…,m};G2={Oj},j∈{1,…,n},对所有i∈{1,…,m},j∈{1,…,n},将事件i11、i12、j21、j22分别重标记为11、12、21、22。本文所有的状态转移图中,用无源的单向箭头进入状态表示初始状态,用无目标状态的箭头出来状态表示标识状态,如果一个状态既是初始状态又是标识状态,则用双向箭头表示。

图2 本文制造系统示意图

在忽略组件个体差异后,针对防止缓冲区出现上溢或下溢的性能指标,需要获知各组中当前状态处于即将往缓冲区中放入工件的组件数量,即Ii中处于状态1的组件数量。为获得该数据,给出定义Ii=(Zi,ΣIi,δIi,zio,Zim),将其中取工件和往缓冲区中放入工件的事件分别记作σIil、σIiu。假定δIi(q,σIiu)=q′,拟放入工件事件集合为ΣIiq={σ∈ΣIi|σ≠σIiu,δIi(q,σ)!}。对于图2中的组件Ii,q=1,σIil=i11,σIiu=i12,ΣIiq=ø;对于图3中的组件Ii,q=1,σIil=i11,σIiu=i12,ΣIiq={i14}。ΣIi中其他事件因与缓冲区上溢或下溢无关可设为不可观测事件,在进行λ运算时这些事件被重标记为ε。

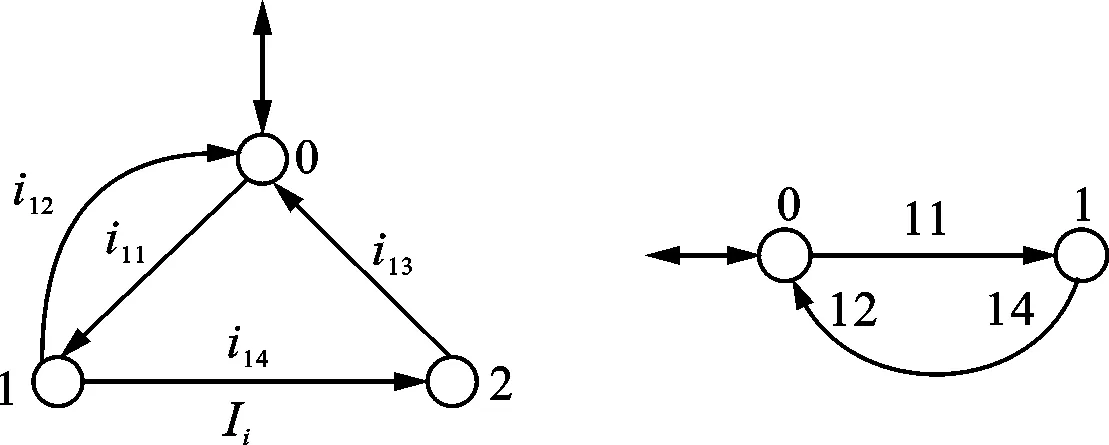
图3 复杂组件重标记前后的结构示意图

3 控制函数不变性研究

3.1 问题描述

经事件重标记映射计算得到的各组抽象状态信息可建立状态树结构模型,将自动机转换为状态树结构的具体过程可参见文献[8],然后通过STSLib软件计算得到各可控事件对应的控制函数。

对于基于抽象状态信息建立的状态树结构Gst与防止缓存区上溢与下溢的性能指标对应的谓词表达式P,假设利用STSLib软件计算得到各可控事件τi,对应的控制函数为fi,i∈{1,…,|Tc|},其中Tc=R(Σc):={τi}表示重标记后系统的可控事件集合。如果对任意数目的组件,控制函数fi保持不变,则称控制函数具有不变性。

3.2 并行工作系统控制函数不变性分析

对于图2中所示系统,各组中的组件均处于并行工作状态,利用事件重标记映射分别计算输入侧与输出侧的控制信息模型IR、OR。令m=3,n=1,经STSLib软件计算可得事件11、21的控制函数分别为f11、f21,如图4所示。其中,实线箭头代表逻辑真,虚线箭头代表逻辑假。

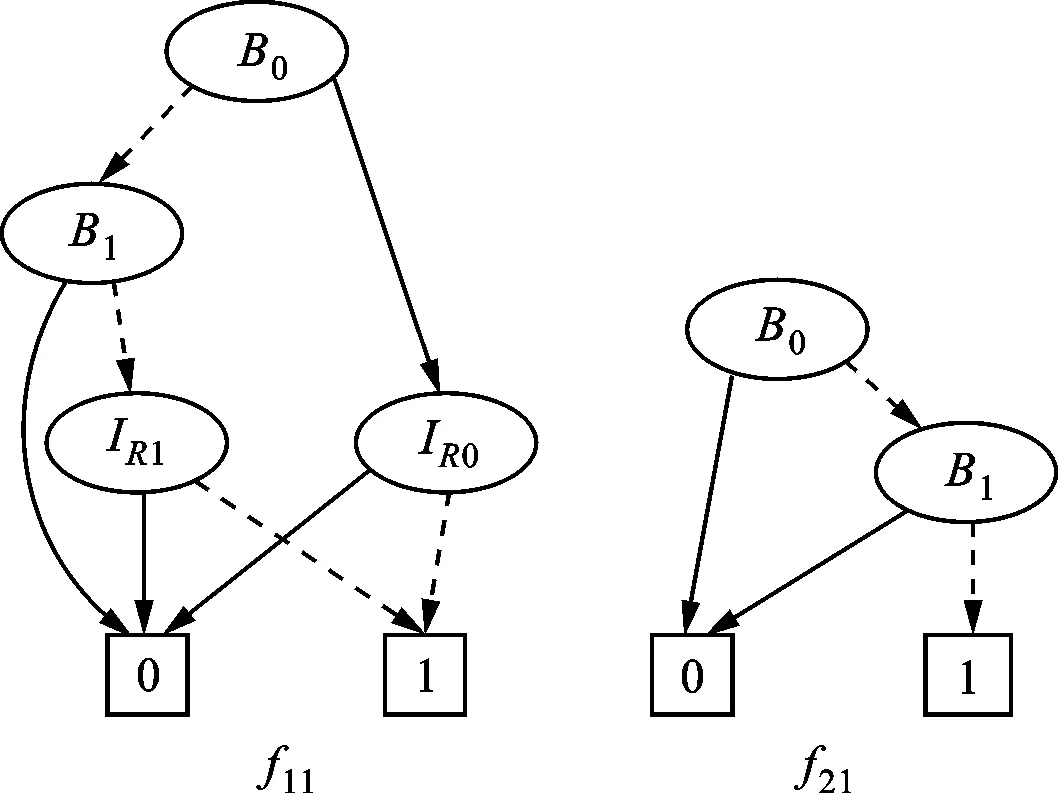
图4 控制函数f11、f21示意图

以f11为例,IR有4个状态,用IR0=0、IR1=0表示IR的当前状态为状态0,用IR0=1、IR1=0表示IR的当前状态为状态1,用IR0=0、IR1=1表示IR的当前状态为状态2,用IR0=1、IR1=1表示IR的当前状态为状态3。由于缓冲区B有3个状态,因此用B0=0、B1=0表示B的当前状态为状态0;用B0=1、B1=0表示B的当前状态为状态1;用B0=0、B1=1表示B的当前状态为状态2。箭头所指向的方框如果为0,则表示系统在当前状态组合下事件11(即各事件i11)不能发生;箭头所指向的方框如果为1,则表示系统在当前状态组合下事件11(即各事件i11)可以发生,此时缓冲区中有1个工件,输入侧无组件工作,可再允许输入侧1个组件取工件。

命题1 对任意m≥3,n≥1,f11,f21具有不变性。

系统对应的状态树结构模型Gst:=(St,H,T,Δ,b0,{b0}),如图5所示,其中重标记后事件集合T={11,12,21,22}。b0表示初始基本状态树,其中vRI=0,vRO=0,vB=0,即IR、OR、B均处于初始状态。由f11可知使能事件11的谓词为i+k<2,其中i∈{0,…,m},j∈{0,…,n},k∈{0,…,2},i、j分别表示输入侧与输出侧处于状态1的组件数量,k表示缓冲区中现有组件数量。

图5 状态树结构Gst

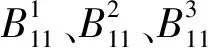
由于IR中仅有状态0、1、2可在系统运行过程中被访问到,因此B11不变,并且只有状态0、1允许事件11发生,因此B11可等价地表示成f11。f11可解读为:如果B0=0、B1=0缓冲区为空,当输入侧无组件处于状态1(IR0=0,IR1=0)或仅有1个组件处于状态1(IR0=1,IR1=0)时事件11被使能;如果B0=1、B1=0,即缓冲区已有1个工件,则输入侧无组件处于状态1(IR0=0,IR1=0)时事件11才能被使能;如果B0=0、B1=1,即缓冲区已满,则事件11不被使能,f11具有不变性。使能事件21的谓词为k=1或2,在缓冲区容量固定为2的前提下,对任意m≥3、n≥1该谓词保持不变,f21具有不变性。

由命题1可知,对任意数量的输入侧与输出侧组件m≥3、n≥1,输入侧组件开始工作(事件i11被使能)当且仅当f11使能事件11;输出侧组件开始工作(事件j21被使能)当且仅当f21使能事件21。由于f11、f21与m、n取值无关,因此控制函数具有不变性。

当m=1时,IR仅有2个状态,输入侧至多有1个组件处于状态1,因此只要缓冲区未满(B1=0),f11就可使能事件11。当m=2时,IR有3个状态,此时输入侧至多有2个组件处于状态1,当缓冲区为空时,不论输入侧组件处于何种状态,f11均可使能事件11。因此,m=1或2只是m≥3时的特殊情况。

针对防止缓存区上溢与下溢的性能指标,以m=9、n=9为例,文献[11]中计算得到的集中监督控制器有29 184个状态,其对应的重标记后的自动机有60个状态;相比之下,满足相同的性能指标,f11、f21比集中监督控制器更为简化。此外,集中监督控制器的规模将随着输入侧与输出侧组件数量的增多而增大,而f11、f21保持不变。

3.3 串行工作系统控制函数不变性分析

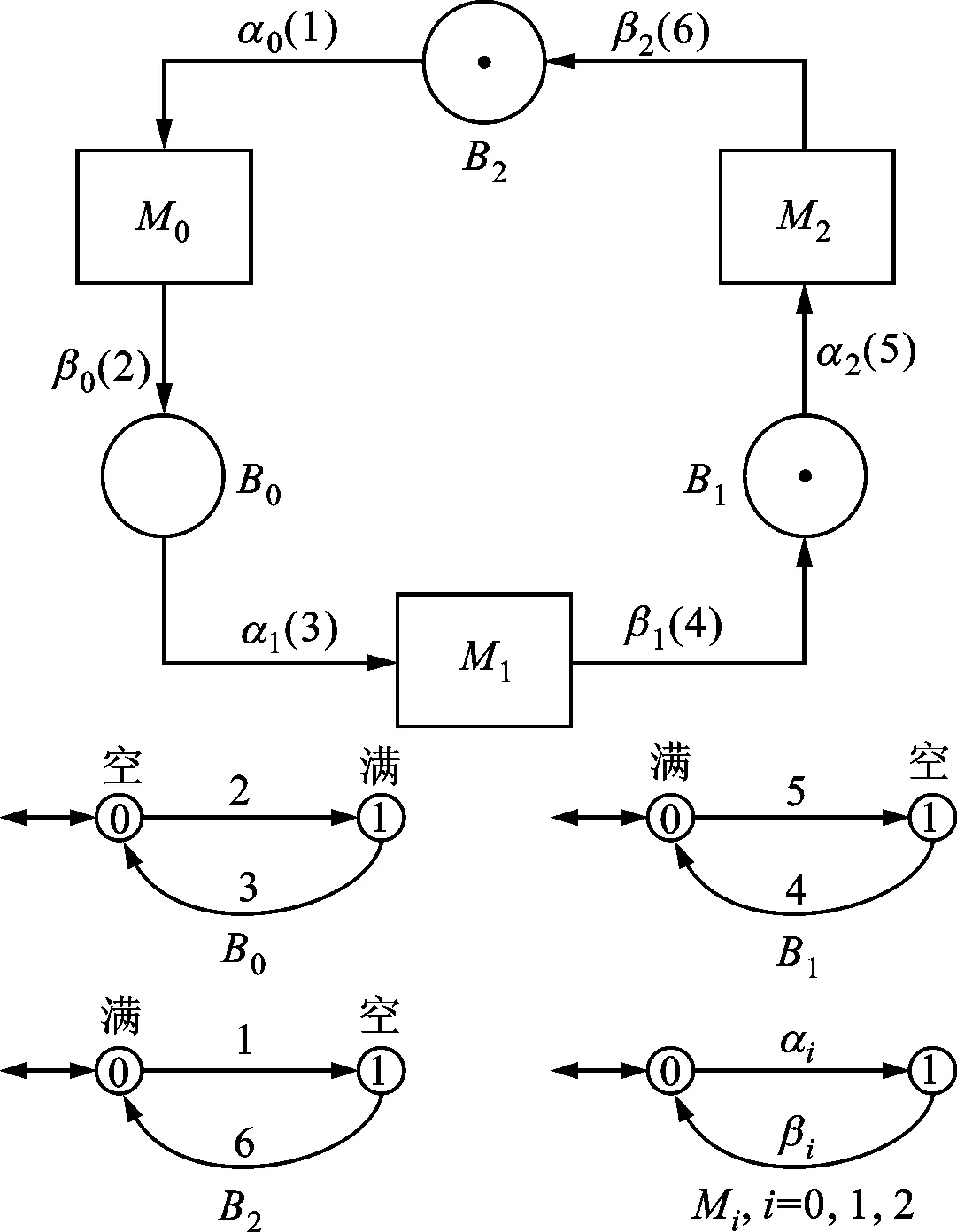
图6 具有对称性的串行工作系统及其自动机示意图

对于图6所示串行工作系统,文献[3]选用构建商自动机的方式对其进行化简,实现过程较为复杂,本文从控制函数不变性的角度直观地获得系统的控制逻辑,并结合系统对称性证明M0、M1、M2可由同一谓词进行控制。

该系统中,缓冲区B0、B1、B2的容量均为1,初始值分别为0,1,1;M0、M1、M2具有对称性。建立该系统的状态树结构模型可得图7所示的可控事件1、3、5的控制函数f1、f3、f5。由于f1、f3、f5只与缓冲区B0、B1、B2的状态(空或者满)有关,因此系统中可控事件的使能只取决于缓冲区状态(空或者满),而与各组件状态无关;由观察可知f1、f3、f5满足谓词P:αi,i∈{0,1,2}被使能当且仅当缓冲区Bi空、Bi⨁2满,其中i⨁2=(i+2)mod3。

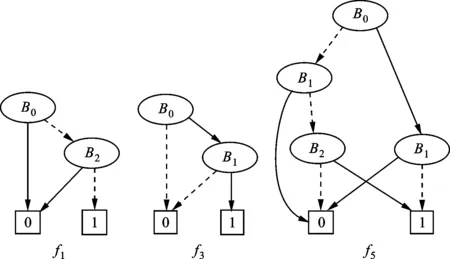
图7 控制函数f1、f3、f5示意图

命题2f1、f3、f5满足谓词P。

由命题2可知,可利用谓词P对各组件的运行进行监督控制,并且对于不同的缓冲区初始状态,谓词P均能防止各缓冲区出现上溢与下溢,因此具有不变性。

4 结 论

本文利用离散事件系统的对称性选用事件重标记映射提取各组组件的状态信息,然后基于状态信息构建状态树结构从而计算系统中可控事件对应的控制函数,并结合组件并行与串行工作的实例证明控制函数的不变性。由于控制函数具有不变性,在实际应用中可在组件增减时免于重复计算控制函数,且各组中重标记为同一事件的各可控事件可由同一控制函数进行使能,有效减小了控制函数的个数。相比于自动机形式的监督控制器,控制函数所需状态数更少。

本文所得的控制函数不变性建立在防止缓冲区出现上溢与下溢的性能指标之上,由于组件个体的细节与该性能指标无关,因此各组组件之间的交互不会影响到相应控制函数的选择,只要组件当前处于可控事件有定义的状态且控制函数允许该可控事件对应的重标记事件发生,就允许组件执行该可控事件。

[1] WONHAM W M. Supervisory control of discrete-event systems [EB/OL]. [2016-03-01]. http: ∥www.control.utoronto.ca/～wonham/.

[2] CASSANDRAS C G, LAFORTUNE S. Introduction to discrete event systems [M]. Berlin, Germany: Springer, 2008: 268-369.

[3] EYZELL J M, CURY J E R. Exploiting symmetry in the synthesis of supervisors for discrete event systems [J]. IEEE Transactions on Automatic Control, 2001, 46(9): 1500-1505.

[4] ROHLOFF K, LAFORTUNE S. The verification and control of interacting similar discrete event systems [J]. SIAM Journal on Control and Optimization, 2006, 45(2): 634-667.

[5] WANG W, SU R, LIN L. On analysis of deadlock and blocking freeness in isomorphic module systems [C]∥American Control Conference. Piscataway, NJ, USA: IEEE, 2013: 923-928.

[6] SU R. Discrete-event modeling of multi-agent systems with broadcasting-based parallel composition [J]. Automatica, 2013, 49(11): 3502-3506.

[7] BRYANT R. Graph-based algorithms for Boolean function manipulation [J]. IEEE Transactions on Computers, 1986, 35(8): 677-691.

[8] MA C, WONHAM W M. Nonblocking supervisory control of state tree structures [M]. Berlin, Germany: Springer, 2005: 11-125.

[9] MA C, WONHAM W M. Nonblocking supervisory control of state tree structures [J]. IEEE Transactions on Automatic Control, 2006, 51(5): 782-793.

[10]晁武杰, 甘永梅, 王兆安, 等. 实时状态树结构模型的最优非阻塞模块化监督控制研究 [J]. 西安交通大学学报, 2013, 47(4): 86-91. CHAO Wujie, GAN Yongmei, WANG Zhao’an, et al. An optimal nonblocking modular supervisory control to real-time state tree structures [J]. Journal of Xi’an Jiaotong University, 2013, 47(4): 86-91.

[11]JIAO T, GAN Y, YANG X, et al. Exploiting symmetry of discrete-event systems with parallel components by relabeling [C]∥TENCON 2015-2015 IEEE Region 10 Conference. Piscataway, NJ, USA: IEEE, 2015: 1-4.

[12]BHERER H, DESHARNAIS J, ST-DENIS R. Control of parameterized discrete event systems [J]. Discrete Event Dynamic Systems, 2009, 19(2): 213-265.

[13]GRIGOROV L, BUTLER B E, CURY J E R, et al. Conceptual design of discrete-event systems using templates [J]. Discrete Event Dynamic Systems, 2011, 21(2): 257-303.

[14]GRIGOROV L, CURY J E R, RUDIE K. Design of discrete-event systems using templates [C]∥Proceedings of the American Control Conference. Piscataway, NJ, USA: IEEE, 2008: 499-504.

[15]RABIN M O, SCOTT D. Finite automata and their decision problems [J]. IBM Journal of Research and Development, 1959, 3(2): 114-125.

[16]JIAO T, GAN Y, XIAO G, et al. Exploiting symmetry of state tree structures for discrete-event systems with parallel components [C]∥13th International Workshop on Discrete Event Systems. Piscataway, NJ, USA: IEEE, 2016: 97-102.

(编辑 赵炜)

Invariance Property of the Control Functions in Symmetric Discrete-Event Systems Modeled by State Tree Structures

JIAO Ting,GAN Yongmei,XIAO Guochun

(School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The symmetric discrete-event systems (DES) consist of groups of identical components. For such DES, the supervisor in the form of automata synthesized by the supervisory control theory often has large number of state and is nontransparent in control logic. Thus a computational approach of abstract control function is proposed. This approach fully exploits the symmetry of the system. For the performance index to avoid the underflow or overflow of buffers, the number of components in the status of processing finish is extracted with event relabeling map, thereby the processing details of each component are omitted. Then the abstract control functions are computed with the state tree structures (STS) based on the abstract status information. Finally, by illustrating examples of components working in parallel and serial, the invariance property of control functions are analyzed. Namely, with fixed buffer sizes, the status information required by the control function is irrelevant to the total number of components. The experimental results showed that by utilizing the invariance property of control functions, the repeated computation of control functions is avoided when identical components are added or deleted. Meanwhile, all controllable events relabeled by the same symbol can be enabled by one abstract control function; thus the number of control functions is reduced. Moreover, compared with the controller represented by automata, the control functions have fewer states and are more transparent in control logic.

discrete-event systems; supervisory control theory; state tree structures; control functions; predicate logic

2016-05-12。 作者简介:焦亭(1988—),男,博士生;甘永梅(通信作者),女,副教授。 基金项目:国家建设高水平大学公派留学生资助项目(留金发〔2014〕3026)。

时间:2016-09-14

10.7652/xjtuxb201611007

TP273

A

0253-987X(2016)11-0043-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160914.1805.006.html