中低速开关磁阻电机转矩优化策略研究

宋金龙,刘勇智,周政,范冰洁

(空军工程大学航空航天工程学院,710038,西安)



中低速开关磁阻电机转矩优化策略研究

宋金龙,刘勇智,周政,范冰洁

(空军工程大学航空航天工程学院,710038,西安)

为解决开关磁阻电机因其双凸极结构和严重非线性电感特性所导致的在换相和单相导通时转矩脉动较大的问题,提出了以转速、转矩和电流为控制量的模糊滑模多重闭环控制策略。速度环采用模糊滑模控制,通过积分变换将转速差转化为给定转矩,通过比较电机瞬时转矩与给定转矩,控制开关管的导通关断,实现转矩闭环控制;在电机换相时对同时导通的两相绕组进行转矩分配,建立转矩、电流和转子位置角的解析式,由分配的转矩求得给定的绕组电流进行电流闭环控制,从而达到对电机换相和单相导通时转矩脉动的有效抑制。仿真试验结果表明:在电机中、低速运行时,该控制系统与PID控制下的直接瞬时转矩控制(DITC)系统相比控制效果更好;电机低速运行时转矩波动稳定在±0.3 N·m以内,中速运行时转矩波动稍有增大,但仍维持在±0.8 N·m以内,实现了对转矩脉动的有效抑制。

开关磁阻电机;运动方程;转矩脉动;多重闭环控制;模糊滑模控制

开关磁阻电机结构简单、成本低、鲁棒性好,已被应用于航空航天、电动汽车等领域[1-2],但转矩脉动较大的缺点严重阻碍了其在更广领域的推广和普及。造成这一缺点的主要原因是电机换相时脉冲转矩的合成值不恒定,以及电机定转子特殊结构造成的严重非线性电磁特性。目前,抑制转矩脉动的方法主要有2类:一类是改进电机的本体设计;另一类是采用较为复杂的控制方法[3]。在电机的控制策略上主要有直接瞬时转矩控制(DITC)[3-6]、转矩分配函数控制[7-10]、迭代学习控制[11]等。电机本体改进方法有改变转子齿结构[11]等。文献[3-5]引入了直接瞬时转矩控制,但是需要查表求转矩模块,难以在工程中得到实际应用。文献[6]在借鉴传统DITC控制策略的基础上,运用智能算法抑制了转矩脉动,但基于柔性神经网络(FNN)的PID控制器存在计算时间较长的缺点。文献[7-10]应用转矩分配的方法确定了两相同时导通区间的转矩分配,抑制了转矩脉动,但该方法对电机的复杂建模和关键参数的测量精度依赖度很高,不利于推广。文献[11]采用了迭代学习控制,有效地抑制了转矩脉动。该方法无需预知电机的精确模型,但对处理器内存要求较高。文献[12]对电机本体进行了改进,通过在转子齿两侧开槽、改变转子表面磁密方向来有效减小转矩脉动。文献[13]将滑模变结构控制(VSS)应用于开关磁阻电机调速系统(SRD)中,但这种方法只是对速度环进行了变结构控制。文献[14]通过继电反馈求解电机传递函数,并设置电流控制器对转矩进行了有效抑制。

本文在直接瞬时转矩控制的基础上,提出了以转速、电流和转矩为控制量的多重闭环控制策略,首先通过模糊滑模控制和积分变换将电机的转速差转变为参考转矩,建立电流、转子位置角和转矩的对应关系,检测电机的相电流,并将其转换为相转矩,通过相转矩与参考转矩的比较来控制开关管的通断。这种方法能够对电机两相和单相运行时的转矩脉动进行抑制,而且解决了查表求解转矩难以在实际中得到应用的问题,同时也降低了通过开关管的电流峰值,实现了对电机的循环控制。最后,通过仿真试验验证了该方法的可行性。

1 解析法求瞬时转矩

很多文献中都是通过查询T-i-θ三维表格来获得开关磁组电机(SRM)的瞬时转矩,这种方法需要占用较大的内存,而且不利于工程应用。为此,本文研究了瞬时转矩的解析法求解,以便更好地应用于工程实践。

电机相绕组产生的转矩

(1)

式中:Tk为第k相转矩;Ψ为该相磁链;θ为转子位置角;ik为第k相电流;Lk为第k相电感。由式(1)可知,通过电感、电流和转子位置角即可获得转矩信息。电流和转子位置角可以通过传感器获得,所以求解转矩转变为对电感的精确求解。

1.1 电感模型

当开关磁阻电机工作在饱和状态时,其非线性电感可以由傅里叶级数近似逼近[15]

φk)

式中:Lk(θ,i)为第k相电感;Nr为转子齿数;φk为第k相电感的谐波分量。傅里叶级数项的系数表示电感与电流的关系,级数项则表示电感与转子位置角的关系。因为相电感的谐波分量远小于基波分量,可以忽略,所以相电感可近似为

(2)

傅里叶级数项系数可以由特殊位置的电感表示。针对电感的非线性特性,取特殊位置0°、22.5°、45°时的电感为基准值,记为Lm(m=1,2,3),则级数项系数

(3)

其余特征位置的电感与电流的关系可以用多项式级数近似

Lm(i)=am0+am1i+am2i2

(4)

式中:amr(r=0,1,2)为拟合参数;Lm=1为转子凹槽中心线与定子凸极中心线对齐时的电感值,此时铁芯不饱和,可认为Lm=1为常数。

经过仿真计算,可以得到各特征位置的电感、电流拟合参数的值,见表1。通过检测多个位置的电感,并结合式(2)～式(4),可以求得参数pnm(n=0,1,2;m=1,2,3)分别为[0.25,0.5,0.25;0.5,0,-0.5;0.25,-0.5,0.25]。

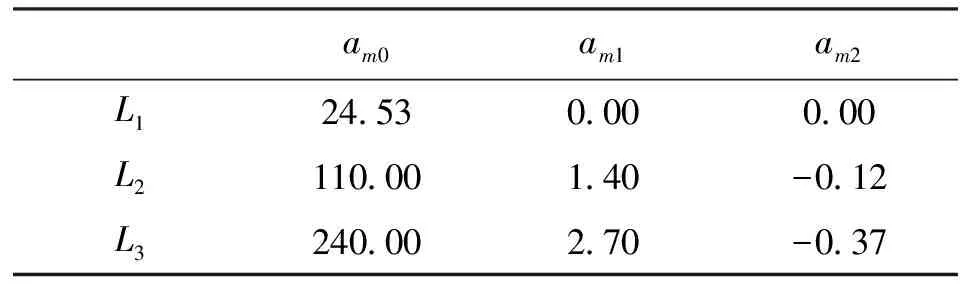
表1 电感电流拟合参数值(m=1,2,3) 10-4

由电机各相开关管的开通关断规律可知,开关管的开通区间大部分落在0°～45°范围内,而且转矩主要产生在15°～30°区间。当转子位置在15°～30°和60°～75°区间内时,电感近似为线性[16],而且当绕组电流较小时,电流的变化对电感产生的影响较小,所以在电感线性区间内将电流近似为常数,将电感只与转子位置角拟合,拟合公式为

Lk(θ,i)=b0+b1θ+b2θ2+b3θ3|i≈const

(5)

在60°～75°区间内电感与转子位置角的拟合结果如图1所示。

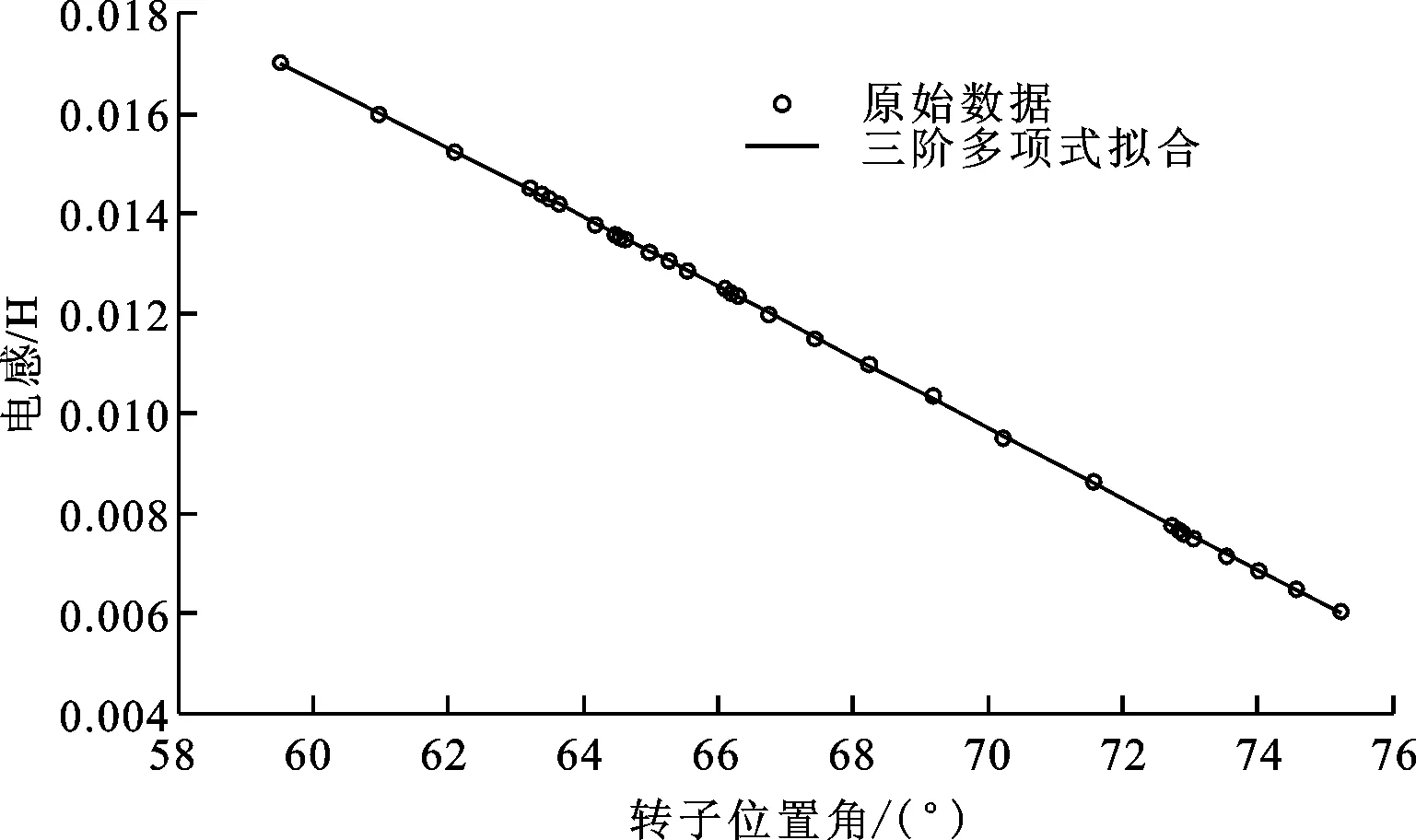
图1 电感与转子位置角的拟合曲线

综上所述,电感的求解公式为

将按照上式计算得到的电感与有限元软件ANSOFT解算得到的实际电感进行对比,结果如图2所示,可见解析法求得的电感整体精度较好。由于电机的转矩主要产生在电感的近似线性区附近,所以可以用此方法来求解瞬时转矩。

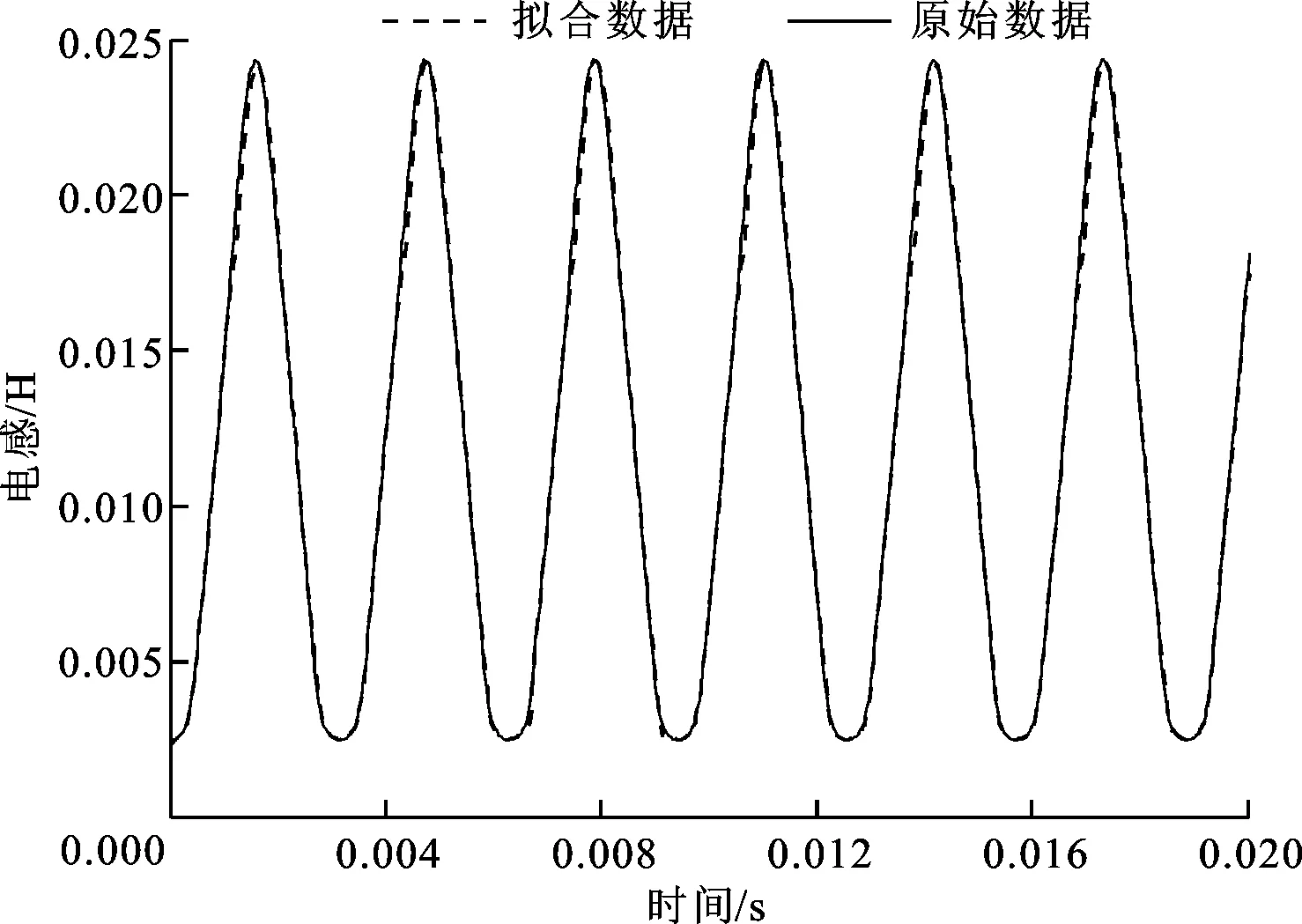
图2 实际电感与求得电感的对比

1.2 转矩求解

电机的相绕组电压

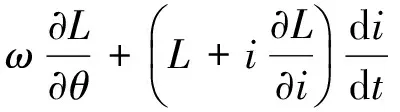
(6)

在电感线性区内电机磁路不饱和,忽略电流对电感的影响,式(6)可简化为

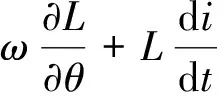
(7)

再经过化简,可以得到

ω

(8)

当电机运行在电感的非线性区间内时,将式(2)代入式(1)即可求得此时电机产生的转矩。综上,电机的瞬时转矩求解方程如下

(9)

2 控制策略

控制系统采用电流、转矩、转速多重闭环的控制策略,兼顾了电机两相导通和单相导通时的转矩脉动抑制,其整体框图如图3所示。常规的瞬时转矩检测存在设备烦琐、方法不易实现的问题,而本控制系统只需检测开关磁阻电机的瞬时相电流和转子位置角,并通过计算将其转换为相输出转矩(必要时需检测相电压),因此设备简单,易于工程应用。

图3 多重闭环控制系统的整体结构图

开关磁阻电机工作时的相电流如图4所示,以第N相为例,AC段为开关管导通区间,CD段为续流区间,EF段为单相导通区间。只要电流不为0,就会产生转矩。很多文献没有考虑续流阶段转矩的变化,使得对转矩控制不够精确。多重闭环控制系统能够实时检测相电流并求得其产生的转矩,通过相转矩与参考转矩的比较来控制开关管的通断,可达到对转矩的准确控制。系统将每相电流分为2个区间,t1～t3区域为区间Ⅰ,t3～t5区域为区间Ⅱ,如图5所示,区间的分界点为t3,即前一相电流为0的时刻。在区间Ⅰ内主要对第N-1相和第N相进行控制,在区间Ⅱ内主要对第N相和第N+1相进行控制,且两者的控制方式完全相同。

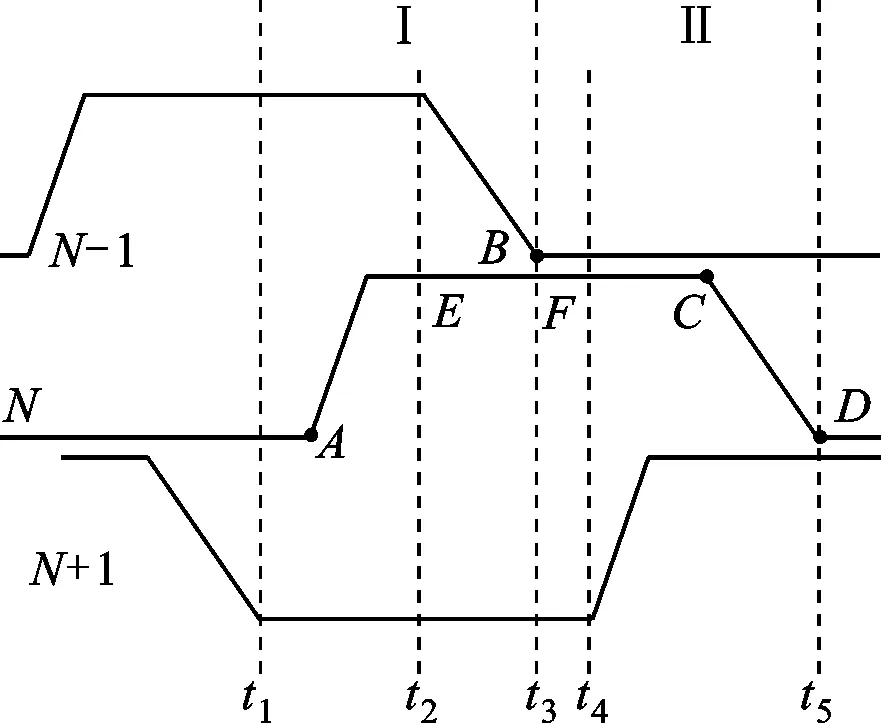
图4 开关管导通区间的划分

在区间Ⅰ内,系统首先通过模糊滑模控制和积分变换将转速差转换为参考转矩,然后将检测得到的转子位置角和瞬时相电流代入式(9),得到第N-1相的瞬时转矩,并与参考转矩进行比较,如果相转矩大于参考转矩(允许误差范围为[-0.1 N·m,0.1 N·m),则直接控制该相的功率管使其工作在“0”状态(2个绝缘栅双极型晶体管(IGBT)中一个导通,另一个关断),如果还是大于参考转矩,则使其工作在“-1”状态(2个IGBT都关断)。如果第N-1相的瞬时转矩小于参考转矩:

(1)若第N相转子位置角处于[θon,θoff]区间内,则通过该相的转子位置角(N相与N-1相转子位置角互差Δθ电角度)和转矩差可以求得N相的参考电流iNref,将参考电流和检测得到的该相电流进行对比(允许误差范围为[-0.05 A,0.05 A]),如果瞬时电流小于参考电流,则使功率管的工作状态加1,直到“1”状态(2个IGBT都导通)为止,如果瞬时电流大于参考电流,则使功率管的工作状态减1,直到“-1”状态为止。

(2)如果第N相转子位置角没有处于[θon,θoff]区间内,则依旧调节第N-1相的功率管触发信号,使其工作状态加1,直到“1”状态为止。

区间Ⅱ内的控制方式同理,这里不再赘述。这种控制方式兼顾了电机两相导通和单相导通的转矩脉动抑制情况,既保留了DITC方式的瞬时性,也能够在一定程度上实现对通过开关管的电流峰值的削减,而且可实现对各相的循环控制,有利于电机的平稳运行。

3 模糊滑模控制器设计

滑模控制具有鲁棒性强、受外界干扰影响小的优点,已被广泛应用于航空航天和电机的伺服控制系统中。但是,变结构的不连续开关特性会引起系统的抖振,因此本文将模糊控制与滑模控制相结合,再经过积分环节将转速差转变为参考转矩,以减小系统的抖振[17],改善系统的控制效果。

3.1 建立状态方程

电机的运动方程为

(10)

(11)

式中:θ为转子位置角;ω为转子角速度;J为转动惯量;Tk为第k相的电磁转矩;TL为负载转矩;F为阻尼系数;q为电机相数。经推导可得

(12)

转换为状态变量的形式

(13)

式中:x1=ωref-ω;x2=dω/dt;U为滑模控制量,可通过积分环节转化为参考转矩

(14)

其中τ为采样时间,Tref为参考转矩。

3.2 切换函数和控制率设计

(15)

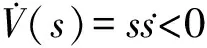
3.3 模糊滑模控制设计

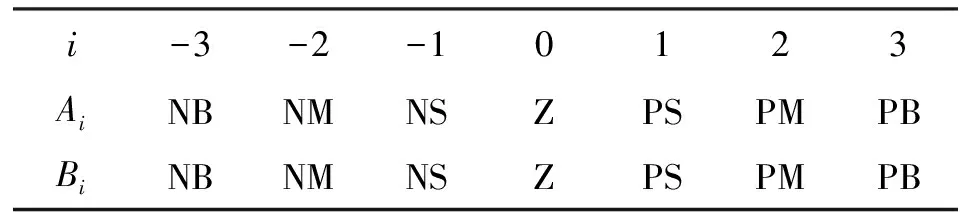
表2 模糊控制规则表

定义规则如下

ifsisAithenΔkisBi(i=-3,…,3)

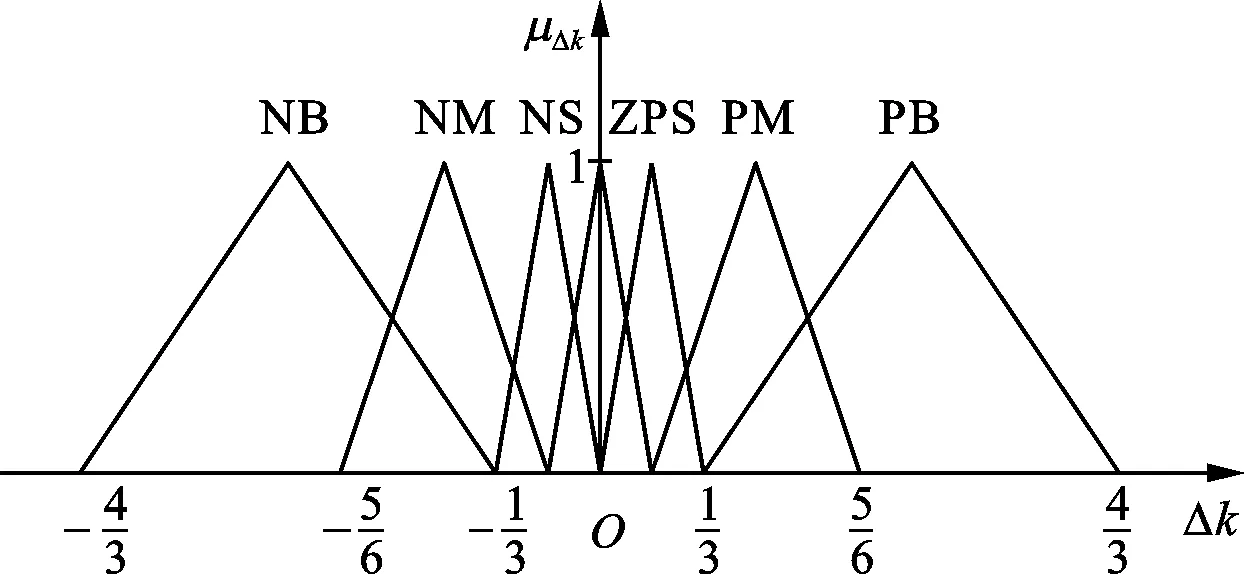
图5 Δk的隶属度函数

根据图5所示的Δk隶属度函数以及上述模糊控制规则,采用代数积分-MAX-重心法求解模糊切换增益,从而将模糊输出转化为精确的控制量

(16)

通过以上方法,可以将模糊切换增益转化为s的函数,具体如下

Δk=

4 仿真试验

在MATLAB/Simulink中搭建6/4电机模型,本体采用查表的形式设计,其转矩、电流和转子位置角的关系由有限元软件ANSOFT解析求得,如图6所示。

图6 开关磁阻电机的转矩曲线族

搭建模型时,选取电机的额定电压为270 V,额定功率为3 kW,额定转速为3 000 r/min。设定额定电压270 V、额定功率3 kW等相关参数进行仿真,当给定转速为500 r/min、负载转矩为6 N·m以及给定转速为2 000 r/min、负载转矩为16 N·m时,模糊滑模多重闭环控制(简称多重闭环控制)下的转矩与PID控制下的DITC控制系统(简称PID控制系统)的输出转矩的对比如图7所示,可见相比PID控制系统,多重闭环控制的效果更好,而且响应快,超调较小。

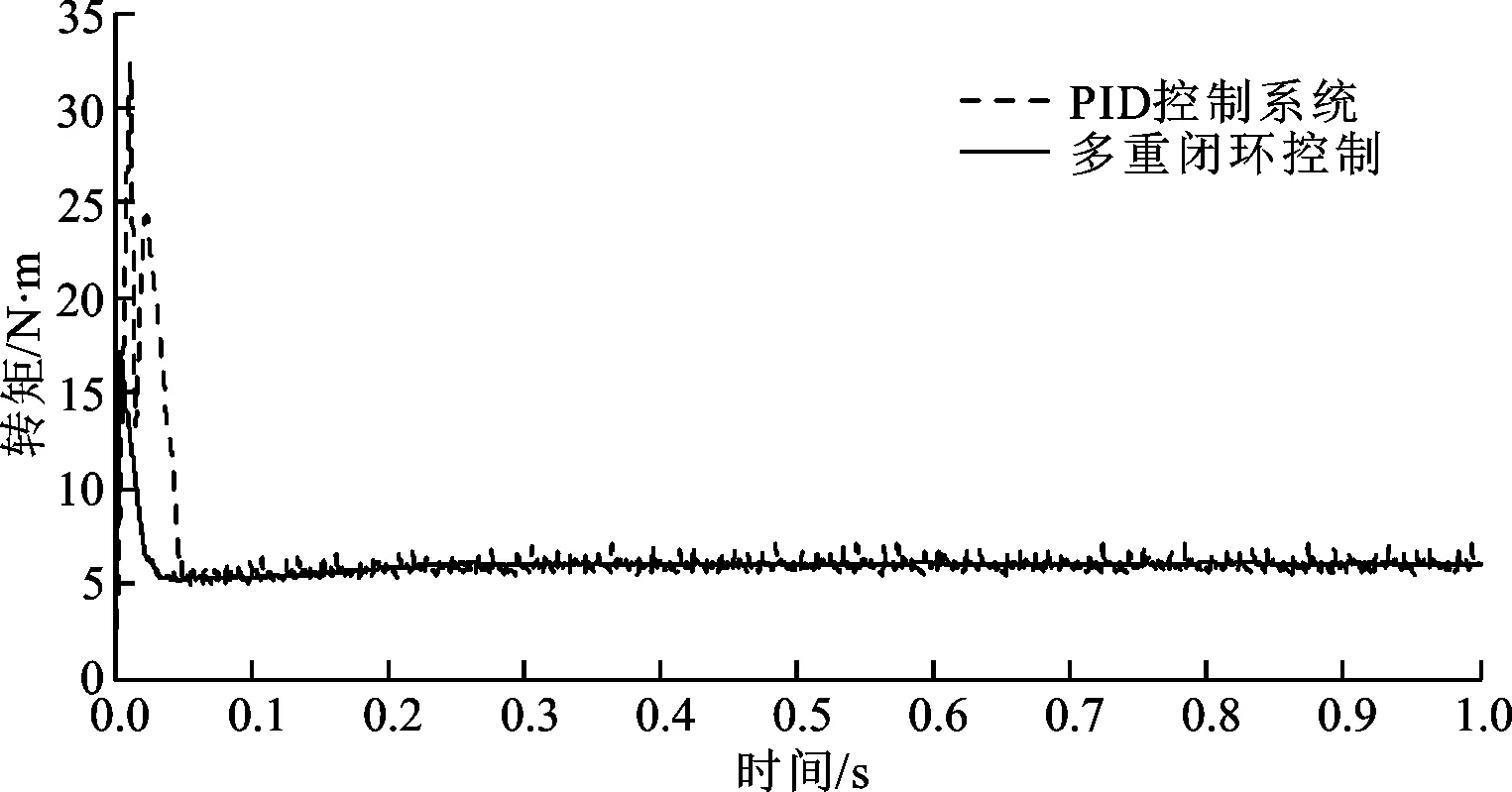
(a)转速为500 r/min,负载转矩为6 N·m

(b)转速为2 000 r/min,负载转矩为16 N·m图7 2种控制方式的输出转矩对比图

为验证本文针对转矩脉动提出的多重闭环控制策略的可行性,在一台3 kW三相6/4结构SRM的控制平台上进行了试验。以德州仪器公司(TI)的TMS320F2812-150MHz型数字信号处理器(DSP)为核心控制芯片,通过模糊滑模控制转速差,将积分变换转换为参考转矩,并且利用DSP控制器中的软件来实现转矩-电流-转速多重闭环控制。用12位ADC采样芯片ADS7864进行实时采样,以获得电压、电流信息,采样周期为20 μs。通过光电式位置传感器获得电机的转子位置角和转速信息。功率变换器采用不对称半桥电路,主开关器件采用IGBT。样机的结构参数如下:定子极数为6;转子极数为4;定子极弧为0.5;转子极弧为0.355;铁芯叠长为76 mm;匝数为52;定子外径为138 mm;定子内径为72.3 mm;转子外径为71.4 mm;转子内径为20 mm;定子轭高为11.94 mm;转子轭高为12 mm;气隙尺寸为0.4 mm;硅钢片型号为DW360_50。

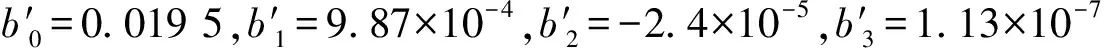
在滑模控制中增加了模糊控制,旨在减小系统抖振,但是模糊切换增益求解复杂,无疑增加了瞬时转矩的求解时间,难以保证实时性。因此,在试验之前对模糊切换增益进行了求解,按照Δk的求解公式,得到s∈(-1,1]范围内Δk的取值,如图8所示。为了保证实时性,试验时对模糊切换增益的取值做了简化处理:将s的取值范围分为更小的区间,在极小区间内直接对模糊切换增益赋值,如当s∈(-1,-0.95]时,Δk=-0.34。这样就省去了根据隶属度函数、模糊控制规则等求解模糊切换增益的时间,从而保证了试验的实时性。

图8 s∈(-1,1]时的模糊切换增益

设定电机的转速为500 r/min,初始负载转矩为6 N·m,在1.0 s时将负载转矩提高到7 N·m,得到电机在上述2种控制方式下运行时的转速和转矩对比,如图9所示。分析可知:多重闭环控制比PID控制系统响应快、超调小;PID控制系统的转矩脉动为-0.5～1.1 N·m,而多重闭环控制将转矩脉动减小至±0.3 N·m以内,实现了较精确的控制。

将电机转速提高到2 000 r/min,并在1.0 s时将负载转矩由16 N·m提高到20 N·m,来检验多重闭环控制的效果,结果如图10所示。分析可知,当负载转矩在16和20 N·m时,由于转速较高、电流较大,使得多重闭环控制的精度有所下降,电机转矩脉动维持在±0.8 N·m以内,但相比PID控制系统的±2 N·m仍有一定提高,而且响应较快。

由试验结果可以看出,多重闭环控制在电机中低速运行时实现了对转矩脉动的较好抑制,而且转速波动很小,改善了电机的运行性能。

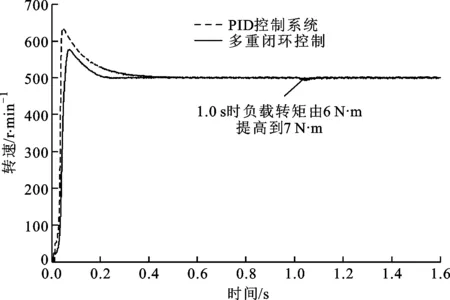
(a)电机转速波形

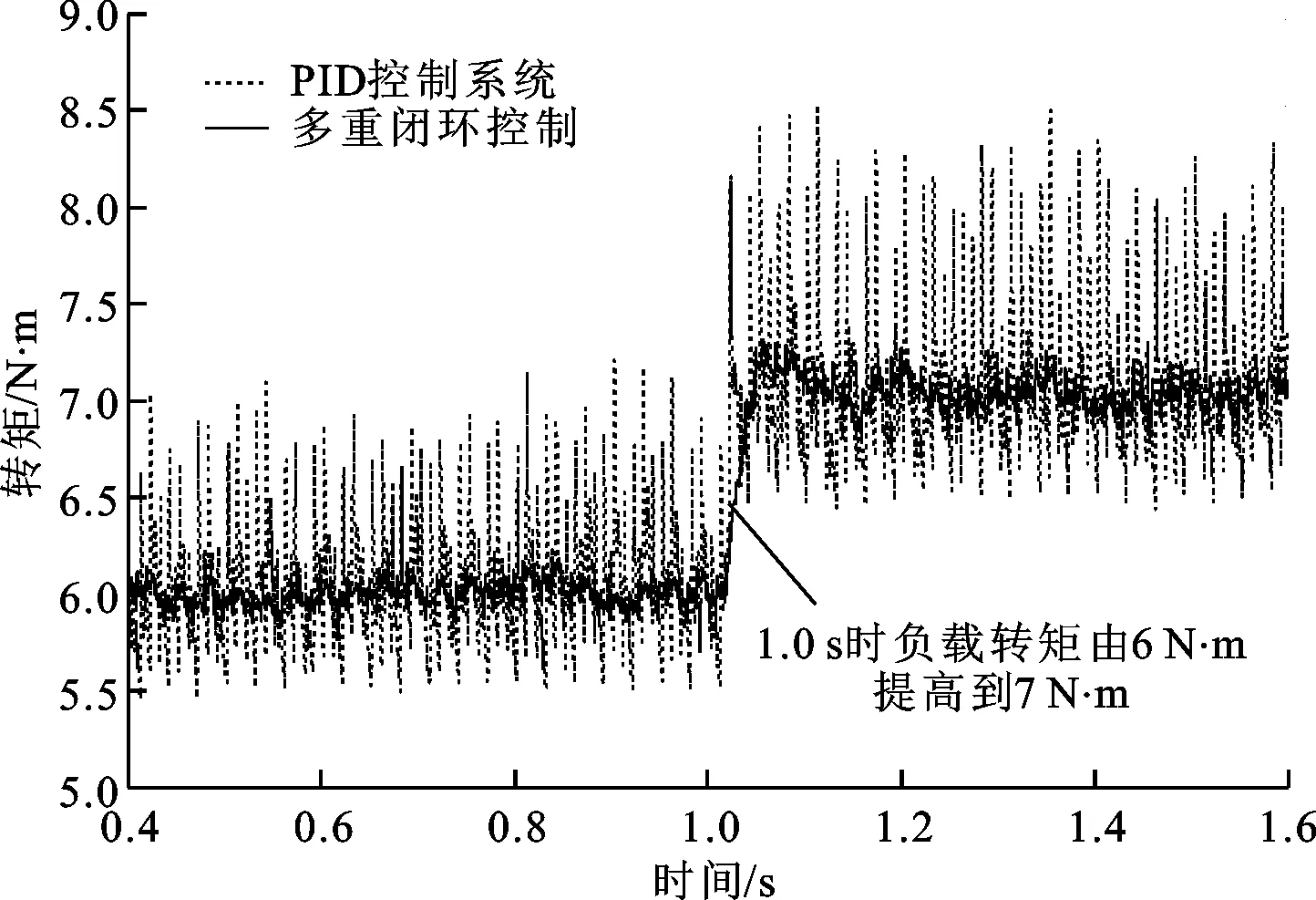
(b)稳定后的电机转矩波形图9 电机低速运行时的试验波形

(a)电机转速波形

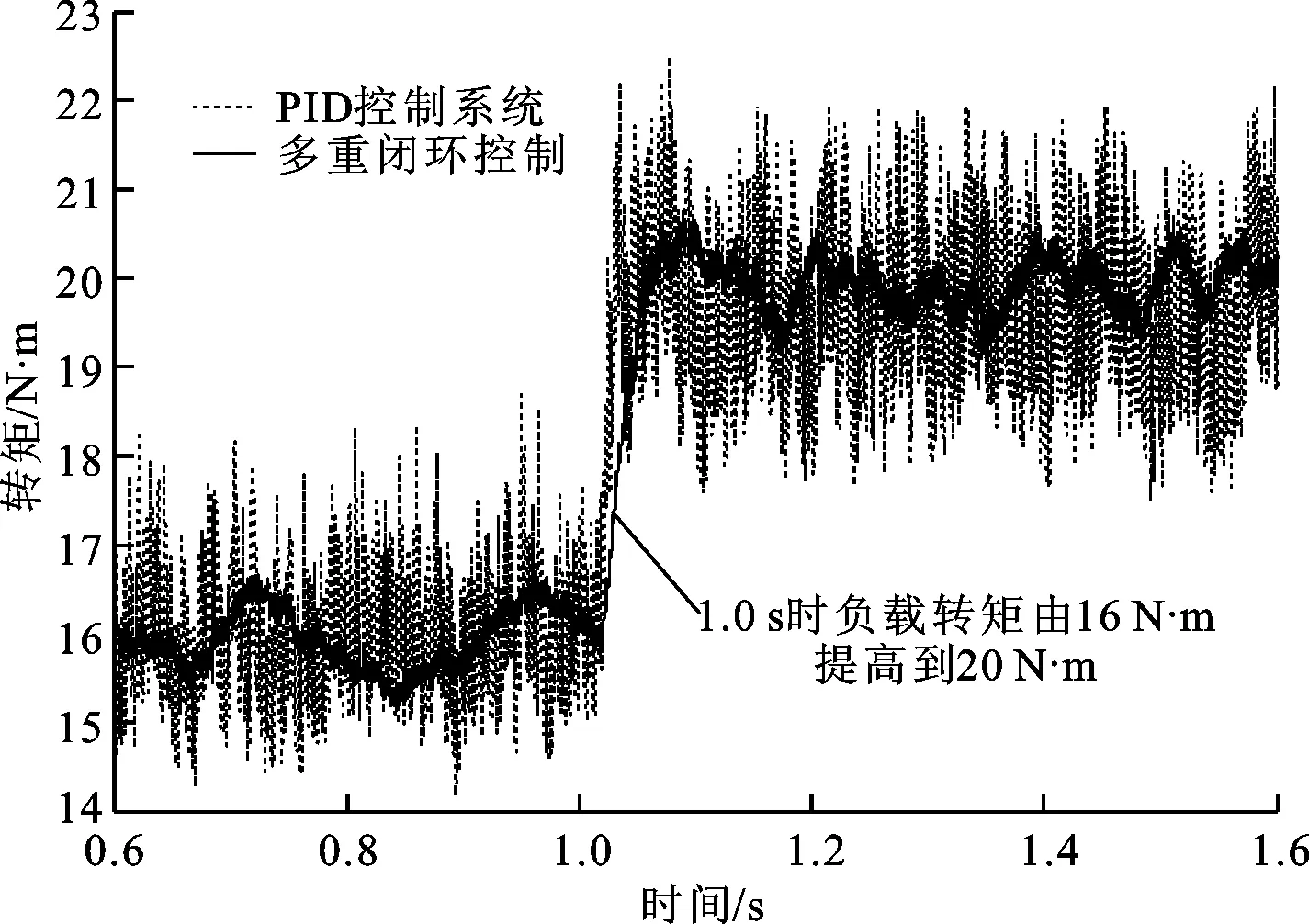
(b)稳定后的电机转矩波形图10 电机中速运行时的试验波形

5 结束语

本文通过模糊滑模控制和积分变换将转速差转变为参考转矩,并且建立了电流、转子位置角和转矩之间的电机运动方程;提出了以电流、转速和转矩为控制量的多重闭环控制策略,可以通过测量电机的相电流求得相转矩,再与参考转矩进行比较,实现对相邻两相开关管的控制,在两相同时导通和单相导通的情况下抑制转矩脉动,改善电机的运行性能。

[1] 丁文, 梁得亮, 鱼振民, 等. 基于磁链与转矩特性的开关磁阻电机建模研究 [J]. 西安交通大学学报, 2007, 41(2): 214-218. DING Wen, LIANG Deliang, YU Zhenmin, et al. Modeling for switched reluctance motor based on flux linkage and torque characteristics [J]. Journal of Xi’an Jiaotong University, 2007, 41(2): 214-218.

[2] 隋宏亮, 梁得亮, 丁文. 互感耦合开关磁阻电机的等效磁路模型与有限元分析 [J]. 西安交通大学学报, 2010, 44(4): 71-75. SUI Hongliang, LIANG Deliang, DING Wen. Equivalent magnetic circuit model and finite element analysis of mutually coupled switched reluctance machine [J]. Journal of Xi’an Jiaotong University, 2010, 44(4): 71-75.

[3] 漆汉宏, 张婷婷, 李珍国, 等. 基于DITC的开关磁阻电机转矩脉动最小化研究 [J]. 电工技术学报, 2007, 22(7): 136-140. QI Hanhong, ZHANG Tingting, LI Zhenguo, et al. SRM torque ripple minimization based on direct instantaneous torque control [J]. Transactions of China Electrotechnical Society, 2007, 22(7): 136-140.

[4] 李珍国, 阚志忠. 开关磁阻电机的高效率直接瞬时转矩控制 [J]. 电工技术学报, 2010, 25(8): 31-37. LI Zhenguo, KAN Zhizhong. A high efficiency direct instantaneous torque control of SRM [J]. Transactions of China Electrotechnical Society, 2010, 25(8): 31-37.

[5] NISAI H F, MARCUS M, ROBERT B I. High-dynamic four-quadrant switched reluctance drive based on DITC [J]. IEEE Transactions on Industry Applications, 2005, 41(5): 1232-1242.

[6] 党选举, 袁小唐, 胡景佳. 基于柔性神经网络的SRM直接瞬时转矩控制 [J]. 电气传动, 2014, 44(5): 62-66. DANG Xuanju, YUAN Xiaotang, HU Jingjia. Direct instantaneous torque control of SRM based on flexible neural network [J]. Electric Drive, 2014, 44(5): 62-66.

[7] 刘勇智, 朱晨承, 王宇. 基于不对称式TSF的开关磁阻电动机转矩脉动抑制 [J]. 微特电机, 2014, 42(8): 86-89. LIU Yongzhi, ZHU Chencheng, WANG Yu. Torque ripple reduction of switched reluctance motor based on the asymmetry TSF [J]. Small & Special Electrical Machines, 2014, 42(8): 86-89.

[8] 张炳力, 戚永武, 徐国胜. 开关磁阻电机转矩分配策略的优化 [J]. 合肥工业大学学报(自然科学版), 2012, 35(12): 1615-1619. ZHANG Bingli, QI Yongwu, XU Guosheng. Torque-sharing strategy optimization of switched reluctance motor [J]. Journal of Hefei University of Technology (Natural Science), 2012, 35(12): 1615-1619.

[9] ISHIKAWA H, KOMAKI R, NAITOH H, et al. Electric transfer function model of switched reluctance motors and model-based current control design [J]. Electrical Engineering in Japan, 2010, 173(1): 51-59.

[10]VLADAN P V. Minimization of torque ripple and copper losses in switched reluctance drive [J]. IEEE Transactions on Power Electronics, 2012, 27(1): 388-399.

[11]潘再平, 罗星宝. 基于迭代学习控制的开关磁阻电机转矩脉动抑制 [J]. 电工技术学报, 2010, 25(7): 51-55. PAN Zaiping, LUO Xingbao. Torque ripple minimization of switched reluctance motor based on iterative learning control [J]. Transactions of China Electrotechnical Society, 2010, 25(7): 51-55.

[12]张鑫, 王秀和, 杨玉波, 等. 基于转子齿两侧开槽的开关磁阻电机振动抑制方法研究 [J]. 中国电机工程学报, 2015, 35(6): 1508-1515. ZHANG Xin, WANG Xiuhe, YANG Yubo, et al. Vibration reduction of a switched reluctance motor using new rotor tooth with slot on each side [J]. Proceedings of the CSEE, 2015, 35(6): 1508-1515.

[13]黄操, 张奕黄. 开关磁阻电机的滑模变结构控制 [J]. 电力自动化设备, 2006, 26(12): 35-37. HUANG Cao, ZHANG Yihuang. Variable-structure control of switched reluctance motor [J]. Electric Power Automation Equipment, 2006, 26(12): 35-37.

[14]DOS REIS L L N, COELHO A A R, ALMEIDA O M, et al. Modeling and controller performance assessment for a switched reluctance motor drive based on set point relay [J]. ISA Transactions, 2009, 48: 206-212.

[15]吴红星. 开关磁阻电机系统理论与控制技术 [M]. 北京: 中国电力出版社, 2010: 30-36.

[16]蔡骏, 邓智泉. 基于电感线性区模型的开关磁阻电机无位置传感器技术 [J]. 中国电机工程学报, 2012, 32(15): 114-123. CAI Jun, DENG Zhiquan. Sensorless control of switched reluctance motors based on phase inductance model in linear regions [J]. Proceedings of the CSEE, 2012, 32(15): 114-123.

[17]刘金琨. 滑模变结构控制MATLAB仿真 [M]. 北京: 清华大学出版社, 2005: 22-30.

[本刊相关文献链接]

闻德生,甄新帅,陈帆,等.变频电机-多输出泵调速回路速度特性分析.2016,50(10):99-103.[doi:10.7652/xjtuxb201610 015]

王悍枭,刘凌,吴华伟.改进型滑模观测器的永磁同步电机无传感器控制策略.2016,50(6):104-109.[doi:10.7652/xjtuxb201606016]

宋保维,李玉凯,程博.集成电机推进器用无刷直流电机齿槽转矩削减新方法.2016,50(5):151-156.[doi:10.7652/xjtuxb201605023]

常雪剑,彭博,刘凌,等.新型非奇异终端滑模观测器的永磁同步电机无传感器控制.2016,50(1):85-91.[doi:10.7652/xjtuxb201601014]

张蕾,张爱民,景军锋,等.静止无功补偿器与发电机励磁系统的自适应鲁棒协调控制策略.2015,49(11):96-101.[doi:10.7652/xjtuxb201511016]

李彪,李黎川.新型磁链观测算法及其在永磁同步电机无位置传感器控制中的应用.2015,49(11):102-109.[doi:10.7652/xjtuxb201511017]

陈起旭,徐俊,杨松,等.大功率盘式交流永磁同步电机电磁场分析.2015,49(9):120-125.[doi:10.7652/xjtuxb201509 020]

马成方,杨晓君,张俊,等.面向运动平稳性的直线电机推力频谱特征分析.2015,49(8):45-51.[doi:10.7652/xjtuxb 201508008]

高建平,葛坚,赵金宝,等.复合电源系统功率分配策略研究.2015,49(7):17-24.[doi:10.7652/xjtuxb201507004]

常雪剑,刘凌,崔荣鑫.永磁同步电机非奇异快速终端可变边界层滑模控制.2015,49(6):53-59.[doi:10.7652/xjtuxb 201506009]

郝双晖,王磊,宋宝玉,等.交流伺服系统永磁同步电机电流及位置二级状态观测器设计.2015,49(5):100-107.[doi:10.7652/xjtuxb201505016]

续丹,包鑫,霍小宁,等.永磁同步电机宽速域无位置传感器控制.2013,47(9):60.[doi:10.7652/xjtuxb201309010]

(编辑 葛赵青)

Torque Optimization of Medium-Low Speed Switched Reluctance Motors

SONG Jinlong,LIU Yongzhi,ZHOU Zheng,FAN Bingjie

(Aeronautics and Astronautics Engineering College, Air-Force Engineering University, Xi’an 710038, China)

Switched reluctance motor with double salient structure and nonlinear inductance characteristics may be subject to torque ripple when working in the states of switching and single-phase conducting. In view of this, a fuzzy sliding-mode multiplex-loop control system with control quantities of speed, torque and current is designed, in which fuzzy sliding-mode control is adopted for speed loop and the speed difference is transformed into given torque through integral transformation. By comparing instantaneous torque with the given torque, switching tubes will be controlled to realize torque’s closed-loop control. The torque is distributed to the windings of two simultaneously conducted phases during the commutation of motor and the equations of torque, current and rotor position angle are established. The winding currents will be obtained via the distributed torque to realize current’s closed-loop control. Therefore, the torque ripple can be depressed effectively during the commutation and single-phase conducting. Simulation and experimental results show that the proposed method has a better control effect than the direct instantaneous torque control (DITC) with PID at low speeds, and the torque ripple can be stabilized within ±0.3 N·m, while becoming slight greater at medium speeds but within the range of ±0.8 N·m. So the torque ripple is depressed effectively by the proposed method.

switched reluctance motor; motion equation; torque ripple; multiple-loop control; fuzzy sliding mode control

2016-03-25。 作者简介:宋金龙(1991—),男,硕士生;刘勇智(通信作者),男,博士,教授。 基金项目:国家自然科学基金资助项目(61074007);陕西省自然科学基金资助项目(S2015YFJM0413)。

时间:2016-09-23

10.7652/xjtuxb201611013

TM352

A

0253-987X(2016)11-0083-08

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160923.1549.006.html