投影仪全参数平面线性估计的高精度标定方法
龚春园,梁晋,温广瑞,牌文延,李磊刚
(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.广东顺德西安交通大学研究院,528300,广东佛山)
投影仪全参数平面线性估计的高精度标定方法
龚春园1,2,梁晋1,2,温广瑞1,2,牌文延1,2,李磊刚1,2
(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.广东顺德西安交通大学研究院,528300,广东佛山)
针对投影仪光路结构复杂、主点偏差大导致高精度标定难以实现的问题,提出一种全参数平面线性估计的方法,为投影仪标定过程提供精确的主点偏差初值,实现了投影仪的全参数高精度标定。首先将投影仪作为虚拟相机,利用多频相移原理得到投影仪和标定板的坐标对应关系,然后采用两步法对非线性方程进行求解计算,通过引入向量参数的方法实现非线性方程的线性化,再利用仿射变换关系选取最优点集,得到稳定的直接参数预估算法,最后利用一种全局捆绑调整算法实现投影仪的高精度标定。采用此方法对投影仪单相机系统完成标定之后,测量了标准球以验证精度,实验表明投影仪单相机系统的平均重投影误差为0.04像素,测得标准球直径平均偏差小于0.1 mm,球心距偏差小于0.05 mm。结果证明,所提出的投影仪标定方法计算模型简单、稳定性高并具有较高的精度,适用于主点偏差较大和投影仪焦距未知的情况。
结构光测量;投影仪标定;平面模型;全参数
随着机器视觉技术的广泛应用,对相机及投影仪的标定精度提出了更高的要求。在现有的结构光测量系统中,单相机-单投影仪组成的结构光三维测量系统,由于具有结构简单、点云重建效率高等优点而具有巨大的应用前景,因此迫切需要提出一种投影仪的高精度标定方法[1-2]。
投影仪自身不能采集图像,也就不能检测标志的坐标信息,目前多采用虚拟摄像机反向成像原理进行标定。其中,利用已标定的相机对投影仪进行标定的方法因原理简单、易于实现,应用最为广泛,但这种方法会引入相机的标定误差。张勇斌等人将投影图案预先进行单应性射影变换,再移动靶标图像使之与投影图像重合的方法,实现投影仪标定,但存在单应性矩阵难以预先获取的问题[3]。韦争亮通过投射双方向相移图案的方法,实现了投影仪与单平面标定块的虚拟成像,用Tsai两步法及非线性优化实现了投影仪的标定[4-5]。Wieghardt利用手眼标定法对手持投影仪进行了标定[6-7]。这些投影仪在进行标定时,均采用成熟的相机标定方法,投影仪本身存在梯度校正,其镜头的轴与芯片点交汇点距离芯片中心很远,使其内参数中主点偏差非常大;并且,当使用短焦、广角或球面镜头,或者当光轴与感光芯片中心的偏移或夹角过大时,图像边缘畸变非常大,主点偏差也跟初值差距甚大,使常规相机标定方法产生标定精度低、计算不稳定的状况。
针对投影仪标定精度较低的现状,国内外学者进行了大量研究。李中伟对投影的光栅图像中非正弦化引起的相位误差进行补偿,提高了投影仪的标定精度[8]。Zhang采用多频相移的方法得到了投影仪的虚拟成像,采用张正友标定法得到投影仪参数[9]。高治华、Liu根据射影变换原理建立投影仪图像和摄像机图像的基本对应关系,利用多项式拟合并进行补偿的方法实现了投影仪的高精度单平面标定[10-11]。Resch提出一个新的半自动投影相机系统的标定方法,根据已知的几何尺寸约束调整,优化结构光投影图像,改善标定的内外参数[12-13]。但是,这些误差补偿方法不能提高计算的稳定性,且耗费较大的计算代价,急需简单高效的实现高精度投影仪参数标定。
本文提出一种平面化模型,利用外差式多频相移技术进行投影,将相位匹配技术与仿射变换关系相结合,得到稳定的直接参数预估算法,便于获取精确的参数初值确保迭代计算的收敛性,然后采用一种全局捆绑调整算法,求得投影仪的内外参数,实现投影仪的高精度标定。
1 基本原理
1.1 投影仪模型
投影仪与照相机在结构上基本相似,可采用小孔成像模型进行分析,投影仪模型如图1所示。
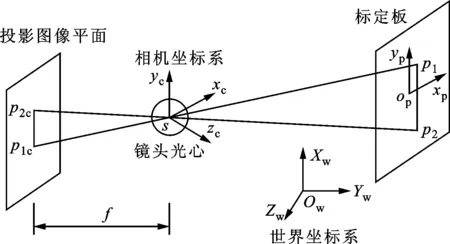
图1 投影仪模型
考虑到干扰因素的存在,像点在成像平面上与其理论值存在偏差,即主点在像平面的偏差,可建立如下共线方程
(1)
式中:ai、bi、zi(i=1,2,3)为旋转矩阵的分量;(Xw,Yw,Zw)为物体点在世界坐标系的坐标;(xc,yc,zc)为投影中心点在世界坐标系的坐标;(x,y)为图像点坐标;(cx,cy)为主点偏差;f为焦距;(Δx,Δy)为镜头畸变引起的像点偏差。
本文采用的畸变模型包括径向畸变、偏心畸变、像平面畸变,即
(2)
令K1、K2、K3表示径向畸变参数,B1、B2表示偏心畸变参数,E1、E2表示像平面畸变参数,则有
(3)
1.2 检测原理
本文采用外差式多频相移技术,利用自主研制的XTOM型三维光学密集点云测量系统[14]实现了投影仪的高精度标定。这种多频相移技术是通过投射多种不同空间频率的条纹,利用相移法求取多种条纹的相位主值,进而得到条纹的真实相位。此方法的解包裹过程对单点独立计算,不存在误差的传递,比单光栅(格雷码加相移法)的相移测量精度更高。
投影仪标定时的虚拟图像获取过程如下:
(1)利用投影仪投射光栅相移图像到标定板,同时触发相机进行同步采集,得到一系列相移图案;
(2)对所采集到的横向光栅相移图片和纵向光栅相移图片分别进行解相,得到各自的总相位图;
(3)根据总相位图,获取标志点中心所在的横、纵向相位值;
(4)通过求解出的相位值,对投影仪的理想相位图进行差值计算,得到投影仪图像中标志点的虚拟坐标。
这样,就可以确定投影图像与标定板之间的对应关系,得到投影仪标定时的虚拟照片。
2 投影仪全参数解算
投影仪采用普通计算方法时焦距未知或不准确,或由于光线干扰等原因,使对应标记点位置存在误差,而解算内外参数时,须保证所有计算点完全正确,本文通过建立平面化模型,提出一种初值直接预估算法,包括选取最优点集和参数解算,并采用捆绑调整的方法,精确地求解出投影仪的内外参数。
2.1 建立平面化模型
针对投影仪内参数主点偏差非常大、常规方法无法求取的问题,为投影仪的二维坐标点与三维空间坐标点建立一一对应的映射关系,以便简化计算模型。标定板的世界坐标系被对齐到自身平面,该面法线方向为Z轴。局部坐标系P和相机坐标系C存在以下关系
C=RcP+Tc
(4)
式中:Rc和Tc为两个坐标系之间的旋转和平移矩阵。
根据本文的平面化模型假设,在相机坐标系下的图像点坐标Z值为0,物体点在局部坐标系P下Z值也为0,即
(5)
可以看出,点(cx,cy)和(px,py)之间仅与(Rc00,Rc01,Rc10,Rc11,Tc00,Tc10)相关,因此可简化式(5)得到如下仿射变换关系
Cp=A2×2Pp+B2×1
(6)
对于图像上的所有点,其像点坐标(cx,cy)与对应的空间坐标(px,py)均满足仿射变化关系,因此只要图像上有3个以上有效点,即可通过最小二乘法求解6个未知数。
2.2 初值直接预估算法
初值估计时图像的畸变不予考虑,可令畸变参数初值为0,在后文捆绑调整时进行解算。结合上文所采用的平面化模型,式(1)可简化为
(7)
也可改写为
(8)
由于式(8)不能采用线性方法直接求解,定义一个参数向量η,使其线性化,即
(9)
采用该向量将共线方程转化为一个线性方程
(10)
式(10)可简化成矩阵形式Aη=B,通过最小二乘法进行求解
η=(ATA)-1ATB
(11)
这样式(10)通过两步即可线性化求解。首先,在图像中选取最优点集,确定矩阵A和B,利用线性方法求解参数η;然后,通过所有图像的η求解相机的内参数和每幅图像的外参数。
2.2.1 最优点集选取 由于式(8)包含有8个未知数,因此标定图像中必须存在4个及以上的物体点,并可正确识别,即可通过最小二乘方法进行求解。
利用该仿射变换关系即可在所有备选关联点中找出最优点集,提高标定初值的稳定性和精度,具体的步骤如图2所示。首先在所有备选点中按照一定顺序选择5个非共线图像点,初步计算仿射变换矩阵,如果计算失败,或者解算出满足该仿射变换矩阵的点数小于3,则重新选点;然后,对图像中所有点进行判断,选出满足该变换矩阵的点,再重新计算仿射变换矩阵,如果最终有60%以上的图像点满足新的变换矩阵,则这些图像点为有效关联点,即选取的最优点集;最后,使用最优点集计算参数向量η。
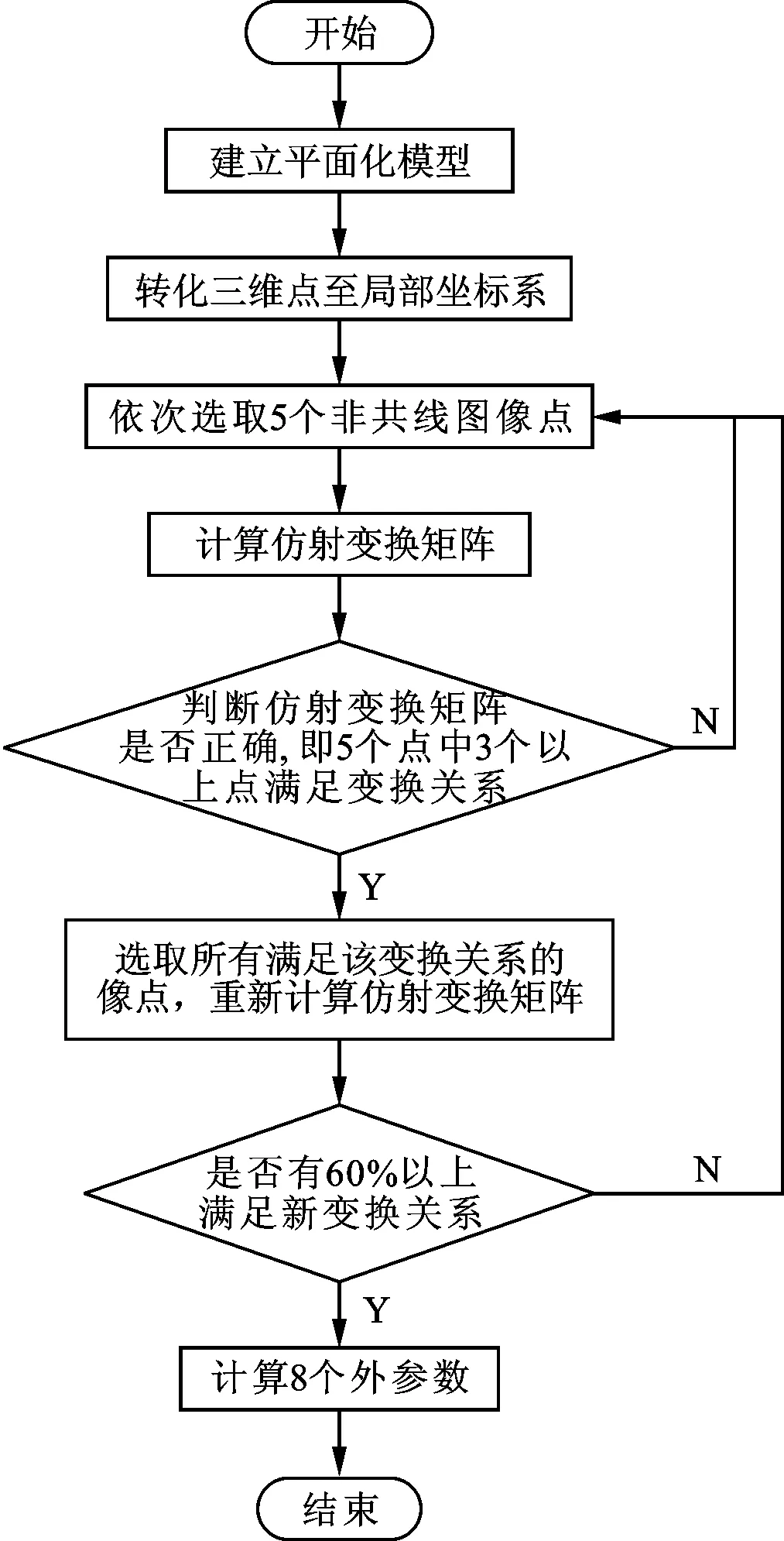
图2 最优点集的获取和外参数计算步骤
2.2.2 预估内外参数 在每一幅图像中存在3个内参未知数(cx,cy,f)和6个外参未知数(ω,φ,κ,tx,ty,tz),当参数组η可以成功求解后,需要进一步处理才能获得相机的这些内参数。
假设ηi在每一幅图像上已知,可推导出一种参数分离算法。因为矩阵R为标准正交阵,故获得了如下线性方程
Cξ=D
(12)
式中
C=
式(12)也可通过最小二乘的方法进行求解,因方程中有4个未知数,因此至少两幅图像才可求解。当ξ获得后,可反解出相机的内参数
(13)
最后,可根据式(14)、(15)计算每一幅图像的外参数。平移矩阵T的计算公式为
(14)
式中
g=(η3-η7cx)2+(η4-η8cx)2+(η5-η7cy)2+
(η6-η8cy)2
旋转矩阵R的计算公式为
(15)
由于上面的计算没有保证旋转矩阵的正交性,因此需要对结果进行正交化处理。对上式获得的R进行SVD分解,获得新的旋转矩阵
R=UVT
(16)
2.3 捆绑调整解算投影仪参数
预估投影仪的内参数和图像的外参数后,由于三维点坐标已知,即可进行全局捆绑调整,该误差方程为
V=AX1+BX2+CX3-L
(17)
式中:X1、X2、X3为内方位参数、外方位参数、物体点三维坐标的改正数;A、B、C为内方位参数、外方位参数、物体点坐标对应的偏导数矩阵;L为观测的真实值与初值偏差。
为了保证稳定性,本文根据前面预估的内外参数初值,采用全局捆绑调整法进行优化,流程如图3所示,共分3步进行:首先,将相机、投影仪内参数和三维点坐标固定,仅调整图像的外参数;其次,将图像的外参数和三维点坐标固定,仅调整相机、投影仪内参数;最后,将三维点坐标固定,同时调整相机、投影仪内参数和每幅图像的外参数。
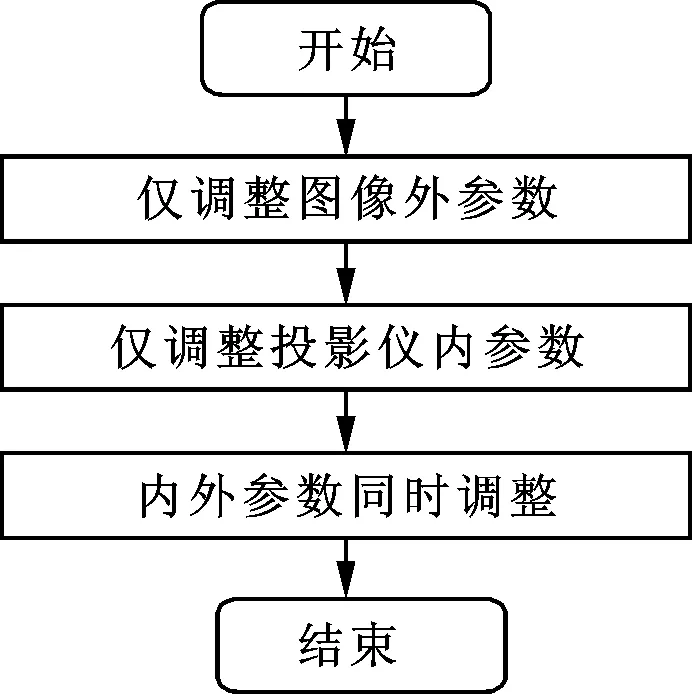
图3 全局捆绑调整法步骤
3 实验及结果
本实验采用自研的XTOM光学面扫描系统进行测试,实验环境如图4所示。

图4 实验环境
3.1 投影仪标定
投影仪标定时焦距未知、主点偏差较大。采用上文所述外差式多频相移技术对投影仪单相机系统进行标定。摄像机型号为Basler,分辨率为1 624×1 236,芯片像元大小为4.4 μm,镜头焦距为16 mm。投影仪位于相机右侧约100 mm处,该数字DLP投影仪型号为DELL,分辨率为1 024×768,像元大小为7.6 μm,焦距未知。标定板位于投影仪正前方约450 mm处,测量幅面为200 mm×150 mm。
标定过程:按1.2节的图形采集过程,从8个不同的方向采集数据,每次采集横向相移、纵向相移各12张图片,共得到192张图片;相机采集图片后对标志点进行了检测,如图5a所示,对多频相移图片进行解相后,可以得到投影仪的虚拟成像,并对标志点进行了检测,如图5b所示。标定过程的整体解算时间为5 s(不包括标志点检测和投影仪虚拟成像的时间)。

(a)相机图像 (b)投影仪虚拟图像图5 标定图像及标志点检测结果
根据文中所述的标定方法,得出相机和投影仪内参数和外参数结果分别如表1、2所示。
通过本次标定实验,计算出了投影仪的焦距,可以看出,投影仪的主点偏差非常大,约400像素,常规方法无法求解。
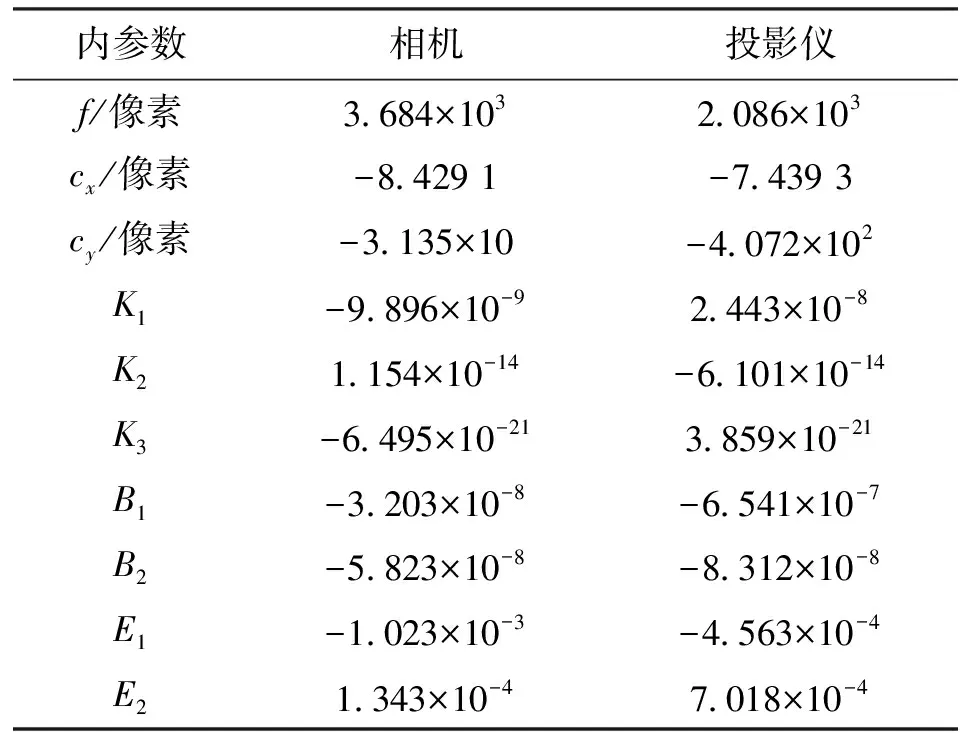
表1 相机和投影标定内参数结果
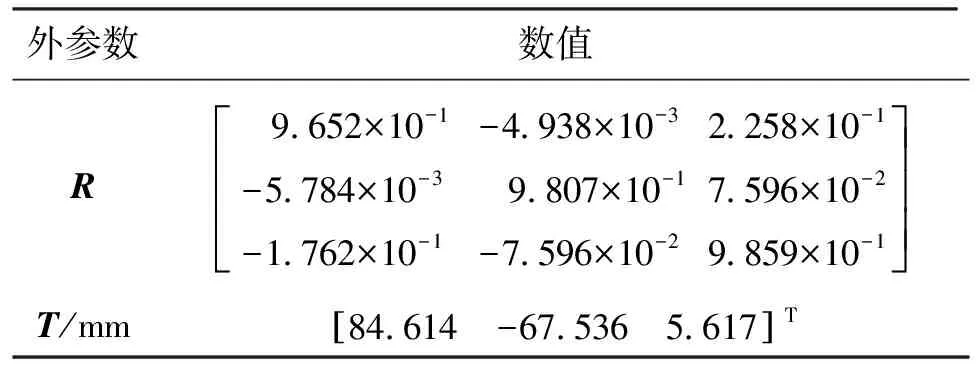
表2 相机和投影标定外参数结果
对于任意的点P(x,y,z),利用标定的相机内外参数,可以根据共线方程计算得到一幅图像上理想的投影点(xp,yp),这样就能得到其与真实像点(x,y)的误差,即反向重投影误差
e=((x-xp)2+(y-yp)2)1/2
(18)
对标定中所有的图像点取重投影误差的平均值,可得到平均重投影误差,值越小说明相机内外参数对图像点和相机模型的描述越准确,即标定结果准确可靠。本次实验标定的重投影误差如图6所示,平均重投影误差为0.04像素,且本标定方法具有较强的通用性,无须针对每个标定平面的结果进行曲线或曲面拟合,计算量小。
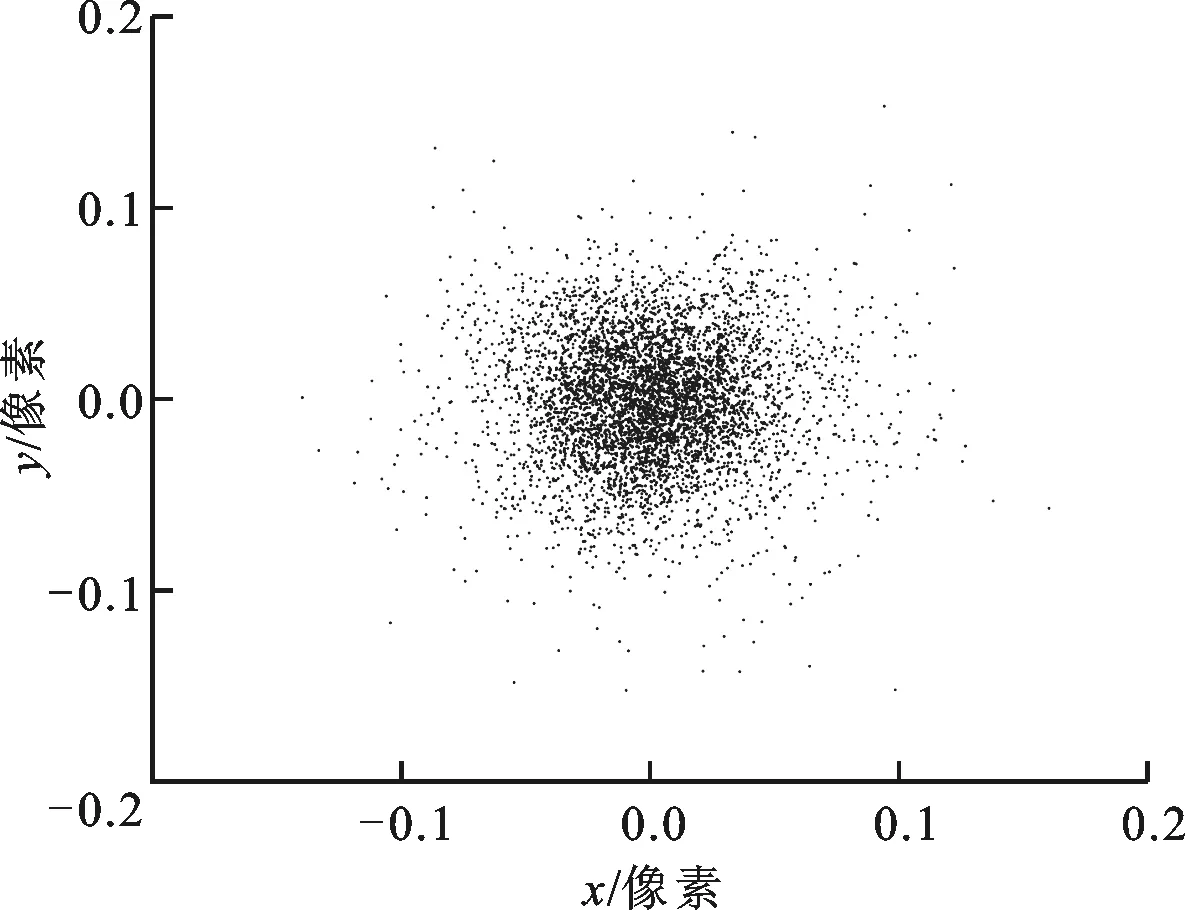
图6 反向重投影误差
3.2 精度验证
采用标准球实验对投影仪的标定精度进行验证,如图7所示,这3幅图片分别代表真实的小球实验环境、投影光栅测量过程和测得的小球数据。对标准球进行了3次测量,所得的标准球直径和球心距如表3所示。

(a)实物照片

(b)光栅投影

(c)测量结果图7 标准球实验
由表3可计算得到本次实验测得的直径A和B的偏差为82.8 μm和72.5 μm,球心距的偏差为32.4 μm。这是由于为消除反光的影响,标准球表面喷涂有显影剂,使标准球直径略有增加,而球心距由表面点拟合而来,消除了显影剂的影响,所以测量结果更为准确。
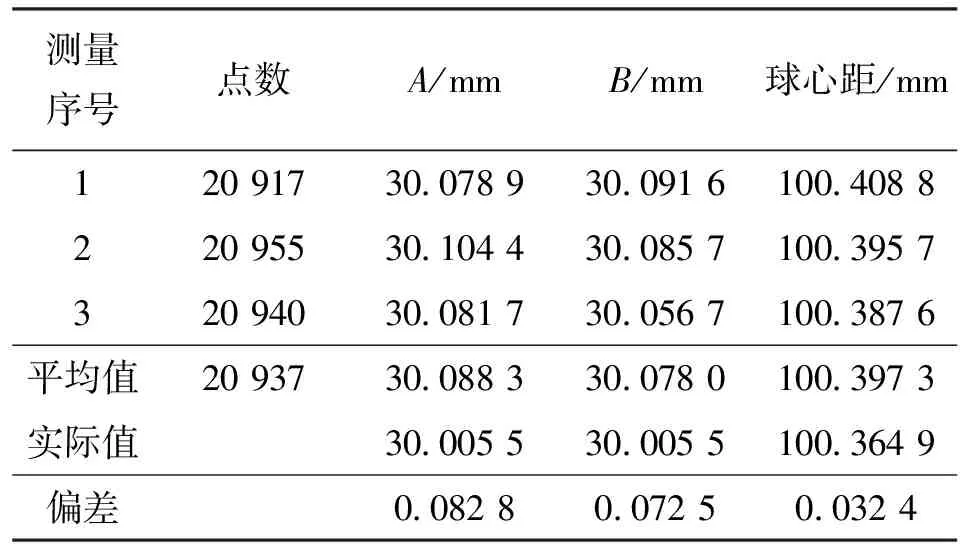
表3 标准球测量数据
4 结 论
(1)文中采用的平面化模型简单,为投影仪的二维坐标点与三维空间坐标点建立了一一对应的映射关系,并在此基础上提出一种直接参数预估算法,能快速获取最优点集,精确地计算出投影仪的参数初值。
(2)本文提出的投影仪标定算法适用于主点偏差较大和投影仪焦距未知的情况,无需预先确定投影仪的主点偏差、焦距等内参数,标定算法通用性较强,无需曲线曲面拟合。
(3)本文根据获取的精确参数初值,采用全局捆绑调整算法,可实现投影仪的高精度标定,平均重投影误差较小。
[1] KE F, XIE J, CHEN Y. A flexible and high precision calibration method for the structured light vision system [J]. Optik-International Journal for Light and Electron Optics, 2016, 127(1): 310-314.
[2] WU H, LI B, ZHANG J, et al. Flexible projector calibration in the structured light 3D measurement system [C]∥Advances in Image and Graphics Technologies. Berlin, Germany: Springer, 2015: 158-166.
[3] 张勇斌, 卢荣胜, 费业泰. 机器视觉中彩色伪随机编码投影系统及标定 [J]. 哈尔滨工业大学学报, 2004, 36(1): 59-62. ZHANG Yongbin, LU Rongsheng, FEI Yetai. Multicolor pseudo-random array pattern projector and its calibration [J]. Journal of Harbin Institute of Technology, 2004, 36(1): 59-62.
[4] 韦争亮, 钟约先, 袁朝龙, 等. 单摄像机单投影仪三维测量系统标定技术 [J]. 清华大学学报(自然科学版), 2009, 49(2): 202-205. WEI Zhengliang, ZHONG Yuexian, YUAN Chaolong, et al. Calibration of a 3D measurement system having one camera and one projector [J]. J Tsinghua Univ (Sci & Tech), 2009, 49(2): 202-205.
[5] 韦争亮, 钟约先, 袁朝龙. 结构光三维测量系统中投影仪标定技术研究 [J]. 光学技术, 2009, 35(2): 256-260. WEI Zhengliang, ZHONG Yuexian, YUAN Chaolong. Research on the calibration technique of projector in structured light 3D measurement system [J]. Optical Technique, 2009, 35(2): 256-260.
[6] WIEGHARDT C S, WAGNER B. Hand-projector self-calibration using structured light [C]∥2014 11th International Conference on Informatics in Control, Automation and Robotics. Piscataway, NJ, USA: IEEE, 2014: 85-91.
[7] WIEGHARDT C S, WAGNER B. Full self-calibration of a hand-mounted projector using structured light [C]∥Informatics in Control, Automation and Robotics. Berlin, Germany: Springer, 2016: 43-58.
[8] 李中伟, 史玉升, 钟凯, 等. 结构光测量技术中的投影仪标定算法 [J]. 光学学报, 2009, 29(11): 3061-3065. LI Zhongwei, SHI Yusheng, ZHONG Kai, et al. Projector calibration algorithm for the structured light measurement technique [J]. Acta Optica Sinica, 2009, 29(11): 3061-3065.
[9] ZHANG Z, CHENG W. Iterative projector calibration using multi-frequency phase-shifting method [C]∥IEEE Conference on Robotics, Automation and Mechatronics. Piscataway, NJ, USA: IEEE, 2015: 1-6.
[10]高治华, 王昭, 黄军辉, 等. 基于射影变换的结构光测量系统中投影仪标定方法 [J]. 中国激光, 2012, 39(10): 160-167. GAO Zhihua, WANG Zhao, HUANG Jianmin, et al. Projector calibration method based on projective transformation for structured light measurement system [J]. Chinese Journal of Lasers, 2012, 39(10): 160-167.
[11]LIU M, SUN C, HUANG S, et al. An accurate projector calibration method based on polynomial distortion representation [J]. Sensors, 2015, 15(10): 26567-26582.
[12]RESCH C, KEITLER P, MENK C, et al. Semi-automatic calibration of a projector-camera system using arbitrary objects with known geometry [C]∥2015 IEEE Virtual Reality. Piscataway, NJ, USA: IEEE, 2015: 271-272.
[13]RESCH C, NAIK H, KEITLER P, et al. On-site semi-automatic calibration and registration of a projector-camera system using arbitrary objects with known geometry [J]. IEEE Transactions on Visualization and Computer Graphics, 2015, 21(11): 1211-1220.
[14]梁晋, 肖振中, 臧顺来, 等. 外差式多频相移技术的三维光学点云测量研究 [J]. 锻压技术, 2008, 33(1): 143-147. LIANG Jin, XIAO Zhenzhong, ZANG Shunlai, et al. Study on 3D optical points dense cloud measuring system based on heterodyne multiple frequency phase shif technology [J]. Forging & Stamping Technology, 2008, 33(1): 143-147.
[本刊相关文献链接]
王昆明,谢建,周召发,等.双轴旋转捷联惯导的误差参数标定方法.2016,50(10):153-160.[doi:10.7652/xjtuxb201610 023]
杨源,库涛,查宇飞,等.快速多特征金字塔的尺度目标跟踪方法.2016,50(10):49-56.[doi:10.7652/xjtuxb201610008]
赵皓,高智勇,高建民,等.一种采用相空间重构的多源数据融合方法.2016,50(8):84-89.[doi:10.7652/xjtuxb2016 08014]
徐张宝,马大为,姚建勇,等.采用干扰估计的液压系统自适应鲁棒控制.2016,50(8):123-129.[doi:10.7652/xjtuxb 201608020]
张平,张小栋,董晓妮,等.滑动轴承润滑油膜厚度光纤动态精密检测模型.2016,50(5):45-50.[doi:10.7652/xjtuxb 201605007]
姚翠萍,周湘连,王晶,等.纳米金标记细胞的荧光寿命成像及其三维重建.2016,50(4):153-158.[doi:10.7652/xjtuxb 201604023]
田红亮,余媛,陈甜敏,等.考虑表面粗糙度和几何曲率的两球体接触问题.2016,50(3):1-7.[doi:10.7652/xjtuxb2016 03001]
朱爱斌,何大勇,邹超,等.刀具磨损图像视差图的非标定方法.2016,50(3):8-15.[doi:10.7652/xjtuxb201603002]
陈江城,张小栋,李睿,等.利用表面肌电信号的下肢动态关节力矩预测模型.2015,49(12):26-33.[doi:10.7652/xjtuxb 201512005]
滕卫军,王锡凡,石文辉.大型风电场动态等值的改进支持向量聚类算法.2015,49(5):94-99.[doi:10.7652/xjtuxb2015 05015]
丁正龙,徐月同,傅建中.深孔内径的在线精密测量原理及系统.2015,49(1):65-71.[doi:10.7652/xjtuxb201501011]
(编辑 荆树蓉)
High-Precision Calibration for Wholly Parametric Plane Linear Estimation Algorithm of Projector
GONG Chunyuan1,2,LIANAG Jin1,2,WEN Guangrui1,2,PAI Wenyan1,2,LI Leigang1,2
(1. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. Guangdong Shunde Xi’an Jiaotong University Academy, Foshan, Guangdong 528300, China)
To solve the problem that the complex optical path of projector and the large deflection of main point are difficult to meet the requirement of high-precision calibration, a wholly parametric plane linear estimation algorithm of the projector was put forward to determine the initial deviation value of main point. Thus, the wholly parametric high precision calibration of the projector can be fulfilled. Firstly, the projector is treated as a virtual camera to obtain the coordinates of the projector and the calibration board through multiple frequency phase shift principle. Secondly, a two-step method is utilized to solve the nonlinear equations. To obtain the stable direct parameter estimation, a vector parameter is introduced to solve the linearization of the nonlinear equation and an optimal point set is selected by affine transformation relationship. Finally, a global bundle adjustment algorithm is developed to implement high precision calibration of the projector. After the calibration of single camera system, the standard balls are measured to verify its accuracy. The experimental results showed that the average value of the projector-camera system’s re-projection error is 0.04 pixel, and the average deviation is less than 0.1 mm in diameter and 0.05 mm in distance acquired by the standard balls. The results further indicate that the algorithm model is simple, stable and accurate. Above all, the projector calibration algorithm can be applied to the situation that the displacement of main point has a large deviation and focal length is unknown.
structured light measurement; projector calibration; plane model; wholly parametric
2016-03-26。 作者简介:龚春园(1989—),女,博士生;梁晋(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51421004,51275378,51275389);中央高校基本科研业务费专项资金资助项目;广东省公益研究与能力建设专项资金资助项目(2014A010104003)。
时间:2016-07-18
10.7652/xjtuxb201611006
TP391
A
0253-987X(2016)11-0036-07
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160718.0910.004.html

